二維弧形一致黏彈性邊界單元適用性問(wèn)題研究

葉 丹，周建庭，尹尚之

(1. 重慶第二師范學(xué)院 旅游與服務(wù)管理學(xué)院，重慶400065； 2. 重慶交通大學(xué) 土木建筑學(xué)院，重慶 400074； 3. 中建五局第三建設(shè)有限公司中南分公司，湖南 長(zhǎng)沙 410000)

0 引 言

在大型結(jié)構(gòu)抗震分析中，半無(wú)限域的截?cái)嗝嫣幚矸绞绞菦Q定土體-結(jié)構(gòu)相互作用計(jì)算精度的關(guān)鍵，且設(shè)置人工邊界條件常用于半無(wú)限域空間模型。J.LYSMER等[1]通過(guò)在截?cái)嗝嫣幉贾米枘幔瓿闪损ば匀斯み吔绲氖┘樱涓拍钋逦⒉僮骱?jiǎn)便，但存在低頻失穩(wěn)和精度不高等缺陷。為克服以上問(wèn)題，劉晶波等[2-3]基于柱面波動(dòng)方程，通過(guò)在邊界處施加彈簧-阻尼器，建立了具有良好彈性恢復(fù)性能的黏彈性人工邊界(VSBE)，克服了低頻失穩(wěn)問(wèn)題，獲得了良好的穩(wěn)定性，目前已在有限元軟件中得到了廣泛應(yīng)用。但是，在解決復(fù)雜二維半無(wú)限域動(dòng)力問(wèn)題時(shí)，由于大部分有限元軟件并沒(méi)有直接施加黏彈性邊界的版塊，研究者需要逐個(gè)進(jìn)行彈簧-阻尼器的計(jì)算和施加，消耗了大量的前處理時(shí)間。

首先，筆者針對(duì)集中黏彈性動(dòng)力人工邊界前處理工作繁瑣、精度不高等問(wèn)題，基于一致黏彈性人工邊界(CVABE)及VSBE的理論[4-5]，提出了一種全新的人工邊界，即二維弧形一致黏彈性邊界單元(2DACVABE)，該單元不僅具有VSBE特性，且單元?jiǎng)偠燃白枘峋仃嚺c普通有限單元類(lèi)似。然后，筆者深入討論了在二維空間內(nèi)2DACVABE模型中的震源頻域、介質(zhì)彈性波速和單元厚度對(duì)分析結(jié)果精度的影響。結(jié)果顯示，2DACVABE能得到較好的精度和穩(wěn)定性，并且其效果同時(shí)受到以上多個(gè)因素的影響。最后，筆者給出2DACVABE的適用范圍，為進(jìn)一步的研究工作提供一定的參考。

1 等效黏彈性人工邊界單元

在二維一致黏彈性人工邊界單元中，推導(dǎo)了模型的總體剛度矩陣〔式(1)〕、阻尼矩陣〔式(2)〕[5]。但是，由于總體剛度和阻尼矩陣版塊在目前大型有限元分析軟件設(shè)置中的缺失，模型無(wú)法模擬真實(shí)總體剛度及阻尼，因此迫切需要開(kāi)發(fā)一種等效于VSBE的普通有限單元。

以往的做法是，在已建立的模型區(qū)域外表面上沿法向延伸一層同類(lèi)型的單元，再固定外單元表面節(jié)點(diǎn)。為使邊界上滿(mǎn)足阻尼與的恢復(fù)力要求，利用矩陣等效原理(圖1)，將單元的一致剛度轉(zhuǎn)化為邊界單元等效剛度矩陣，將阻尼矩陣轉(zhuǎn)化為與邊界單元等效阻尼矩陣。

圖1 一致黏彈性邊界單元

(1)

(2)

式中：KBT為切向剛度；KBN為法向彈簧剛度；CBT為切向阻尼系數(shù)；CBN為法向阻尼系數(shù)。

2 二維弧形一致黏彈性邊界單元

2.1 二維弧形一致黏彈性邊界單元的應(yīng)用

等效的黏彈性邊界單元回避了集中黏彈性邊界設(shè)置中逐個(gè)設(shè)置彈簧-阻尼器的過(guò)程，在保證精度的前提下，簡(jiǎn)便地完成了VSBE的施加過(guò)程。但是以往的研究者在處理半無(wú)限域人工邊界時(shí)，為了簡(jiǎn)化模型，多采用平直的邊界。而在VSBE的推導(dǎo)過(guò)程中，采用的是柱面波假設(shè)，簡(jiǎn)化為平直邊界，明顯不符前提假設(shè)條件及實(shí)際情況，因此筆者提出一種新的黏彈性人工邊界處理方式，即二維弧形一致黏彈性邊界單元(2DACVABE)。

在具體設(shè)置中，首先以散射波源作用點(diǎn)為中心，為使得波源至弧形邊界的距離不變，建立以波源為中心、半徑為R的半圓形邊界有限模型，然后沿邊界法向在已建成的有限元模型的邊界上延伸一層普通單元，固定外層邊界，并通過(guò)計(jì)算賦予合適的材料系數(shù)，以替代原離散化的彈簧-阻尼器。系數(shù)的計(jì)算與設(shè)置見(jiàn)2.2節(jié)，模型如圖2。

圖2 弧形一致黏彈性邊界單元

此方法無(wú)需逐一計(jì)算和布置彈簧-阻尼器，大大簡(jiǎn)化了前處理工作。同時(shí)，因模型半徑為定值，避免了材料特性相關(guān)系數(shù)計(jì)算中近似取值所帶來(lái)的誤差，有效提高了有限元?jiǎng)恿Ψ治龅木取?/p>

2.2 等效剛度與等效阻尼的設(shè)置

在弧形邊界單元的剛度與阻尼單元計(jì)算中，參考等效黏彈性人工邊界單元的思路，使CVABE的剛度矩陣與相對(duì)應(yīng)的弧形邊界單元?jiǎng)偠染仃囅嗟龋⒉捎门c剛度成正比的阻尼矩陣[4]，即：

(3)

由定義可推導(dǎo)邊界單元的等效剪切模量和等效彈性模量，如式(4)；對(duì)阻尼矩陣，為使邊界單元設(shè)置更加簡(jiǎn)便，將等效單元的阻尼比例系數(shù)設(shè)置為兩個(gè)方向系數(shù)的平均值[4],如式(5)：

(4)

(5)

綜上所述，只需定義2DACVABE的材料特性相關(guān)系數(shù)，便可使得在有限元軟件中普通單元的阻尼矩陣、等效剛度與CVABE的阻尼矩陣、剛度相等，便完成2DACVABE的設(shè)置。即邊界處應(yīng)力-應(yīng)變情況等價(jià)于CVABE，新的方法明顯簡(jiǎn)化了黏彈性邊界的設(shè)置過(guò)程，并保證了較高的精度。

3 算 例

3.1 有限元模型建立

筆者在建立弧形邊界單元模型時(shí)，取半徑為50 m 的半圓形近場(chǎng)觀測(cè)區(qū)域，模型周?chē)由煲粚訂挝缓穸葐卧瑢⑼鈱庸?jié)點(diǎn)固定。

選取介質(zhì)密度為2 000 kg/m3、楊氏模量為20 MPa、泊松比為0.3的彈性半無(wú)限域介質(zhì)進(jìn)行研究。考慮介質(zhì)Rayleigh阻尼，其α=0.616，β=0.000 312。2DACVABE的材性系數(shù)參考式(4)和式(5)進(jìn)行計(jì)算。在中心點(diǎn)施加1/2個(gè)頻率為1 Hz的正弦脈沖，并取對(duì)稱(chēng)軸處的表面點(diǎn)A和埋深10 m的點(diǎn)B為觀測(cè)點(diǎn)進(jìn)行觀測(cè)，模型見(jiàn)圖3。為驗(yàn)證2DACVABE的效果，同時(shí)建立固定邊界、黏性邊界、遠(yuǎn)置邊界和集中黏彈性邊界等多組模型進(jìn)行對(duì)比分析。

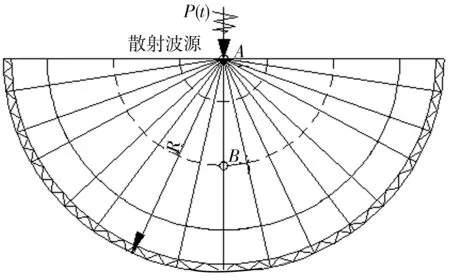
圖3 弧形一致黏彈性單元邊界模型

3.2 弧形一致黏彈性邊界單元精度分析

為驗(yàn)證2DACVABE的精度，對(duì)各邊界模型觀測(cè)點(diǎn)的位移進(jìn)行對(duì)比分析(圖4)，并將建模復(fù)雜、求解效率低但模擬效果最佳的遠(yuǎn)置邊界作為標(biāo)準(zhǔn)解，以尋求精度接近遠(yuǎn)置邊界且建模效率高、求解效率高的人工邊界。

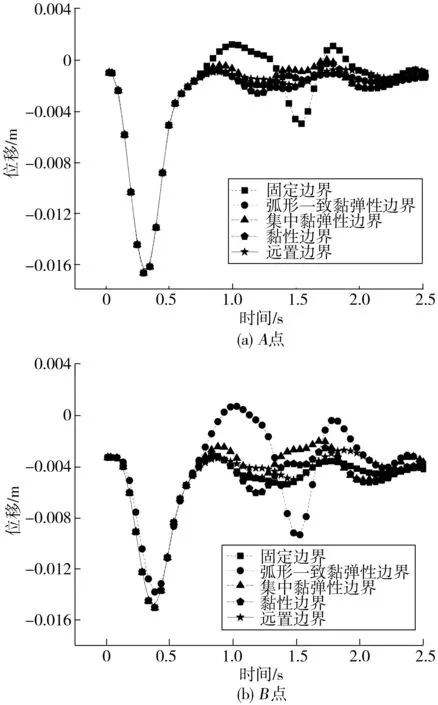
圖4 觀測(cè)點(diǎn)位移時(shí)程曲線

由圖4可見(jiàn)：固定邊界模型出現(xiàn)了明顯的反射干擾現(xiàn)象，與遠(yuǎn)置邊界標(biāo)準(zhǔn)解相差很大，不能反映半無(wú)限域介質(zhì)中波的實(shí)際傳播情況；集中黏彈性邊界模型中，波的反射明顯減少，但在中后段明顯出現(xiàn)了向下漂移情況，筆者認(rèn)為其精度不能滿(mǎn)足要求；黏性邊界、弧形一致黏彈性邊界單元及遠(yuǎn)置邊界模型在脈沖波輸入后，能量迅速減小，僅產(chǎn)生了很小的波動(dòng)，最后幾乎完全被邊界單元吸收，滿(mǎn)足精度要求。將常用的人工邊界與筆者提出的弧形一致黏彈性邊界優(yōu)劣勢(shì)進(jìn)行對(duì)比總結(jié)，如表1。

表1 人工邊界優(yōu)劣勢(shì)對(duì)比

為進(jìn)行人工邊界的精度對(duì)比，將各邊界模型觀測(cè)點(diǎn)位移與遠(yuǎn)置邊界觀測(cè)點(diǎn)位移(標(biāo)準(zhǔn)解)相除，可得表2，并對(duì)表2進(jìn)行處理，得到筆者提出的弧形一致黏彈性邊界與其他常用人工邊界相比后的精度提升系數(shù)，如表3。分析表2、表3可得，弧形一致黏彈性邊界單元模型精度隨著埋深的增加而增加。對(duì)于地表面觀測(cè)點(diǎn)A而言，與其他常用人工邊界相比，弧形一致黏彈性單元的精度提升0.6%～3.4%；對(duì)于埋深較深的觀測(cè)點(diǎn)B而言，與其他常用人工邊界相比，弧形一致黏彈性單元的精度提升3.1%～16.7%;從均值來(lái)看，弧形一致黏彈性單元的精度平均提升3.5%～15.4%。綜上，筆者認(rèn)為，弧形一致黏性單元的計(jì)算精度和穩(wěn)定性均優(yōu)于黏彈性邊界和集中黏彈性邊界，精度與遠(yuǎn)置邊界最為接近，并且其設(shè)置方法更為簡(jiǎn)單，更易于在有限元軟件中實(shí)現(xiàn)。

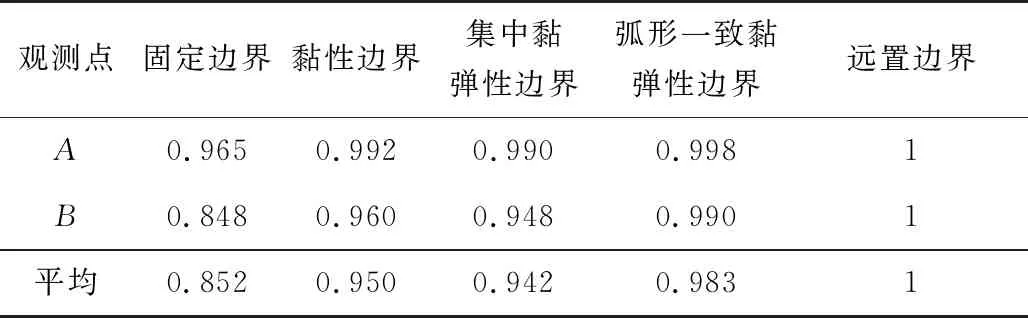
表2 時(shí)程曲線擬合精度對(duì)比

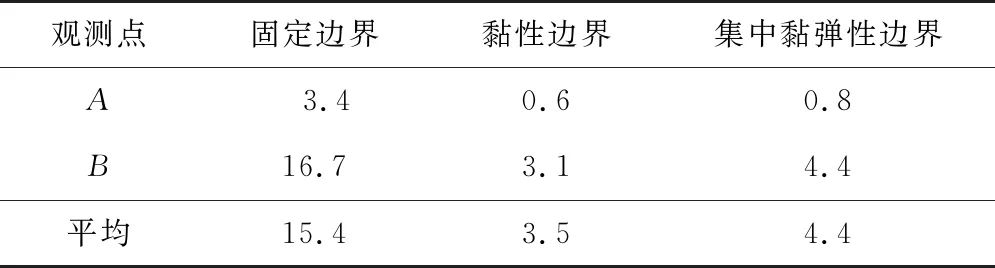
表3 弧形一致黏彈性邊界單元精度提升系數(shù)

3.3 震源頻率與彈性波速

首先，選取多組不同頻率的動(dòng)力荷載進(jìn)行對(duì)比分析，以便于進(jìn)一步研究震源頻率與介質(zhì)彈性波速對(duì)弧形一致黏彈性邊界單元模型的計(jì)算精度影響。各組均為1/2個(gè)等幅值正弦脈沖波，頻率分別為0.35、0.50、1.00 Hz，加載時(shí)程如圖5。然后，在建模過(guò)程中，保持其他因素一致，挑選兩種不同的介質(zhì)彈性波速模型，波速分別為10、100 m/s。通過(guò)對(duì)頻率與彈性波速的多種組合模型進(jìn)行數(shù)值分析，依據(jù)圖6，認(rèn)為介質(zhì)彈性波速和震源荷載頻率均為影響2DACVABE模擬效果精確度的關(guān)鍵因素。

圖5 脈沖波加載時(shí)程曲線

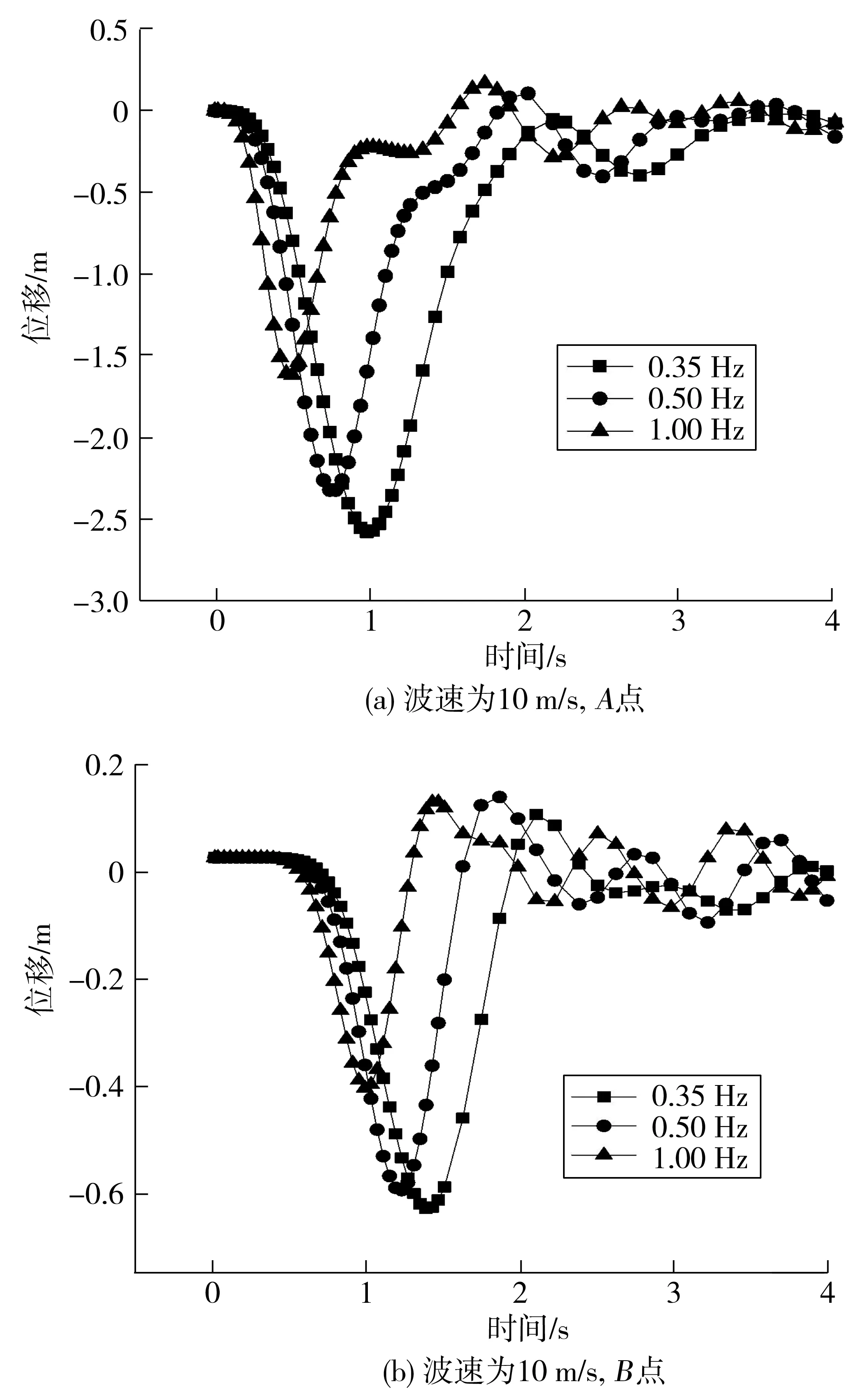
圖6 觀測(cè)點(diǎn)位移時(shí)程曲線

由圖6可知，在保持介質(zhì)彈性波速不變的情況下，震源頻率越高，其后段反射干擾越明顯，模擬效果越差；對(duì)比圖6(a)、圖6(c)或圖6(b)、圖6(d)可知，在相同波源頻率的情況下，模擬效果隨著介質(zhì)彈性波速增大而顯著改善，計(jì)算精度提高。因此，筆者得出震源的頻率和介質(zhì)材料性質(zhì)對(duì)動(dòng)力響應(yīng)均有重要影響的結(jié)論。在有限元軟件計(jì)算中使用2DACVABE時(shí)，建議要合理選擇震源頻率范圍，規(guī)避頻率過(guò)高的震動(dòng)對(duì)結(jié)果的影響，并且要考慮材料性質(zhì)對(duì)模擬效果的影響，對(duì)于介質(zhì)應(yīng)選取較高的彈性波速。

3.4 弧形一致黏彈性邊界單元厚度

在以往的等效黏彈性邊界單元研究中，研究者認(rèn)為，邊界單元的厚度對(duì)模擬結(jié)果影響不大，在1～50倍厚寬比范圍內(nèi)取值均可獲得滿(mǎn)意的結(jié)果[4]。筆者針對(duì)弧形一致黏彈性邊界，選取了厚寬為0.1～5.0的5種模型進(jìn)行計(jì)算，如圖7。

由圖7可知：當(dāng)邊界單元厚寬比h/l≤0.1時(shí)，出現(xiàn)了明顯的反射干擾現(xiàn)象，這主要是因?yàn)閱卧駥挶冗^(guò)小時(shí)，局部位置處可能發(fā)生邊界單元的內(nèi)表面觸及固定外表面的情況，這就解釋了為什么觀測(cè)點(diǎn)時(shí)程圖出現(xiàn)類(lèi)似于固定邊界干擾反射的情況；當(dāng)h/l≥5.0時(shí)，觀測(cè)點(diǎn)出現(xiàn)了明顯的漂移現(xiàn)象，這主要是因?yàn)檫吔鐔卧胶衿湓谙嗤瑧?yīng)力下產(chǎn)生的法向應(yīng)變?cè)酱螅罱K呈現(xiàn)為向下的漂移情況，造成了不可接受的誤差。

圖7 觀測(cè)點(diǎn)位移時(shí)程曲線

綜上所述，通過(guò)計(jì)算不同厚度的人工邊界單元模型的曲線擬合度，發(fā)現(xiàn)弧形一致黏彈性邊界單元厚度對(duì)動(dòng)力響應(yīng)有直接的影響。當(dāng)1.0

4 結(jié) 論

筆者基于弧形一致黏彈性人工邊界及黏彈性人工邊界單元的理論，提出了一種全新的二維弧形一致黏彈性邊界單元概念。具體闡述了該人工邊界的建立思路和在有限元軟件中的實(shí)現(xiàn)方法，并通過(guò)數(shù)值算例分析了其適用性：

1)考慮到集中黏彈性邊界設(shè)置中近似取值所帶來(lái)的誤差和過(guò)于繁瑣的前處理工作，筆者提出了一種新的人工邊界，即二維弧形一致黏彈性邊界單元。該單元模型的操作過(guò)程比集中黏彈性邊界更加簡(jiǎn)單，并通過(guò)算例證明了其具有良好的精度及穩(wěn)定性。

2)人工邊界的動(dòng)力模擬效果與輸入震源的動(dòng)力特性及分析介質(zhì)的彈性常數(shù)存在密切的關(guān)系，建議要合理選擇震源頻率范圍，規(guī)避頻率過(guò)高的震動(dòng)對(duì)結(jié)果的影響，同時(shí)要考慮材料性質(zhì)對(duì)于模擬效果的影響，盡量選取較高的介質(zhì)彈性波速。

3)弧形一致黏彈性邊界單元厚度直接影響到模擬的計(jì)算精度水平。當(dāng)厚寬比h/l超過(guò)推薦范圍(1.0,2.0)時(shí)，即可能存在邊界反射干擾或法向漂移等問(wèn)題，使其計(jì)算結(jié)果存在較大誤差甚至錯(cuò)誤，建議合理選擇單元厚度以控制誤差。