基于可拓云模型的礦井通風系統可靠性評價及靈敏度分析

王豪杰，鄭凱歌，王澤陽，薛黎明

(1.中煤科工集團西安研究院有限公司，陜西省西安市，710054;2.中國礦業大學(北京) 能源與礦業學院，北京市海淀區，100083)

礦井通風系統是礦井通風方式、通風方法和通風網絡的總稱。其任務是向井下各用風地點提供新鮮空氣，以保證井下工作人員的生存需要。另外要保證礦井發生災害時，能夠及時控制風向和風量，并配合其他措施防止災害的擴大[1]。由此可見通風系統在煤礦生產過程中有著重要的地位，只有維持通風系統的穩定運轉，才能為井下工作人員的安全和礦井的正常生產提供保障。因此客觀、準確地對礦井通風系統的可靠性進行分析評價不僅是礦井生產的必要任務，也是對不合理的通風系統進行優化的前提工作。

近年來，礦井通風系統可靠性評價問題引起了國內外學者的廣泛關注。現有的關于通風系統可靠性的單一評價方法主要有基于概率統計理論的評價方法[2]、基于模糊數學理論的評價方法[3-4]和基于人工智能算法的評價方法[5]。以上研究成果在一定程度上豐富了我國礦井通風系統評價理論，但依然存在不足之處。例如利用概率統計方法進行分析時，評價結果的準確性對各項指標的基準值有很強的依賴性；基于模糊數學理論的通風體系評價方法在構建各項指標的隸屬度函數時，受主觀因素的影響較大，忽略了評估結果的客觀性；基于人工智能算法的評價方法在處理過程中，需要大量訓練樣本，導致指標數據的獲取成為難題。基于此，我國學者在礦井通風系統綜合評價方面做了大量研究。程健維等[6]利用灰色系統理論中的灰色聚類分析和模糊綜合評價方法，建立了礦井通風系統綜合評價模型，從而對通風系統可靠性做出了定量化的評價；陳開巖等[7]將變權原理引入模糊綜合評價中，建立了多級變權模糊綜合評價模型，使得變權評價結果的各等級隸屬度差別更加明顯，更加符合礦井實際情況；王克等[8]將物元分析理論應用到礦井通風系統評價中，綜合考慮多種衡量條件對評價目標的優劣利弊，利用關聯度信息對通風系統的等級進行可拓識別，取得了滿意的效果。

基于物元理論的評價方法將通風系統評價作為一個確定的數學模型進行處理，沒有考慮系統分級界限的隨機性和模糊性。筆者通過改進層次分析法(AHP法)得到各項指標的主觀權重，利用熵權法得到各項指標的客觀權重，結合博弈論組合原理確定各項指標的綜合權重。在此基礎上引入云模型，將隸屬函數的精確性拓展為具有統計分布的不確定性，再結合可拓學中的物元理論能夠定性、定量分析問題的優點，提出了一種基于可拓云理論與組合賦權的礦井通風系統可靠性評價方法。

1 可拓云理論簡介

1.1 云理論

李德毅院士[9]在研究概念的模糊性與隨機性問題時提出了云理論，該理論可以實現定性概念與定量數值之間的轉換。設X是一個定量論域，X={x}，C是與X對應的定性概念，對于任意的x∈X，若存在有穩定傾向的隨機數y=μA(x)，則稱y為x對A的隸屬度，而y在論域X上的分布稱為隸屬云。一般通過期望Ex、熵En和超熵He等數字特征表征。其中期望值Ex表示隸屬云的分布中心，反應了定性概念的信息中心值；熵En是定性概念的可度量粒度，熵值越大概念越宏觀，刻畫了可以被分級概念所接受的數據樣本范圍的模糊性；超熵He是熵的不確定性度量，反映了云滴的離散程度。通過三者的結合能夠兼顧分級界限的模糊性與隨機性，構成定性與定量間的相互映射，實現分級區間的軟化。其數字特征和隸屬云如圖1所示。

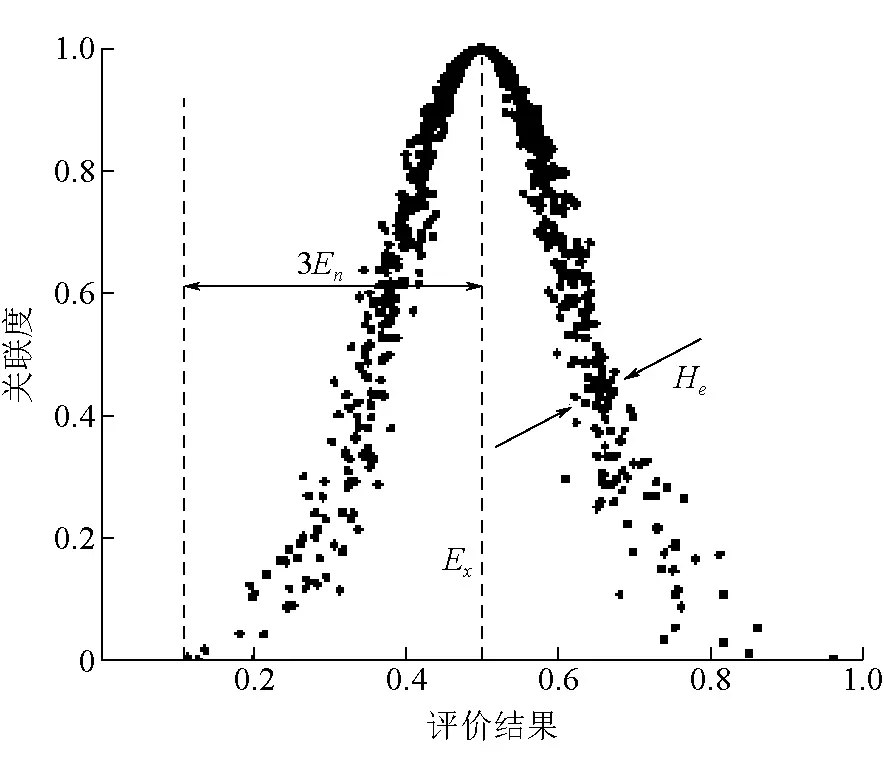
圖1 隸屬云圖

1.2 可拓云理論

蔡文教授在處理矛盾性問題時提出了可拓理論，以物元理論和集合理論為基礎，從定性和定量兩方面處理多指標綜合性評價的不相容問題。將物元概念引入可拓理論中，從而使對象M、特征C和量值V三者相結合，記為：R=(M，C，V)。筆者考慮到云模型具有處理事物的雙重不確定推理特性，利用正態云模型中(Ex，En，He)取代V，從而實現對評估過程中隨機性和模糊性的數學描述。可拓云模型可表示為：

(1)

式中：R——評價等級；

Ci——評價指標；

(Exi，Eni，Hei)——各評價指標對應的云特征數。

可拓云關聯函數的計算類型為數值與標準正態可拓云之間的關聯度模式。首先將待評估的通風系統各項指標因子值x視為一個云滴，并隨機生成服從對應期望值為Ex、標準差為HE的正態分布方差En＇，最后計算出各指標對應的待評估值x與可靠等級界限可拓云模型之間的關聯度k[10]，計算公式為：

(2)

式中：k——關聯度；

x——指標因子；

Ex——期望；

En'——方差。

2 博弈論-可拓云評價模型

運用可拓云模型對礦井通風系統進行評價的過程如圖2所示。

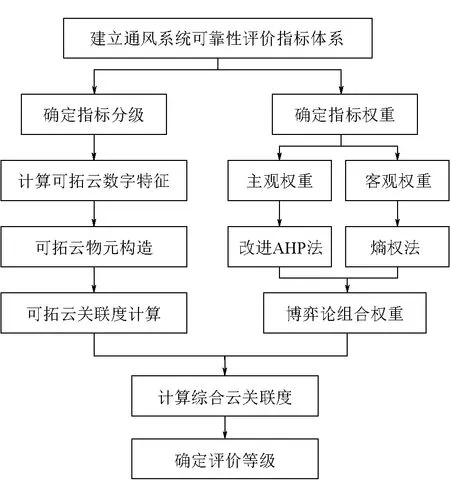
圖2 可拓云模型評價流程

2.1 指標體系的建立

目前對于礦井通風系統是否可靠合理尚未形成明確統一的衡量標準，但是對于評價指標的選取應該遵循科學性、完備性、層次性、可操作性和定性與定量相結合等原則。綜合考慮我國礦井通風系統的實際情況和指標數據的可獲得性，在已有研究成果的基礎上從技術可行、安全可靠和經濟合理3方面建立了由風壓合理性、等積孔和通風機運轉穩定性等16個評價指標構成的礦井通風系統可靠性評價指標體系，并將礦井通風系統的可靠性等級分為可靠、一般和不可靠3個等級，分別用 Ⅰ～Ⅲ 級表示。礦井通風系統可靠性評價指標體系見表1。

由表1可以看出，數值越大，結果越好的指標稱為效益型指標，包括通風機運轉穩定性U11、反風系統合格率U12、防災設施合格率U13、通風設施合格率U14、檢測利用率U16、風壓合理性U21、礦井等級孔U22、用風點風量合格率U24、用風點風質合格率U25、通風方式合理性U26和通風機效率U32等；數值越小，結果越好的指標稱為成本型指標，包括通風網絡復雜程度U15、噸煤通風電耗比U31和外部漏風率U33等；而對于礦井風量供需比U23和用風地點溫度U27兩個指標的量值處于某一區間內結果最佳，所以稱為區間型指標。

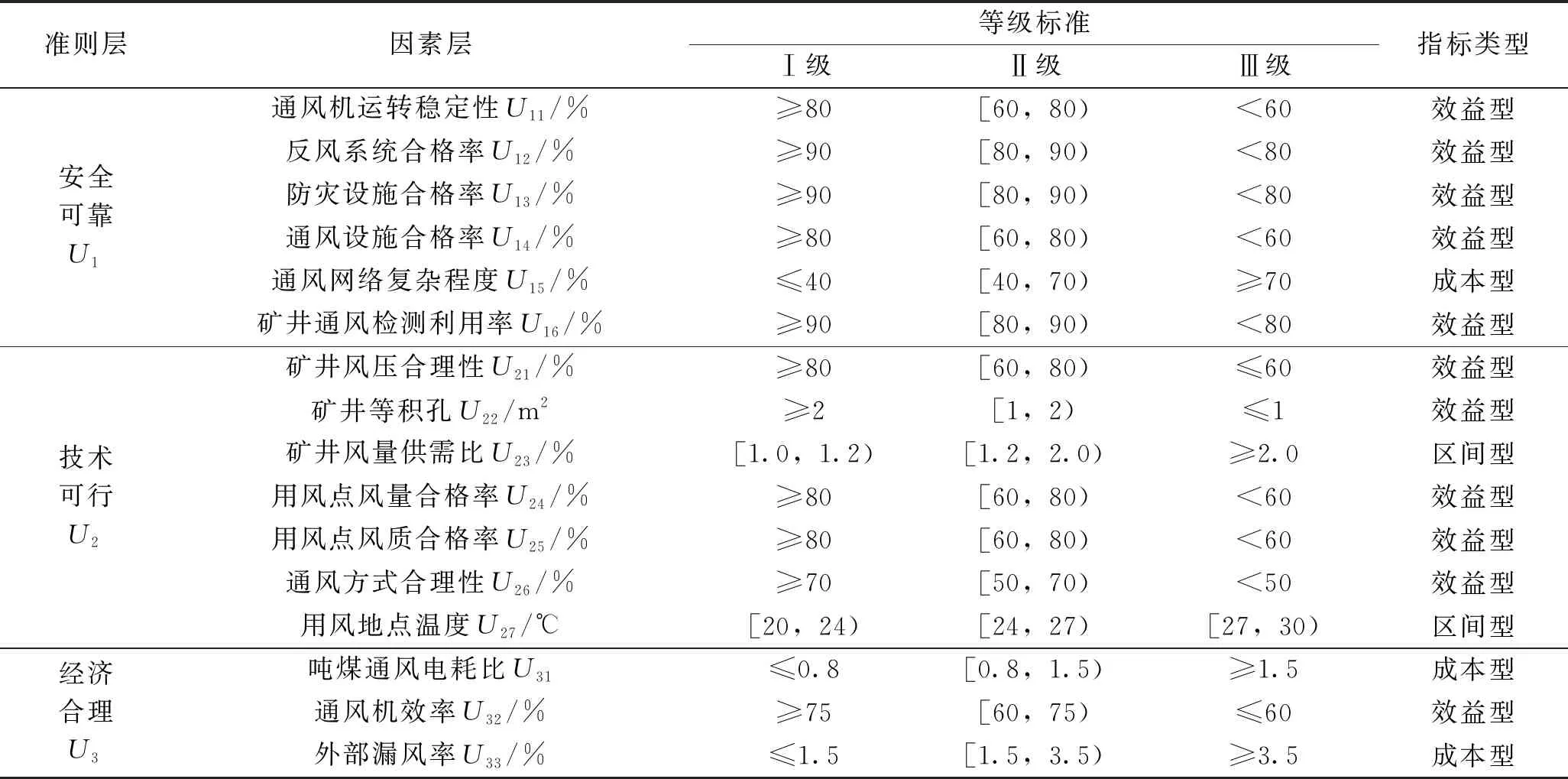
表1 礦井通風系統可靠性評價指標體系

2.2 指標數據標準化處理

為消除指標量綱對評價結果的影響，應對指標數據進行標準化處理。根據上文的指標分類對指標數據進行標準化計算。

(1)對于效益型指標：

(3)

式中：dij——標準化處理后的指標值；

aij——第j個指標的原始值；

ajmin——第j個指標的最小值；

ajmax——第j個指標的最大值。

(2)對于成本型指標：

(4)

(3)對于區間型指標：

(5)

式中：u1j——第j個指標的允許下界；

u2j——第j個指標的允許上界。

2.3 指標權重的確定

為了保證權重分配的合理性，采用主客觀綜合賦權法確定評估指標的權重。其中采用層次分析法確定主觀權重，熵權法確定客觀權重，并采用博弈論組合原理綜合主客觀權重確定指標的綜合權重，該方法不僅有效避免了單一賦權法的缺陷，同時實現了權重分配的主客觀統一，從而保證了各指標權重系數的合理性。

改進層次分析法是一種定性與定量相結合的多目標決策賦權方法。劃分問題的影響因素，形成具有支配關系的層次結構，然后依次比較相鄰變量得出相對重要性排序。具體可參考薛黎明等[11]計算步驟。

熵權法是一種根據各項指標觀測值提供信息量大小來確定指標權數的方法。指標信息量越大，則不確定性越小，對應的熵值也就越小。具體可參考楊力等[12]計算步驟。

博弈論組合賦權法[13]將主、客觀賦權法得到的權重進行優化、融合，從而得到評價指標的綜合權重。具體步驟如下所述。

(1)求n種單一賦權方法的線性組合：

(6)

式中：wk——基本權重向量；

ak——不同賦權方法的線性組合系數。

(2)對線性組合進行優化，使w與wk的離差極小化，求出組合系數ak：

(3)歸一化處理，得到組合權重：

式中：a*——不同賦權方法經優化后的線性組合系數；

w*——博弈論組合權重。

2.4 評價等級的確定

將礦井通風系統評價指標分級界定為雙約束空間，通過各指標區間值和式(11)～(13)計算出指標等級可拓云模型的數字特征：期望Ex、熵En和超熵He。各指標數字特征結果如表2所示。

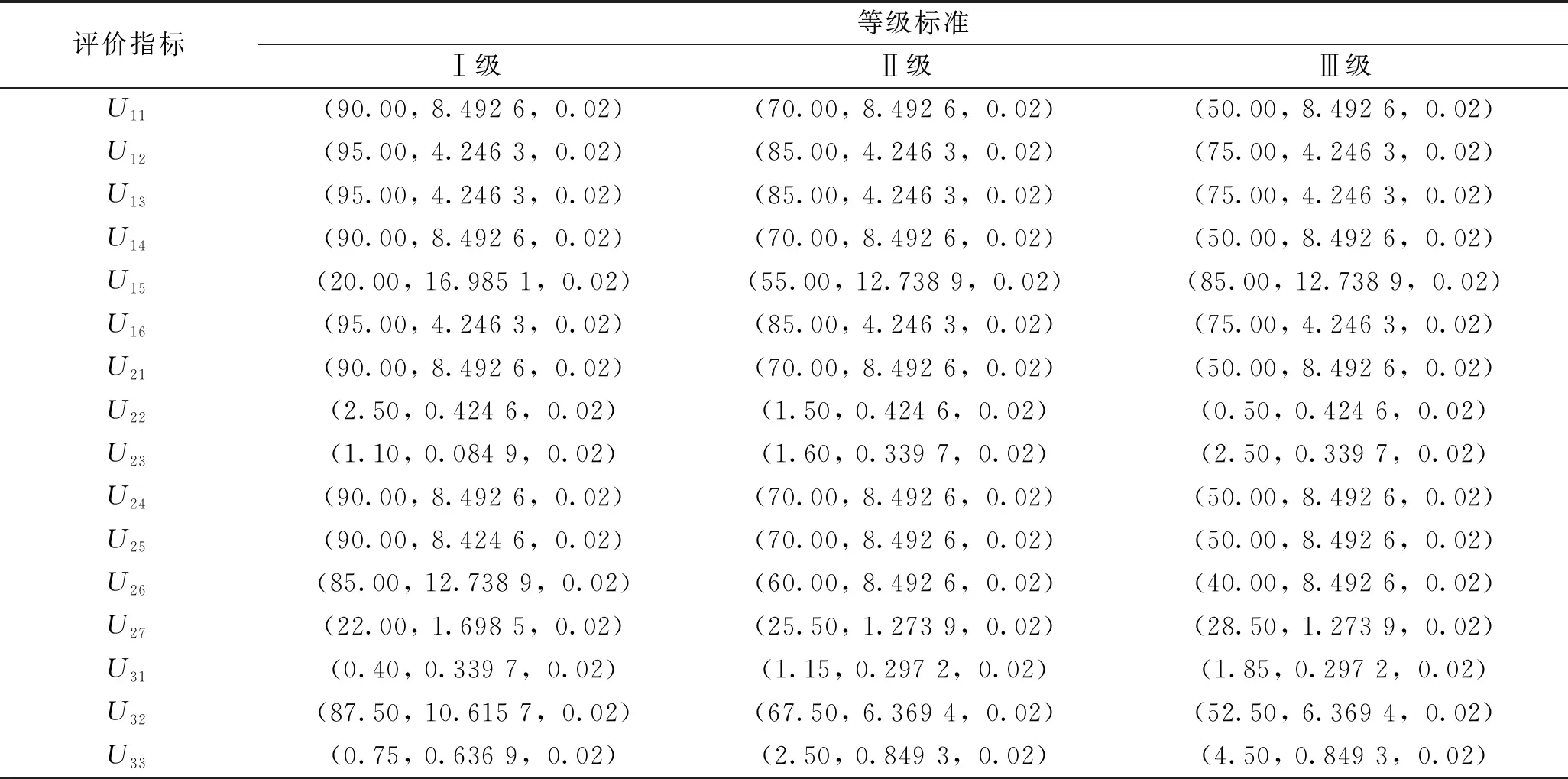
表2 可拓云模型數字特征

式中：Ex——期望；

En——熵；

He——超熵；

xij1——等級標準區間的最小值；

xij2——等級標準區間的最大值。

式中s可結合相應指標的模糊性和隨機性進行調整，本文取0.02。

結合各指標等級云模型的數字特征和式(1)求得評價目標與第j級的第i個指標的云關聯度kij(i=1，2…，16；j=1，2…，5)，令：

(14)

式中：Ph——云關聯度的分布密度值；

wi——綜合權重對應的分量。

結合熵理論和云關聯系數，定義云熵為：

(15)

根據熵理論可知，當待評估樣本的云熵最大時，表明待評估樣本對相應電能質量等級的標準隸屬云的影響最均衡，最大云熵對應的電能質量等級最能體現待評估樣本的性質。

通過式(1)計算出各項指標關聯度，得出綜合評判矩陣Z，結合權重矩陣W得出評判向量B=WZ。利用加權平均法得出綜合評判分數r為：

(16)

式中：bi——向量B的分量；

fi——第i等級的量值。

由式(16)可知，在計算云關聯度的過程中存在隨機因素，因此本文在運行100次后得出綜合評判值的期望Erx和熵Ern。

期望值最能夠代表通風系統可靠性等級的評估值；熵是對評估結果離散度的衡量，熵值越大評判結果越分散。定義可信度因子θ為：

(19)

可信度因子θ值越大表示評價結果離散度越大，結果的可信度越小，反之結果的可信度越大。

3 靈敏度分析方法

靈敏度分析是根據礦井通風系統評價結果的優劣對系統進行優化的一種方法。通過靈敏度分析，可以得出每個指標對評價結果的影響程度，從而確定各指標優化的先后順序，進而根據評價結果對個別指標做出調整，在一定的經濟技術條件下得出最好的優化策略。借鑒已有的靈敏度分析思想[13，15]，筆者提出了礦井通風系統可靠性評價結果對指標值變化的靈敏度分析方法。

3.1 邊際指標值

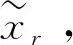
由(20)和(21)相等可得到：

(22)

由云關聯度計算公式(2)可得到：

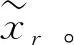
3.2 靈敏度分析

根據計算結果，進行通風系統評價結果對各指標基于邊際指標值的分析如下所述。

根據上述可以得到礦井通風系統可靠性評價等級j、l的綜合云關聯度與指標靈敏度區間如圖3所示。

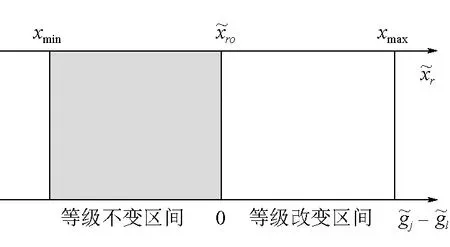
圖3 綜合云關聯度與指標值的靈敏度區間

根據圖3可定義靈敏度區間Δr長度為：

(25)

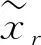
4 實例應用

為了驗證該模型評價結果的準確性，筆者以史秀志等[16]和程剛等[17]8組數據為樣本進行實例分析。結合評價指標和實測數據通過改進AHP法計算主觀權重，熵權法計算客觀權重，基于博弈論原理得出評價指標的組合權重，實測數據和指標權重見表3。

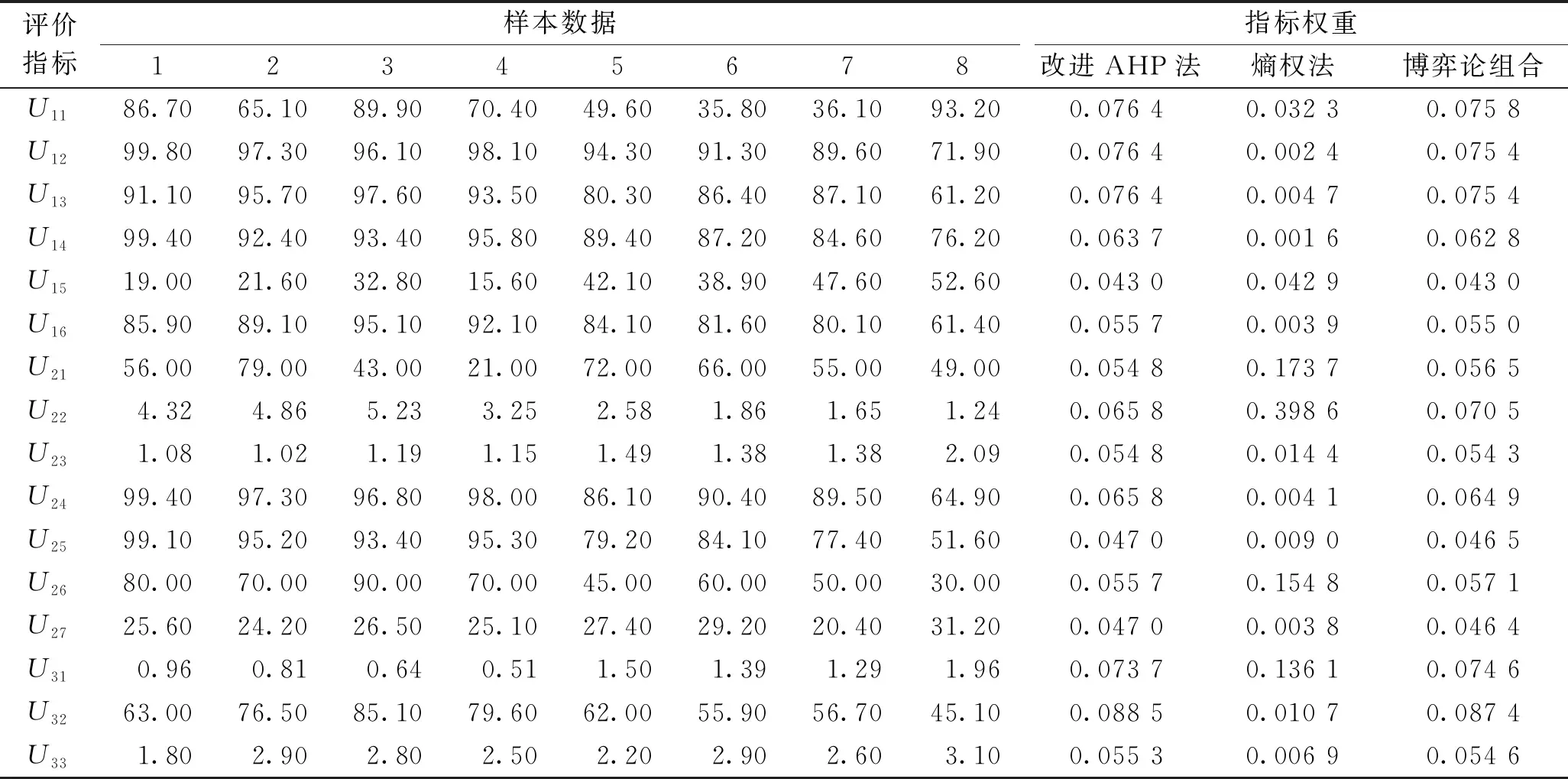
表3 原始數據及其權重

結合樣本1的實測數據和各指標等級云模型數字特征，通過式(1)可以得到各評價指標云隸屬度矩陣Z，再結合權重矩陣W可以分別得到2個樣本通風系統可靠性的綜合云關聯度，對綜合云關聯度進行加權平均可求得綜合評價值Ex。以各指標云隸屬度矩陣為基礎，依據最大確定度原則可求得熵En和超熵He，從而得到樣本1的評價結果數字特征為(1.612 4，0.131 8，0.040 0)。利用正向云發生器可繪制出評價等級云圖，實現結果的可視化，如圖4所示。其中期望表示隸屬云的分布中心，量值大小反應了礦井通風系統的穩定性等級；等級云圖的跨度描繪了礦井通風系統穩定性評價等級的模糊性，跨度越大表明評價等級的模糊性越強；云圖的厚度刻畫了通風系統穩定性評價等級的隨機性，厚度越大表明評價等級的隨機性越強。

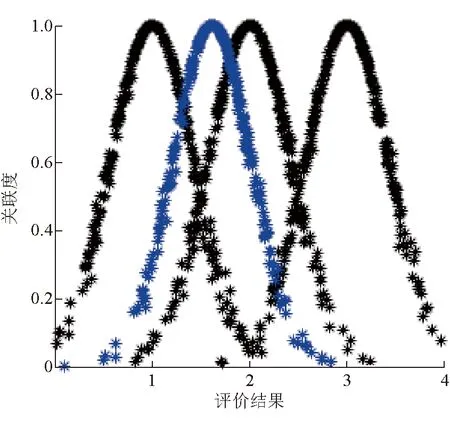
圖4 樣本1評價結果云圖

由圖4分析得出，樣本1礦井通風系統可靠性為Ⅰ～Ⅱ級，通風狀況介于可靠和一般之間。為便于各結果等級可視化對比，分別繪出樣本5和樣本8的評價結果云圖，如圖5、圖6所示。并得到各樣本通風系統可靠性等級。為驗證該模型的準確性，將評價結果分別與ANN模型和FDA模型進行對比，結果見表4。并在各樣本礦井的實際情況基礎上對評價結果進行分析。

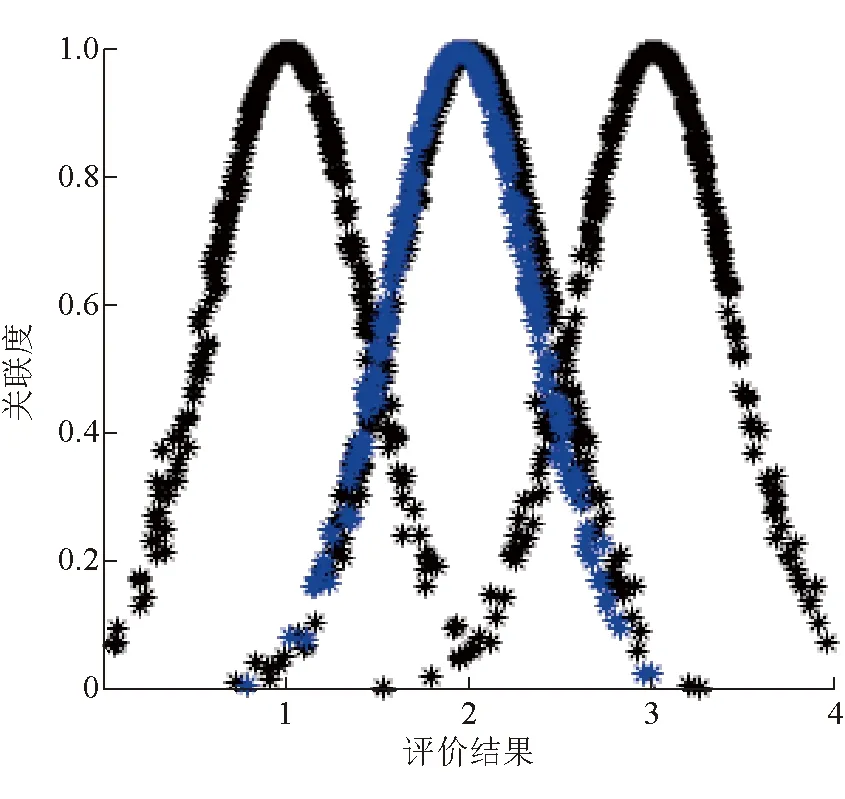
圖5 樣本5評價結果云圖

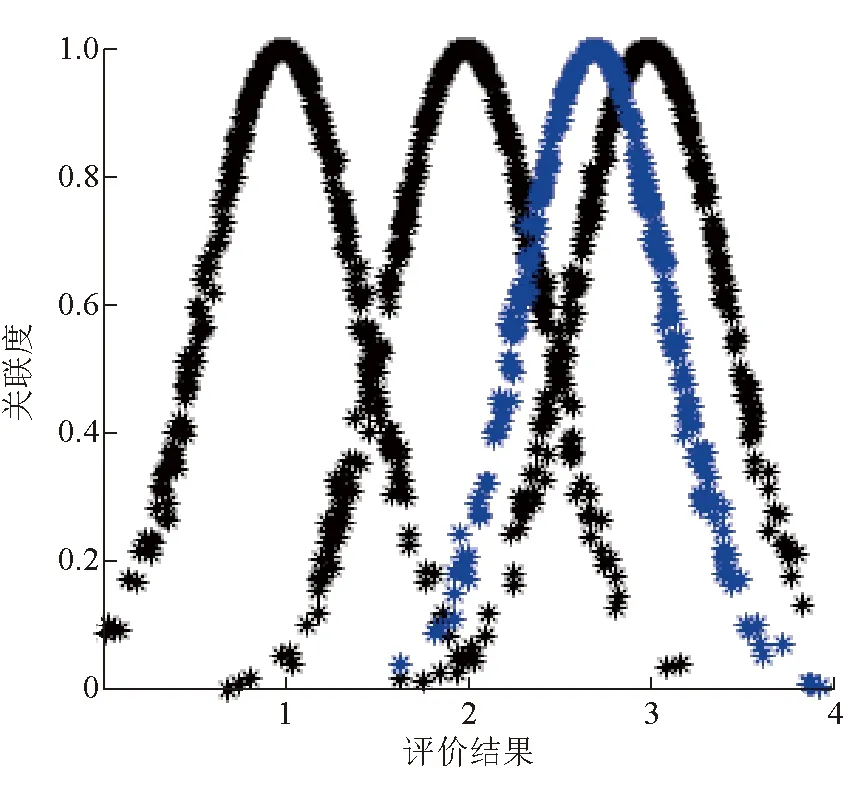
圖6 樣本8評價結果云圖

由表4可知，樣本1與其他模型評估結果有所不同，其他樣本均與其他模型評估結果相同。分析樣本1的實測數據可知指標U11～U15和U22～U26屬于Ⅰ級，指標U16和U27～U33屬于Ⅱ級，而指標U21屬于Ⅲ級，綜合各指標的隸屬等級情況，采用可拓云模型不僅兼顧了系統信息的不確定性，也實現了對等級標準分級的軟化，因此將該樣本礦井通風系統可靠性判定為Ⅰ～Ⅱ級之間更加合理。

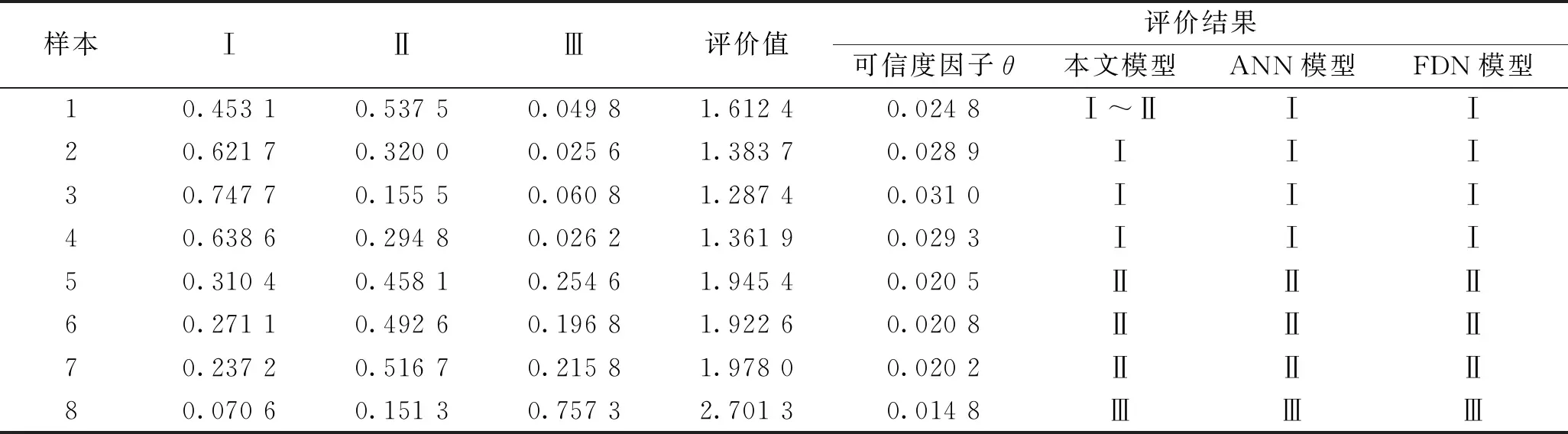
表4 各樣本評價結果

樣本2～4礦井通風系統的可靠性為Ⅰ級，通風系統狀況可靠。這4個樣本礦井中反風系統的靈活性較高，防災設施的質量較好，若發生煤塵燃燒、瓦斯爆炸等災害時，能夠迅速改變風流方向，降低危險程度。另外礦井風量供需合理，既滿足各用風地點的風量和風質要求，又沒有造成風量過量的浪費。在合理布置采掘巷道的基礎上，礦井通風系統較為簡單，礦井通風較為容易，通風系統可靠性較好。

樣本5～7礦井通風系統的可靠性為Ⅱ級，通風系統狀況一般。這3個樣本礦井雖然具有通風設施和反風系統的靈活性較高、通風系統的復雜程度較低和礦井風量比較合理等優點，但是通風機運轉不穩定，存在一定的安全隱患。在經濟因素方面，礦井外部漏風率較高和噸煤通風電耗比較大，導致通風系統狀況一般。另外井下工作面和施工巷道的溫度較高，工人的工作環境較差。以上綜合因素導致這3個礦井的通風系統穩定性為Ⅱ級。

樣本8礦井通風系統的可靠性為Ⅲ級，通風系統狀況不可靠，可能會在礦井實際生產中引發礦井事故，為此對各指標進行分析。由指標原始數據可以得出：通風機運轉穩定性U11、通風設施合格率U14、通風網絡復雜程度U15、礦井等積孔U22、用風點風量合格率U24、外部漏風率U33等6項指標值隸屬于Ⅰ、Ⅱ級，說明這6項指標對應的礦井通風情況較好。其余10項指標值均屬于Ⅲ級，嚴重影響了礦井通風系統的可靠性。因此根據式(20)～(25)計算，這10項指標的邊際指標值和靈敏度區間長度，并進行靈敏度分析，計算結果見表5。

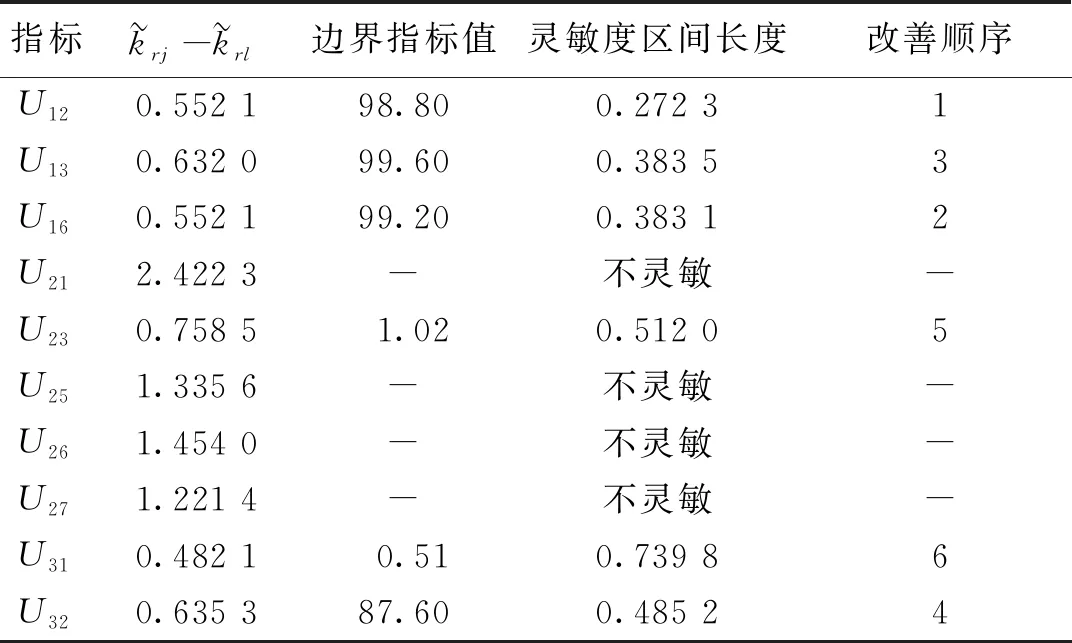
表5 各指標的邊際指標值及靈敏度區間長度

靈敏度區間長度Δr越小，則指標的靈敏度越高，由表5可以看出，指標U12～U32的靈敏度區間長度排序為ΔU21<ΔU16<ΔU13<ΔU32<ΔU23<ΔU31。因此礦井決策人員可以結合礦井的實際情況以這6個指標的靈敏度區間大小排序為依據，對礦井通風系統進行優化。

5 結論

基于博弈論-可拓云模型的礦井通風可靠性評價結果與工程實際相符，并且比傳統評價模型更為精準，為礦井通風可靠性評價提供了一種新的可借鑒方法。

(1)礦井通風系統可靠性評價是一種多屬性復雜問題，筆者基于博弈論組合優化理論將主觀權重與客觀權重相結合得到組合權重，既考慮了主觀意愿的影響，也兼顧了指標值的客觀情況，增強了賦權結果的合理性。

(2)針對目前礦井通風可靠性評價指標分級和評價過程存在隨機性、模糊性和信息不相容性等問題，將云模型的不確定推理特征融入可拓學物元理論中，構建了基于可拓云的礦井通風可靠性綜合評價模型，提高了評價結果的準確性。

(3)將基于指標值的靈敏度分析方法引入到礦井通風系統可靠性評價領域，根據評價結果，分析礦井通風系統綜合評價等級對各指標值變化的靈敏程度，分別得到了各指標的靈敏度變化區間，決策者可根據區間大小為參考依據對礦井通風系統進行優化。