車載跟蹤設備伺服穩定設計

吳德軍，夏 爽

（揚州船用電子儀器研究所，江蘇揚州 225001）

0 引言

跟蹤設備用于實時指示目標空間位置，為火力打擊提供精確坐標［1-2］。某車載打擊系統主要由載車、炮塔和跟蹤設備組成，三者自下而上相互疊加，其中炮塔在載車上能夠進行方位運動，跟蹤設備天線在炮塔上能夠進行方位和俯仰運動。載車在行進中會伴隨橫向縱向搖擺和轉向運動，火炮在使用中會伴隨炮塔轉動，這些都會對跟蹤設備造成干擾，導致跟蹤誤差增大甚至目標丟失。為了能夠在行進中完成對目標的持續跟蹤和火力打擊，就需設計一種跟蹤設備伺服系統，使其能夠隔絕載車行進中姿態變化和炮塔調轉帶來的影響，使跟蹤瞄準線在慣性空間上保持穩定。

常用的慣性空間穩定方法一般有兩種：一種是搭建一個慣性穩定平臺［3-4］，將跟蹤設備置于穩定平臺上，使其在慣性空間上與載車解耦，這種方法將克服擾動問題完全交由穩定平臺解決，早期使用較多，此方案成本高、結構復雜且系統可靠性低，很難滿足車載平臺安裝空間要求；另一種是通過對車和炮姿態角度和速度的檢測［5-6］，結合不同坐標系推導計算，控制跟蹤設備伺服系統的方位和俯仰軸運動，最終使跟蹤瞄準線在慣性空間上保持穩定，這種方法充分利用原有跟蹤設備的方位俯仰伺服機構［7］，結構簡單成本低，且伺服系統響應能力也相對較高，但是需要解決伺服穩定設計的問題，綜合考慮采用此種方法。

1 伺服穩定分析

1.1 載車坐標系定義

要實現穩定跟蹤，準確的車體姿態數據必不可少，所有的穩定跟蹤都是建立在可靠的測量數據之上。在設計中采用光學慣性導航設備對姿態進行測量，可以連續輸出車輛的航行角、俯仰角和側傾角。

天線和炮塔組合體安裝在載車上，而慣性導航設備敏感的是大地坐標系下的數據，所以在穩定分析中首先應當對姿態數據進行大地坐標系（n系）和載車坐標系（c 系）解算。兩坐標系轉換示意圖如圖1 所示。如圖所示，大地坐標系由OXnYnZn表示，原點位于車體搖擺中心O，其中OXn指向正東位置，OYn指向正北，OZn垂直于大地向上［8-9］。載車坐標系由OXcYcZc表示，其中OYc表示車首方向，也是車輛正向行駛方向，OXc垂直于車首方向且指向其右側，OZc指向車輛上方，和其他兩個方向垂直。

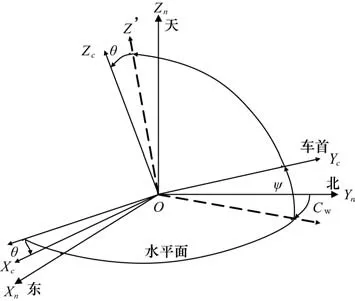
圖1 大地坐標系和載體坐標系

根據歐拉定理，剛體繞固定點轉動可以是繞該點的若干次轉動的合成，載體坐標系就是由大地坐標系經過3 次轉動得到，轉動順序依次是圍繞Z 軸-X 軸-Y 軸。使用航行角、俯仰角和側傾角來表示轉動的角度：Cw 為航行角，正北方向和車首OYc到水平面的投影的夾角，順時針方向為正；ψ 為俯仰角，車首OYc和水平面之間的夾角，向上為正；θ 為側傾角，車體圍繞車首OYc旋轉的角度，右側向下為正。

影響跟蹤設備瞄準線穩定的因素除了載車姿態變化還有炮塔調轉帶來的影響。炮塔調轉角度由和炮塔方位軸同軸安裝的自整角機獲取，使用Gw 表示調轉角度，規定從上向下方向，順時針方向為正。

1.2 目標角度計算

要實現目標跟蹤，首先要計算載車坐標系和炮塔坐標系下目標坐標。根據以上分析，載車坐標系就是由大地坐標系經過航行角、俯仰角和側傾角三次轉動得到，所以求取坐標變換矩陣，使兩坐標系滿足以下關系［10］：

根據3次旋轉關系得到3種變換矩陣，將矩陣相乘即得到載車坐標系和大地坐標系變換矩陣：

在大地極坐標系下目標通常以方位角A、俯仰角E、斜距D的方式給出，通過三角函數計算可以得到目標在直角坐標系下坐標：

而在載車坐標系下目標方位角Ac和俯仰角Ec可以用載車直角坐標系表示為：

假設炮塔調轉角度Gw，結合式（1）～（4），計算得到炮塔坐標系下目標的方位角AG和俯仰角EG為：

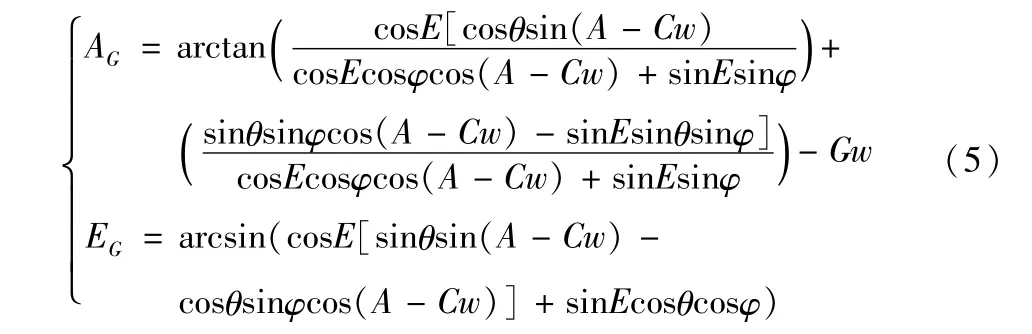
1.3 目標角速度計算

前饋控制是一種重要的伺服控制方法，原理是在伺服控制系統速度環中添加一定的速度補償量，可以有效地改善伺服系統動態跟蹤性能［11-12］。對于跟蹤設備，要減少車體和炮塔運動帶來的附加角速度影響，首先需要計算出外部擾動在方位軸和俯仰軸上的角速度分量，再通過在速度環添加合適的前饋量，抵消外部擾動帶來的影響。

在角速度變換中，可以使用炮塔坐標系作為媒介，先將外界擾動速度轉化為炮塔坐標系三軸角速度，航行角、俯仰角和側傾角以及炮塔旋轉角度在炮塔坐標系下角速度分量分別為：

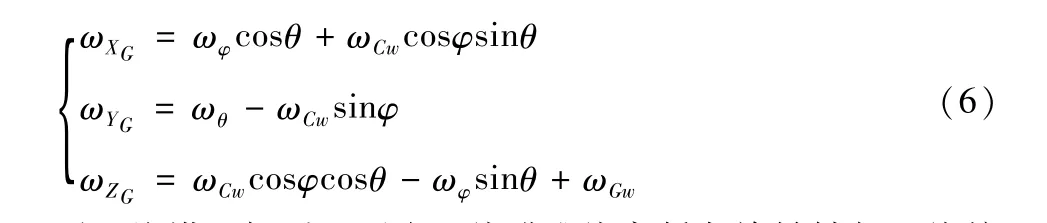
對于炮塔坐標系，因為天線瞄準線高低角旋轉軸與天線俯仰軸一致，故在炮塔水平面內對對瞄準線高低角速度進行分析，炮塔水平面角速度示意圖如圖2所示。

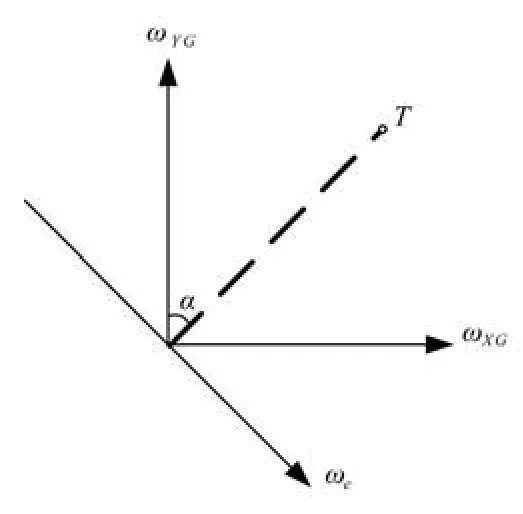
圖2 炮塔水平面角速度示意

假設天線瞄準線角度向上為正，炮塔坐標系下只有XG、YG軸角速度對瞄準線俯仰軸有影響，設天線當前相對于炮塔方位旋轉角度為α，那么車體和炮塔運動在天線俯仰軸的分量為：

已知瞄準線俯仰軸和天線自身俯仰軸一致，為了使瞄準線在俯仰方向保持慣性空間穩定，需要在伺服系統俯仰軸中添加補償量ωec抵消ωe：

對于瞄準線方位角的分析，在OZG和目標T 共存面內進行，如圖3所示。

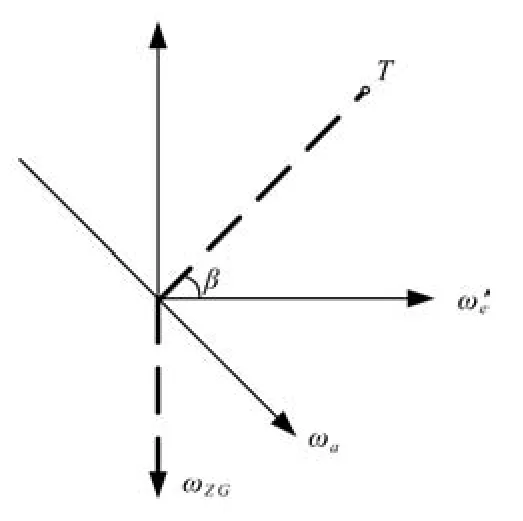
圖3 俯仰面角速度示意

β為當前天線相對于炮塔俯仰角度，ωe′為XGYG在俯仰面的角速度分量的合成量，此分量和ωZG共同合成角速度ωa，可以表示為：

其中：

綜合得到：

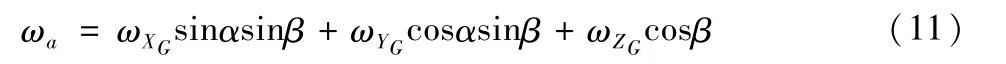
為了使瞄準線在方位方向保持慣性空間穩定，就需要在天線方位軸上增加一個補償速度ωac，能夠抵消ωa對天線影響，即：

計算得到ωac為：

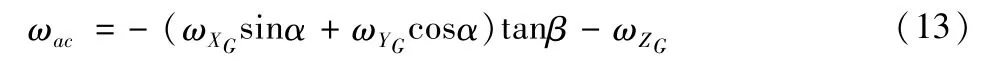
2 伺服穩定系統設計

跟蹤設備伺服控制系統采用電流、速度、位置三環串級控制，系統原理如圖4所示。其中電流環由功率驅動器集成，測速機和旋轉變壓器分別采集電機轉速和天線方位俯仰角度，構成速度環和位置環反饋。車體姿態數據（航行角、俯仰角和側傾角）通過安裝在載車上的慣性導航設備獲得，炮塔轉角由和炮塔共軸安裝的自整角機獲得。位置解算模塊接收大地坐標系下的目標數據，經過計算輸出炮塔坐標系下目標方位角和俯仰角，光纖陀螺用于敏感車體姿態和炮塔角度變化帶來的天線角速度變化，用于伺服系統速度前饋。

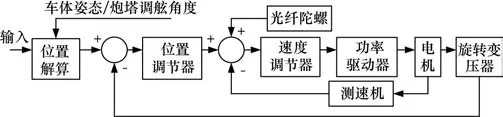
圖4 伺服系統原理

通過以上分析計算得知，車體姿態變換和炮塔旋轉在位置環的反饋角度為AG和EG，在實際中可以通過計算機實時解算獲得。

天線方位俯仰軸的速度前饋量有兩種方法可以獲得：第一種方法是通過對慣性導航設備和炮自整角機輸出的角度進行微分，再通過1.3節的提供的方法進行計算；第二種方法是通過光纖陀螺直接采集相關信號再計算獲得。第一種方法容易引入計算誤差且實時性不足，特別是對于車載設備這種速度角速度變化較大的使用場合，微分得出的角速度往往不準確，故采用第二種方法。

陀螺的安裝位置不同，速度前饋信號的計算方法也不同，基于計算量最小和使用陀螺最少的原則，結合1.3 節對速度前饋的分析，本設計擬采用3個單軸陀螺完成前饋信號采集。陀螺1安裝在天線方位插架上，指向方向和俯仰軸平行，這種安裝方式可以直接敏感出外界擾動在俯仰軸上的角速度分量ωe（圖2）。陀螺2安裝在天線方位基座上，敏感炮塔坐標系Z軸角速度ωZG（圖3），陀螺3 安裝在方位插架的炮塔水平面上，敏感角速度ωe′（圖3）。

已知跟蹤設備的方位軸和俯仰軸是伺服系統控制的兩個旋轉軸，所以在這兩個軸上疊加速度補償量抵消車體姿態變換和炮塔旋轉帶來的速度影響。假設陀螺1、2、3 輸出角速度分別為ωGyro1，ωGyro2和ωGyro3，根據式（8）和式（13），可以得到實際在方位軸和俯仰軸上補償角速度ωac和ωec為：

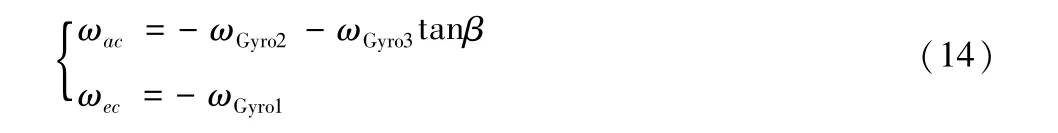
此種安裝方式由于將陀螺直接安裝在需要敏感的軸上，無需復雜的計算和坐標變換就可以直接得到想要的角速度，這種前饋方法不僅計算量小，所帶來的計算誤差也大大減少，并且整個系統的實時性也得到提高。

3 仿真實驗

為了驗證上述伺服穩定控制方法，使用SIMULINK搭建了一個兩軸的伺服控制系統，圖5所示為仿真模型。

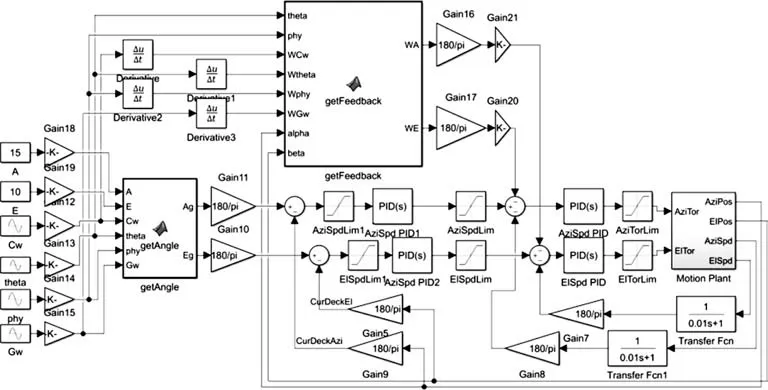
圖5 兩軸伺服控制系統仿真模型

控制系統的輸入包括航行角、俯仰角、側傾角和炮塔方位角以及在大地坐標系下的目標方位俯仰角度，根據1.2節和1.3節的分析，設計模塊getAngle 位置解算單元，將大地坐標系下目標角度轉化為炮塔坐標系下目標角，控制伺服系統完成位置閉環。模塊getFeedback 是前饋量計算單元，用于計算外界擾動對天線方位俯仰軸角速度的影響，輸出前饋控制量。結合實際情況，采用正弦信號作為仿真輸入，仿真參數周期和幅值如表1所示。

表1 仿真設定參數

假設在大地坐標系下目標方位角15°、俯仰角10°，使用同一套控制參數，分別在不加速度前饋和添加前饋情況下進行仿真，得到天線在方位和俯仰方向跟蹤誤差曲線，如圖6～7所示。

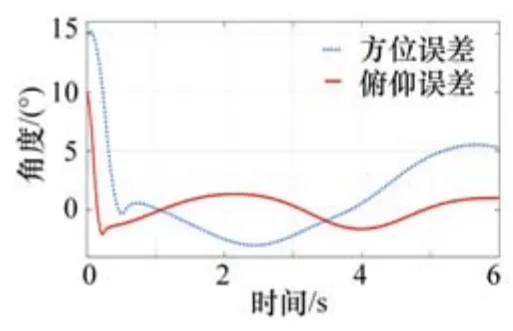
圖6 無前饋下位置誤差

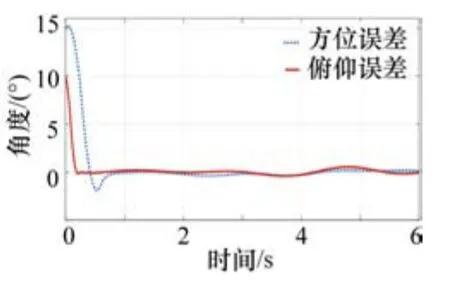
圖7 有前饋下位置誤差

仿真結果表明：（1）添加速度前饋的伺服系統具有更好的跟蹤性能；（2）文中關于角度影響計算和速度影響分析結論準確可靠，伺服穩定系統能夠很好地克服包括航行角、俯仰角、側傾角和炮塔方位角變化帶來的影響。

4 實驗結果與分析

上述仿真測試方法驗證了包括航行角、俯仰角、側傾角和炮塔方位角在內的所有外界擾動對控制系統的影響，但是所用的角速度量是由微分的來的，速度前饋數據為理論計算的結果，并不能驗證陀螺安裝方式的正確性以及實際的控制效果。

為進一步驗證上述控制方法的實際效果以及陀螺速度前饋的可行性，設計了搖擺臺穩定控制實驗。試驗所使用的搖擺臺是一個兩自由度設備，能夠按照正弦變化規律模擬側傾角和俯仰角運動，試驗中設定側傾角幅值10°，周期8 s，俯仰角幅值20°，周期7 s。實測輸出角度如圖8所示。

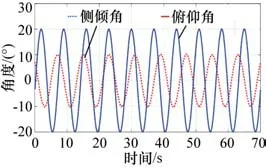
圖8 搖擺臺位置輸出

參照仿真實驗，在不加陀螺速度前饋情況下，天線方位軸和俯仰軸跟蹤誤差如圖9所示。采用相同的控制參數，在添加陀螺速度前饋情況下，天線方位軸和俯仰軸跟蹤誤差如圖10所示。

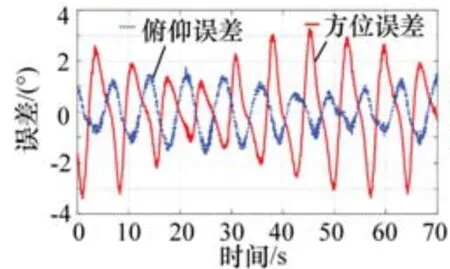
圖9 無前饋下位置誤差

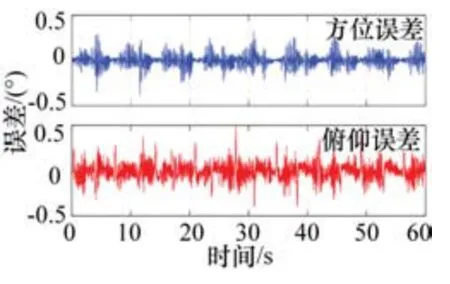
圖10 有前饋下位置誤差

對比圖9和圖10 的誤差輸出結果，可以明顯地看出，基于陀螺速度前饋的伺服穩定系統具有良好的控制效果，陀螺安裝位置正確。

5 結束語

車載跟蹤設備容易受到載車和炮塔運動的影響，造成跟蹤精度降低甚至目標丟失。為了使跟蹤設備能夠克服外界擾動保持連續穩定跟蹤，本文提出了一種帶速度前饋的雙閉環控制系統，并完成擾動量在方位俯仰軸上的角度和角速度分量計算。為進一步提高控制精度，使用陀螺完成角速度采集，基于計算量最小和使用陀螺最少的原則，給出了一種陀螺安裝方式。最后通過模型仿真和搖擺臺實驗，驗證了新的控制方法對包括航行角、俯仰角、側傾角和炮塔方位角在內的所有外界擾動都有很好的隔離作用，陀螺安裝位置有效可靠，控制方法獲得了滿意的效果。