九寨溝MS7.0地震強地震動模擬及參數敏感性分析

李明會 景月嶺,2 張宇璇 鄭司元 宛明晨 何李浩

1 合肥工業大學土木與水利工程學院，合肥市屯溪路193號，230001 2 水沙科學與水利水電工程國家重點實驗室，北京市清華園1號，100089

2017-08-08四川省九寨溝縣發生MS7.0地震。關于九寨溝地震強地面運動數值模擬的研究取得了一些成果[1-4]，但仍有不足之處，如應用復合震源模型進行模擬及其震源參數敏感性分析的研究較少、隨機有限斷層法計算地震動分量方向單一、地震峰值加速度擬合精度不高等。為此，本文應用復合震源模型對九寨溝MS7.0地震強地面運動數值模擬展開研究，并探討不同模型參數對合成地震動的影響規律，為九寨溝地區工程場地地震安全評價提供參考依據。

1 復合震源模型基本理論

復合震源模型是用于計算寬頻帶強地面運動的有限源模型[5]。該模型通過描述震源的運動學特征，結合地震波在層狀介質中的傳播過程，將廣義反射和透射系數法[6]得到的格林函數與震源時間函數進行卷積，計算得到寬頻帶地震動。模型中，強震震源被認為是大量具有恒定應力降圓形子震的疊加。首先將斷層面劃分成一系列尺寸相同的正方形子斷層網格，之后用一定數量和相應半徑大小分布服從Frankel自相似模型[7]的圓形子震填充該斷層面，并允許其部分重疊。圓形子震相當于一系列小震，在震源破裂過程中相繼被激發，最終釋放的能量在斷層面上不斷被疊加，達到模擬強震的目的。設圓形子震半徑為R、數目為N，則有：

(1)

式中，分形維數D=2，控制斷層面上圓形子震數量的分布及圓形子震的上升時間，P為比例常數：

(2)

式中，M0為地震矩，Δσ為應力降，Rmax為最大圓形子震半徑，Rmin為最小圓形子震半徑。對式(1)進行積分，可得半徑大于R且小于Rmax圓形子震的分布數量N(R)：

(3)

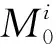
(4)

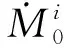
(5)

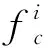
(6)

式中，β為剪切波的速度。斷層面上滑動位移量的空間分布由圓形子震滑動位移量疊加得到，第i個圓形子震的滑動位移量ΔUi為[1]：

(7)

式中，C為依賴斷層類型的常數，μ為介質剪切模量。

2 地震數據與震源參數

本文研究區域(103°～105°E，31°～35°N)位于巴顏喀拉塊體，該塊體近年來地震頻發。九寨溝地震后，中國地震臺網中心等機構公布了其震源位置、地震矩、震源深度、斷層節面的走向、傾角和滑動角等震源參數(表1)，其中，根據美國地質調查局的研究，斷層節面Ⅱ為實際斷層面[1]，因此本文取節面Ⅱ進行研究。

表1 九寨溝地震震源參數

基于孟令媛等[9]對余震分布情況及斷層面上滑動位移的反演結果，建立長30 km、寬20 km的斷層模型，并將其劃分為150個2 km×2 km的正方形子斷層。斷層面上圓形子震的分布如圖1所示，其中圓形子震地震矩的總和等于總地震矩。通過式(7)計算得到斷層面上滑動位移量的不均勻分布，如圖2所示。九寨溝地震震中距150 km區域范圍內臺站信息如表2所示，九寨溝地區介質速度信息(圖3)來自全球地殼模型Crust1.0(https:∥igppweb.ucsd.edu/～gabi/crust1.html)，臺站位置分布如圖4所示。對所有臺站觀測數據進行基線校準和濾波處理，帶通濾波范圍為0.1～20 Hz。

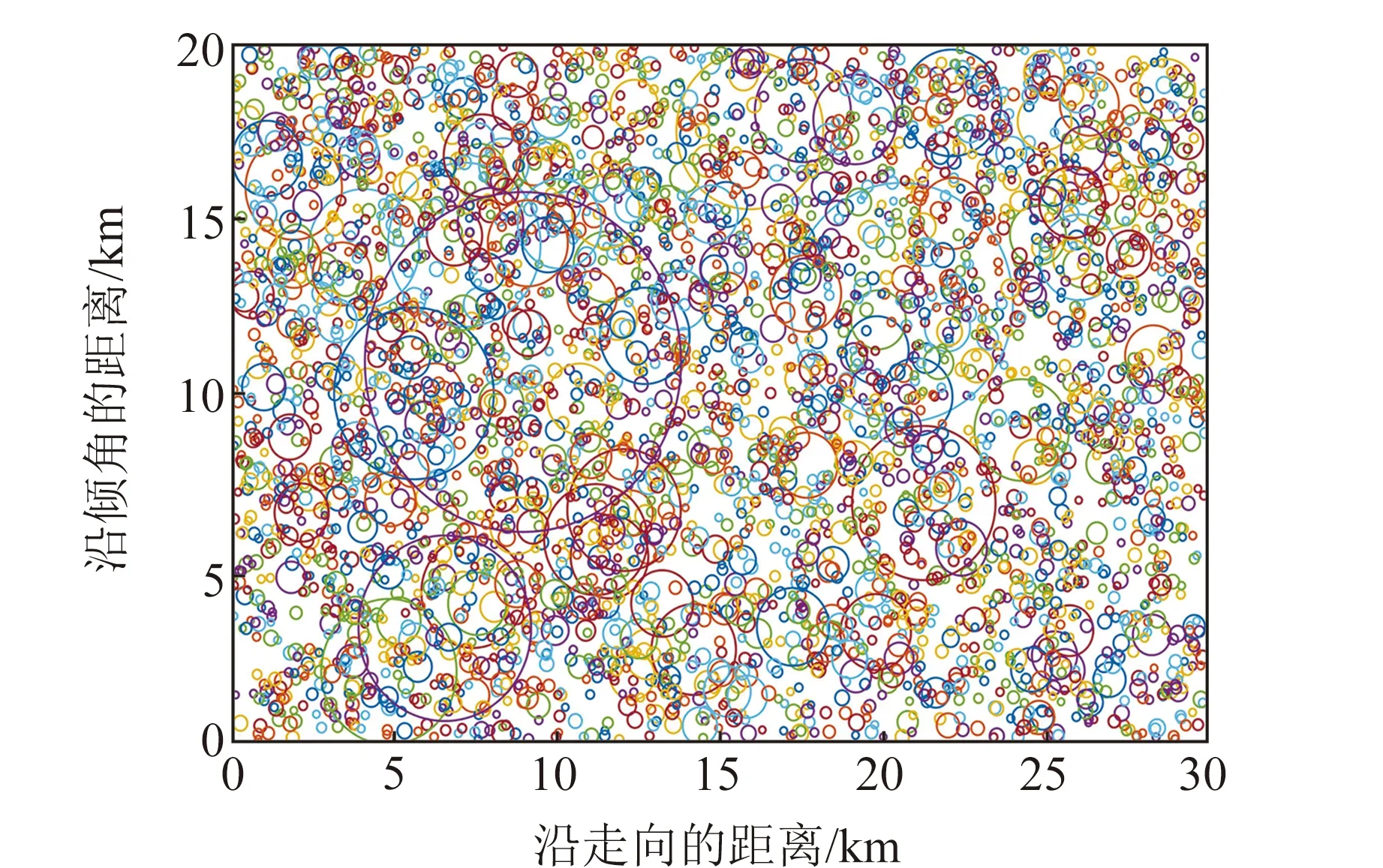
圖1 斷層面上圓形子震分布Fig.1 Distribution of circular subevents on the fault plane

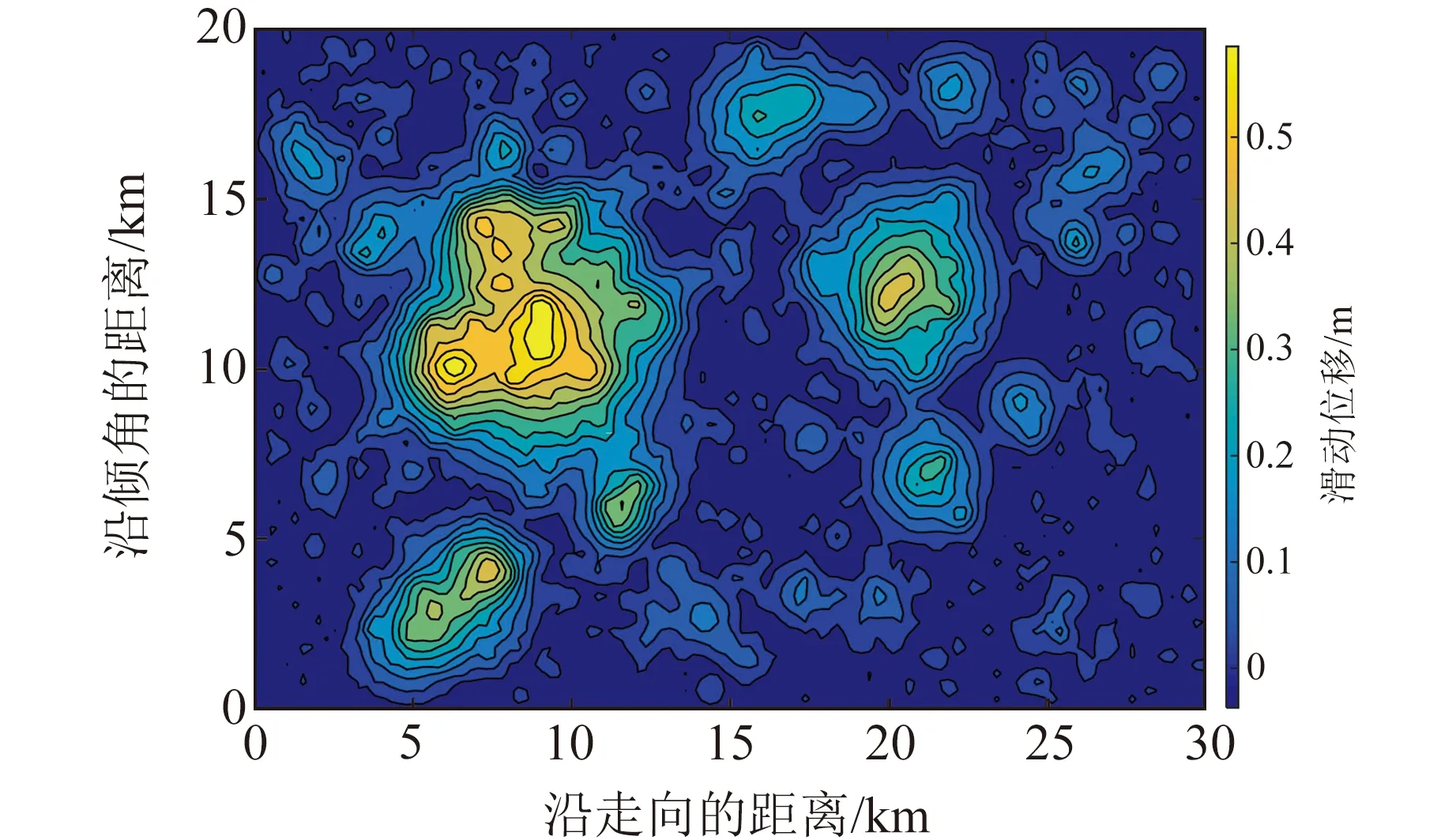
圖2 斷層面上滑移量的不均勻分布Fig.2 Non-uniform distribution of slip on the fault plane

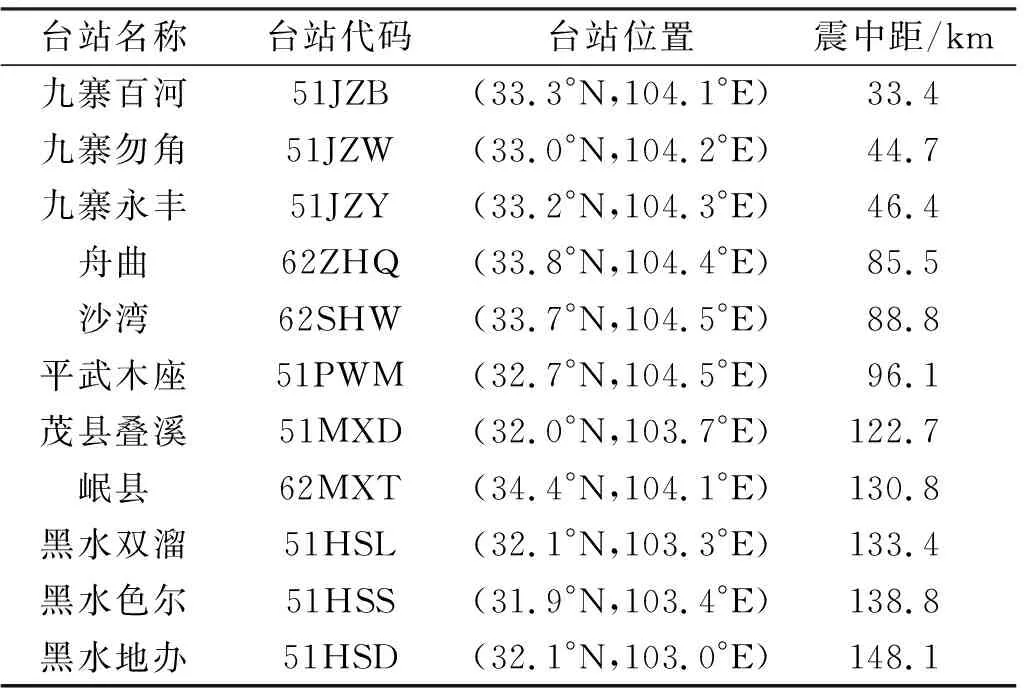
表2 臺站信息

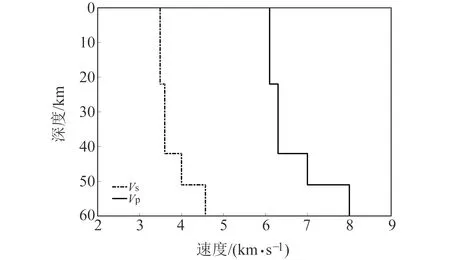
圖3 九寨溝地區速度模型Fig.3 Velocity model of the Jiuzhaigou region

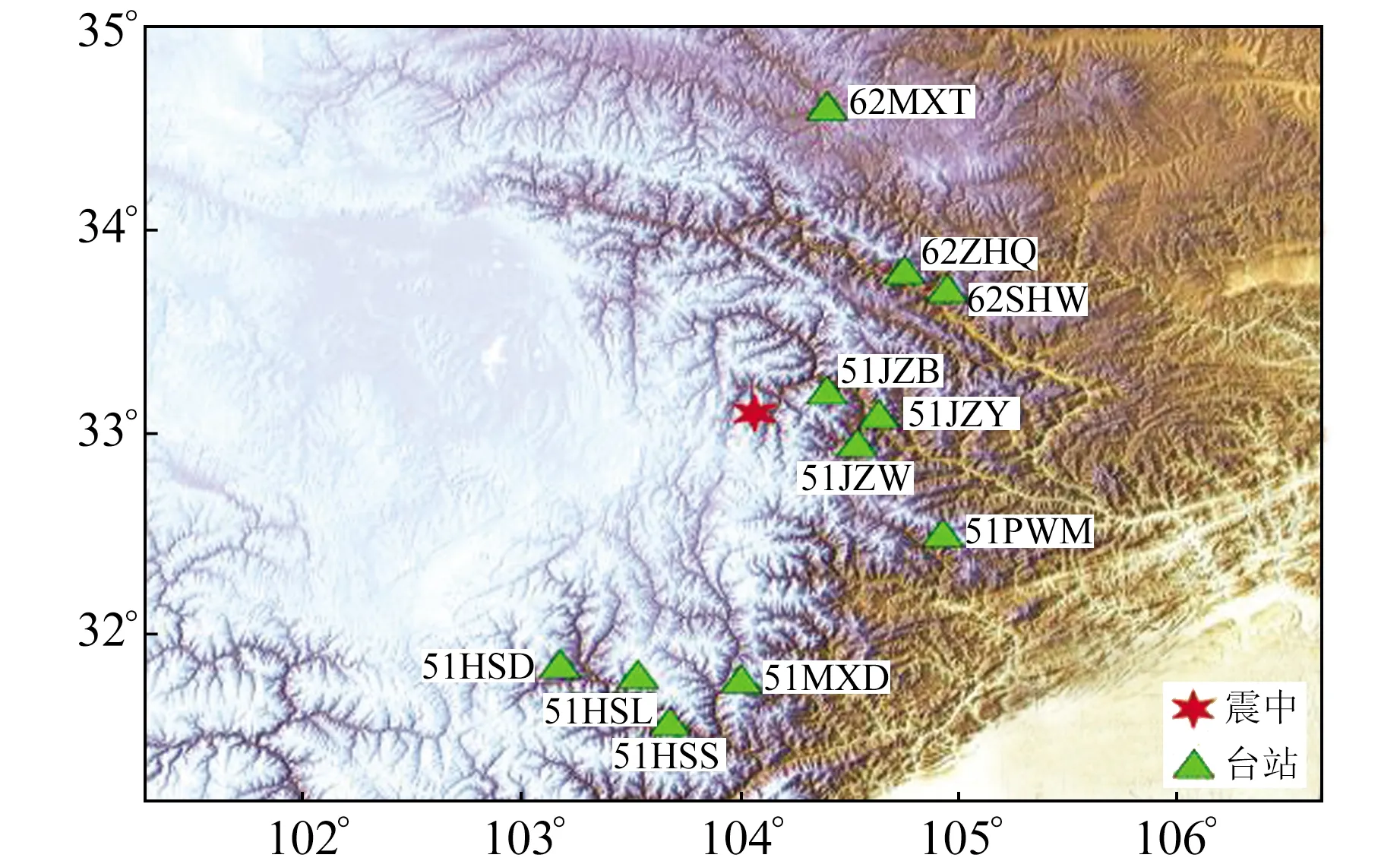
圖4 臺站分布Fig.4 Distribution of the stations

3 參數敏感性分析

在運動學震源模型中，斷層的破裂面積、長度、寬度、埋置深度、走向、傾角和滑移角等是描述斷層特征的參數；地震矩、應力降、平均滑動時間、平均破裂速度、破裂方式和初始破裂點位置等是描述平均破裂過程的參數。這些震源參數控制著地震動強度和分布[10]，分析這些參數的影響規律可為地震動合成精度提供保證。本文首先以無強震觀測記錄為前提，研究地震矩、應力降、破裂速度、子斷層尺寸、震源深度、斷層走向、傾角和滑移角等8個震源參數在所有合理取值范圍內對復合震源模型計算結果的影響程度；然后根據九寨溝地震觀測數據確定適合的震源參數研究范圍，并進行敏感性規律分析，在其他參數保持不變的條件下，僅改變單個參數變量，利用評價指標比較分析計算結果，總結震源參數對地震動計算的影響規律。

3.1 評價參數和評價指標

為表征震源參數對臺站NS和EW向峰值加速度(peak ground acceleration，PGA)的影響，用誤差值E表示計算的PGA相對于觀測的PGA的變化：

E=|AOBS-ASYN|/AOBS×100%

(8)

式中，AOBS為觀測的PGA，ASYN為計算的PGA。

地震動強度主要用PGA、峰值速度或譜加速度等地震動參數表達。本文以PGA為例，根據王德才等[11]的參數敏感性分析模型，通過計算模型偏差和模型標準差討論不同震源參數對PGA的影響。

用模型偏差B表征計算值和觀測值之間的差異，偏差越大，計算值越偏離觀測數據：

(9)

式中，M為總臺站數。

用模型標準差S描述數據離散程度，標準差越大，數據波動性越強：

(10)

3.2 參數敏感性分析結果

首先選取地震矩、應力降、破裂速度、子斷層尺寸、震源深度、斷層走向、傾角和滑移角等8個震源參數的最大合理取值范圍，計算得到不同震源參數數值下臺站NS和EW向的PGA，然后以模型偏差B和標準差S為衡量標準，分析8個震源參數對復合震源模型計算結果的影響程度。

地震矩根據Hanks等[12]提出的地震矩與矩震級的關系，在強震6～8級范圍內取值計算，間隔為1×1018Nm；應力降參考王振宇等[13]的取值范圍10～200 bar，間隔為5 bar；斷層的平均破裂速度約為剪切波速的0.6～0.9倍[14]，本文選取此區間，并設定區間間隔為0.05；子斷層尺寸取值分別為1 km×1 km、2 km×2 km、6 km×6 km、8 km×8 km和10 km×10 km；震源深度范圍選定為0～30 km，取值間隔為1 km；斷層走向、傾角和滑移角依據理論范圍分別取0°～360°、0°～90°和-180°～180°，取值間隔分別為10°、5°和10°。

8個震源參數取值范圍和梯度各不相同，本文通過式(9)和式(10)計算出相應PGA的偏差和標準差，然后將每個震源參數下PGA偏差、標準差的最大值及最小值作差，消除AOBS實測數據的影響，得到每個震源參數下PGA偏差和標準差的變化幅度，結果如圖5所示。由圖5可知，地震矩、應力降、破裂速度、子斷層尺寸和震源深度對PGA偏差和標準差的影響明顯，其中地震矩和應力降影響更突出；斷層走向、傾角和滑移角對PGA偏差和標準差的影響極不明顯。根據地震學理論，地震矩直接決定地震釋放的能量大小，地震矩越大，地震波攜帶的能量越多，使得整體加速度計算值增加；應力降表示斷層上某點破裂前后的應力強度變化，應力降越大，斷層上釋放的應力越多；破裂速度決定斷層面圓形子震的發震時間，間接影響整個斷層面的破裂過程；子斷層尺寸的劃分會對斷層面上滑移量分布產生很大的影響；震級相同的地震，震源越淺，造成的破壞越嚴重。

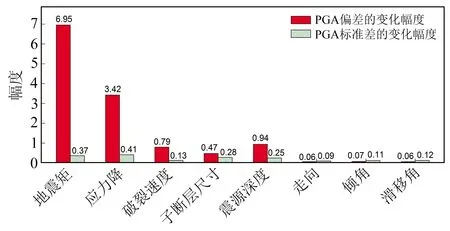
圖5 不同震源參數對PGA偏差和標準差的影響幅度Fig.5 The influence amplitude of different sourceparameters on PGA deviation and standard deviation

基于8個震源參數的影響規律，結合表1不同研究機構和眾多學者[2-4,8]提供的震源參數，確定九寨溝地震震源參數研究范圍，進一步研究8個震源參數對九寨溝11個臺站NS和EW向PGA的影響大小和規律，取值間隔如圖6所示。

從圖6看出，地震矩、應力降、破裂速度、子斷層尺寸和震源深度對臺站PGA的影響大；斷層走向、傾角和滑移角對臺站PGA的影響小。說明在應用復合震源模型計算九寨溝地震時，即使8個震源參數取值范圍有所限制，沒有取到理論范圍內的所有值，但其對計算結果的影響規律基本與圖5一致。

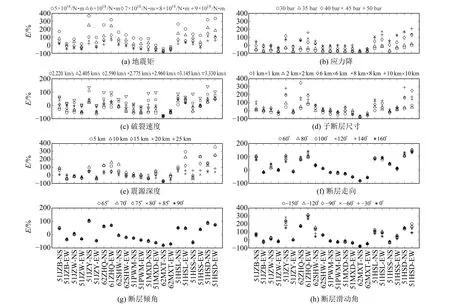
圖6 不同震源參數對臺站PGA的影響Fig.6 Influence of different source parameters on station PGA

圖7為地震矩、應力降、破裂速度、子斷層尺寸和震源深度等5個震源參數對九寨溝地震地震動模擬的影響規律，其中實心點表示本文取值。由表3和圖7可知，受地震矩影響，PGA的偏差變化范圍超過1，PGA的偏差和標準差隨地震矩的增加而減小，其中PGA的偏差下降趨勢近似為線性變化，地震矩為7×1018Nm時，PGA的偏差基本為0，同時PGA的標準差也較小。應力降越大，臺站整體PGA越大，PGA的偏差越小，應力降為40 bar時，PGA的偏差接近于0，這與俞瑞芳等[15]應用隨機有限斷層法得到PGA隨著應力降增大而逐漸增加的結論類似。破裂速度越大，PGA的偏差越小，當破裂速度等于剪切速度0.8倍(2.96 km/s)時，偏差接近于0，此時標準差也最小，與傅磊等[16]應用隨機有限斷層法和李宗超等[4]應用經驗格林函數法在地震模擬過程中選取的破裂速度與剪切速度的比例關系一致，PGA的偏差變化范圍為0.9。子斷層尺寸越小，PGA的偏差越小，最佳尺寸為2 km×2 km，此時標準差也為最小值，與Dang等[1]利用隨機有限斷層法的研究結論相同。震源深度在20 km處PGA的偏差幾乎為0，同時標準差最小，隨著震源深度的增加，PGA的偏差增長趨勢變緩；而且如圖6所示，震源深度為25 km時，大部分臺站的峰值加速度很小，與劉啟方等[10]運用震源位錯模型得到的研究結果相似。

表3 不同震源參數PGA偏差和標準差統計結果

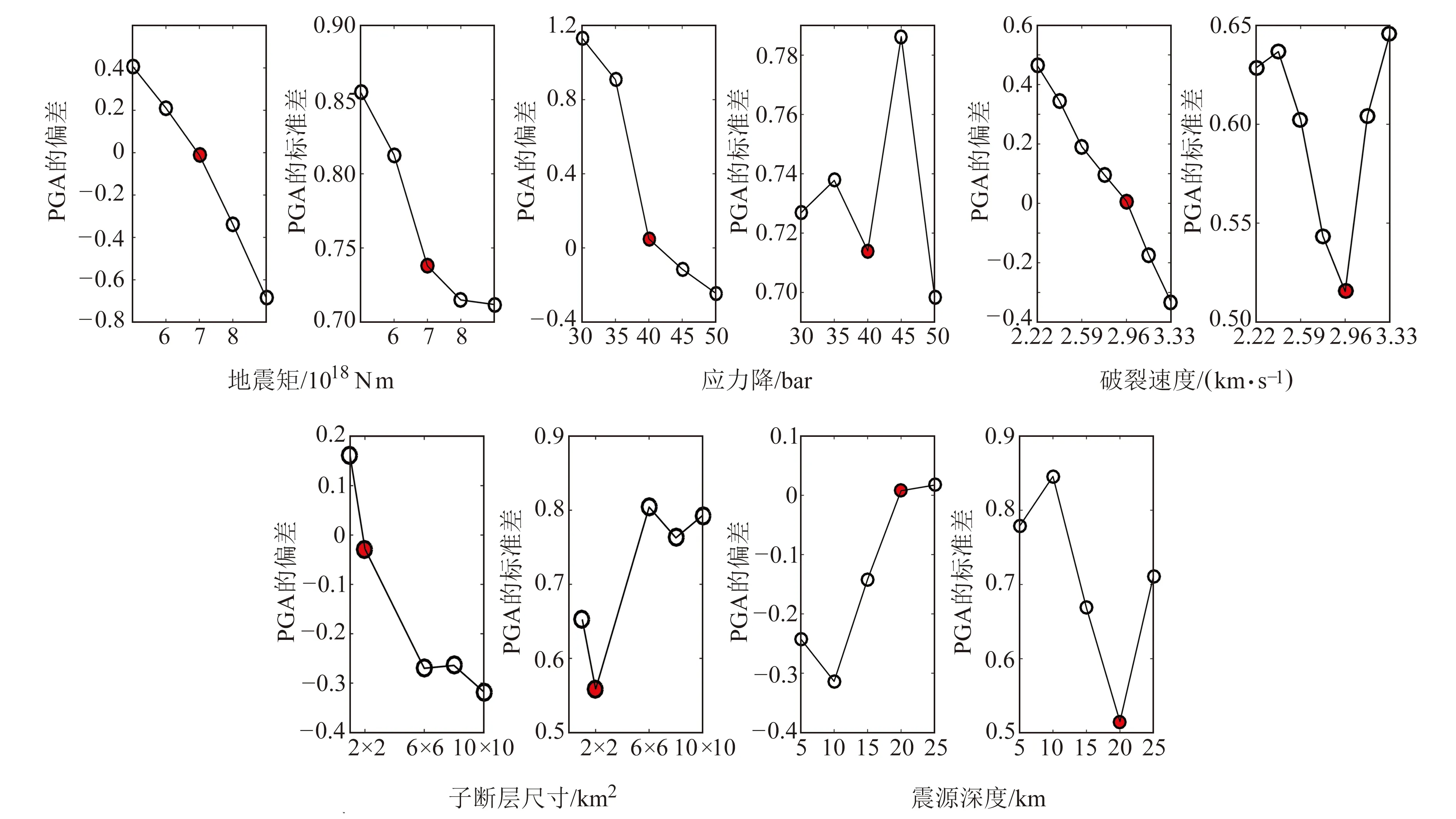
圖7 不同震源參數對PGA偏差和標準差的影響Fig.7 Influence of different source parameters on PGA deviation and standard deviation

斷層走向、傾角和滑移角中，PGA的偏差最大變化幅度為0.08，標準差最大變化幅度僅為0.1，對計算結果影響不明顯，與王德才等[11]采用混合方法[17]和隨機方法[18]研究的結果一致。

3.3 地震輸入參數組合

由上文分析結果可知，震源參數整體對PGA偏差影響幅度大，對標準差影響幅度相對較小，因此以PGA的偏差為主要衡量標準，標準差為次要標準，得到一組與觀測記錄擬合效果較好的震源參數。從表1各機構提供的數據中選取地震矩、破裂速度、子斷層尺寸、震源深度、斷層走向、傾角和滑移角；應力降參考Sun等[3]的結果，品質因子Q(f)和高頻衰減kappa值參考孟令媛等[9]的結果，具體數值如表4所示。

表4 九寨溝地震復合震源模型輸入的震源物理參數

4 地震動模擬結果分析

根據式(8)計算11個臺站NS和EW向PGA的相對誤差，并分別與Dang等[1]和李宗超等[4]的計算結果進行對比(圖8)。可以看出，11個臺站NS和EW向PGA相對誤差均小于50%。62SHW站NS和EW向PGA相對誤差最小，均小于3%；51HSL站NS向、51HSD站NS和EW向PGA誤差較大，且計算值均大于觀測值，主要原因可能是臺站震中距較大，導致傳播過程中散射的復雜性增加，同時，臺站局部山體地形引起的場地效應也會增加計算誤差。11個臺站NS和EW向PGA相對誤差均在20%以內，說明所有臺站PGA與實際數據相比誤差小。與Dang等[1]和李宗超等[4]的計算結果相比，除李宗超等[4]51JZY站EW向、62ZHQ站NS向和62MXT站NS向外，本文各臺站PGA相對誤差均較優。為方便直觀地進行地震動持時和波形對比，所有時程均截取45 s時間窗(圖9)，臺站加速度記錄數據中最小PGA為2.75 cm/s2，為避免地震動持時出現零持時這種不合理狀態，選取Bolt持時的閾值為0.5倍的PGA 作為計算相對Bolt持時的閾值[19]。從圖9看出，個別臺站誤差較大，但大多數臺站地震動持時基本保持一致。如圖10所示，合成反應譜整體變化趨勢與觀測反應譜一致，說明11個臺站的峰值加速度、地震動持時和反應譜整體擬合效果較好，與觀測數據較為符合。

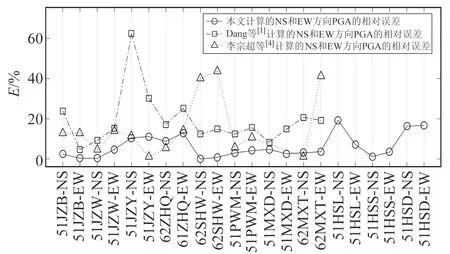
圖8 不同臺站NS和EW向PGA的相對誤差對比Fig.8 Comparison of relative errors of PGA in NS and EW directions at different stations

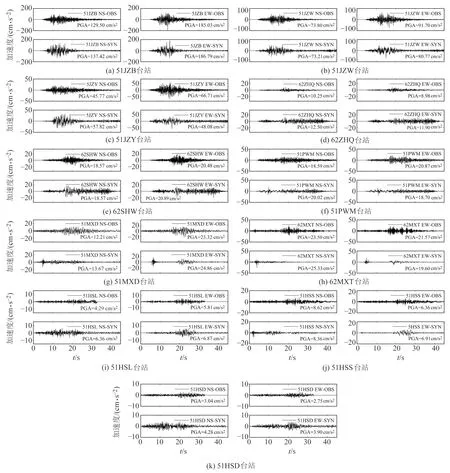
圖9 不同臺站NS和EW向加速度時程Fig.9 Time history of acceleration in NS and EW directions at different stations

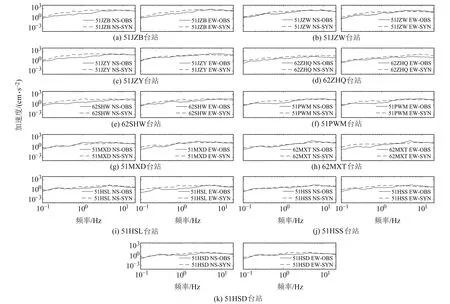
圖10 不同臺站合成和觀測加速度反應譜Fig.10 Synthetic and observed acceleration response spectra at different stations

部分臺站地震動三要素計算結果精度偏低的可能原因是：1)沒有充分考慮地形因素對地震動的影響，部分臺站如51HSL、51HSS和51HSD等位于山體上，山體地形的高度及底部延展距離對斷層動力學破裂過程影響較大，進而影響到相應的地面地震動分布[20]，山體的坡角、地震動入射角度會對山體地震動產生抑制作用，導致臺站PGA變小[21]；2)本文在計算地震動時采用各向同性散射模型，但實際地震波在地殼介質中的傳播是各向異性的，而且隨著傳播路徑的增加，散射的影響也會逐漸加強；3)有些震源參數的選取進行了簡化，在地震動模擬過程中假定某些參數(如應力降和破裂速度)為常數，忽略了參數與時間和空間的相關性；4)多數臺站低頻段反應譜模擬結果高于觀測值，可能是由于本文模型在破裂過程中沒有考慮到圓形子震傾角的可變性，或是在合成格林函數中未納入小尺度地殼非均勻性的散射效應[22]。

PGA是表征地震能量的重要指標之一，能夠為建筑物抗震設防提供合理的參考依據。綜合現有11個臺站PGA的觀測值和計算值可以得到九寨溝地震PGA 空間分布特征，如圖11所示。由圖11可知，隨著震中距增大，NS和EW向PGA從震源中心呈橢圓形向四周衰減擴散，長軸方向大致呈SW走向，這可能與斷層破裂的方向性有關，且2個方向PGA最大值均出現在51JZB站；在51MXD和51PWM站之間有一個PGA值未連通的區域，可能是由于該區域缺少合適的臺站記錄所致。總體而言，PGA計算值和觀測值的空間分布特征較為一致。

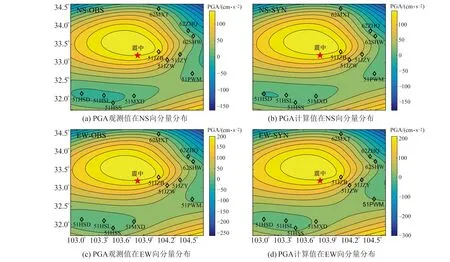
圖11 九寨溝地震PGA空間分布特征Fig.11 PGA spatial distribution characteristics of Jiuzhaigou earthquake

5 結 語

1)在最大合理變化范圍內，相對于斷層走向、傾角和滑移角，地震矩、應力降、破裂速度、子斷層尺寸和震源深度對地震動計算結果影響較大。

2)震源參數敏感性分析規律為九寨溝地震地震動模擬的參數選取提供了依據，進而得到一組合理的震源參數組合，同時能夠獲得九寨溝地區內任意一點PGA的變化區間。這一結論可以進一步推廣到其他缺乏強震觀測記錄的場地，計算出該區域強度特征的上限值，為建筑物抗震設防提供依據。

3)復合震源模型強地震動模擬了特定圓形子震在斷層上的破裂過程、斷層面上滑動位移的不均勻空間分布以及震源時間函數，計算結果可以再現九寨溝地震的地震動特征，模擬區域臺站的地震動PGA、地震動持時、反應譜和PGA分布特征與觀測值擬合較好，反應譜在高頻段擬合精度更高。