基于混合身份搜索黏菌優化的模糊C-均值聚類算法

賈鶴鳴，張棕淇，姜子超，馮榆淇

（1.三明學院 信息工程學院，福建 三明 365004; 2.東北林業大學 機電工程學院，黑龍江 哈爾濱 150040）

在計算科學中，機器學習是計算方法的重要研究領域。隨著人工智能技術的飛速發展，海量數據涌現于人類社會中，數據較易存儲，但數據處理的計算準確率與效率受數據維度與數目等原因的影響較大，而機器學習可以有效提升數據處理的效果[1-2]，但是要想通過機器學習獲得準確的模型，就需要大量具有標簽和規律特點的數據。這種需求正是數據預處理過程所能提供的。所以將優化技術用于數據預處理過程以獲得高質量數據，具有廣闊的應用場景及需求。如何進一步顯著提高數據預處理的性能已成為目前機器學習領域中的熱點內容。聚類分析因其獨特的優勢：能夠在無標簽、海量的數據中快速、準確挖掘數據自身的規律及特點，完成數據統計與分類任務，進而大幅度提升機器學習的準確性與效率[3]，成為數據預處理的重要技術之一。

作為聚類技術的其中一種方法，無監督機器學習聚類的實質是將物理或抽象對象的集合分成由類似的對象組成的多個類別的過程，這些由聚類所生成的簇是一組數據對象的集合，這些對象與同一個簇中的對象彼此相似，與其他簇中的對象相異，能夠揭示數據內部特有的信息價值[4]，完成數據分類任務。經過諸多學者深入研究，目前的主流聚類分析算法包含：基于密度的方法、基于網格的方法、基于層次的方法、基于模型的方法和基于劃分式方法等。其中，C-均值聚類[5]是一種廣泛應用于探索性數據分析、數據挖掘、機器學習、圖像檢索和數學編程中的聚類技術，但此方法計算和分類都局限于硬子空間集合，所以其存在時間復雜度高、對噪聲不敏感，處理數據維度較低等缺點與局限性。為改善其聚類效果，Dunn等[6]基于模糊數學的概念提出了模糊C-均值聚類(fuzzy C-mean, FCM)技術，使得分類問題不再局限于硬子空間集，每個樣本可同時隸屬于不同的類別，有效克服了C-均值聚類算法的缺點與局限，具有良好的聚類效果，但FCM依舊沒有解決經典聚類技術中所存在的初始化敏感、迭代的過程中易陷入局部最優、穩定性不足等問題。Kennedy等[7]通過模仿鳥群的覓食運動方式提出了一種粒子群優化(particle swarm optimization,PSO)算法，并將其應用于聚類問題中，效果良好；Niknam等[8]將蟻群優化和模擬退火相結合，提出了一種有效的混合進化算法，同樣應用于聚類問題，提高了數據分類的準確率；Ozturk等[9]利用改進后的二進制人工蜂群算法對聚類問題進行優化，顯著改善了數據處理的效率；蒙祖強等[10]提出一種混合蛙跳與陰影集優化的粗糙模糊聚類算法，效果顯著；張新明等[11]將灰狼優化(grey wolf optimizer, GWO)算法用于FCM的聚類問題，提升了實際聚類性能。以上所述研究表明，使用啟發式群智能優化算法對聚類分析問題進行優化可獲得良好的分類準確率與效率，因此本文基于以上研究的有效性以及模糊C均值自身不足引入新穎的啟發式群智能優化對FCM聚類技術加以改進研究。

啟發式群智能優化發展已近20余年，黏菌優化算法(slime mould algorithm, SMA)是Li等[12]最近基于黏菌覓食的策略提出的一種新穎、有效的優化算法，因其優化求解效果好，已有許多學者將其算法用于實際的工程優化問題中，如Zhou等[13]將SMA與WOA[14]算法相結合用于X射線圖像分割；Mostafa等[15]將SMA模型用于太陽能電池板最優模型參數提取；Mohamed Abdel-Basset等將SMA算法進行優化得到了一種高效的二進制黏菌算法[16]。Bogara等[17]基于青少年的成長軌跡進行建模分析，提出了一種青少年身份優化算法 (adolescent identity search algorithm, AISA)，其中特有的社會行為、榜樣機制與身份特征更新策略提高了群智能類算法的優化求解精度。近年來啟發式群智能優化算法多數應用于實際工程問題的參數優化，如賈鶴鳴等[1,3]利用此類算法同步優化支持向量機的參數選取與特征選擇，極大改善了數據分類的準確率，但此類算法難以改變自身的邏輯收斂效果，而聚類算法的核心是將一組數據集劃分成各個子集，兩者均為閉環迭代計算模式，因此本文將SMA優化作為一種聚類的迭代策略融入FCM算法中，對其進行計算優化。但SMA算法的收斂是以各黏菌領域作為主要搜索區域，若各粒子之間信息交流不夠緊密，容易導致收斂速率慢、求解精度低，搜索域重復等問題。因此本文通過融合AISA算法中的社會群體性迭代方式，提出了混合青少年搜索黏菌優化(adolescent identity search algorithm-slime mould algorithm, AISA-SMA)算法，以提高SMA算法尋優求解性能，減少算法的不穩定因素。在啟發式群智能優化FCM聚類中，利用AISA-SMA算法優秀的收斂效果，將其引入FCM聚類迭代過程中，提出新的融合聚類算法AISA-SMA-FCM來改善算法精度，以獲得更優秀的聚類效果。

本文首先將AISA算法與SMA算法進行混合改進研究，改善SMA算法的高維及混峰求解能力，并通過測試函數仿真實驗證明所提混合算法求解精度高，收斂能力強；隨后將本文混合AISASMA算法應用于FCM聚類技術當中，使得FCM算法每次迭代都具有開發和搜索兩種行為，并對經典UCI數據集進行聚類仿真測試，分析所得適應度值等指標，對比其他聚類方法證明AISA-SMA-FCM算法具有更優秀的聚類能力。

1 相關算法

1.1 模糊C-均值算法(FCM)

模糊C-均值聚類算法是用隸屬度來確定每個數據點屬于某個聚類程度的一種聚類算法，首先給出樣本觀測數據矩陣:

式中矩陣每行為一個樣本，每列為一個變量的n個觀測值，即式(1)是由n個樣本的p個觀測值構成的矩陣。

聚類目的是將這n個樣本劃分為c類（2＜c＜n），記V= （v1,v2,···,vc）為c個類的聚類中心，其中vi= （vi1,vi2,···,vip）（i=1,2,···,c）。 在 模 糊C均值聚類中，每個樣本是以一定的隸屬度劃分為某一類，其定義目標函數：

其中，U=(uik)c×n為 隸屬度矩陣，dik=||xk-vi||。J(U,V)表示各類中的樣本到該聚類中心的加權平方距離之和，權重是樣本xk屬于第i類隸屬度的m次方。模糊C均值聚類算法的聚類準則是求取U、V，使得J(U,V)取得最小值。模糊C均值聚類算法的具體步驟如下：

1）確定類的個數c，冪指數m(m＞1)和初始隸屬度矩陣U(0)=(u(ik0))，通常可以取[0,1]上均勻分布隨機數來確定隸屬度矩陣U(0)，令l= 1來表示第1步迭代(l迭代次數)。

2）計算第l步的聚類中心V(l)：

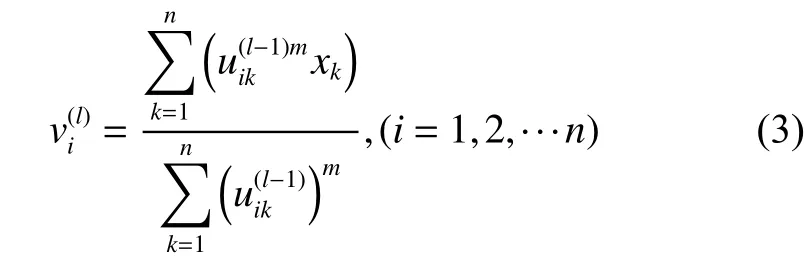
3）更新隸屬度矩陣U(l)：

4）計算目標函數J(l)，其中di(

kl)=||xk-v(il)||：

5）本文不設置停止精度，達到迭代上限，停止迭代，否則重復步驟2)。

6）經過不斷的迭代之后，可以求得最終的隸屬度矩陣U和聚類中心V，使得目標函數J(U,V)達到最小。根據最終的隸屬度矩陣的取值可以確定所有樣本的分類，當ujk=m1≤ai≤xc{uik}時，可以將xk歸為第k類，以完成分類過程。

1.2 黏菌算法(SMA)

黏菌算法是一種新穎的元啟發式群智能優化算法。該算法受啟發于黏菌擴散和覓食行為進而獲得連接食物的最佳路徑。其捕食過程主要分為兩個階段。

在黏菌覓食活動的第一階段，當黏菌搜索食物時，會根據空氣中的氣味來接近食物。在搜索第二階段中，黏菌開始包圍食物，模擬黏菌靜脈結構中的收縮模式，并根據食物質量調整位置。依據黏菌的搜索行為，可以利用式(6)來模擬其覓食行為

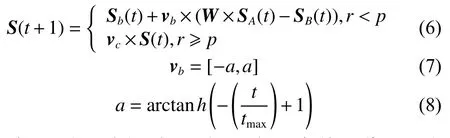
式中：vc從1線性減少到0；t表示當前迭代；tmax為最大迭代數；Xb為當前發現氣味濃度最高的位置；S(t)為當前黏菌的位置；S(t+1)為黏菌將要占據的下一個位置；SA、SB代表從黏菌群體中隨機選擇的兩個個體；r為0和1間隨機數；vb∈(-a,a)，W為權重：

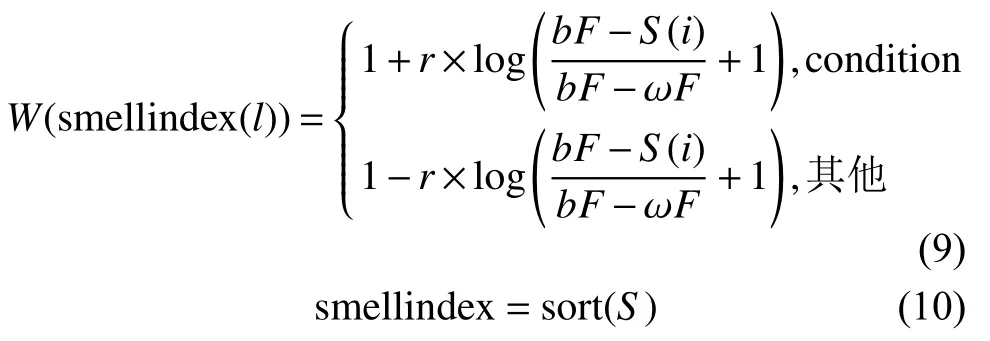
當食物濃度較高時，區域權重較大；反之權重轉移到其他區域。bF、 ωF分別為當前迭代中獲得的最佳、最差適應度值， c ondition 為S(i)在整個種群中排名靠前的半部分。參數p的表達式如下：

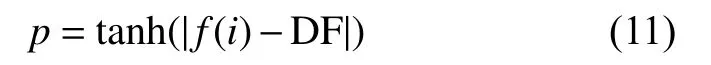
式中：i∈ 1,2,···,n，f(i)是當前的位置適應度，DF是所有迭代中獲得的最佳適應度值。

最后增補黏菌的全局搜索行為。此時對黏菌位置重新建模，得到完整的黏菌算法如下式所示。

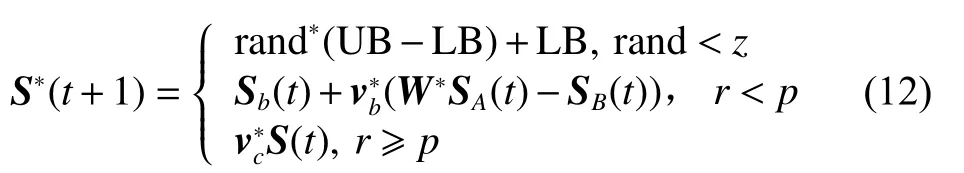
式中： r and 、r屬于[0,1]，UB和LB是搜索空間的上限和下限，z是黏菌將尋找其他食物來源或在當前最佳食物來源附近進行搜索的概率，W、vb、vc用于模擬黏菌靜脈寬度變化。

1.3 青少年身份搜索算法(AISA)

AISA算法通過身份特征(行為、喜好、思想、能力、信念等)來描述青少年的身份，本算法中青少年通過推理觀察社會行為、榜樣機制和不良特征選擇這3種策略來形成自己的身份。

1）推理觀察社會行為：青少年可以通過觀察并推理同伴群體的行為，來形成自己的身份。假定青少年可以通過識別組中的最佳特征并模仿他們，其中青少年的最佳身份為局部最佳適應度。通過Chebyshev函數連接功能網絡，并通過最小二乘法估計實現局部優化，所涉及切比雪夫多項式{Tk(x)}k-0,1,2,···遞歸方 程如下：

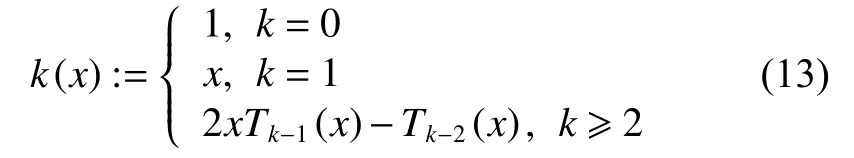
其中k是Chebyshev多項式系數。歸一化后的初始種群矩陣定義為，算法每個輸入元素定義如式(14)：

本文采用wj∈R1×k為權重輸入，通過式(16)獲得局部適應度值，?為次回歸向量，如式(15)中矩陣所示。

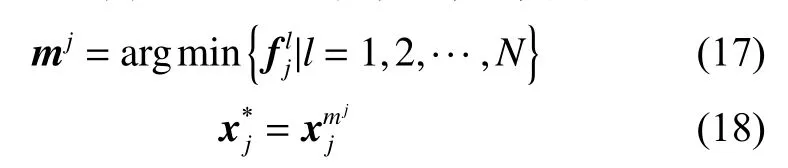
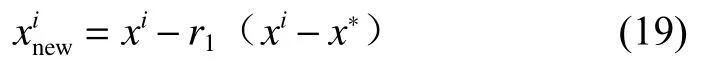
2）榜樣機制：青少年通過模仿具有較高地位、權力和威望的榜樣來形成自己身份，榜樣為具有最佳適應度值的個體。

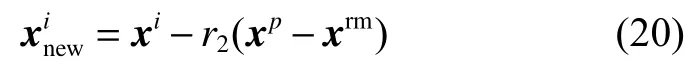
式中：r2是[0,1]中的隨機數；xrm表示榜樣（最佳個人）。p≠rm，xp表示p個青少年。

3）不良特征選擇：青少年可能會具有吸煙、吸毒和霸凌等不良特征，假定不良特征xu是從總體矩陣中隨機選擇的元素，青春期身份可以通過式(21)表示：

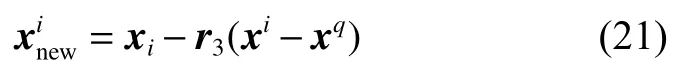
式中：r3為[0,1]內均勻分布的1 ×n維數字行向量；xq表示如下所示的負同一性向量。

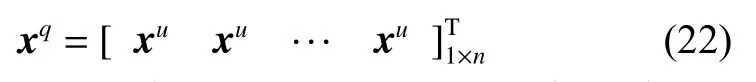
將3種結果組合，得到新的青少年身份身份，如式(23)所示，其中r4是[0,1]內的隨機數，用于3種不同策略的選擇。

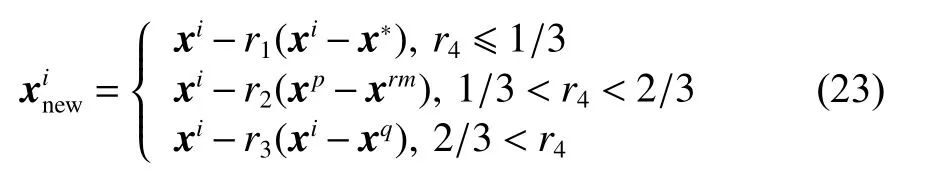
2 混合青少年搜索群體-黏菌算法

2.1 青少年-黏菌算法混合策略

黏菌算法是受到黏菌捕食中行為和形態的變化的啟發。在捕食的過程中，根據食物量的多少，黏菌的捕食行為將會產生正反饋和負反饋，從而在黏菌算法中總結出了3種捕食形態。對比于其他群智能類算法，如粒子群、灰狼、人工魚群或蝗蟲算法等依托于個體行為與群體行為相結合作為搜索方式的群智能優化算法，黏菌算法更類似于鯨魚算法、樽海鞘算法等在自身算法中憑借個體本身的多種探索、開發機制作為優化方式的算法。但這種以個體搜索作為優化策略核心的算法往往出現精度高的搜索特點，但是同時每個個體搜索機制中的廣域搜索和局部開發無法針對當前的迭代情況做到有效的平衡，個體與群體的聯系較弱，無法有效地學習其他個體的經驗，導致每次迭代效果較差，穩定性不足，針對混峰和多峰問題性能較弱等情況。因此本文將側重于將SMA算法與社會性質較強的AISA算法相結合，替換黏菌算法的部分搜索機制，使得SMA算法的每個個體具有社會屬性。從社會群體的角度調整探索與開發的比重，避免陷入局部最優，改善優化求解精度，增強穩定性。

在黏菌算法中，黏菌個體通過式(6)、(12)來進行迭代運算，其中式(12)是負責SMA算法的全局探索，黏菌個體概率z進行全局內的搜索。但SMA算法本身缺乏有效的探索機制，全局搜索是一種效率較低的搜索機制，單純的式(12)無法保證黏菌算法擁有足夠大搜索比重。所以本文將AISA算法中青少年不良特征選擇與SMA算法的全局域搜索相結合，拓展搜索范圍。更新后的公式為

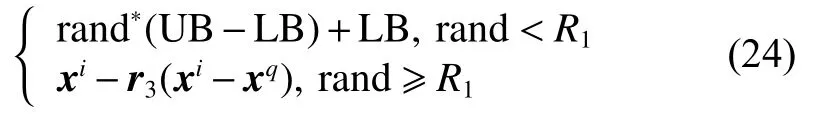
式中：xq為不良個體集合，xq表示負同一性向量，r3是一個1 ×n區間中均勻分布的數字行向量[0,1]。R1為社會選擇量，具體參數因數據而定，本文中為0.3。更新后的搜素公式將有較大的幾率根據目前黏菌群體的位置確定與開發區域相反的探索度較低區域，使得其他個體執行進行廣域搜索時可以提升搜索效率。

SMA算法中式(6)主要模仿了黏菌個體通過靜脈液寬進行包圍食物。在此過程中黏菌個體將通過向食物中心Sb(t)靠攏的方式進行包圍。但SA(t)-SB(t)使得黏菌個體在向最佳點靠攏時依舊具有局部探索的能力。這個策略本身十分優秀，但是在SMA-AISA算法的全局搜索部分已經加強了其搜索能力，則此部分算法中，將引入社會屬性，以獲得更為激進的開發策略以保證開發與搜索的平衡。將AISA算法中的青少年推理觀察社會行為與黏菌的食物包圍機制相結合，通過使用式(19)替換包圍機制中的食物最佳點Sb(t)，使得包圍機制可以向整個群體中局部最佳的位置進行包圍，提升探索效率。

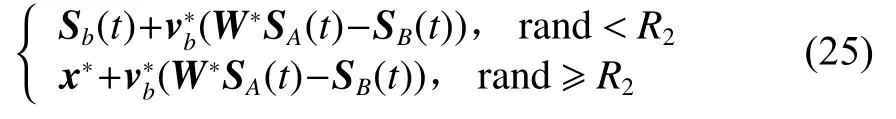
其中x*的計算式(19)與上文中AISA的青少年群體觀察機制相同，黏菌通過觀察群體行為，確定群體特征局部最優情況進行包圍。為防止過擬合的發生，設置R2為群體學習概率，群體學習概率決定策略烈度，具體參數因數據而定，本文設定為0.5。

SMA算法中式(6)主要模仿了黏菌個體對于食物的捕食機制，此公式是SMA算法主要的開發策略。但是在針對數據維度高且復雜的情況時，黏菌的開發能力不是十分理想。為了保證本文的收縮曲線能夠保持平滑和快速，將AISA算法中的榜樣學習機制作為增補機制，防止算法在前期過度收縮。具體計算公式如下：

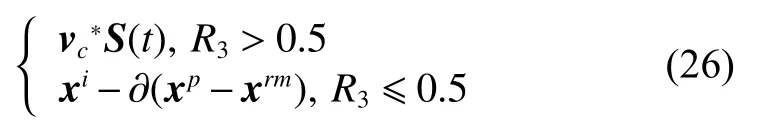
此更新公式中，?是青少年學習能力因子，公式為式(11)。學習因子保證了增補的公式(11)具有前期學習能力強，后期能力弱的特點，保證收斂速度。 ? (xp-xrm)調整收斂的步長，防止個體粒子在前期過度收斂陷入局部最佳，故設置R3為榜樣學習意愿，調整開發策略，具體參數因數據決定，本文設定為從1線性減少到0。綜合3種更新公式，得到新的啟發式混合群智能優化算法即青少年身份黏菌算法，實際運行過程如下所示。首先隨機初始化種群數值，產生隸屬度矩陣，確認參數，隨后將進入While循環，計算每個個體的適應度；并對個體進行操作，通過個體適應度計算其本身的黏菌權重如式(9)所示；隨后進入兩個判斷過程判斷幾率是否大于z；判斷隨機數是否大于R1，通過式(24)進行全球域搜索。最后若式(9)中幾率小于z；判斷隨機數是否大于R2，若大于則通過式(25)中第一策略對目前最優位置進行包圍和開發，反之則通過式(25)中第二策略通過青少年身份形成機制，優化收斂位置，進行包圍和開發。完成前兩個步驟后，個體通過式(26)進行捕食，通過劇烈收縮得到最佳適應值。完成循環，若迭代次數不滿足最大迭代次數。則跳轉回到While循環。

2.2 青少年-黏菌混合策略可行性分析

對AISA算法的搜索策略進行分析，可以發現其推理觀察社會行為機制如式(19)，是具有一定的創新性的。在本策略中通過Chebyshev函數連接功能網絡和最小二乘法估計實現局部優化。式(17)和式(18)使得算法可以根據當前群體適應度及特征，對最優點進行預估計，使得搜索個體在迭代的前期可以快速的向最優方向包圍和開發。這個策略相較于SMA算法所使用的策略，即利用目前個體最優解作為當前循環的收斂中心，在收斂速度方面具有很大優勢。所以本文在式(25)基礎上引入式(19)的局部預測機制，以改善其收斂速度較慢的弱點。

從SMA算法搜索策略進行分析，式(6)作為SMA算法核心公式，式(9)獨特的收縮包圍策略，使得SMA算法在局部的開發與探索通過權重的調整達到了很好的平衡，這使得該算法在處理數據結構相對簡單的局部尋優問題時有極其優異的性能。但也是因為這個機制，所以算法在迭代的過程中，局部的開發與探索占用了大量的計算資源，所以在面對數據結構復雜，維度較高的全局尋優問題時，無論精度還是收斂速度都顯示出了疲態。而AISA算法恰巧與其相反，得益于群體信息共享機制、相對高效的全局搜索機制，可使得AISA算法在面對數據結構復雜，維度較高的全局尋優問題時可以獲得良好的效果，這正是SMA算法所缺少的部分。所以本文在式(24)中引入了不良特征選擇策略，并且在式(26)中引入榜樣策略。這樣的改進目的是提升原算法的穩定性，及高緯度、復雜數據的處理能力。

3 AISA-SMA優化FCM聚類問題

FCM算法受模糊理論的影響，相較于C-均值(K-means)聚類為代表的硬子空間集聚類算法提供了更為靈活的聚類思路。但傳統的FCM算法在聚類的迭代時通常是一個中心連續移動的過程，這種聚類的方式無法兼顧全局的搜索，算法對初始化依賴程度較大并且容易陷入局部最佳；同時在高維度的聚類過程中，原算法通常無法有效地進行聚類分析。針對以上缺點，本文利用AISA-SMA算法精度高、收斂快和穩定性強的特點來優化原始FCM算法，通過調整迭代過程,即將AISA-SMA算法的搜索和開發特性引入FCM的每一次迭代過程，改善算法性能，這樣既引入了全新的搜索模式也保留模糊C均值算法的模糊數學思路。提出融合算法AISA-SMA-FCM，意在通過AISA-SMA算法較好的開發、探索能力和較強的收斂策略，提升FCM算法的單次循環聚類效果，以及盡量減少參數優化所增加的時間復雜度帶來的影響。使得原FCM算法聚類精度、穩定性及分類準確率得到提升。

3.1 混合AISA-SMA算法實現聚類功能

首先，AISA-SMA算法在初始化處理聚類問題時與其他聚類算法類似，首先在算法的初始階段讀入數據矩陣：

所得矩陣為N×a，其中N為數據特征數，a為數據總量。此時需要定義AISA-SMA算法迭代過程中的個體，賦予每個個體初值?。這一步與其他啟發式群智能優化算法中的初始化相同。

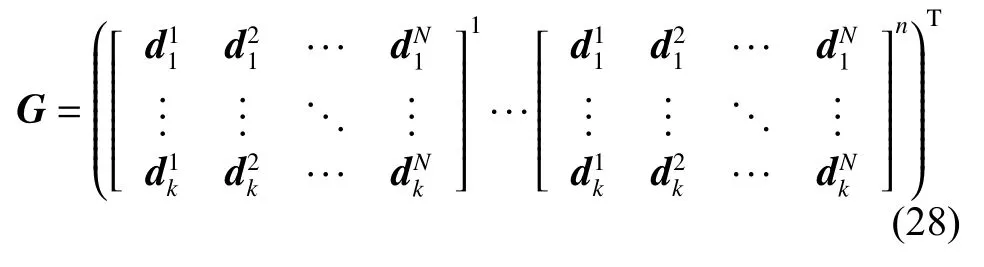
為一個N×K×n的矩陣，其中K為需要聚類的中心數，n為AISA-SMA算法中總共設定的個體數。每一個個體都為K個聚類中心，每個中心在初始化階段由式(29)隨機產生。

其次，所得到的初始化個體通過ASIA-SMA算法中數據更新式(24)～(26)迭代得到全新的聚類中心點位置，此過程可以視為N維空間中K×n個搜索粒子圍繞K個聚類中心進行的探索和開發。此時聚類中心點的適應度值應為K個聚類中心一組，由式(30)計算：

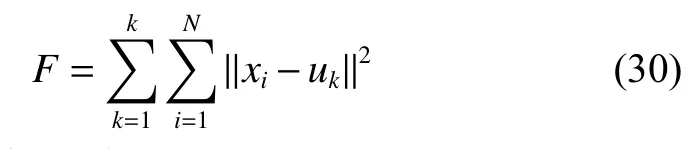
適應度越高則代表此時聚類結果的組內距最小，組間間距最大，即聚類結果的種群內部相似度更高，聚類效果越好。

具體AISA-SMA算法處理FCM聚類問題流程圖如圖1所示，其中AISA-SMA算法中的個體可以看做搜索粒子，通過式(24)～(26)對聚類中心的分布情況進行迭代優化，通過式(5)計算每個點的適應度值，找到適應度值最好的聚類中心分布，將聚類中心作為迭代結果輸出，完成數據分類任務。AISA-SMA算法具體的思路如下所示，首先讀取所聚類的數據，設置聚類數目，通過聚類數目，以聚類中心為個體進行AISA-SMA的初始化及參數設定。隨后通過式(30)計算每個個體的適應度。通過式(9)對每個個體計算權重，并判斷隨機數是否大于z，判斷是否進行全球化搜。最后通過R1，R2，R3決定式(24)～(26)的策略選擇。

圖1 啟發式智能優化用于FCM聚類Fig.1 Heuristic intelligent optimization for FCM clustering

3.2 混合AISA-SMA算法實現聚類功能

所提AISA-SMA-FCM聚類算法通過增補AISA-SMA聚類策略，替換部分FCM算法中隨機屬性高的策略。個體模仿AISA-SMA算法中的包圍捕食獵物的過程，探索開發聚類中心分布，對聚類中心的適應度進行迭代優化，具體實現過程如下：

算法初始階段，隨機生成隸屬度矩陣B，每個隸屬度矩陣應為a×K×n，隸屬的矩陣中，n為n個社會黏菌搜索粒子，每個搜索粒子所屬的隸屬度矩陣代表數據D中每個數據對于聚類中心的隸屬度。

4 仿真實驗與結果分析

為全面驗證改進算法的有效性，本節共設計兩部分對比實驗，一是選擇目前流行的啟發式智能優化算法進行標準測試函數實驗，測試算法理論尋優性能；二是利用經典UCI數據集測試對比其他算法用于聚類分析的優化效果。仿真實驗運行環境為Windows 7系統下使用MATLAB2016a，CPU：i5-6 500@3.3GHz，RAM：4GB。

4.1 標準測試函數尋優對比實驗

本節選擇 AISA-SMA、SMA[12]、AISA[17]、MRFO[18]、GWO[11]、PSO[19]算法在 15 個標準測試函數[3]上進行對比測試分析，其中測試集F1～F7為單峰函數，F8～F11為多峰函數，F12～F15為動態多峰函數。實驗測試評價基于運行10次搜索最優解的平均值。種群搜索個體設定為30，最大迭代次數為500，函數維度為30。

AISA-SMA與其他4種優化算法在15個標準測試函數的尋優實驗統計結果如表1所示。收斂曲線結果如圖2所示。

圖2 本文算法與其他算法適應度函數曲線Fig.2 The fitness function curves of the proposed and other algorithms

表1 AISA-SMA與其他優化的測試函數對比結果Table 1 Comparison results between AISA-SMA and other optimized test functions

數據表明，從均值上看，原SMA算法測試函數搜索最優解的表現良好，與本文算法具有一定的競爭力，但本文所提出的混合AISA-SMA在多數的單峰值與多峰值函數測試中可以搜尋到理論最優值，在動態多峰實驗中也基本可以搜尋到理論最佳值，性能相比SMA算法有了一定提升。AISA-SMA算法相比原AISA算法，在單峰的數據開發中具有很大優勢，在多峰和混峰問題中也良好地繼承了其良好的開發特性，很好地彌補了原SMA算法在面對復雜多峰問題開發能力不足的缺點。結合收斂曲線分析，結合后的AISA-SMA算法也繼承了AISA算法在前期激進的收斂策略，使得AISA-SMA算法收斂速度進一步提升，通過節約迭代次數的策略，相較于SMA算法提升計算效率。這進一步說明本文所提出的混合算法在空間搜索與計算求解中較其他算法具有明顯的優勢。

4.2 聚類分析對比實驗

為進一步驗證本文所提出混合優化用于FCM聚類，即AISA-SMA-FCM算法的有效性與優越性，選擇UCI數據庫[20]中的6個標準數據集進行聚類仿真實驗，具體數據集說明列于表2中。種群設置為50，最大迭代次數為200，運行環境與上節實驗相同。對比驗證的聚類方法采取SMA優化K-means算法與SMA優化FCM算法、FCM算法、以及MRFO優化FCM算法。實驗中每個算法獨立運行15次，統計計算適應度數據的平均值作為評價指標1，平均值越小表明算法聚類效果好，即聚類誤差值小；將15次最優平均適應度值的方差結果采取ANOVA箱型圖形式進行分析，作為評價指標2。每個圖中，箱圖的高度代表算法15次運算的數據分散程度，越短的箱圖表明10次結果越集中，同時也證明箱圖的噪聲越小，離群值較少，即算法穩定性越高；同時將適應度函數收斂曲線作為評價算法聚類效果的指標3，平滑、下降迅速，無較長延遲的曲線證明算法擁有更好的優化聚類性能；為了進一步體現算法的性能差異，將通過算法15次獨立運行的結果，進行非參數統計顯著性測試（Wilcoxon秩和檢驗），以及進行參數雙向方差分析的非參數模擬弗里德曼檢驗得出統計p值作為評價指標4。將算法15次獨立運行聚類結果的準確率，進行統計作為評價指標5。最后對比AISA-SMA-FCM及FCM算法過程散點圖對算法收斂速度進行評價為指標6，綜合指標1～6對算法進行綜合評價。

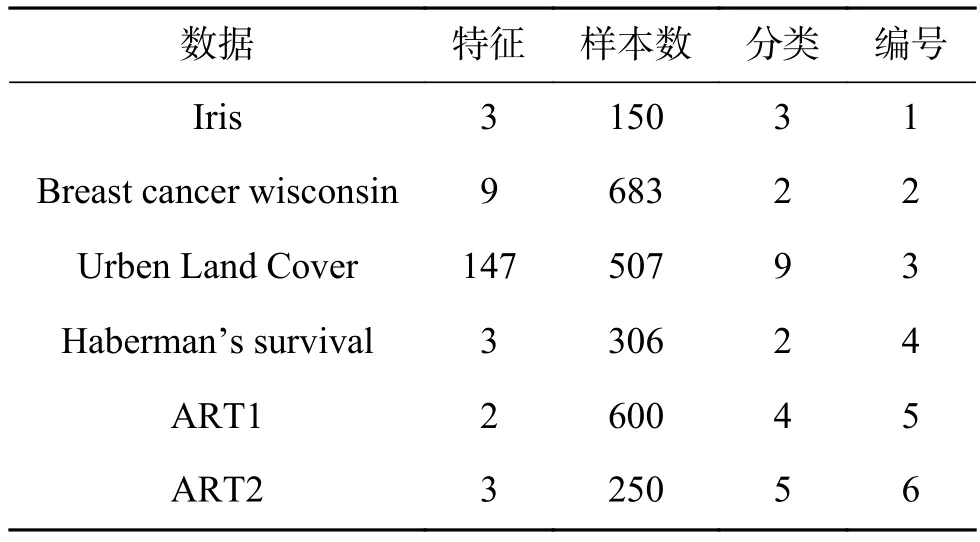
表2 UCI數據集的詳細信息Table 2 Details of UCI data sets

基于AISA-SMA-FCM算法與其他對比算法的聚類所得適應度值如表3所示。表中數據結果表明，AISA-SMA-FCM在平均適應度值中表現最優，相較于其他經典算法更為突出，得益于FCM算法主體思路的優勢與AISA-SMA算法優越性，表中用于優化FCM的算法都較優化K-means算法表現出更好的性能。因此，本文所提出的混合AISA-SMA算法更適合FCM聚類分析的優化處理。

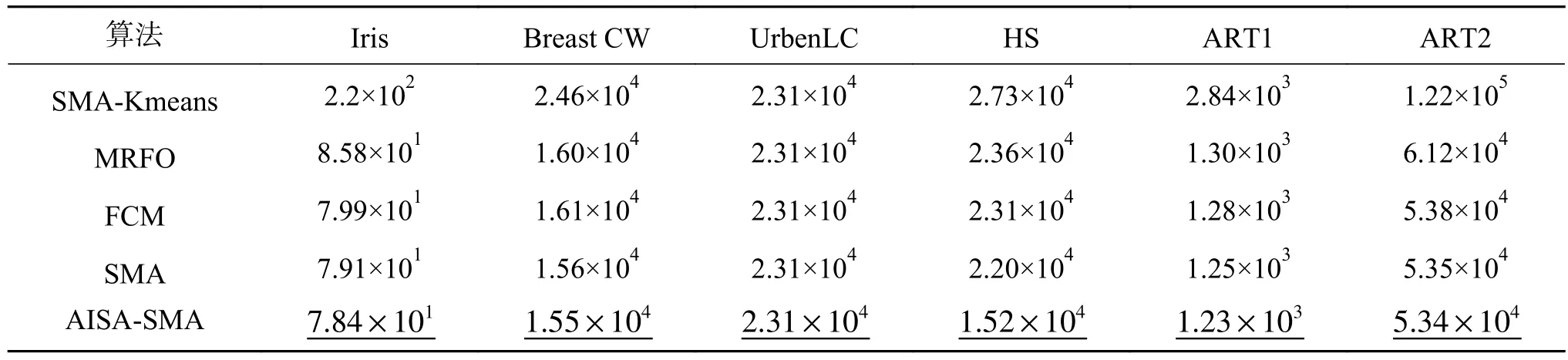
表3 AISA-SMA其他優化算法用于聚類的適應度值Table 3 The fitness value of AISA-SMA and other optimization algorithms for clustering

基于AISA-SMA-FCM算法與其他聚類方法的ANOVA箱型圖的測試對比結果如圖3所示。在6個數據集中，本文所提出的混合算法用于聚類時的計算穩定性最好，雖在Haberman’s Surival數據集中SMA的穩定性最佳，但其適應度值不如本文方法優秀，因此，綜合其他聚類來看，本文提出的方法用于FCM聚類分析問題時能夠獲得良好的聚類穩定性。

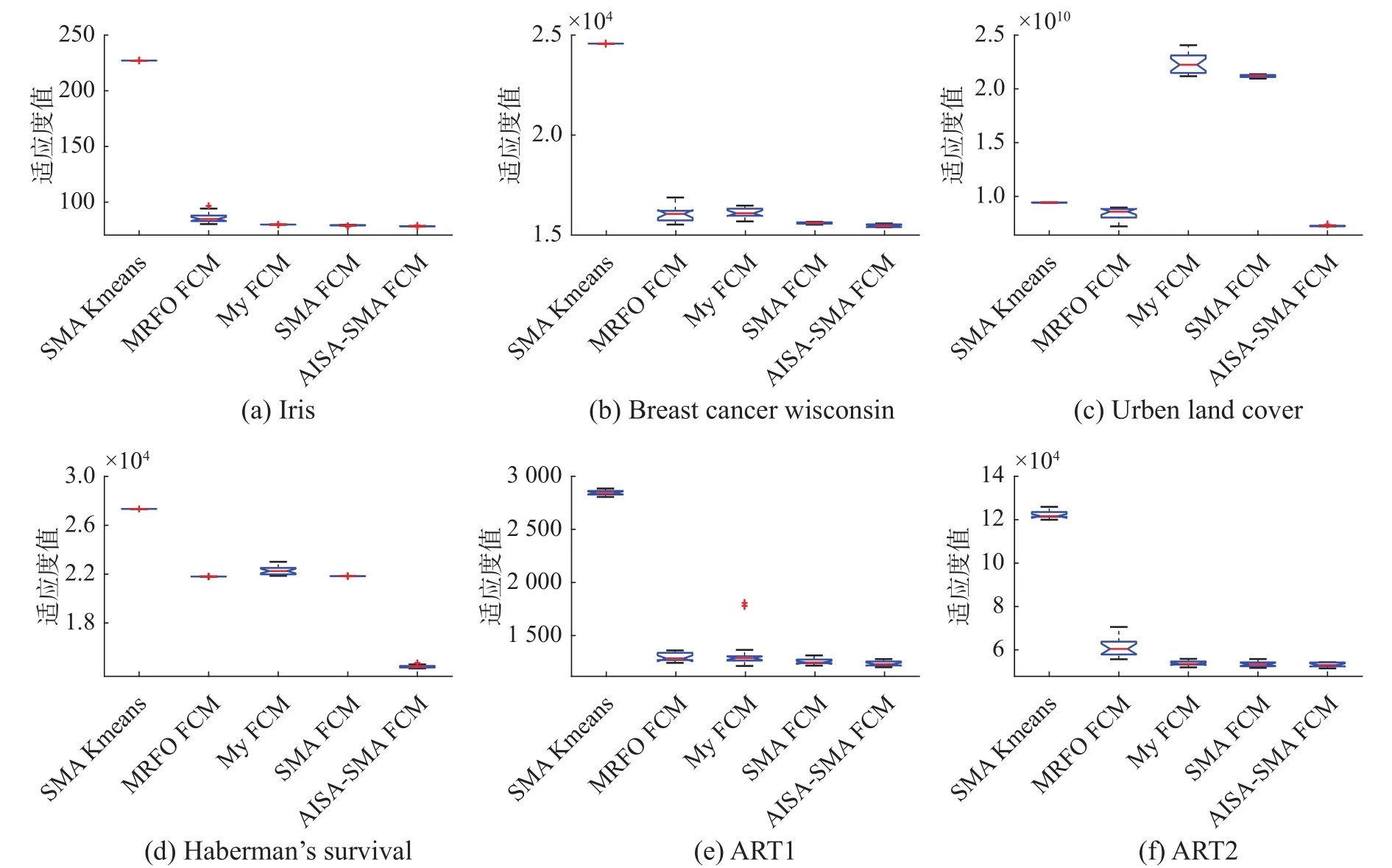
圖3 本文算法與其他算法適應度函數的ANOVA圖Fig.3 The ANOVA graphs of the fitness function of the proposed and other algorithms

基于AISA-SMA-FCM算法與其他聚類方法的適應度函數值收斂曲線如圖4所示。在數據集2與3中，本文所提算法收斂曲線效果最佳，用于解決FCM的聚類問題時能夠達到快速、準確收斂，同時搜尋到最佳的適應度值，數據集1與3中的結果表明，與經典的K-means聚類效果相比，FCM聚類技術更為優秀，本文算法用于FCM聚類優化效果顯著，FCM的搜索計算能力強。進一步驗證本文混合算法優化。

圖4 本文算法與其他算法適應度函數曲線Fig.4 The fitness function curves of the proposed and other algorithms

表4中給出了Wilcoxon秩和檢驗產生的p值，該值用于比較的兩個值為連續分布的樣本且具有相等的中間值。表中的本組實驗數據幾乎所有的值都低于0.05，因5%為顯著性水平值，零假設不成立，所以數據表明AISA-SMA-FCM算法在統計上是顯著的，實驗結果具有真實可信性。為進一步證明本文算法的優越性，驗證兩種算法的差異性，進行參數雙向方差分析的非參數模擬弗里德曼檢驗，所得結果如表5所示。AISA-SMA-FCM算法秩結果為1.9，表明其具有最良好的性能。綜上所述，實驗結果證明AISA-SMA算法在針對FCM聚類問題時，能夠提升FCM算法的性能，并且AISA-SMA-FCM算法相較于其他算法在聚類優化過程中效果顯著。

表4 本文算法與其他優化Wilcoxon檢驗p值Table 4 The Wilcoxon rank sum test p-value of the proposed and the other methods

表5 本文算法與其他優化的弗里德曼檢驗Table 5 The Friedman tests of the proposed and others

4.3 聚類結果對比實驗

4.3.1 聚類準確率對比試驗

本節將進一步對比AISA-SMA-FCM算法真實聚類效果。為了直觀對比5種算法的聚類效果，統計6個數據集的正確率，每個算法運行15次，取平均正確率，詳細結果如表6所示。由該表統計結果可以看出，在本文的6個數據集中，相較于其他算法，AISA-SMA算法分類準確率較高。AISA-SMA算法對于UrbenLC、ART1、ART2數據集，相較于基礎FCM及SMA算法提升明顯。但對于聚類中心數較高的情況例如UrbenLC，本算法依舊無法進行有效的分類，同時對于聚類趨勢不明顯的數據集如HS，本文算法也無法做到有效分類。綜上所述，AISA-SMA針對多中心、混雜數據集，依然還具有一定的提升空間。

表6 本文算法與其他算法的平均準確率Table 6 Average correct rate of the proposed and others %

4.3.2 聚類進程對比試驗

本節將對聚類過程進行探討，選擇Iris、HS、ART1、ART2 4個數據集，統計FCM及AISA-SMA算法在5次及20次迭代時的聚類效果，具體結果如圖5所示。從圖中ART1、ART2及HS數據集可知，在5次迭代時AISA-SMA算法已經具有基本分類模型，相較于FCM收斂較快；分析Iris數據集可知，兩聚類算法在20次時都已經收斂，但分類效果AISA-SMA算法明顯優于FCM算法，聚類群落清晰。因此通過測試結果可知，AISA-SMA算法相較于FCM算法具有響應速度快，分類效果好的優點，在相同的迭代次數下，聚類群體形態明顯好于原生FCM算法，其中的ART2及Iris數據集效果更為突出。綜上所述，AISA-SMA算法在聚類準確度、收斂速度及穩定性方面具有一定提升，效果較好。

圖5 本文算法與其他算法的聚類過程Fig.5 The Clustering process of the proposed and others

5 結論

本文提出了一種混合SMA與AISA算法來優化模糊C-均值的聚類方法，算法首先將SMA與AISA進行混合優化，利用AISA算法中的青少年社會機制，改善SMA算法中的全局搜索和局部開發性能，測試函數實驗表明混合算法計算求解性能優越；對于原FCM算法采取AISA-SMA算法對其迭代優化，提出AISA-SMA-FCM聚類算法以改善原聚類方法的聚類效率及精度，仿真結果證明AISA-SMA-FCM聚類算法在計算穩定性和收斂精度方面均具有較大的提升。如何提升算法在更高維度數據聚類分析中仍具有穩定、準確的效果是未來的研究方向，同時可探索將混合算法AISA-SMA運用到更多工程優化計算中。