擬合函數(shù)—神經(jīng)網(wǎng)絡協(xié)同的頁巖氣井產(chǎn)能預測模型

胡曉東，涂志勇，羅英浩，周福建，李宇嬌，劉健，易普康

中國石油大學(北京)人工智能學院，北京 102249

0 前言

頁巖氣壓裂后產(chǎn)能預測對于水平井壓裂效果評價和生產(chǎn)參數(shù)優(yōu)化具有重要意義。傳統(tǒng)的壓后產(chǎn)能預測方法包含解析法[1-3]、半解析法[4-6]、數(shù)值模擬法[7-8]和遞減曲線擬合法[9-10]等。傳統(tǒng)解析和數(shù)值模擬方法存在計算復雜、多物理場耦合困難等問題。而基于遞減曲線等傳統(tǒng)經(jīng)驗模型只能粗略描述地遞減特征，難以準確而全面地表征復雜條件下的生產(chǎn)動態(tài)。

20世紀以來，許多學者嘗試將基于數(shù)據(jù)驅(qū)動的機器學習算法應用到油氣領域[11-13]。而針對氣井產(chǎn)能預測的數(shù)據(jù)驅(qū)動算法是其中一種重要應用場景[14]。數(shù)據(jù)驅(qū)動方法能夠避免物理機理分析方法構(gòu)建的復雜性和多解性[15]。具體而言，單井產(chǎn)能預測問題的輸入和預測對象均具有時間序列維度上連續(xù)性和自相關性。然而，地質(zhì)和生產(chǎn)參數(shù)與產(chǎn)能隨時間的變化具有強非線性關系[16]。針對這一問題，一些學者應用支持向量機[16-17]、粒子群[18]、BP神經(jīng)網(wǎng)絡[19-20](Back Propagation Neural Network)、循環(huán)神經(jīng)網(wǎng)絡[21]和LSTM神經(jīng)網(wǎng)絡[22-23](Long-Short Term Memory Neural Network)等算法的變形或耦合模型構(gòu)建產(chǎn)能預測模型，以更好地捕獲地質(zhì)和生產(chǎn)兩方面中多個控制參數(shù)(如井斜、垂深、孔隙度、排量、射孔簇數(shù)、支撐劑等)對生產(chǎn)曲線的非線性關系，從而提高產(chǎn)能預測的準確率。這些機器學習算法能夠簡化產(chǎn)能預測模型的構(gòu)建和動態(tài)求解速度，但在產(chǎn)能預測模型優(yōu)選、小樣本訓練、非結(jié)構(gòu)化數(shù)據(jù)處理和主控因素分析等方面仍存在挑戰(zhàn)。首先，產(chǎn)能預測的關鍵預測對象是氣井正式投產(chǎn)后的未來產(chǎn)量動態(tài)變化，其影響因素不僅包括地質(zhì)和生產(chǎn)過程中與時間無關的靜態(tài)參數(shù)，還包括氣井前期生產(chǎn)的產(chǎn)能時序數(shù)據(jù)。如何在時序序列預測模型中考慮靜態(tài)參數(shù)是產(chǎn)能預測神經(jīng)網(wǎng)絡模型構(gòu)建的關鍵。此外，氣井產(chǎn)能預測模型的現(xiàn)場數(shù)據(jù)樣本較少，且一些樣本中存在異常產(chǎn)能趨勢，這會造成模型訓練的過擬合和泛化能力差等問題。針對以上問題，如何對神經(jīng)網(wǎng)絡模型結(jié)構(gòu)和預測流程進行適應性修正是目前亟需解決的問題。

本文基于LSTM和DNN(Deep Neural Network)神經(jīng)網(wǎng)絡，建立了擬合函數(shù)—神經(jīng)網(wǎng)絡協(xié)同的頁巖氣井動態(tài)產(chǎn)能預測模型。首先，針對非結(jié)構(gòu)化數(shù)據(jù)，本文利用維度擴展的方法表征了靜態(tài)數(shù)據(jù)的時間不變性，并將前期日產(chǎn)氣量、平均套管壓力共同組成的二維時序數(shù)據(jù)與用液強度、加砂強度、總含氣量、脆性礦物含量等靜態(tài)產(chǎn)能控制參數(shù)混合構(gòu)建數(shù)據(jù)集，以實現(xiàn)時序—非時序混合數(shù)據(jù)的時間序列預測。其次，本文將傳統(tǒng)產(chǎn)能遞減模型作為LSTM神經(jīng)網(wǎng)絡輸入層的“弱物理約束”，即在特征工程階段通過產(chǎn)能遞減模型的擬合函數(shù)對所有準備訓練的井樣本數(shù)據(jù)進行預篩選。其中，Arps產(chǎn)能遞減微分方程是Arps[9,24]提出的基于概率統(tǒng)計的產(chǎn)能預測模型，陳元千和郝明強[25]在此基礎上推導出Arps的指數(shù)遞減、雙曲遞減和調(diào)和遞減等3種不同遞減系數(shù)下的產(chǎn)能模型。本文基于Arps的3類遞減擬合函數(shù)，通過謝軍等人[26]提出的篩選法，以最小均方誤差（mean squared error，MSE)為標準自動優(yōu)選遞減模型，對我國某頁巖區(qū)塊中的各單井產(chǎn)能數(shù)據(jù)進行遞減曲線擬合，去除不符合產(chǎn)能遞減規(guī)律的無效樣本。同時，將實際工況下單日生產(chǎn)時間與產(chǎn)量的比例關系作為DNN神經(jīng)網(wǎng)絡輸出層的“強物理約束”，即在神經(jīng)網(wǎng)絡的最后一個全連接層后對輸出結(jié)果按實際單日生產(chǎn)時間進行縮放，以避免實際工況下由于臨時停泵等人為因素造成的產(chǎn)能曲線異常點對模型反向優(yōu)化過程的影響。基于以上兩類“物理約束”， 本文模型既能捕獲產(chǎn)能遞減的共性規(guī)律，也能避免人為因素造成的特征干擾，解決了模型的無物理規(guī)律、過擬合的問題，從而保證了預測結(jié)果的穩(wěn)定性。

最后，對篩選后的頁巖氣井的動態(tài)產(chǎn)能預測進行k折(k-fold)交叉驗證，并分別討論了神經(jīng)網(wǎng)絡模型參數(shù)、產(chǎn)能控制參數(shù)和時間步長等對于本文模型誤差的影響。結(jié)果顯示，LSTM+DNN神經(jīng)網(wǎng)絡可以通過用液強度、加砂強度、總含氣量、脆性礦物含量等靜態(tài)產(chǎn)能控制參數(shù)，前期生產(chǎn)、壓力曲線和單日實際生產(chǎn)時間序列較快速準確地捕捉的后期生產(chǎn)特征。此外，通過擬合函數(shù)和神經(jīng)網(wǎng)絡的協(xié)同，在不增加樣本規(guī)模的條件下模型能較準確和穩(wěn)定地預測后期產(chǎn)能遞減趨勢。本文模型對于頁巖氣動態(tài)產(chǎn)能預測具有更好的預測能力，對老井壓裂效果評價和新井生產(chǎn)參數(shù)優(yōu)化具有一定指導意義。

1 方法與模型

1.1 LSTM神經(jīng)網(wǎng)絡原理

長短期記憶神經(jīng)網(wǎng)絡(LSTM)主體結(jié)構(gòu)類似于RNN(Recurrent Neural Network)的鏈狀重復網(wǎng)絡結(jié)構(gòu)，主要區(qū)別在于將RNN模型中隱藏層中的神經(jīng)元替換為LSTM特有的結(jié)構(gòu)單元。其典型的結(jié)構(gòu)單元(見圖1)包括“遺忘門”(forget gate)、“輸入門”(input gate)、“輸出門”(output gate)[27]。

圖1 LSTM網(wǎng)絡結(jié)構(gòu)單元[28]Fig.1 LSTM network structure unit[28]

基于以上3個組成部分，LSTM網(wǎng)絡結(jié)構(gòu)單元典型的前向計算流程如下[27-29]：

式中，ft為“遺忘門”的輸出值(0～1間的數(shù)字)，決定了上一步處理器狀態(tài)(cell state)應被繼續(xù)傳遞的部分；it為“輸入門”的輸出值，決定了tanh類激活函數(shù)計算結(jié)果中應被保留的部分；ct為tanh類激活函數(shù)的計算結(jié)果，表征處理器狀態(tài)的值；ot為“輸出門”的輸出值；ht為整個隱藏層的輸出值；W表示各單元之間的權(quán)重系數(shù)矩陣；b表示各單元對應的偏置項；σ表示Sigmoid激活函數(shù)。

1.2 基于LSTM+DNN的動態(tài)產(chǎn)能預測模型

動態(tài)產(chǎn)能預測模型基于地質(zhì)及工程等靜態(tài)參數(shù)，產(chǎn)能、平均套管壓力等時序參數(shù)和單日實際生產(chǎn)時間等強約束控制參數(shù)共同構(gòu)建。現(xiàn)場數(shù)據(jù)包括50口頁巖氣井。其中，實測遞減階段的產(chǎn)能數(shù)據(jù)滿足模型構(gòu)建所需最小時間序列的井樣本共24口。整理出供優(yōu)選的地質(zhì)參數(shù)8個(楊氏模量、總有機碳含量、最大水平主應力、最小水平主應力、總含氣量、孔隙度、泊松比和脆性礦物含量)、工程參數(shù)6個(用液強度、加砂強度、平均泵壓、平均排量、段長和簇間距)。結(jié)合灰色關聯(lián)法和熵權(quán)法，確定各地質(zhì)、工程參數(shù)與產(chǎn)能的相關度[30]。為確保模型預測的穩(wěn)定性，從地質(zhì)、工程參數(shù)中各選取與產(chǎn)能相關度最高的前2個參數(shù)作為靜態(tài)產(chǎn)能控制參數(shù)，即用液強度、加砂強度、總含氣量、脆性礦物含量。

由于靜態(tài)產(chǎn)能控制參數(shù)無法直接和生產(chǎn)數(shù)據(jù)共同構(gòu)建時間序列數(shù)據(jù)集，因此需要進行維度擴展處理。具體而言，模型訓練包括多口井的數(shù)據(jù)，其中每口井具有與時間相關的產(chǎn)能、平均套管壓力數(shù)據(jù)和特定且唯一的一組時間無關的靜態(tài)產(chǎn)能控制參數(shù)。為了同時訓練并提取產(chǎn)能控制參數(shù)和前期產(chǎn)能、平均套管壓力數(shù)據(jù)對于后期產(chǎn)能數(shù)據(jù)的非線性規(guī)律，將每個時間無關的產(chǎn)能控制參數(shù)視為在該井后期產(chǎn)能曲線范圍內(nèi)與時間相關，并重復該范圍內(nèi)的靜態(tài)控制參數(shù)，擴展到后期產(chǎn)能曲線的同一時間維度。當后期產(chǎn)能曲線在時間維度上的每個時間點具有對應的一組產(chǎn)能控制參數(shù)值，則可將所有井前期產(chǎn)能、平均套管壓力數(shù)據(jù)和后期產(chǎn)能控制參數(shù)(包括單日實際生產(chǎn)時間)作為輸入特征向量，后期產(chǎn)能數(shù)據(jù)作為輸出特征向量，從而生成非結(jié)構(gòu)化的高維時間序列數(shù)據(jù)集。最后，基于LSTM和DNN神經(jīng)網(wǎng)絡，設計了多變量動態(tài)產(chǎn)能預測模型(如圖2)。模型訓練和迭代過程包括：(1)對產(chǎn)能樣本進行特征篩選，并構(gòu)建非結(jié)構(gòu)化的多變量時間序列數(shù)據(jù)集；(2)標準化數(shù)據(jù)集，劃分訓練集和測試集；(3)基于LSTM和DNN神經(jīng)網(wǎng)絡前向計算方法計算模型輸出值；(4)基于網(wǎng)絡層級和時間反向傳播，計算模型輸出值和實際值的誤差項；(5)計算各對應權(quán)重的梯度；(6)基于梯度的優(yōu)化算法更新權(quán)重；(7)重復迭代，確定最優(yōu)的產(chǎn)能預測結(jié)果，并將結(jié)果反標準化。

圖2 LSTM產(chǎn)能預測模型結(jié)構(gòu)Fig.2 LSTM productivity prediction model structure

產(chǎn)能模型包含6個產(chǎn)能控制參數(shù)(平均套管壓力、用液強度、加砂強度、總含氣量、脆性礦物含量和單日實際生產(chǎn)時間)，預實現(xiàn)通過某井前n個步長的產(chǎn)能數(shù)據(jù)預測后m個步長的產(chǎn)能數(shù)據(jù)。其中，模型主要設計為2個LSTM層和3層全連接層，分別通過3個輸入接口傳入所有產(chǎn)能控制參數(shù)和前期產(chǎn)能時序數(shù)據(jù)。模型對數(shù)據(jù)本身量級非常敏感，因此輸入前需利用min-max標準化將所有數(shù)據(jù)映射到0～1之間，以消除參數(shù)之間的量綱影響。具體而言，首先，針對模型中前2個LSTM層，主要用于捕獲產(chǎn)能遞減趨勢特征，需于第1個LSTM層輸入由前期產(chǎn)能時序數(shù)據(jù)和對應平均套管壓力時序數(shù)據(jù)組成的二維特征向量，即

其中Qn為第n時刻(步)的產(chǎn)能數(shù)據(jù)，x1,n為第n時刻(步)的平均套管壓力，X1表示第一組輸入特征向量。

前2個LSTM層將輸出一組一維的中間變量，其長度與預測生產(chǎn)曲線的時間序列步長(m)一致。同時，將用液強度、加砂強度、總含氣量、脆性礦物含量維度擴展為預測生產(chǎn)曲線的時間序列步長(m)，并與LSTM層輸出的中間變量共同組成一組新的五維特征向量，即

其中，x2,n m+為LSTM層輸出的中間變量，x3,n m+～x6,n m+分別為維度擴展后的用液強度、加砂強度、總含氣量、脆性礦物含量數(shù)據(jù)，X2表示第二組輸入特征向量。

通過3個全連接層后將輸出得到第n時刻至第n+m時刻間的產(chǎn)能數(shù)據(jù)。然后，輸入同時間段內(nèi)各個時刻的單日實際生產(chǎn)時間，作為第三組輸入特征向量，即

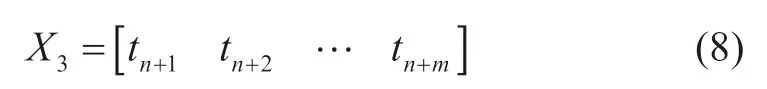
基于單日實際生產(chǎn)時間與對應單日產(chǎn)能數(shù)據(jù)的等比例關系，修正3個全連接層輸出的產(chǎn)能，修正公式如下

其中，Qn m+和Qn m′+分別為修正前后的無因次產(chǎn)能預測值，需要通過反標準化確定最終的預測產(chǎn)量。

根據(jù)單井產(chǎn)能預測的實際條件，在訓練過程中需要以井為單位分批構(gòu)建時間序列進行模型訓練，每口井重組10個樣本(當單井實測時間序列不足劃分10個樣本時，取其能夠劃分的最多樣本數(shù))。其中，從各井產(chǎn)能遞減階段的起始位置開始，向后取點作為樣本時間序列的初始時刻T，并取T～T n+時刻的生產(chǎn)曲線作為已知時間序列，T n++1～T n m++時刻的生產(chǎn)曲線作為預測目標。

2 結(jié)果與討論

2.1 基于Arps產(chǎn)能遞減模型的特征篩選

對于動態(tài)產(chǎn)能預測模型，當訓練集的大量井樣本中出現(xiàn)過多異常的無效樣本，會造成神經(jīng)網(wǎng)絡特征提取過程中計算出錯誤的權(quán)重，反而會降低模型預測的精度。因此，在LSTM動態(tài)產(chǎn)能預測模型訓練前需要進行一定預處理。除了對數(shù)據(jù)標準化，還需要篩選去除產(chǎn)量曲線明顯異常的樣本，以提高動態(tài)產(chǎn)能預測模型的特征提取的準確率。針對我國某頁巖區(qū)塊的單井產(chǎn)能曲線預測進行特征篩選。篩選對象共包含24口同區(qū)塊頁巖氣井的真實產(chǎn)能數(shù)據(jù)。本文以Arps產(chǎn)能遞減模型的擬合曲線作為評判標準篩選出12口符合產(chǎn)能遞減規(guī)律的井樣本(圖3)。其中，Arps產(chǎn)能遞減模型的一般微分方程表示為[25]

圖3 基于Arps產(chǎn)能遞減模型的訓練及測試井樣本篩選Fig.3 Training and test well sample selection based on Arps productivity model

其中，q為產(chǎn)量(104m3/天)，t為時間(天)，n為遞減指數(shù)，Di為初始產(chǎn)量(104m3/天)。

根據(jù)遞減指數(shù)n的不同，Arps微分方程可進一步表示為

分別利用3種模型擬合遞減曲線，并比較不同擬合曲線的MSE，以最小MSE為標準自動優(yōu)選遞減模型擬合曲線。

基于特征篩選后的井樣本，以天為單位對各井日產(chǎn)氣量數(shù)據(jù)進行時間序列化，并通過k-fold交叉驗證評價模型精度。具體而言，輪流將每口井作為測試集、其他11口井作為訓練集進行模型訓練和產(chǎn)能預測，并計算對應的MSE，最后將12次測試得到的均方誤差取平均，獲得最終用于評價模型精度的誤差值。當誤差值越大，表明模型預測精度越低。

以k-fold交叉驗證所得的平均誤差值為基礎，通過對神經(jīng)網(wǎng)絡模型參數(shù)的優(yōu)選確定最優(yōu)的動態(tài)產(chǎn)能預測模型設計方案，最后討論了靜態(tài)產(chǎn)能控制參數(shù)和時間步長對模型精度的影響。

2.2 神經(jīng)網(wǎng)絡模型參數(shù)的影響規(guī)律

神經(jīng)網(wǎng)絡模型參數(shù)包括激活函數(shù)和梯度優(yōu)化函數(shù)等。激活函數(shù)決定了神經(jīng)網(wǎng)絡前向計算時各層神經(jīng)元向下一層傳遞的輸出。除了linear激活函數(shù)，其他激活函數(shù)均為非線性函數(shù)，能夠強化網(wǎng)絡的非線性學習能力。梯度優(yōu)化函數(shù)是神經(jīng)網(wǎng)絡在反向傳播計算誤差項時引導損失函數(shù)梯度下降的優(yōu)化函數(shù)，即令損失函數(shù)的參數(shù)沿某一方向更新，使損失函數(shù)值逼近全局最小。梯度優(yōu)化函數(shù)決定了損失函數(shù)的優(yōu)化方向和步長。因此，針對本文模型優(yōu)選激活函數(shù)和梯度優(yōu)化函數(shù)能夠提高模型的收斂速度和預測精度。

對于模型中LSTM層的2層輸出的激活函數(shù)，分別取ELU、SELU、tanh、Sigmoid和linear激活函數(shù)進行交叉驗證實驗，確定各激活函數(shù)及其組合下的模型精度如表1所示。結(jié)果顯示，ELU、tanh和Sigmoid函數(shù)的模型預測效果相對較好。綜合考慮各函數(shù)條件下的模型對于各井的預測誤差和平均誤差，優(yōu)選Sigmoid函數(shù)作為模型的激活函數(shù)。其中Sigmoid函數(shù)表示為

表1 不同激活函數(shù)下的模型預測精度Table 1 Prediction accuracy of models with different activation functions

對于模型的梯度優(yōu)化函數(shù)。令LSTM層的激活函數(shù)為ELU和tanh函數(shù)，分別取梯度優(yōu)化函數(shù)為SGD[31]、RMSprop[32]、Adagrad[33]、Adadelta、Adam、Adamax和Nadam[34]進行交叉驗證實驗，確定各梯度優(yōu)化函數(shù)下的模型誤差如表2所示。結(jié)果顯示，Nadam函數(shù)的模型預測效果最好。其梯度計算公式如下[34]

表2 不同梯度優(yōu)化函數(shù)下的模型的誤差對比Table 2 Error comparison of models with different gradient optimization functions

式中，gt為平均梯度，θt為目標更新參數(shù)，nt為梯度的二階矩估計值，mt為梯度一階矩，∈為初始常數(shù)，α為動量系數(shù)。

最后，以Sigmoid作為激活函數(shù)，Nadam作為梯度優(yōu)化函數(shù)訓練動態(tài)產(chǎn)能預測模型，預測結(jié)果見圖4。交叉驗證結(jié)果顯示，基于Sigmoid激活函數(shù)和Nadam梯度優(yōu)化函數(shù)的動態(tài)產(chǎn)能預測模型的平均誤差為2.0001，其中大部分井具有較好的預測效果。對于實際對于同一區(qū)塊的具有相似產(chǎn)能遞減規(guī)律的氣井，通過對多個老井的訓練，得到的模型能夠基于新井前期部分產(chǎn)能曲線和用液強度、加砂強度、總含氣量、脆性礦物含量等產(chǎn)能控制參數(shù)共同預測未來產(chǎn)能遞減曲線。神經(jīng)網(wǎng)絡模型結(jié)構(gòu)包含單日實際生產(chǎn)時間的強約束，有效降低了實際工況下大量異常產(chǎn)能數(shù)據(jù)點對產(chǎn)能趨勢的影響。

2.3 靜態(tài)產(chǎn)能控制參數(shù)的影響規(guī)律

本小節(jié)主要分析了靜態(tài)產(chǎn)能控制參數(shù)對產(chǎn)能預測模型的影響。首先，保持神經(jīng)網(wǎng)絡模型結(jié)構(gòu)不變，去除所有靜態(tài)參數(shù)的輸入接口，即第二組輸入特征向量X2變?yōu)榍?個LSTM層輸出的一維中間變量。以2.2中確定的神經(jīng)網(wǎng)絡超參數(shù)重新訓練模型，并與考慮靜態(tài)控制參數(shù)的原模型預測結(jié)果進行對比(圖5)。

結(jié)果顯示，不含靜態(tài)產(chǎn)能控制參數(shù)(用液強度、加砂強度、總含氣量和脆性礦物含量)的模型預測結(jié)果整體偏高。對于同一口井，其靜態(tài)產(chǎn)能控制參數(shù)不變。當通過2層LSTM神經(jīng)網(wǎng)絡確定后期產(chǎn)能趨勢預測結(jié)果后，靜態(tài)產(chǎn)能控制參數(shù)主要通過DNN神經(jīng)網(wǎng)絡對后期各天的產(chǎn)能預測值進行校正，并修正對應模型權(quán)重。極端條件下，當產(chǎn)能控制參數(shù)數(shù)值變化對產(chǎn)能影響較大，其校正后的產(chǎn)能預測值將偏離LSTM確定的整體產(chǎn)能趨勢。例如單日實際生產(chǎn)時間與單日產(chǎn)能具有強烈的正比例關系，圖5中第90～100天內(nèi)單日實際生產(chǎn)時間由24小時驟減為9小時，其產(chǎn)能預測值同樣遠小于趨勢預測結(jié)果。固定其他產(chǎn)能參數(shù)不變，將10井的加砂強度分別設置為1.415、1.978和2.542(所有樣本的加砂強度范圍為1.415～2.542 t/m)，設置三組實驗(圖6)。結(jié)果顯示，隨著加砂強度的增加，后期的平均日產(chǎn)氣量同樣增加。

圖5 考慮與不考慮靜態(tài)產(chǎn)能控制參數(shù)的10井產(chǎn)能預測結(jié)果Fig.5 Productivity prediction results for well-10 with and without static productivity control parameters

圖6 不同加砂強度條件下的10井平均產(chǎn)能預測結(jié)果Fig.6 Average productivity prediction results of well-10 with different sand addition strength conditions

2.4 輸入時間步長和預測時間步長的影響規(guī)律

本小節(jié)分別分析了輸入時間步長和預測時間步長對動態(tài)產(chǎn)能預測模型預測精度的影響。其中預測模型參數(shù)設置由2.2小節(jié)的激活函數(shù)和優(yōu)化函數(shù)優(yōu)選結(jié)果確定。首先固定預測時間步長為90天，分別設置輸入時間步長為40，50，60和70天，對12口井進行k-fold交叉驗證，各輸入時間步長條件下的各井預測的平均誤差結(jié)果如表3所示，其中2井的預測結(jié)果如圖7所示。

圖7 輸入時間步長分別為40，50，60和70天的2井產(chǎn)能預測結(jié)果Fig.7 well-2 productivity prediction results for input time steps of 40, 50, 60 and 70 days, respectively

表3 輸入時間步長為40，50，60和70天的5井產(chǎn)能預測模型的誤差對比Table 3 Error comparison of productivity prediction models with input time steps of 40，50，60和70 days

固定輸入時間步長為50天，分別設置預測時間步長為30、50、70和90天，對12口井進行k-fold交叉驗證，各預測時間步長條件下的各井預測的平均誤差結(jié)果如表4所示，其中4井的預測結(jié)果如圖8所示。輸入時間步長為50天，設置預測時間輸出步長為200天，其中2井的預測結(jié)果如圖9所示。

圖8 預測時間步長分別為30、50、70和90天的4井產(chǎn)能預測結(jié)果Fig.8 Well-4 productivity prediction results for forecast time steps of 30, 50, 70 and 90 days, respectively

圖9 預測時間步長200的2井產(chǎn)能預測結(jié)果Fig.9 Well-2 productivity prediction results for forecast time steps of 200

表4 預測時間步長為30、50、70和90天的產(chǎn)能模型的誤差對比Table 4 Error comparison of productivity prediction models with forecast time steps of 30, 50, 70 and 90 days

結(jié)果顯示，在40～70天范圍內(nèi)，輸入時間步長對產(chǎn)能預測精度具有較大影響。當已知的時間序列數(shù)據(jù)越多，模型精度反而越低。其中，前期異常衰減的產(chǎn)能數(shù)據(jù)點對預測結(jié)果影響較大。模型中單日實際生產(chǎn)時間主要約束未來產(chǎn)能遞減趨勢中的異常衰減點。隨著輸入時間步長的增加，各井前期存在的衰減點變多，且避開了單日實際生產(chǎn)時間的強約束，削弱了產(chǎn)能趨勢特征。其次，預測時間步長的增加并沒有明顯降低模型預測的精度。由于數(shù)據(jù)預處理過程對產(chǎn)能曲線樣本進行了特征篩選，各樣本的產(chǎn)能曲線均滿足一般遞減規(guī)律。基于序列到序列的LSTM神經(jīng)網(wǎng)絡，能夠有效建立前期產(chǎn)能、平均套管壓力曲線時間序列和后期遞減曲線時間序列的特征關系。同時，通過多個靜態(tài)產(chǎn)能控制參數(shù)的權(quán)重校正和單日時間生產(chǎn)時間的強約束，進一步提高了后期產(chǎn)能曲線的局部預測精度。最后，通過2井的200天產(chǎn)能預測結(jié)果，進一步說明動態(tài)產(chǎn)能預測模型對于更長期產(chǎn)能曲線預測具有較好的適用性。

3 結(jié)論

基于LSTM和DNN神經(jīng)網(wǎng)絡，本文建立了擬合函數(shù)—神經(jīng)網(wǎng)絡協(xié)同的動態(tài)產(chǎn)能預測模型。模型能夠有效捕捉產(chǎn)能曲線在時間維度和地質(zhì)及工程維度上的非線性規(guī)律。針對某頁巖區(qū)塊的篩選后的12口井，基于k折交叉驗證分析了神經(jīng)網(wǎng)絡模型參數(shù)、靜態(tài)產(chǎn)能控制參數(shù)、輸入時間步長和預測時間步長對模型預測精度的影響。結(jié)論如下：1)通過LSTM和DNN神經(jīng)網(wǎng)絡的耦合，可實現(xiàn)多個時序—非時序產(chǎn)能控制參數(shù)對后期產(chǎn)能曲線的聯(lián)合約束；2)在數(shù)據(jù)預處理過程中通過擬合函數(shù)對現(xiàn)場數(shù)據(jù)的規(guī)律性判斷，預篩選符合產(chǎn)能遞減趨勢的樣本作為模型訓練集，以間接加入含產(chǎn)能遞減規(guī)律的弱物理約束，可在不增加樣本規(guī)模的條件下能夠有效提高模型訓練的精度；3)基于實際工況下單日生產(chǎn)時間與產(chǎn)量的強相關性，于神經(jīng)網(wǎng)絡模型內(nèi)部加入產(chǎn)能等比例縮放的強物理約束，能夠有效提高模型的預測精度和局部穩(wěn)定性；4)激活函數(shù)、梯度優(yōu)化函數(shù)分別為Sigmoid函數(shù)和Nadam函數(shù)時模型預測誤差值為2.0001，預測效果最好；5)預測時間步長的增加并沒有明顯降低模型預測的精度，LSTM神經(jīng)網(wǎng)絡能夠有效捕捉長期的時間序列信息。綜上，本文模型考慮了擬合模型的特征篩選，結(jié)合單日生產(chǎn)時間的強物理約束，并針對現(xiàn)場產(chǎn)能數(shù)據(jù)進行訓練和預測，能夠較好適應不同特征的產(chǎn)能曲線樣本，并獲取對應的產(chǎn)能遞減規(guī)律，可以一定程度上輔助頁巖氣井未來產(chǎn)能曲線預測。