基于模糊神經網絡的巖溶發育預測研究
盛建龍,喬 宇,俞棟華,王 平,張彥文
(1.武漢科技大學資源與環境工程學院,湖北 武漢 430081;2.湖北省工業建筑集團有限公司,湖北 武漢 430076)
0 引 言
巖溶(Karst)地質成因復雜、構造特殊,在工程活動中導致了諸多損失。因此,研究巖溶發育,根據發育規律對巖溶發育程度進行評估及預測,可在巖溶環境致災前做出及時處理,減少巖溶災害帶來的損失,具有重要的工程意義[1-3]。一直以來,很多學者不斷進行巖溶相關工程問題評價的探索,如研究巖溶塌陷預測問題時使用了模糊綜合評價法[4- 6],研究巖溶水位與降水量、開采量之間的關系問題時使用了灰色關聯度法[7],研究巖溶隧道突水評估問題時使用層次分析法、區間屬性數學法[8]等。對于巖溶發育預測問題,目前有使用層次分析法[9]、模糊評價法[10]等的半經驗模型,有使用統計數學方法[11-12],也有使用層次分析法和貝葉斯網絡法相結合的模型[13]。但是,因實際工程問題具有復雜性、不確定性和非線性等特點,在使用傳統方法時,過程較繁雜且帶有較大的主觀性。
神經網絡模型能夠根據訓練樣本自動調整結構參數,改變映射關系,具有較強的自適應性,可實現各種非線性映射,較好地解決傳統方法中較大的主觀性,提高了評估精確性,簡化了解決過程。當前,神經網絡模型在巖溶相關工程問題中有較多的應用。如BP神經網絡被使用在巖溶塌陷預測模型[14-18],巖溶隧道突水風險預測模型[19],溶洞規模預測模型[20]等。但對于巖溶發育預測的神經網絡模型應用較少。為此,本文結合武漢市某工程區域,建立了模糊神經網絡模型預測巖溶發育情況,并與BP神經網絡模型做了效果對比。
1 模糊神經網絡原理
模糊神經網絡(FNN)是模糊理論與神經網絡相結合的一種理論。神經網絡彌補了模糊系統無法自學習、主觀性強的缺點,模糊系統彌補了神經網絡對知識提取和表達困難的缺點[21]。模糊神經網絡繼承了兩者的優點,彌補了各自的不足。
模糊神經網絡結構見圖1。輸入層為第1層,此層節點的個數為輸入變量的個數,將輸入值傳遞至下一層。模糊化層為第2層,該層實現輸入變量的模糊化,即隸屬度劃分,節點個數為各個輸入變量的模糊集合數之和。模糊規則計算層為第3層,該層可細分為求“與”層與求“或”層[21],其節點分別對應規則Ri的If部分和then部分,通過規則Ri的模糊推理,得到變量的各個模糊集合的隸屬度值。輸出層為第4層,即反模糊化層,該層將上一層輸出的隸屬度值進行清晰化,轉化為輸出變量的精確值。
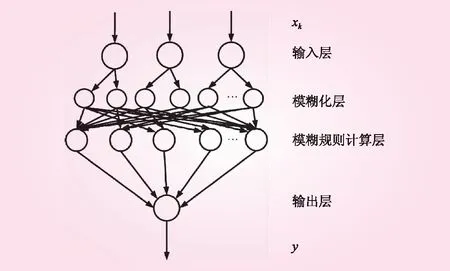
圖1 模糊神經網絡結構


(1)
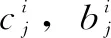
(2)
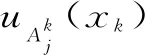
根據模糊計算結果計算模糊模型的輸出值,即
(3)
2 模型建立及應用
2.1 相關指標的確定
工程位于湖北省武漢市蔡甸區,總占地面積約32 614 m2,場區西側毗鄰高速公路,東側距離長江邊界約1.2 km,原始地貌單元為長江Ⅱ級階地湖泊和湖泊灘涂地帶,為廣袤的填湖區。武漢市軟土分布區,無全新活動斷層經過,基巖為二疊系泥巖、碳質泥巖及灰巖,下伏灰巖巖溶較為發育,基巖面起伏較大,巖溶裂隙發育。圖2為項目場區衛星位置。

圖2 項目場區衛星位置(圖中標注位置)
擬建場區地下水在勘察深度范圍內主要為賦存于上部填土層中的上層滯水和基巖中的基巖裂隙水和可溶巖中的巖溶裂隙水,上層滯水主要由地表水源、大氣降水補給,無統一的自由水面,水位及水量隨地表水源、大氣降水的影響而波動,反映了覆蓋層的滲透能力及地表水的影響能力,間接影響巖溶發育。基巖裂隙水主要賦存于各類泥巖中,主要補給來源為地層側向滲透,水量不大,可不考慮。巖溶裂隙水主要賦存于灰巖的裂隙中,主要補給來源為地層滲透,埋藏深,具承壓性。地下水對基巖的潛蝕、沖刷是巖溶發育的主要誘因,結合地下水位、地下水上下波動及基巖標高來考慮,取地下水位高程、基巖標高為評價指標。此外,灰巖作為典型碳酸鹽巖,是巖溶發育必不可少的條件,取基巖是否為碳酸鹽巖為評價指標。
覆蓋層過厚一般會存在多層隔水層或過厚隔水層不利于地下水徑流交換侵蝕作用,同時過厚覆蓋層形成較大垂向壓力,易致巖溶發育所產生土洞塌陷;而覆蓋層過薄則易受外界環境因素的影響,取覆蓋層厚度為評價指標。
根據勘察剖面圖可知,巖層組合可分為單層灰巖、單層泥巖加灰巖、雙層泥巖加灰巖3種類型。場區基巖為二疊系泥巖、碳質泥巖及灰巖。基巖分界線北側基巖為泥巖、碳質泥巖,南側基巖為灰巖。2種基巖呈不整合接觸,接觸地帶巖石破碎。同時,考慮巖性影響(碳酸鹽含量、顆粒大小、與水接觸作用面積等),取基巖層數為評價指標。
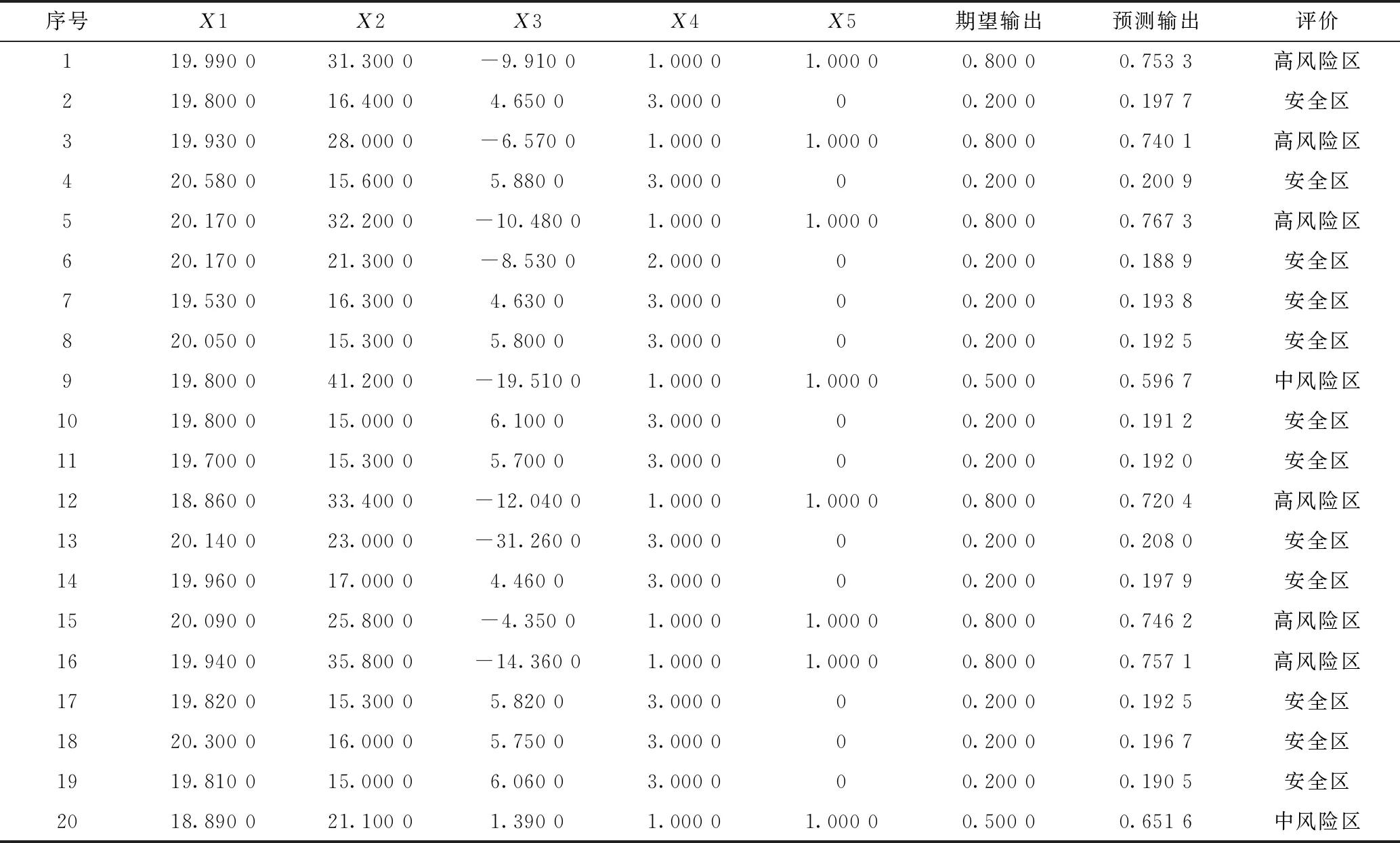
表1 訓練樣本及結果節選
綜上,選取地下水位高程(X1)、覆蓋層厚度(X2)、基巖標高(X3)、基巖層數(X4)、基巖是否為碳酸鹽巖(X5)等5個因子作為輸入參數。其中,基巖層數(X4),單層取1,雙層取2,多層取3。基巖是否為碳酸鹽巖(X5),是取1,否取0。輸出層對應評價指標,巖溶發育高風險區(勘察到溶洞和土洞)取0.8,中風險區(滿足發育條件,但未勘察到明顯現象)取0.5,安全區取0.2。輸入層個數為5個,隱含層根據2N+1原則取11,輸出層為1,因此,網絡結構為5-11-1。
2.2 訓練及預測
根據地質資料選取數據完整、有代表性的樣本81個,其中訓練樣本69個,測試樣本12個。在運算中,模型的模糊隸屬度函數中心和寬度均隨機賦值,導致每次運行后的結果可能不一樣,所以在訓練和預測時,采取隨機10組的結果求平均值的方法減少樣本誤差。圖3與圖4分別是第1組訓練樣本和節選的4組預測樣本的實際輸出、預測輸出和誤差對比。表1為節選的20個訓練樣本數據。表2為12個測試樣本的數據。
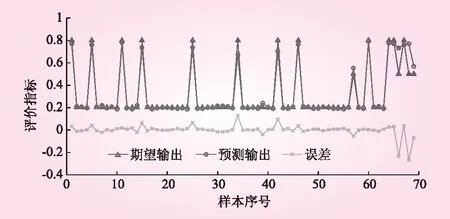
圖3 第1組訓練樣本實際輸出、預測輸出和誤差對比
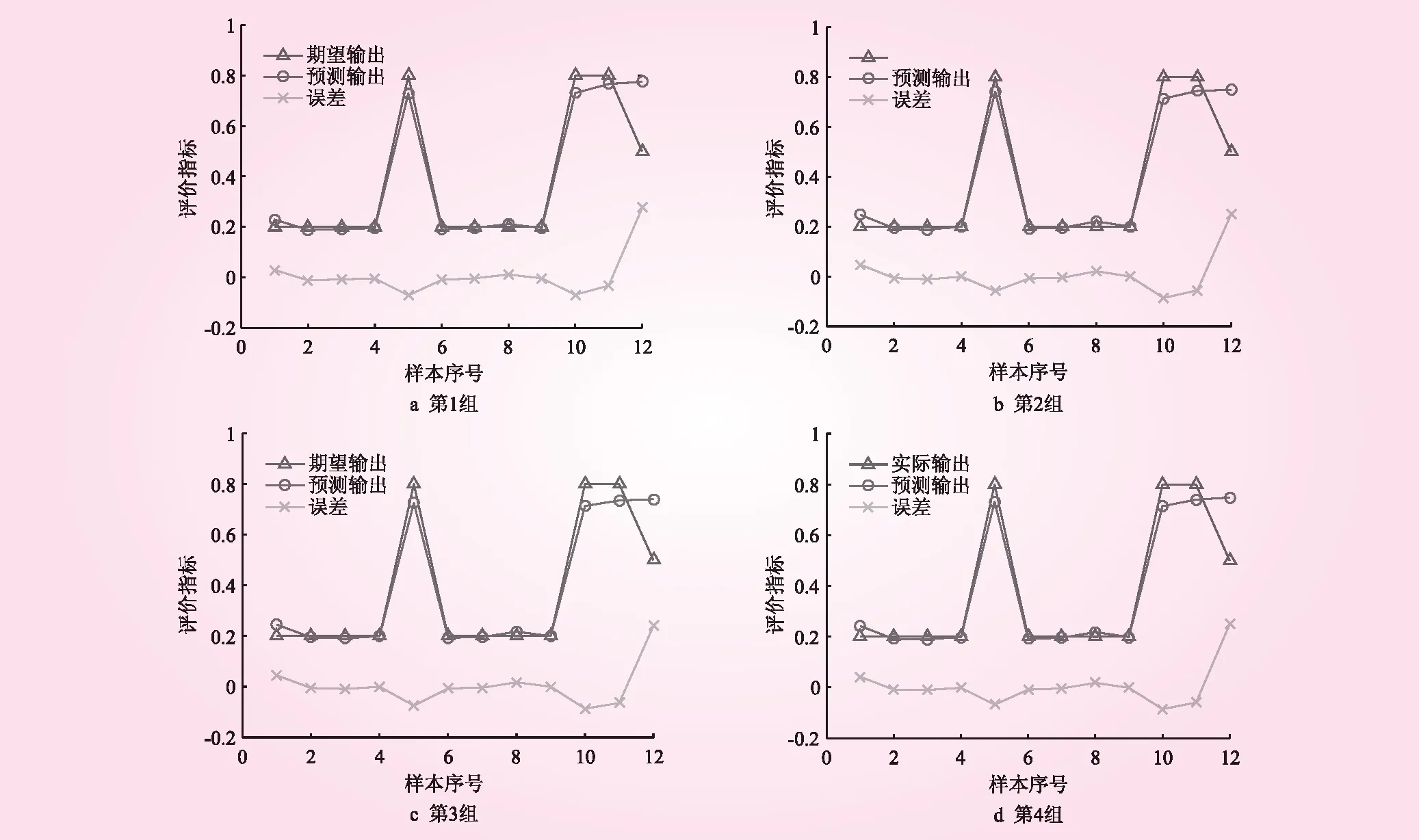
圖4 4組測試樣本中實際輸出、預測輸出和誤差對比
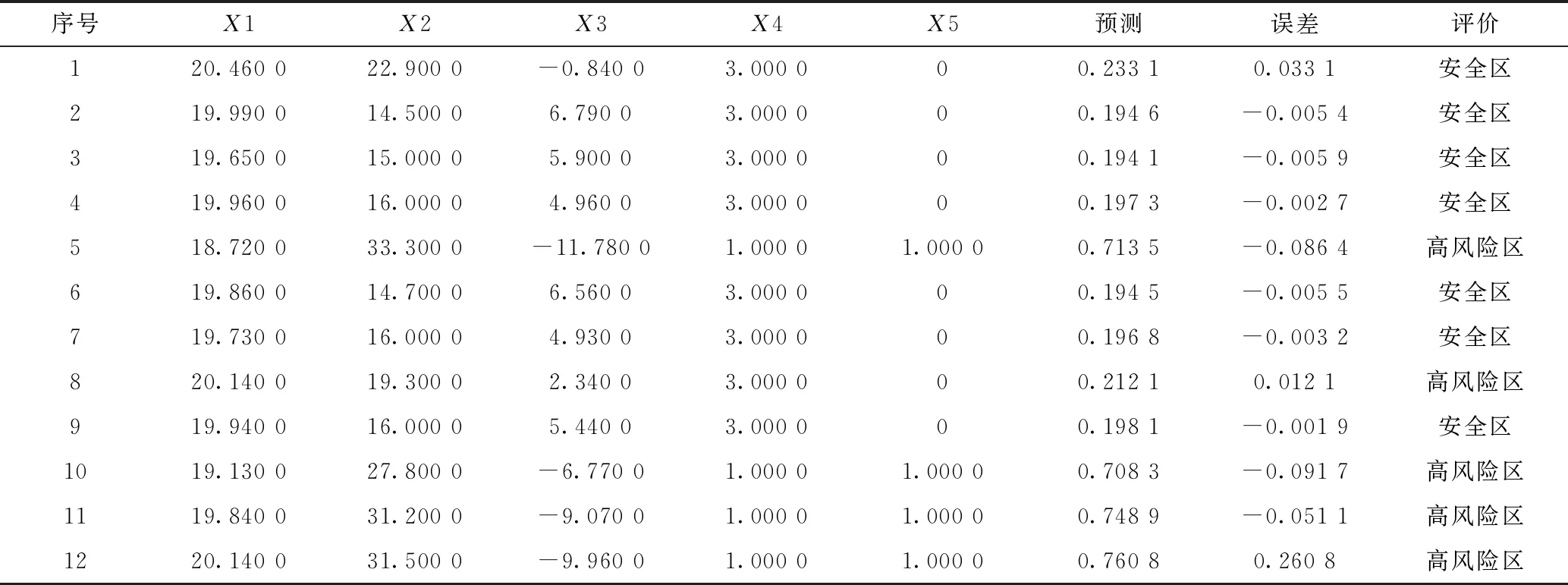
表2 預測結果
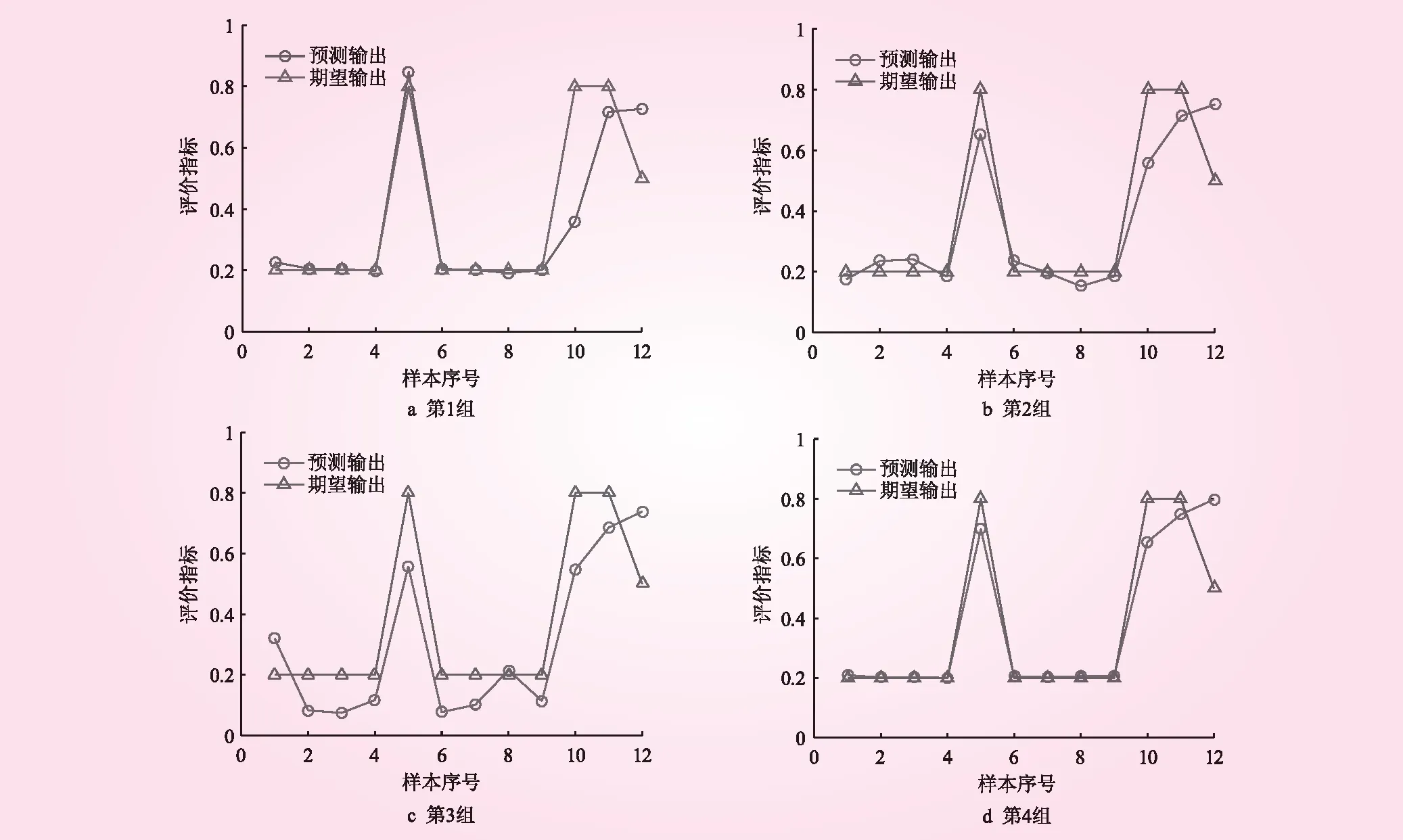
圖5 4組預測輸出與期望輸出對比
從圖4和表2可知,預測期望值與實際值存在一定的誤差,中風險區誤差較大。經計算,預測值的平均誤差為4.7%,在可接受的范圍內,說明該模型可以有效地進行巖溶發育的初步預測。
3 對比BP神經網絡模型
3.1 模型對比
預測樣本、測試樣本與模糊神經網絡模型相同,網絡結構為5-11-1,學習率為0.01,訓練次數為20 000 次,目標精度值為0.000 1,同樣采用隨機10組的結果求平均值的方法減少樣本誤差。圖5為節選的4組預測輸出與期望輸出對比。
BP神經網絡模型與模糊神經網絡模型預測輸出數據見表3。從表3可知,在高風險預測中,模糊神經網絡模型的相對誤差為-9.6%,BP神經網絡模型的相對誤差為-13.5%,在安全區預測中,兩者相對誤差分別為1.3%與3.6%。在中風險區預測中,2個模型呈現出較大且相近的誤差。與BP模型相比,模糊模型的預測曲線更加接近期望曲線,模糊神經網絡模型在高風險區和安全區的預測結果比BP神經網絡模型效果更好,精度更高,誤差滿足工程要求,且2種模型在中風險區預測效果相當。因此,與BP神經網絡相比,模糊神經網絡模型能夠更好地應用于解決巖溶發育初步預測的實際問題中。
3.2 誤差分析
支持向量機(SVM)是一個小樣本二分類模型,在分析誤差原因時,采用“一對多”的方法構建多個SVM模型進行分析。訓練結果顯示,除高風險與中風險構建的模型準確率較低外,其余的模型準確率都為100%,此結果驗證了2種神經網絡模型預測結果的可靠性。從2種神經網絡模型的輸出對比圖來看,中風險區的預測輸出逼近于高風險區的判斷指標,這也與高風險和中風險構建的SVM模型訓練結果吻合。因此,中風險區較大誤差的外在原因是由于模型將中風險區判斷為高風險區。
結合神經網絡模型對樣本數據的要求,認為其內在原因是由于中風險區樣本過少,并采用AUC指數證明此結論。AUC是受試者工作特征曲線(ROC曲線)下與坐標軸圍成的面積,可作為一種衡量預測模型優劣的指標,AUC越接近1,模型效果越好。因中風險樣本有限,所以用減少高風險樣本數量的方式,代替增加中風險樣本的效果。將高風險樣本數量減少到與中風險相同,建立SVM模型,進行AUC評價。為減少數據帶來的誤差,隨機取10組的評價結果進行平均,表4為AUC評價結果。從表4可知,與初始樣本相比,當兩類樣本數量相同時,模型預測效果顯著提升,證實了中風險區較大誤差的內在原因是由于其樣本過少。綜上認為,中風險區較大誤差產生的主要原因可能有2點:①工程條件中,中風險區樣本數量過少;②工程勘探中,試驗孔未能捕捉到巖溶初期發育情況,導致了期望輸出指數的確定有偏差。
4 結 語
本文基于模糊神經網絡,對巖溶發育預測進行了研究,得出以下結論:
(1)采用模糊神經網絡模型,確定5種輸入參數,得到的預測結果滿足工程需要,為預測巖溶發育提供了思路。

表4 AUC評價結果
(2)從模糊神經網絡模型與BP神經網絡模型在同一工程中應用對比來看,模糊神經網絡模型在精度上優于BP神經網絡模型,效果更好,可為巖溶初步預測工作提供依據,在實際工程中具有一定的使用價值。
(3)根據神經網絡的特點,在使用模型時,應盡量提供更多更具代表性的樣本,使模型得到充分的學習,以發揮更好的效果。

