跨音速流中壁板流固耦合效應(yīng)的形態(tài)演化分析

安效民，馮家悅，周 悅，孫 偉

(西北工業(yè)大學(xué)航天學(xué)院空天飛行技術(shù)研究所，西安 710072)

超音速飛行器的翼、身及重復(fù)使用火箭的箭體多采用輕質(zhì)薄壁加筋結(jié)構(gòu)，其一側(cè)直接承受氣動(dòng)載荷作用，另一側(cè)為腔體結(jié)構(gòu)。這種薄壁結(jié)構(gòu)在氣動(dòng)載荷作用下發(fā)生變形，導(dǎo)致外部流場的邊界發(fā)生改變，引起流場的結(jié)構(gòu)(如邊界層、激波等)和氣流參數(shù)(如速度、壓強(qiáng)等)的改變，使得作用在結(jié)構(gòu)上的氣動(dòng)載荷發(fā)生變化，進(jìn)而使結(jié)構(gòu)產(chǎn)生新的變形或者振動(dòng)。這種結(jié)構(gòu)彈性、氣動(dòng)載荷與慣性載荷間的相互耦合，會導(dǎo)致壁板氣動(dòng)彈性問題，出現(xiàn)不穩(wěn)定性現(xiàn)象[1-4]。

與傳統(tǒng)翼、舵等升力面構(gòu)型不同的是，薄壁結(jié)構(gòu)在跨音速流表現(xiàn)出了雙重的非線性流固耦合特征。一方面，壁板位移響應(yīng)通常與壁板厚度為相同量級，壁板面內(nèi)應(yīng)力存在，彎曲和拉伸之間會發(fā)生耦合，在周圍受約束(固支或簡支)條件下，其形變一般不會引發(fā)結(jié)構(gòu)的迅速破壞，但會引起結(jié)構(gòu)疲勞，表現(xiàn)為幾何非線性[5-7]。另一方面，壁板的響應(yīng)還受跨音速氣動(dòng)非線性的影響：① 由于壁板向上或向下的振蕩，會增強(qiáng)或減弱激波強(qiáng)度，并且使得激波前后運(yùn)動(dòng)，激波運(yùn)動(dòng)可能是連續(xù)的，也可能是間歇的，或者連續(xù)和間歇互相轉(zhuǎn)換，從而導(dǎo)致壁板復(fù)雜的響應(yīng)形態(tài)在相對較寬的動(dòng)壓范圍內(nèi)持續(xù)存在，而且會有多種形態(tài)之間的演化；② 激波與邊界層之間的干擾可能造成流動(dòng)分離，激波或分離渦的運(yùn)動(dòng)進(jìn)一步加劇了流動(dòng)的動(dòng)態(tài)非線性特征，使得壁板響應(yīng)更為復(fù)雜[8-10]，而且在跨音速區(qū)，粘性效應(yīng)本身對壁板響應(yīng)具有增穩(wěn)或失穩(wěn)作用[11-13]。

在這些跨音速流中強(qiáng)非線性因素的作用下：一方面壁板的穩(wěn)定邊界呈現(xiàn)出與流線型升力面構(gòu)型(如翼、舵部件等)相似的跨音速凹坑[5]；另一方面，在進(jìn)入到不穩(wěn)定區(qū)域后，壁板表現(xiàn)為多個(gè)不穩(wěn)定屈曲、極限環(huán)顫振或者更為復(fù)雜的振蕩行為，諸如周期性、擬周期、非周期和混沌等復(fù)雜響應(yīng)[14]。準(zhǔn)確預(yù)測和確定飛行器在跨音速下壁板結(jié)構(gòu)的穩(wěn)定邊界，并分析其在不穩(wěn)定域內(nèi)的形態(tài)演化規(guī)律，有助于揭示壁板各類復(fù)雜行為的誘發(fā)機(jī)理，尋求抑制甚至消除最嚴(yán)重形態(tài)響應(yīng)的方法，可有效降低飛行器的疲勞損傷，尤其是對于可重復(fù)使用火箭，其在上升段有較長時(shí)間飛行在跨音速及低超音速范圍，薄壁結(jié)構(gòu)受到氣動(dòng)載荷作用而產(chǎn)生的變形或振動(dòng)對結(jié)構(gòu)疲勞有著重要影響。

對于跨音速流固耦合效應(yīng)下壁板的非線性響應(yīng)問題，當(dāng)前無法建立統(tǒng)一的動(dòng)力學(xué)模型，傳統(tǒng)基于變分方法或其他離散化方法，將偏微分方程化為常微分方程組，進(jìn)而進(jìn)行特征值性態(tài)分析的應(yīng)用受限。DOWELL[15]提出了4 類壁板顫振分析理論，后來CHENG 和MEI[16]將其擴(kuò)充為6 類，他們都指出：在跨音速范圍內(nèi)，使用非線性結(jié)構(gòu)理論和求解流體的Euler/Navier-Stokes 方程是一種有效途徑。

DAVIS 等[8]聯(lián)立求解Euler 方程和非線性板的結(jié)構(gòu)方程，研究了M∞=0.8～2.5 范圍內(nèi)二維壁板的氣彈響應(yīng)，發(fā)現(xiàn)激波的出現(xiàn)會導(dǎo)致氣彈響應(yīng)出現(xiàn)發(fā)散和極限環(huán)等現(xiàn)象。GORDNIER 等[10]的研究中利用可壓N-S 方程求解壁板表面的氣動(dòng)力，并結(jié)合Von-Karman 理論，采用隱式迭代求解壁板響應(yīng)，分析了M∞=0.8下壁板的穩(wěn)定性，并解釋了粘性邊界層效應(yīng)對氣動(dòng)彈性穩(wěn)定性和顫振失穩(wěn)后形態(tài)的影響。HASHIMOTO 等[12]的研究則利用了耦合求解思路，將N-S 方程和Von-Karman 方程聯(lián)立起來，研究了邊界層效應(yīng)對壁板顫振的影響。ALDER[13]的研究中采用隱式有限體積法對N-S 方程進(jìn)行了求解，耦合考慮了幾何非線性的壁板有限元模型，分析了從高亞音速到低超音速下湍流邊界層對壁板系統(tǒng)穩(wěn)定邊界的影響。SHISHAEVA等[17-18]聯(lián)立ABAQUS 結(jié)構(gòu)求解器和Flowvision流場求解器，分析了二維壁板從高亞音速到低超音速階段的壁板響應(yīng)，指出隨馬赫數(shù)變化中，壁板會呈現(xiàn)為屈曲、動(dòng)態(tài)穩(wěn)定、單模態(tài)顫振、耦合顫振等多種響應(yīng)形式，并分析了加速、減速效應(yīng)下壁板的響應(yīng)形態(tài)變化。

國內(nèi)肖艷平等[19]基于一階活塞氣動(dòng)力理論，采用伽遼金法分析了邊界松弛對超音速氣流壁板顫振響應(yīng)的影響，結(jié)果表明：隨邊界約束的松弛，壁板可能產(chǎn)生顫振極限環(huán)振動(dòng)。吳志強(qiáng)等[20]通過數(shù)值計(jì)算龐加萊映射分岔的方法，討論了翼型在不可壓流中的極限環(huán)顫振隨氣流速度變化引起的分岔行為，給出了8 種典型的相圖和譜圖，并分析了閉軌分岔的誘因。鈕耀斌等[21]采用橢圓函數(shù)諧波平衡法研究分析了翼型的超音速非線性顫振問題，結(jié)果表明極限環(huán)振蕩臨界速度隨著彈性軸位置與翼弦中點(diǎn)距離的減小而不斷增大，且隨著重心位置與彈性軸距離的增大，極限環(huán)振蕩臨界速度存在一個(gè)極小值點(diǎn)。可以看出，這些非線性顫振大多關(guān)心超音速或低速流動(dòng)特點(diǎn)，氣動(dòng)力建模考慮了線性模型。朱世權(quán)等[22]基于CFD/CSD 單向流固耦合計(jì)算方法，對0.4～1.6 之間8 種馬赫數(shù)下大展弦比機(jī)翼進(jìn)行了靜氣動(dòng)彈性數(shù)值研究，結(jié)果表明：機(jī)翼翼尖位移和機(jī)翼最大應(yīng)力在跨音速范圍發(fā)生了突變。可為相關(guān)大展弦比機(jī)翼的設(shè)計(jì)與分析提供參考。劉燚等[23]采用曲面渦格法對柔性飛機(jī)進(jìn)行非線性靜氣動(dòng)彈性分析，結(jié)果表明：曲面渦格法在可壓縮情況下載荷計(jì)算精度較好且氣動(dòng)力曲面建模優(yōu)勢明顯，可用于工程復(fù)雜模型的曲面氣動(dòng)力計(jì)算。

本文針對壁板在跨音速流中的穩(wěn)定性和流固耦合形態(tài)演變規(guī)律展開研究，分析壁板在不同結(jié)構(gòu)和流動(dòng)參數(shù)下隨馬赫數(shù)變化過程中的形態(tài)演化規(guī)律；考慮非定常加速效應(yīng)的影響，分析不同加速比下的形態(tài)演化；考慮粘性效應(yīng)的影響，分析不同邊界層厚度下的形態(tài)演化。

1 基于CFD/CSD 耦合的壁板非線性響應(yīng)分析方法

為了求解由氣動(dòng)和結(jié)構(gòu)兩場非線性引起的非線性壁板非線性響應(yīng)問題，采用了CFD/CSD 時(shí)域耦合求解方法[24-25]，其基本流程(圖1)如下：

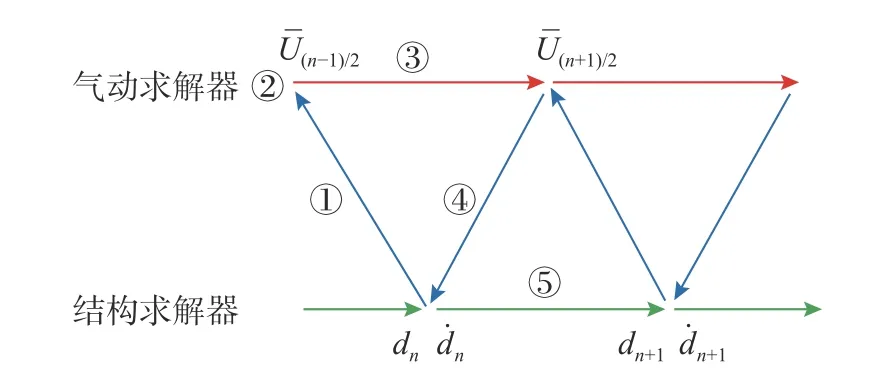
圖1 CFD/CSD 耦合流程Fig. 1 Sketch of CFD/CSD coupling method

式中：S為流場和結(jié)構(gòu)系統(tǒng)之間的轉(zhuǎn)換矩陣[26]；x(n+1/2)為在第 (n+1/2)時(shí)刻流體域中表面網(wǎng)格節(jié)點(diǎn)的位移。

2) 利用動(dòng)網(wǎng)格技術(shù)更新流體網(wǎng)格。考慮慣性力影響，在流固耦合邊界上設(shè)置壓力梯度條件：

2 壁板模型與算法驗(yàn)證

2.1 壁板模型

二維壁板幾何模型和計(jì)算域如圖2 所示，壁板長度為a、厚度為h。彈性薄壁板邊緣固定并與剛性表面平滑連接，薄壁板的邊界條件為固支。當(dāng)在無粘條件下計(jì)算時(shí)，剛性表面設(shè)置為無穿透條件，L1=L2=L3=10a。當(dāng)考慮粘性條件時(shí)，剛性表面設(shè)置為無滑移條件，并且使L1具有恰當(dāng)?shù)拈L度，使求解薄壁板處的流場時(shí)，可以形成具有所需厚度的粘性邊界層，如圖3 所示。

圖2 壁板的幾何模型和計(jì)算域Fig. 2 Panel model and computational domain

圖3 壁板粘性邊界層的形成Fig. 3 Viscous boundary layer of the panel

來流馬赫數(shù)和密度定義為M∞和 ρ∞。壁板基準(zhǔn)模型參數(shù)設(shè)置為[17]：a=0.3m，a/h=300，E=2×1011Pa ，泊松比ν=0.3 ，壁板密度ρs=7800 kg/m3。為方便對比分析，定義如下參數(shù)：

2.2 壁板氣動(dòng)彈性響應(yīng)驗(yàn)證

2.2.1 網(wǎng)格無關(guān)性和時(shí)間步長收斂性分析

研究了不同網(wǎng)格尺寸和時(shí)間步長下M∞=1.12，μ=1.64×10-4時(shí)的壁板響應(yīng)。壁板結(jié)構(gòu)的有限元模型由20 個(gè)單元組成，考慮了壁板的兩端固支邊界條件。計(jì)算工況如表1 所示。

表1 網(wǎng)格數(shù)量和時(shí)間步長的計(jì)算工況Table 1 Calculation conditions of grid size and time-step

圖4 顯示了在不同網(wǎng)格數(shù)量下的計(jì)算結(jié)果在壁板參考點(diǎn)(x/a=0.75)處的時(shí)間歷程曲線，可以看到，在不同網(wǎng)格數(shù)量下，壁板極限環(huán)振幅完全相同的，隨著時(shí)間推移，瞬時(shí)相位有微小的差異。圖5 顯示了在不同時(shí)間步長下的計(jì)算結(jié)果，發(fā)現(xiàn)在不同時(shí)間步長下，極限環(huán)幅值完全相同，但隨著時(shí)間推移，極限環(huán)也有微小相移。綜合考慮計(jì)算精度和效率，本文最后選用的網(wǎng)格數(shù)量為161×101，時(shí)間步長為0.00001 s。

圖4 不同網(wǎng)格數(shù)量下的壁板響應(yīng)Fig. 4 Response of panel under different number of grids

圖5 不同時(shí)間步長下獲得的壁板響應(yīng)Fig. 5 Response of panel under different time-steps

2.2.2 二維壁板跨音速穩(wěn)定性分析驗(yàn)證

為驗(yàn)證本文算法的可靠性，壁板參數(shù)與文獻(xiàn)[6,8,10,13]相同：a/h=50，E=7×1010Pa，泊松比ν=0.3 ，質(zhì)量比μs=0.1。

計(jì)算了馬赫數(shù)從0.8～1.3 時(shí)壁板的穩(wěn)定邊界，并引用了文獻(xiàn)[6,8,13]的結(jié)果，繪制在圖6 中進(jìn)行比較。如圖所示，當(dāng)M∞≤1時(shí)，壁板的不穩(wěn)定形式表現(xiàn)為屈曲，當(dāng)M∞＞1時(shí)，壁板不穩(wěn)定表現(xiàn)為顫振及極限環(huán)振蕩等形態(tài)。這種不穩(wěn)定的邊界結(jié)合到一起，也會表現(xiàn)出一般升力面構(gòu)型(如翼、舵結(jié)構(gòu)等)在跨音速流中的顫振凹坑現(xiàn)象。圖6 顯示了土星五號的飛行軌跡，可以看出，在M∞≈1的區(qū)域內(nèi)，不穩(wěn)定的臨界動(dòng)壓明顯低于飛行動(dòng)壓。DOWELL[6]、DAVIS 等[8]及ALDER[13]的研究都表明了這一點(diǎn)，從計(jì)算結(jié)果來看，本文與DAVIS 和ALDER 等的結(jié)果相符較好，由于DOWELL 的計(jì)算中采用了勢流理論(在M∞=1時(shí)有奇異)，有較大差異。圖7顯示了M∞=0.9時(shí)不同動(dòng)壓下參考點(diǎn)的屈曲位置，可以看出，在不同的擾動(dòng)下，壁板屈曲的平衡位置有兩個(gè)。當(dāng)動(dòng)壓較小時(shí)，這兩個(gè)屈曲位置相對于壁板初始位置是對稱的，隨著動(dòng)壓增大，屈曲位置呈現(xiàn)出不對稱，這種不對稱與較大動(dòng)壓下不同擾動(dòng)所造成的激波強(qiáng)弱有關(guān)，從該算例在跨音速范圍內(nèi)的計(jì)算來看，本文所使用的方法與文獻(xiàn)[10]對比符合較好。

圖6 壁板在跨音速范圍內(nèi)的穩(wěn)定邊界Fig. 6 Stable boundary of panel in transonic domain

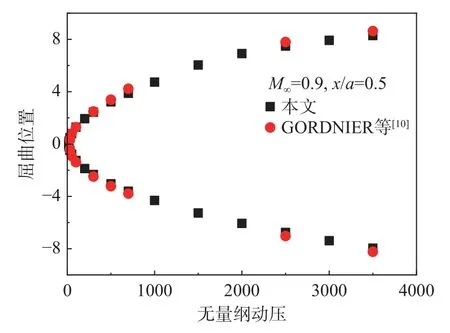
圖7 壁板參考點(diǎn)位置隨動(dòng)壓的變化Fig. 7 Deflection of the panel vs. dynamic pressure

3 跨音速流中定常狀態(tài)下壁板流固耦合形態(tài)演化分析

3.1 計(jì)算條件

考慮了無粘條件下的3 種壁板模型，三種計(jì)算工況如表2 所示。基準(zhǔn)狀態(tài)壁板模型參數(shù)設(shè)置如第2.1 節(jié)所示，而針對壁板長厚比和來流密度(來流動(dòng)壓)變化的壁板模型見表2。初始擾動(dòng)為(考慮了結(jié)構(gòu)前2 階模態(tài)形式)：v=0.001sin(πx/a)+0.001sin(2πx/a) 。 馬赫數(shù)范圍為 0.7≤M∞≤2.0。利用CFD/CSD 耦合方法計(jì)算壁板響應(yīng)，通過壁板參考點(diǎn)(x/a=0.75)的響應(yīng)歷程、頻譜圖、龐加萊映射圖、相平面圖等分析和判別壁板形態(tài)。

表2 三種工況的參數(shù)Table 2 Calculation conditions of three panel models

3.2 定常情況下壁板的形態(tài)演化

壁板的形態(tài)隨著馬赫數(shù)增大的變化過程如圖9 所示。圖10 和圖11 分別顯示了參考點(diǎn)變形位置/振蕩幅值、振蕩頻譜峰主導(dǎo)頻率隨馬赫數(shù)的變化，可以發(fā)現(xiàn)：

圖9 隨馬赫數(shù)變化下三種壁板的形態(tài)演化Fig. 9 Morphological evolution of three kinds of panels with Mach number

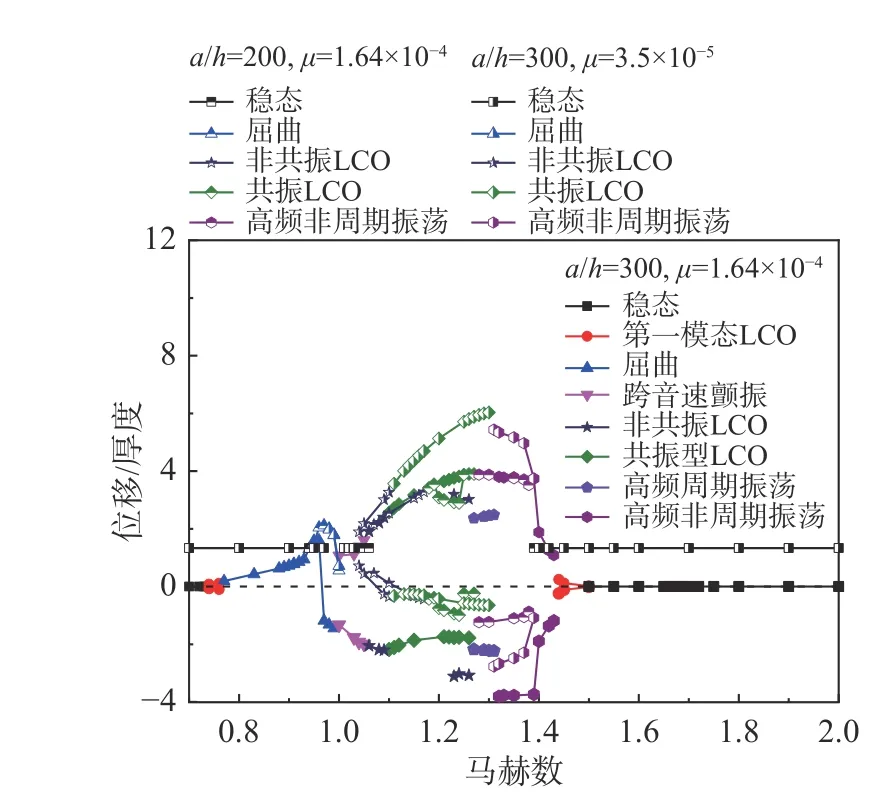
圖10 變形/幅值隨馬赫數(shù)的變化Fig. 10 Deflection/ Amplitude of the panel vs. Mach number

圖11 振蕩主頻隨馬赫數(shù)變化Fig. 11 Main frequency of oscillation vs. Mach number

1) 對于三種壁板計(jì)算工況，隨馬赫數(shù)的逐漸增大，壁板的響應(yīng)形態(tài)大體上從穩(wěn)態(tài)收斂、第一模態(tài)極限環(huán)(LCO)振蕩、屈曲、跨音速顫振、非共振型極限環(huán)(LCO)、共振型極限環(huán) (LCO)、高頻周期振蕩、高頻非周期振蕩到穩(wěn)態(tài)收斂的過程，這與文獻(xiàn)[17]的結(jié)果大體一致。

2) 第一模態(tài)極限環(huán)振蕩、跨音速顫振和非共振型極限環(huán)振蕩、共振型LCO 的形態(tài)如圖12～圖14 所示，可以觀察到，第一模態(tài)極限環(huán)表面為純單模態(tài)振蕩形式，其振蕩頻率為13 Hz，遠(yuǎn)遠(yuǎn)小于一階固有頻率ω0=61.76 Hz。跨音速顫振會表現(xiàn)出明顯的非對稱延遲現(xiàn)象，這是由流場中存在的多激波結(jié)構(gòu)，以及激波前后移動(dòng)所導(dǎo)致(如圖15所示)，此時(shí)頻譜由多個(gè)峰值組成，主頻在壁板固有頻率附近，這種現(xiàn)象在GORDNIER 等[10]和ALDER[13]的研究中也有所體現(xiàn)。當(dāng)壁板厚度增加(Case 2)、或者來流密度變小(Case 3)，并未觀察到明顯帶有延遲振蕩的跨音速顫振。隨馬赫數(shù)增加，延遲振蕩變?nèi)酰尸F(xiàn)為如圖14 所示對稱形式，振蕩頻譜的3 個(gè)峰值近似為1∶2∶3 組成，其中第二模態(tài)是一個(gè)小的分量，隨著馬赫數(shù)的增加，該分量比例逐漸增加，向共振型LCO 過渡。其演化機(jī)理大體如下：隨著馬赫數(shù)的增大，氣流的能量也增大，氣流能量向結(jié)構(gòu)傳遞的過程中，可能會引起其第一模態(tài)的增長，第一模態(tài)增長過程中，振蕩頻率也會增加，存在一個(gè)臨界值，之后會激發(fā)第二模態(tài)，其增長通過與第一模態(tài)的共振來維持，隨著氣流能量的繼續(xù)增加，第二模態(tài)的主導(dǎo)作用也越來越明顯，當(dāng)流入壁板的能量等于流出壁板的能量時(shí)，第一、二階模態(tài)的振幅達(dá)到穩(wěn)定，進(jìn)入極限環(huán)振蕩。相似的分析可見文獻(xiàn)[27]。

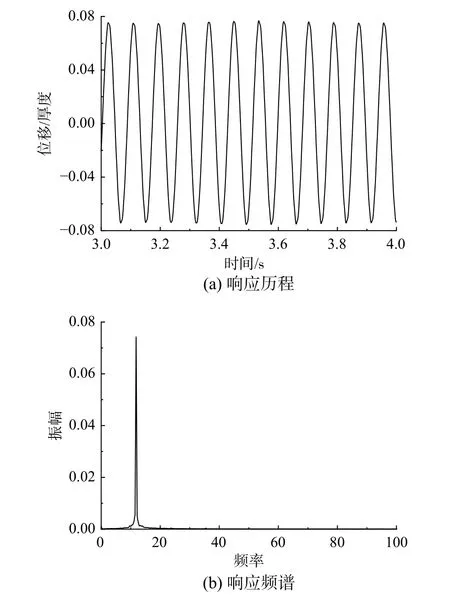
圖12 工況1 第一模態(tài)LCO 的響應(yīng)和頻譜圖Fig. 12 Time-histories and frequency spectrum of first-mode LCO (Case 1)

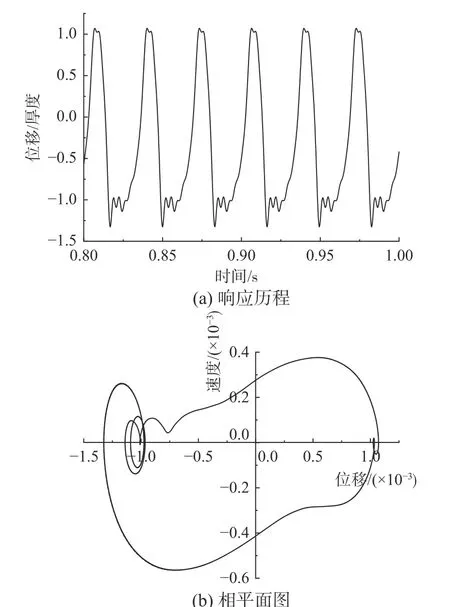
圖13 工況1 跨音速顫振的響應(yīng)和相圖Fig. 13 Time-histories and phase portraits of transonic flutter (Case 1)

圖14 工況1 非共振型LCOFig. 14 Time-histories and phase portraits of nonresonant LCO (Case 1)

圖15 工況1 跨音速顫振瞬時(shí)φ=180°的流場壓強(qiáng)Fig. 15 Pressure distributions at φ=180° of transonic flutter (Case 1)

3) 亞音速下的第一模態(tài)LCO 和跨音速顫振中，其振蕩主頻低于壁板第一階固有頻率值，表現(xiàn)為單模顫振，與經(jīng)典顫振中兩個(gè)或者多個(gè)結(jié)構(gòu)模態(tài)耦合形成機(jī)理不一樣的是，其形成是由于氣流的不穩(wěn)定引起的，因此產(chǎn)生的顫振模態(tài)可能同時(shí)來源于壁板的結(jié)構(gòu)模態(tài)和氣流模態(tài)。當(dāng)壁板發(fā)生共振極限環(huán)發(fā)生時(shí)，表現(xiàn)為耦合模態(tài)振蕩，如圖16 所示，此時(shí)隨馬赫數(shù)的增加，主頻增長減慢(圖11)。

圖16 工況1 共振型LCO 的響應(yīng)和頻譜圖Fig. 16 Time-histories and frequency spectrum of resonant LCO (Case 1)

4) 對于高頻周期和非周期振蕩而言，振蕩中存在多個(gè)高頻模態(tài)，此區(qū)域很可能是疲勞損傷最嚴(yán)重的區(qū)域：即使偏轉(zhuǎn)幅值與第一模態(tài)極限環(huán)相近，但其壁板形態(tài)包含較高的模態(tài)，因此應(yīng)力振幅比第一模態(tài)極限環(huán)的應(yīng)力振幅高得多，此外，該區(qū)域包含較高的頻率，因此一旦產(chǎn)生，極有可能會在短時(shí)間內(nèi)迅速積累大量的疲勞損傷。

5) 在更大的壁板厚度(工況2)和更小的動(dòng)壓(工況3)下，壁板演化過程與基準(zhǔn)狀態(tài)(工況1)相比主要有3 點(diǎn)不同：

a) 在亞音速區(qū)沒有第一模態(tài)極限環(huán)振蕩；

b) 由于壁板較厚(或由于無量綱氣流密度較小，即動(dòng)壓較小)，M∞=1時(shí)無法激發(fā)出跨音速顫振，反而保持穩(wěn)定狀態(tài)；

c) 在低超音速區(qū)，作為過渡的高頻周期振蕩和第一模態(tài)極限環(huán)振蕩沒有激發(fā)，表現(xiàn)為高頻非周期振蕩。

3.3 考慮非定常加速效應(yīng)下壁板的形態(tài)演化分析

3.3.1 計(jì)算條件

針對三個(gè)計(jì)算工況，定義非定常加速中馬赫數(shù)的變化如下[18]：

其中，M1=0.7 和M2=1.7。通過調(diào)整時(shí)間T來改變流動(dòng)的加速度。為了使得壁板響應(yīng)進(jìn)入M1和M2之間前得到較為穩(wěn)定的形態(tài)，選取適當(dāng)?shù)腗0即可。分析中取T=10 s、5 s 和2.5 s，代表了加速度從小到大。需要注意的是，該加速條件是通過遠(yuǎn)場邊界實(shí)施，加速效應(yīng)對壁板產(chǎn)生的影響會存在一定的時(shí)間延遲，但總體延遲時(shí)間很小，分析的幾種工況不大于0.004 s。

3.3.2 加速條件下壁板的形態(tài)演化

當(dāng)考慮非定常加速效應(yīng)時(shí)，壁板的形態(tài)演化如圖17 所示；參考點(diǎn)偏轉(zhuǎn)的時(shí)間歷程如圖18 所示；龐加萊映射如圖19 所示，從圖中可以清楚地看到壁板塊動(dòng)力學(xué)的大部分分岔。不同加速情況下振幅和主導(dǎo)頻率與馬赫數(shù)的關(guān)系比較如圖20 所示(灰色點(diǎn)線圖為定常馬赫數(shù)下壁板響應(yīng)的幅值和頻率)，可以看出：

圖17 不同加速度下壁板的形態(tài)演化(工況1)Fig. 17 Morphological evolution of panels under different accelerations (Case 1)

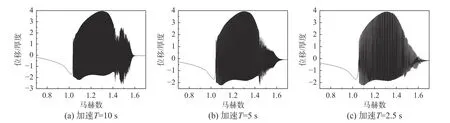
圖18 不同加速情況下的壁板響應(yīng)歷程Fig. 18 Response history of panel under different acceleration

圖19 不同加速情況下的龐加萊映射Fig. 19 Poincare maps under different accelerations

1) 在亞音速情況下，所有加速度下的響應(yīng)幅值都接近于定常流中的幅值，加速度越大，屈曲區(qū)的值越大，且馬赫數(shù)越接近1，不同加速度下幅值差異越小(圖20(a))。

圖20 不同加速度條件下的振幅和主導(dǎo)頻率Fig. 20 Amplitude and dominant frequency under different accelerations

2) 在跨音速時(shí)，具有非定常加速效應(yīng)時(shí)發(fā)生振蕩所需的馬赫數(shù)略大，且加速度越大，振蕩發(fā)生的馬赫數(shù)越大，即振蕩延遲越明顯。

3) 在 1≤M∞≤1.26時(shí)，具有非定常加速效應(yīng)和定常時(shí)的結(jié)果吻合的很好，不僅振幅接近，而且主導(dǎo)頻率只有第一和第二頻率。

4) 對于更高的馬赫數(shù)，存在明顯差異：

a) 不存在作為過渡的高頻周期振蕩；

b) 由于更高頻率的振蕩需要較多的時(shí)間去發(fā)展，當(dāng)加速度較低時(shí)(T=10 s、T=5 s)，高頻振蕩發(fā)生的馬赫數(shù)大于定常流發(fā)生高頻振蕩所對應(yīng)的馬赫數(shù)，振蕩幅值小于定常流，且隨著加速度的提高，高頻振蕩發(fā)生的馬赫數(shù)逐漸提高，振蕩幅值減小，但高頻區(qū)頻譜中高頻占比要大于定常流流，且頻率值隨馬赫數(shù)增加有一個(gè)明顯的先快速提高后快速下降的過程(圖20(b))；

c) 對于較高的加速度(T=2.5 s)，較高頻率發(fā)展所需的時(shí)間顯得有些過長，在高頻分量明顯顯現(xiàn)之前，流速已經(jīng)跨越可以支撐高頻分量繼續(xù)發(fā)展的馬赫數(shù)域，因此高頻振蕩將不會產(chǎn)生；

d) 當(dāng)T=5 s 時(shí)，存在一個(gè)過渡狀態(tài)—高頻準(zhǔn)周期運(yùn)動(dòng)，其頻率主導(dǎo)模態(tài)為六階模態(tài)；

e) 當(dāng)T=2.5 s 時(shí)，共振極限環(huán)會演化為一個(gè)第一、二階模態(tài)交替的新形態(tài)，演化較為平滑，無法準(zhǔn)確確定分岔點(diǎn)，在該階段壁板形狀有兩個(gè)形態(tài)，分別接近第一階振型和第二階振型，兩種形態(tài)交替出現(xiàn)交替主導(dǎo)。當(dāng)M∞≈1.7 時(shí)，振蕩幅值極小，接近消失。

圖21 和圖22 顯示了壁板厚度增加(工況2)和來流密度減小后(工況3)的非定常計(jì)算結(jié)果，可以看出：

圖21 不同加速度下壁板的形態(tài)演化(工況2)Fig. 21 Morphological evolution of panels under different accelerations (Case 2)

圖22 不同加速度下壁板的形態(tài)演化(工況3)Fig. 22 Morphological evolution of panels under different accelerations (Case 3)

1) 在亞音速、跨音速和馬赫數(shù)較低的低超音速域，可以得到與基準(zhǔn)狀態(tài)相同的結(jié)論。

2) 在馬赫數(shù)較大時(shí)，對于工況2，在加速情況下，當(dāng)M∞≥1.38時(shí)壁板幅值將緩慢減小，直到馬赫數(shù)接近1.7 才會恢復(fù)為屈曲狀態(tài)。當(dāng)加速度較小(T=10 s)時(shí)，在這一區(qū)域?qū)⒋嬖谝粋€(gè)頻率略小于定常流、幅值初始值接近最大幅值且隨馬赫數(shù)增加而逐漸減小的高頻非周期運(yùn)動(dòng)；當(dāng)加速度較大(T=2.5 s)時(shí)，高頻區(qū)被跨過，相應(yīng)的馬赫數(shù)域由一個(gè)幅值隨馬赫數(shù)增加而逐漸減小的第一模態(tài)極限環(huán)振蕩所代替。

3) 在馬赫數(shù)較大時(shí)，對于工況3，當(dāng)加速度較小(T=10 s)時(shí)，存在一個(gè)馬赫數(shù)域較廣(類似于壁板更厚的情況)但幅值較低(類似于基準(zhǔn)狀態(tài))、頻率較低的高頻非周期振蕩；當(dāng)加速度較大(T=2.5 s)時(shí)，高頻區(qū)被跨過。

3.4 考慮粘性效應(yīng)下壁板形態(tài)的演化分析

3.4.1 計(jì)算條件

為了分析粘性效應(yīng)對流固耦合形態(tài)演化規(guī)律的影響，取壁板中心點(diǎn)距上方99%遠(yuǎn)場速度處位置為附面層的外邊界。本文針對兩種不同附面層厚度 δ/a=0.025 和 δ/a=0.05進(jìn)行分析，為取得對應(yīng)的附面層厚度，通過調(diào)整壁板前端到遠(yuǎn)場的距離L1，來發(fā)展形成附面層，如圖3 所示。

3.4.2 定常條件下壁板的形態(tài)演化

定常條件不同附面層厚度下壁板的形態(tài)演化如圖23 所示，振幅和主導(dǎo)頻率與馬赫數(shù)的關(guān)系比較如圖24 所示(灰色點(diǎn)線圖為不考慮粘性時(shí)壁板的幅值和頻率)，發(fā)現(xiàn)當(dāng)考慮粘性后：

圖23 不同附面層厚度下壁板的形態(tài)演化Fig. 23 Morphological evolution of panels under different boundary layer thickness

圖24 不同附面層厚度下的振幅和主導(dǎo)頻率Fig. 24 Amplitude and dominant frequency under different boundary layer thickness

1) 亞音速下的穩(wěn)態(tài)和第一模態(tài)LCO 轉(zhuǎn)變?yōu)榍缫羲俜秶鷥?nèi)部分馬赫數(shù)下的動(dòng)壓不足以支撐振蕩的產(chǎn)生，壁板的振蕩恢復(fù)為屈曲狀態(tài)。

2) 較高的模態(tài)會產(chǎn)生較大的阻尼，使得在無粘模型高頻區(qū)用來使較高模態(tài)發(fā)展增長的這一部分能量被耗散掉，高頻區(qū)范圍大大縮小，當(dāng)附面層為 δ/a=0.025時(shí)，高頻區(qū)完全消失，壁板形態(tài)由共振極限環(huán)轉(zhuǎn)換為低頻準(zhǔn)周期振蕩(主導(dǎo)模態(tài)仍為第一和第二模態(tài)，但存在多個(gè)峰值)和第一模態(tài)極限環(huán)(壁板運(yùn)動(dòng)接近一階振型)；隨著附面層的繼續(xù)增厚 δ/a=0.05時(shí)，高階模態(tài)的影響將完全消失。

3) 隨著附面層的增厚，壁板振蕩的最大幅值和頻率都會有所減小，而在較高馬赫數(shù)時(shí)(M∞≥1.5)，幅值和頻率反而有所增大。

3.4.3 加速條件下壁板的形態(tài)演化

考慮非定常加速效應(yīng)后(T=10 s、T=2.5 s)不同附面層厚度下壁板的形態(tài)演化如圖25 和圖26所示，振幅和主導(dǎo)頻率與馬赫數(shù)的關(guān)系比較如圖27和圖28 所示，結(jié)果表明：

圖25 不同加速度下壁板的形態(tài)演化(δ/a=0.025)Fig. 25 Morphological evolution of panels under different accelerations (δ/a=0.025)

圖26 不同加速度下壁板的形態(tài)演化(δ/a=0.05)Fig. 26 Morphological evolution of panels under different accelerations (δ/a=0.05)

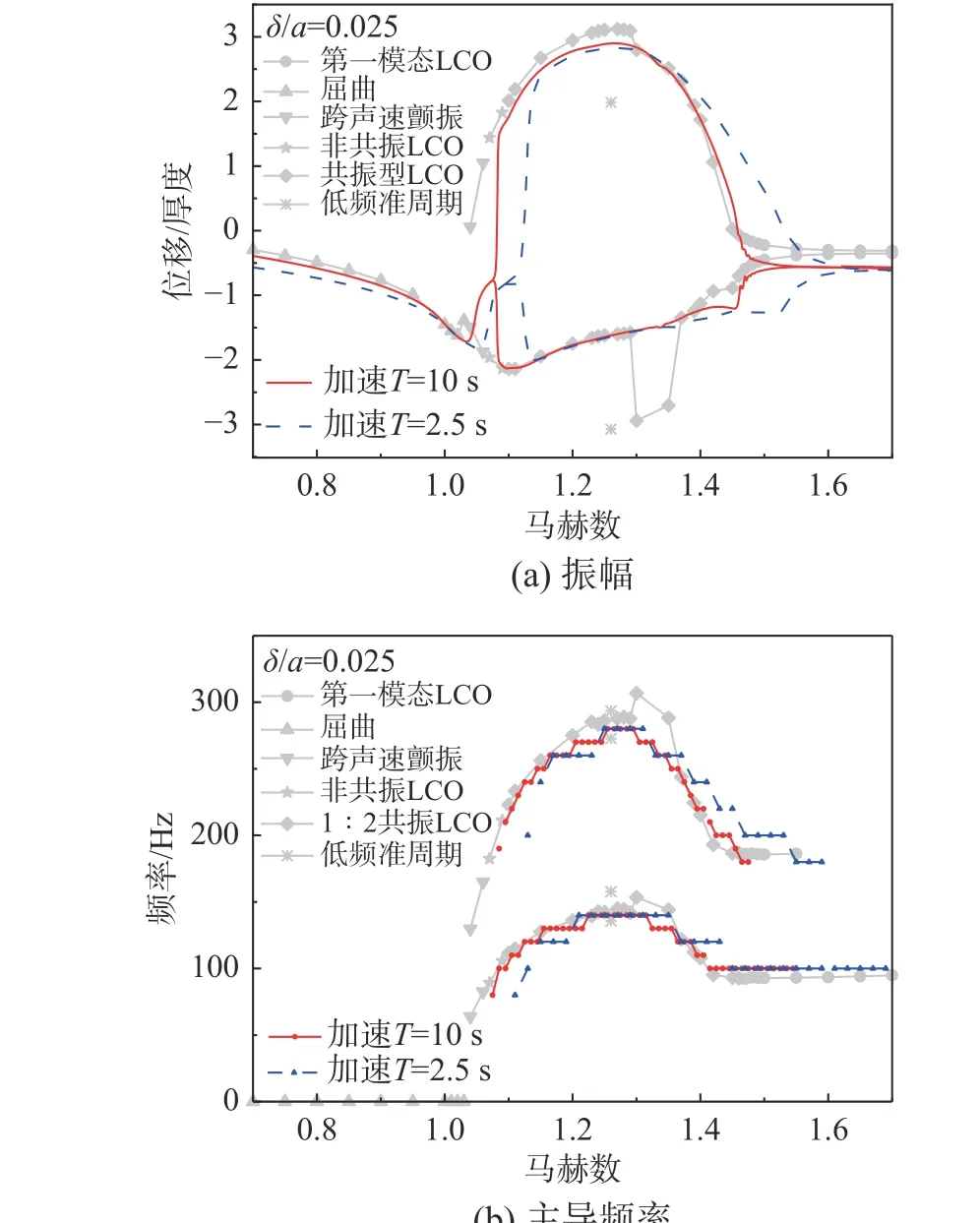
圖27 δ/a=0.025時(shí)不同加減速條件下的振幅和主導(dǎo)頻率Fig. 27 Amplitude and dominant frequency under different accelerations ( δ/a=0.025)

1) 考慮非定常加速效應(yīng)后，振蕩起始和結(jié)束的馬赫數(shù)會向較大的馬赫數(shù)偏移，附面層越厚偏移越明顯。

2) 隨著加速度的提高，最大幅值和最大頻率均有所減小，附面層越厚越明顯。

3) 當(dāng) δ/a=0.025時(shí)，在原高頻域，當(dāng)具有加速效應(yīng)后，由于附面層厚度不足導(dǎo)致的演化不再出現(xiàn)。

4) 考慮非定常效應(yīng)后振蕩的主頻隨馬赫數(shù)呈現(xiàn)出臺階式變化，即在一定馬赫數(shù)范圍內(nèi)，振蕩主頻保持不變，加速度越高、附面層越厚，這種臺階狀變化越明顯(圖27(b)、圖28(b))，這與考慮粘性效應(yīng)后阻尼增大有關(guān)。

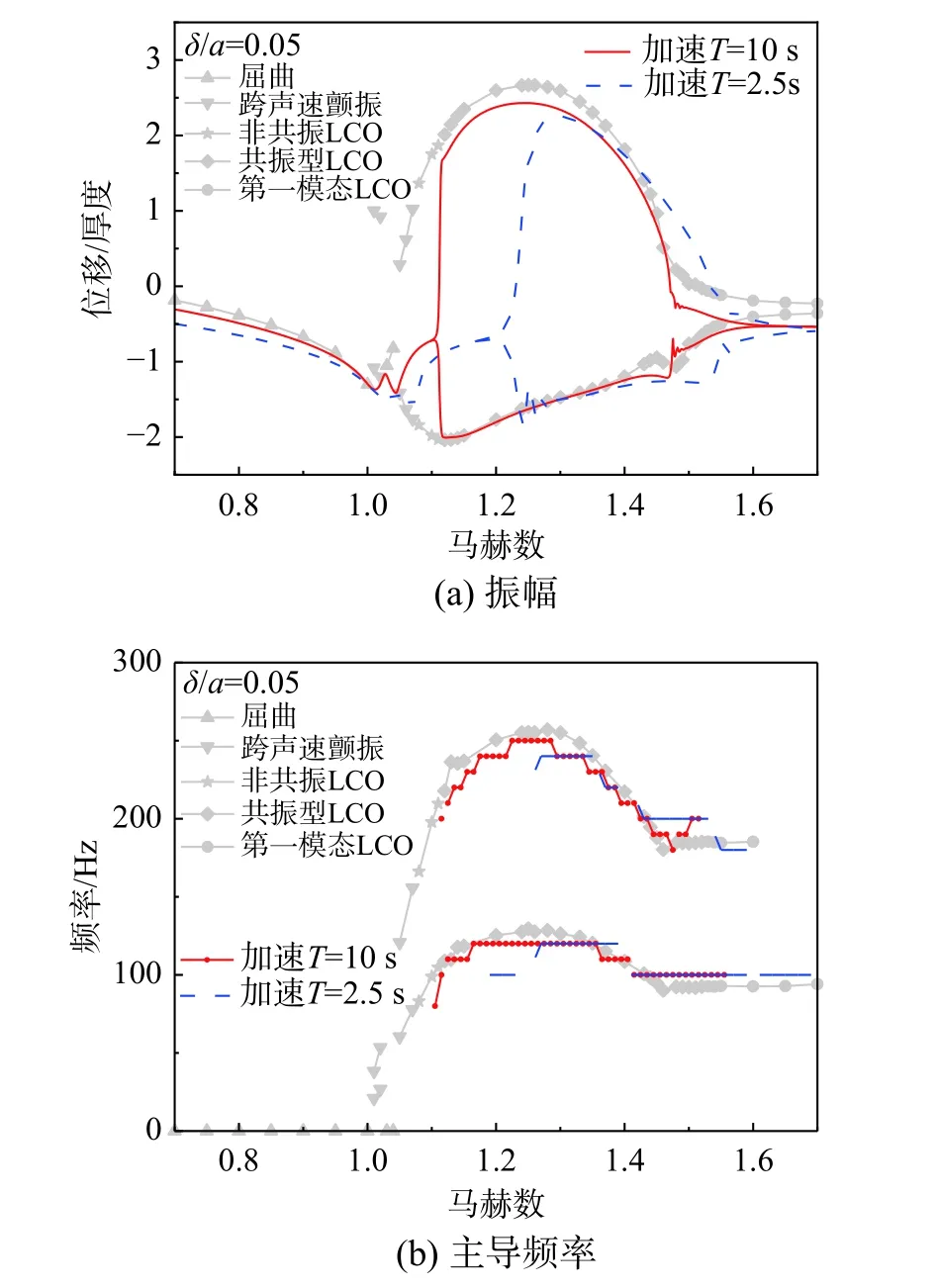
圖28 δ/a=0.05時(shí)不同加速條件下的振幅和主導(dǎo)頻率Fig. 28 Amplitude and dominant frequency under different accelerations ( δ/a=0.05)

4 結(jié)論

本文基于CFD/CSD 耦合方法，分析了跨音速范圍內(nèi)壁板形態(tài)的演化規(guī)律。從仿真結(jié)果分析總結(jié)出如下規(guī)律：

(1) 在跨音速范圍內(nèi)，隨著馬赫數(shù)的增加，壁板的響應(yīng)呈現(xiàn)出復(fù)雜的演化形態(tài)：穩(wěn)態(tài)收斂、第一模態(tài)LCO、屈曲、跨音速顫振、非共振型LCO、共振型LCO、高頻周期振蕩、高頻非周期振蕩等，其中亞音速下的第一模態(tài)LCO、跨音速顫振和非共振型LCO 的振蕩主頻小于結(jié)構(gòu)1 階固有頻率，呈現(xiàn)出單模態(tài)顫振的形態(tài)。

(2) 從壁板隨馬赫數(shù)的變化來看，非周期振蕩區(qū)域出現(xiàn)了高振幅和高頻率特征，很可能是典型的單模顫振中疲勞損傷最嚴(yán)重的區(qū)域。

(3) 考慮非定常加速效應(yīng)后，各演化階段向馬赫數(shù)更大的方向推移。當(dāng)來流加速度增加時(shí)，發(fā)生高頻振蕩的馬赫數(shù)范圍會變短，如果加速度足夠大，則高頻振蕩形態(tài)會消失。

(4) 當(dāng)考慮粘性效應(yīng)后，高頻區(qū)范圍將大大縮小，并隨著附面層的增厚，高頻區(qū)最終完全消失。且振蕩的主頻呈現(xiàn)出臺階式變化，加速度越高、附面層越厚，這種臺階狀變化越明顯。

(5) 總體來看，當(dāng)考慮非定常加速效應(yīng)和粘性效應(yīng)后，對于單模態(tài)顫振發(fā)生會延遲，對于引起壁板疲勞損傷最為嚴(yán)重的高頻振蕩會有所抑制，這在飛行器設(shè)計(jì)中是有利的因素，傳統(tǒng)基于無粘假設(shè)和定常分析的結(jié)果偏于保守。