基于窮舉搜索策略與邏輯回歸算法的RC 柱地震破壞模式判別模型

喻澤成，李啟明，謝龍隆，余 波,2,3

(1. 廣西大學土木建筑工程學院，廣西，南寧 530004；2. 工程防災與結構安全教育部重點實驗室，廣西，南寧530004；3. 廣西防災減災與工程安全重點實驗室，廣西，南寧 530004)

歷次地震災害顯示，橋梁、建筑等工程結構的鋼筋混凝土(RC)柱在強震作用下可能發生彎曲破壞、彎剪破壞或剪切破壞，影響工程結構的安全性[1-3]。因此，有必要識別RC 柱地震破壞模式的重要特征參數，并建立地震破壞模式的判別方法。

目前，RC 柱的地震破壞模式判別方法主要有經驗判別法和機器學習判別法兩大類。其中，經驗判別法基于工程經驗或試驗數據分析，建立位移延性系數[4]、剪跨比[5]、抗剪需求與抗剪承載力比[6]等特征參數與地震破壞模式之間的關系。例如，文獻[7]綜合考慮剪跨比、軸壓比、縱筋特征參數和箍筋特征參數的影響，提出了RC 柱地震破壞模式的經驗判別指標；文獻[8]根據抗剪需求與抗剪承載力比、剪跨比、箍筋間距與截面有效高度比來綜合判別RC 柱的地震破壞模式。分析表明：經驗判別法具有簡便實用的優點，但通常是基于工程經驗或試驗數據相關性分析建立的，導致特征參數與地震破壞模式之間缺乏內在聯系，判別準確率不高[9]。機器學習判別法結合試驗數據和各種機器學習算法，構建特征參數與地震破壞模式之間的聯系[10]。其中，文獻[11]采用隨機森林算法判別RC 柱的地震破壞模式；文獻[12]對比分析了6 種機器學習算法對于RC 柱地震破壞模式的判別精度；文獻[13]結合機器學習的回歸算法和分類算法，建立了RC 柱的地震破壞模式判別方法。然而，上述機器學習判別法存在以下缺陷：一是所建立的判別模型雖然可以構建輸入特征參數與輸出破壞模式之間的映射關系，但是沒有建立二者之間的顯式函數表達式，屬于“黑盒”模型[11-14]；二是建模過程中沒有遴選特征參數，通常將全部特征參數作為模型輸入變量，導致所建立的判別模型復雜程度高、計算效率低[15]；三是難以定量分析輸入特征參數對輸出破壞模式的影響程度，導致模型的可解釋性差。因此，有必要合理遴選RC 柱地震破壞模式的最優特征參數，并建立具有明確函數表達式且簡便實用的地震破壞模式判別模型。

鑒于此，本文首先基于窮舉搜索策略，分別遴選了判別彎曲破壞與非彎曲破壞以及彎剪破壞與剪切破壞的最優特征參數；然后結合最優特征參數和邏輯回歸算法，建立了RC 柱地震破壞模式判別的兩階段邏輯回歸模型(即先判別彎曲破壞和非彎曲破壞，然后判別彎剪破壞和剪切破壞)；最后通過與經典邏輯回歸算法和傳統經驗判別方法進行對比分析，驗證了該模型的有效性。

1 地震破壞模式判別的邏輯回歸算法

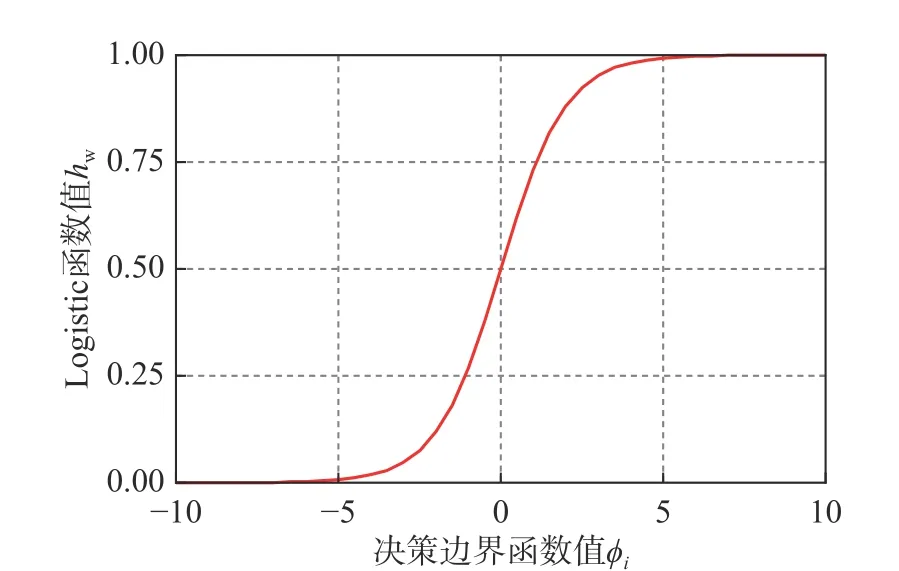
圖1 Logistic 函數曲線Fig. 1 Curve of Logistic function

根據邏輯回歸模型[17]，當第i條RC 柱屬于特定類的概率大于非特定類的概率(即Rp＞0)時，判定類標簽yi=1；當第i條RC 柱屬于特定類的概率小于非特定類的概率(Rp＜0 ) 時，判定類標簽yi=0。

為了求解式(2)中的參數w和b，假定m組地震破壞模式樣本之間相互獨立，根據式(1)可以構造邏輯回歸模型的極大似然估計函數L(w,b)[18]：

2 基于窮舉搜索策略的最優特征參數遴選

影響RC 柱地震破壞模式的特征參數較多，包括抗剪需求與抗剪承載力比(Vp/Vn)、箍筋間距與截面有效高度比(s/h0)、縱筋特征參數、箍筋特征參數、剪跨比和軸壓比等[5-8,20-21]。然而，不同特征參數對RC 柱地震破壞模式的影響程度存在明顯差異。因此，本文首先基于窮舉搜索策略，分別遴選了判別彎曲破壞與非彎曲破壞以及彎剪破壞與剪切破壞的最優特征參數。

2.1 地震破壞模式判別的原始特征參數

國內外學者圍繞RC 柱地震破壞模式的特征參數分析開展了廣泛研究。其中，文獻[7]研究分析了縱筋特征參數(αl=ρlfyl/fc′)、軸壓比(n)、箍筋特征參數(αv=ρvfyv/ft)和剪跨比(a/h0)對RC 柱的地震破壞模式的影響，發現隨著αl和n的增大，或者αv和a/h0的減小，RC 柱的地震破壞模式逐漸從彎曲破壞向彎剪或剪切破壞轉變；文獻[8]研究表明：箍筋間距與截面有效高度比(s/h0)對RC柱的地震破壞模式具有顯著影響，隨著s/h0的增大，RC 柱的地震破壞模式逐漸由彎曲破壞向彎剪破壞和剪切破壞轉變；文獻[20]研究了αl和a/h0對RC 柱地震破壞模式的影響，發現隨著αl增大或a/h0減小，RC 柱的地震破壞模式逐漸由彎曲破壞向剪切破壞轉變；文獻[5]研究發現剪跨比與RC 柱的地震破壞模式具有較強相關性，對于高、中和低剪跨比，RC 柱依次發生彎曲破壞、彎剪破壞和剪切破壞；文獻[6]認為抗剪需求與抗剪承載力比(Vp/Vn)與RC 柱的地震破壞模式密切相關，Vp/Vn越大，RC 柱越容易發生剪切破壞；文獻[21]分析發現，RC 柱的地震破壞模式與Vp/Vn和a/h0密切相關，Vp/Vn越大，RC 柱越容易發生剪切破壞，而當Vp/Vn較小且a/h0較大時，RC 柱容易發生彎曲破壞和彎剪破壞；這里，ρl和ρv分別為配筋率和配箍率，fyl和fyv分別為縱筋和箍筋的屈服強度，fc′和ft分別為混凝土圓柱體抗壓強度和混凝土抗拉強度，a為剪跨，h0為截面有效高度，s為箍筋間距，Vp為抗剪需求，Vn為抗剪承載力。綜上所述，Vp/Vn、s/h0、αl、αv、a/h0和n對RC 柱的地震破壞模式具有重要影響。因此，本文將上述6 個特征參數選取為RC 柱地震破壞模式的原始特征參數。由于上述特征參數均為無量綱量，所以可以排除量綱的影響。

為了分析上述6 個特征參數對RC 柱地震破壞模式的影響規律，本文從國內外文獻[7, 21 - 42]中收集了270 組矩形截面RC 柱的破壞試驗數據，基本信息見表1。綜合考慮參考文獻中報道的破壞模式、RC 柱的裂縫分布形態、滯回曲線以及破壞過程中箍筋和縱筋的屈服狀態等因素確定了上述270 組RC 柱的破壞模式。繪制不同地震破壞模式下各特征參數的半小提琴圖，如圖2 所示。圖2 中，半小提琴左側為頻率分布圖，右側為小提琴圖，小提琴外部形狀為核密度估計圖，中間白點表示均值，黑線表示標準差范圍。由圖2 可知，當RC 柱的地震破壞模式由彎曲破壞向彎剪破壞轉變、由彎剪破壞向剪切破壞轉變時，Vp/Vn的均值增加率分別為85.5%和32.4%，s/h0的均值增加率分別為40.7%和44.7%，αl的均值增加率分別為20.8%和24.1%，αv的均值減小率分別為43.7%和25.9%，a/h0的均值減小率分別為30.7%和30.3%，n的均值減小率和增大率分別為2.8%和4.5%。由此可見，隨著特征參數Vp/Vn、s/h0和αl的增大，以及αv和a/h0的減小，RC 柱的地震破壞模式逐漸由彎曲破壞逐漸向彎剪破壞和剪切破壞轉變，但是不同特征參數的變化趨勢不同，說明不同特征參數對地震破壞模式的影響程度存在差異。因此，有必要從地震破壞模式的原始特征參數中遴選出RC 柱地震破壞模式的最優特征參數。

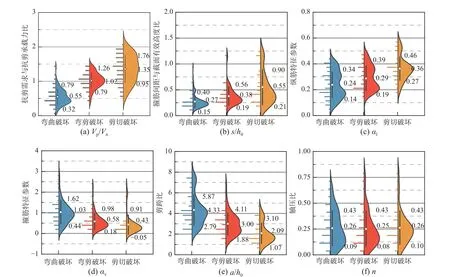
圖2 對應不同地震破壞模式時各特征參數的半小提琴圖Fig. 2 Half violin plot of characteristic parameters for different failure modes

表1 270 組RC 柱試驗數據的基本信息Table 1 Basic information of experimental data of 270 RC columns

2.2 RC 柱地震破壞模式的最優特征參數

式中，子集評價函數f(ak)為地震破壞模式判別模型的性能評價指標(如總體判別準確率)。通過式(6)，可以從k個候選特征參數子集中，遴選出地震破壞模式判別模型的性能評價指標最優時對應的特征參數子集，進而可以遴選出RC 柱地震破壞模式的最優特征參數。需要說明的是，式(6)的最優化問題涉及到兩階段求解：第一階段是計算子集評價函數f(ak)的取值，其關鍵是確定式(5)中的最優參數w? 和b?，采用的算法為梯度下降法和牛頓法；第二階段是在2n-1 個特征子集對應的子集評價函數f(ak)中選取最大值，采用的是簡單排序算法。值得注意的是，窮舉搜索策略屬于完全搜索策略，能克服其他啟發式搜索策略(如序列前向選擇和序列后向選擇等)陷入局部最優的弊端，適用于最優特征參數遴選問題。

3 最優特征參數遴選與地震破壞模式判別模型

由于在強烈地震作用下RC 柱可能發生彎曲破壞、彎剪破壞和剪切破壞，所以RC 柱的地震破壞模式判別屬于多分類問題。然而，傳統的邏輯回歸模型屬于二分類模型[15]，所以無法直接用于RC柱的地震破壞模式判別。因此，本文提出了RC 柱地震破壞模式判別的兩階段邏輯回歸模型：第一階段邏輯回歸模型判別RC 柱是否發生彎曲破壞或非彎曲破壞(包括彎剪破壞和剪切破壞)；第二階段邏輯回歸模型進一步針對非彎曲破壞類別判別RC 柱發生彎剪破壞或剪切破壞。

3.1 兩階段地震破壞模式判別的最優特征參數

為了建立具有明確函數表達式且簡便實用的RC 柱地震破壞模式判別模型，基于窮舉搜索策略，分別遴選了對應于第一階段邏輯回歸模型(判別彎曲破壞和非彎曲破壞)和第二階段邏輯回歸模型(判別彎剪破壞和剪切破壞)的最優特征參數。

為遴選第一階段邏輯回歸模型(判別彎曲破壞和非彎曲破壞)的最優特征參數，首先基于窮舉搜索策略，利用由前述6 個特征參數組成的原始特征 參 數 集 {Vp/Vn,a/h0,s/h0,α1,αv,n} 生 成26-1=63個特征參數候選子集；然后將邏輯回歸模型的最高準確率指標作為確定最優特征參數子集的性能評價指標；最后基于第一階段270 組試驗數據(彎曲破壞135 組和非彎曲破壞135 組)，結合十折交叉驗證方法，確定第一階段邏輯回歸模型的最優特征參數子集，計算結果如圖3(a)所示。由圖3(a)可知，當候選特征參數子集編號k=15 時(對應的特征參數子集為 {Vp/Vn,n})，邏輯回歸模型達到最高判別準確率峰值點；隨著k繼續增加(與候選特征參數子集中特征參數數量增加保持一致)，模型判別準確率并不會明顯提高，甚至反而有所降低。由此可見，第一階段邏輯回歸模型(判別彎曲破壞和非彎曲破壞)的最優特征參數子集為{Vp/Vn,n}。

為遴選第二階段邏輯回歸模型(判別彎剪破壞和剪切破壞)的最優特征參數，基于135 組非彎曲破壞的試驗數據(彎剪破壞62 組、剪切破壞73組)，結合窮舉搜索策略、邏輯回歸算法和十折交叉驗證方法，可以確定第二階段的最優特征參數子集，計算結果如圖3(b)所示。由圖3(b)可知，當k<48 時，邏輯回歸模型的準確率整體上呈增大趨勢，表明邏輯回歸模型的判別性能受到了更多特征參數的影響；當候選特征參數子集編號k=48時(對應的特征參數子集為 {a/h0,s/h0,α1,αv})，邏輯回歸模型達到最高判別準確率，隨著k的繼續增大，邏輯回歸模型的判別準確率無法得到明顯提高，說明此時邏輯回歸模型已達到最優判別性能。因此，第二階段邏輯回歸模型(判別彎剪破壞和剪切破壞)的最優特征參數子集為{a/h0,s/h0,α1,αv}。

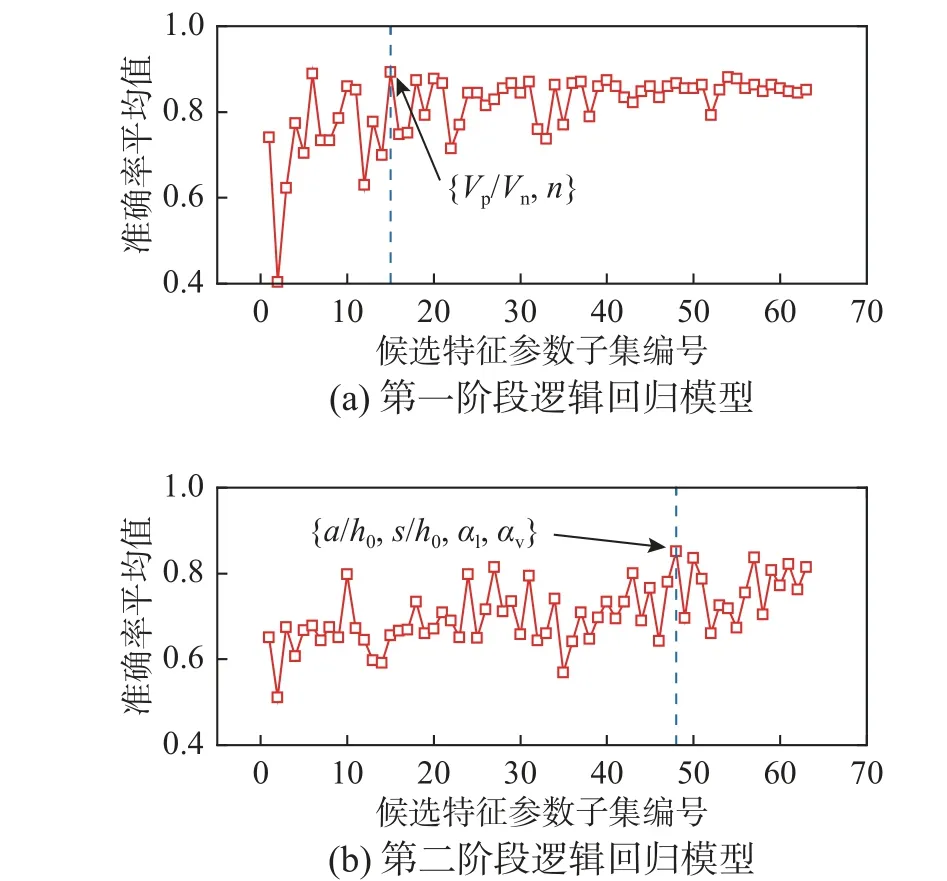
圖3 基于窮舉搜索策略的最優特征參數遴選Fig. 3 Selection of optimal characteristic parameters based on exhaustive search mechanism

綜上所述，判別彎曲破壞與非彎曲破壞的最優特征參數為抗剪需求與抗剪承載力比和軸壓比，而判別彎剪破壞與剪切破壞的最優特征參數為箍筋特征參數、縱筋特征參數、剪跨比、箍筋間距與截面有效高度比。

當建立第一階段邏輯回歸模型(判別彎曲破壞和非彎曲破壞)時，對所收集的270 組(彎曲破壞135 組、彎剪破壞62 組和剪切破壞73 組)RC 柱地震破壞模式試驗數據進行分類，將非彎曲破壞劃分為特定類(共135 組數據)，將彎曲破壞劃分為非特定類(共135 組數據)，然后按照訓練集與測試集的比例為7∶3 將數據集進行分層隨機抽樣，最后以第一階段所遴選的最優特征參數Vp/Vn和n作為輸入變量，利用189 組訓練集樣本數據(包括特定類95 組和非特定類94 組)，訓練第一階段邏輯回歸模型：

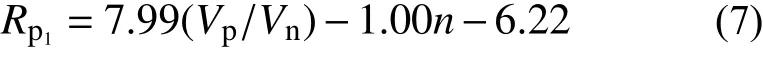
根據式(7)，當Rp1＜0時，表明RC 柱發生非彎曲破壞的概率小于彎曲破壞的概率，則判別RC 柱為彎曲破壞；當Rp1＞0時，表明RC 柱發生非彎曲破壞的概率大于彎曲破壞的概率，則判別RC 柱為非彎曲破壞，進一步可以繼續對該樣本進行彎剪破壞和剪切破壞的判別。

當建立第二階段邏輯回歸模型(判別彎剪破壞和剪切破壞)時，將剪切破壞劃分為特定類(共73 組數據)，將彎剪破壞劃分為非特定類(共62 組數據)，然后按照訓練集與測試集的比例為7∶3 將數據集進行分層隨機抽樣，最后以第二階段所遴選的最優特征參數a/h0、s/h0、 α1和 αv為輸入變量，利用94 組訓練集樣本(包括特定類51 組和非特定類43 組)，訓練第二階段邏輯回歸模型：

3.2 地震破壞模式判別的兩階段邏輯回歸模型

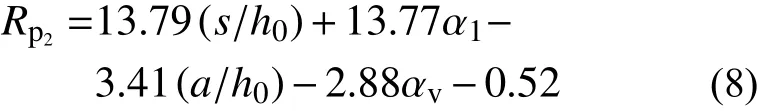
根據式(8)，當Rp2＜0時，表明RC 柱發生剪切破壞的概率小于彎剪破壞的概率，則判別RC 柱為彎剪破壞；當Rp2＞0時，表明RC 柱發生剪切破壞的概率大于彎剪破壞的概率，則判別RC 柱為剪切破壞。

需要說明的是，由式(7)和式(8)所建立的RC柱地震破壞模式兩階段邏輯回歸模型具有以下幾方面優勢：一是構建了RC 柱的特征參數與地震破壞模式之間的顯式函數關系，克服了傳統機器學習判別方法屬于“黑盒”模型，導致預測結果解釋性較差的缺陷；二是基于窮舉搜索策略，通過合理遴選最優特征參數，在保證判別準確度的前提下簡化了判別模型的函數形式，解決了傳統機器學習判別方法存在的判別模型復雜程度高、計算效率低的問題；三是在兩階段邏輯回歸模型的函數表達式中，其特征參數系數表征了各特征參數對地震破壞模式的影響程度。其中，系數的絕對值反映了影響程度的大小，而正負號則反映二者屬于正相關和負相關。

4 對比驗證分析

4.1 與經典邏輯回歸算法的對比分析

為驗證本文模型的有效性，選取經典邏輯回歸算法[15,17]進行對比分析。其中，經典邏輯回歸算法基于原始特征參數建立兩階段邏輯回歸判別模型(簡稱對比模型)，而本文模型基于最優特征參數建立兩階段邏輯回歸判別模型(簡稱本文模型)。根據上述第一階段和第二階段判別的訓練集樣本數據，分別建立兩個階段的對比模型，其特征參數系數取值見表2。由表2 可知，兩個階段的對比模型均與所有原始特征參數有關，所以兩個階段的對比模型均包含6 個特征參數，其判別模型的函數形式均有7 項，比式(7)和式(8)所描述的函數形式更加復雜。

表2 對比模型的模型參數取值Table 2 Model parameters of comparative models

根據訓練集建立的第一階段對比模型和本文模型，在測試集上的判別結果混淆矩陣如圖4 所示。圖4 中：F 表示彎曲破壞，FS 表示彎剪破壞，S 表示剪切破壞；混淆矩陣左上角2×2 矩陣中數字和百分比分別代表正確或錯誤判別樣本的個數和比例；混淆矩陣的最后一行和最后一列分別為精確度和召回率，前者表示每一類預測結果中正確預測的樣本所占的比例，后者表示每一類真實樣本中正確預測的樣本所占的比例，召回率和精確度越大，判別性能相對就越好，誤判的樣本就越少；混淆矩陣右下角的數字代表準確率，代表模型的總體判別準確度。由圖4 可知，對于彎曲破壞和非彎曲破壞，對比模型的正確判別數分別為33 和34，而本文模型的正確判別數分別為35 和38，說明對比模型對彎曲破壞和非彎曲破壞的樣本數均發生較多的誤判；對于彎曲破壞，對比模型的召回率和精確度均為82.5%，而本文模型的召回率和精確度分別為87.5%和92.1%；對于非彎曲破壞，對比模型的召回率和精確度均82.9%，而本文模型的召回率和精確度分別是92.7%和88.4%；由此可見，對于彎曲破壞和非彎曲破壞，本文模型的召回率和精度均明顯優于對比模型；同時，對比模型的總體判別準確率是82.7%，而本文模型的總體判別準確率是90.1%，比對比模型提高9%左右，說明本文模型具有較高的判別準確率。

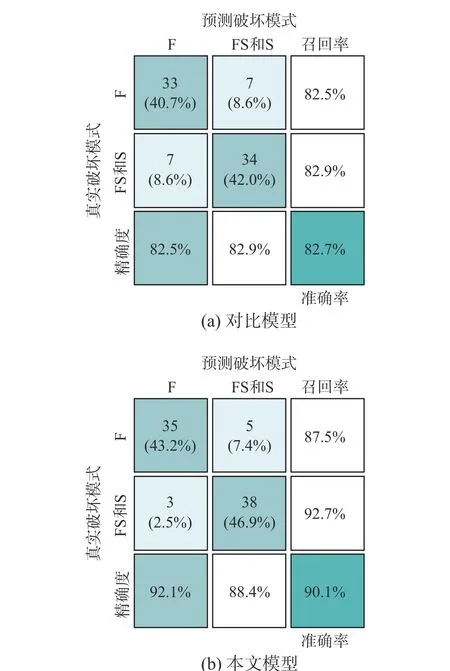
圖4 第一階段判別結果混淆矩陣Fig. 4 Confusion matrix of the 1st stage’s classification result

類似地，根據訓練集建立的第二階段本文模型和對比模型，在測試集上的判別結果混淆矩陣如圖5 所示。由圖5 可知，對于彎剪破壞和剪切破壞，對比模型的正確判別數分別為16 和19，而本文模型的正確判別數分別為16 和21，說明對比模型發生較多的誤判；對于彎剪破壞，對比模型的召回率和精確度均為84.2%，而本文模型的召回率和精確度分別為84.2%和94.1%，說明本文模型的精確度更高；對于剪切破壞，對比模型的召回率和精確度均為86.4%，而本文模型的召回率和精確度分別是95.5%和87.5%，說明本文模型的召回率和精度均較好；同時，對比模型的總體判別準確率是85.4%，而本文模型的總體判別準確率是90.2%，比對比模型提高5%左右，說明本文模型具有較高的判別準確率。

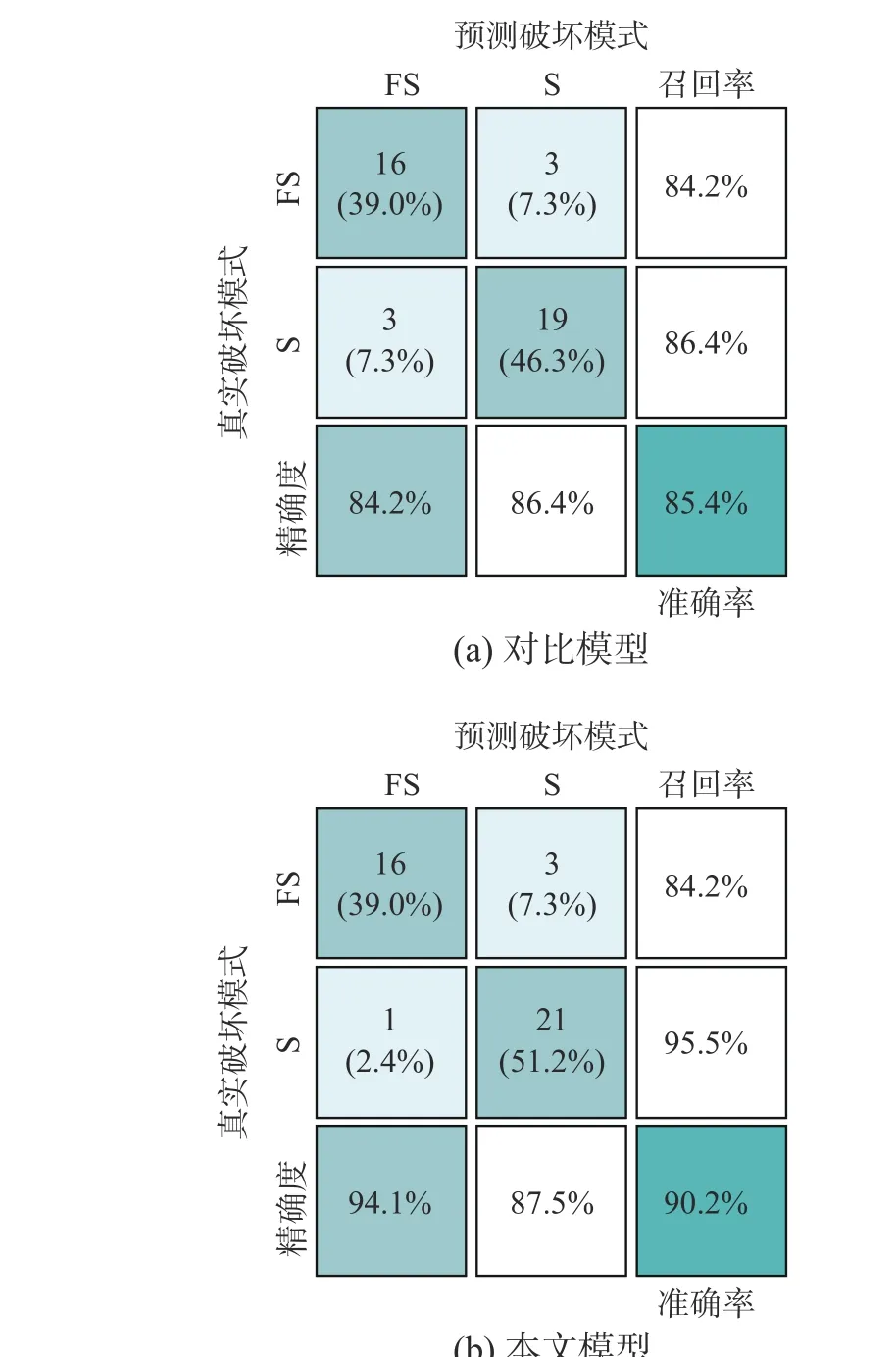
圖5 第二階段判別結果混淆矩陣Fig. 5 Confusion matrix of the 2nd stage’s classification result

為了進一步綜合對比分析本文模型和對比模型對于三種地震破壞模式的判別精度，計算三種地震破壞模式的F1值，見表3。其中，F1值定義為精確率P與召回率R的調和均值，綜合考慮了精確率和召回率的影響，F1值越大，說明判別精度越高。由表3 可知，對于彎曲破壞、彎剪破壞和剪切破壞，對比模型的F1值分別為0.83、0.84和0.86，而本文模型的F1值分別為0.90、0.89 和0.91，比對比模型均提高5%左右，說明對于三種地震破壞模式本文模型均具有更好的判別精度。

表3 RC 柱三種地震破壞模式的F1 值Table 3 F1 score of three failure modes for RC column

4.2 與傳統經驗判別方法的對比分析

下面通過與五種傳統經驗判別方法(見表4)進行對比分析，以驗證本文模型的有效性。對于所收集的270 組RC 柱地震破壞模式試驗數據，五種傳統經驗判別方法(分別記為CM1～CM5)與本文模型的判別結果混淆矩陣如圖6 所示。

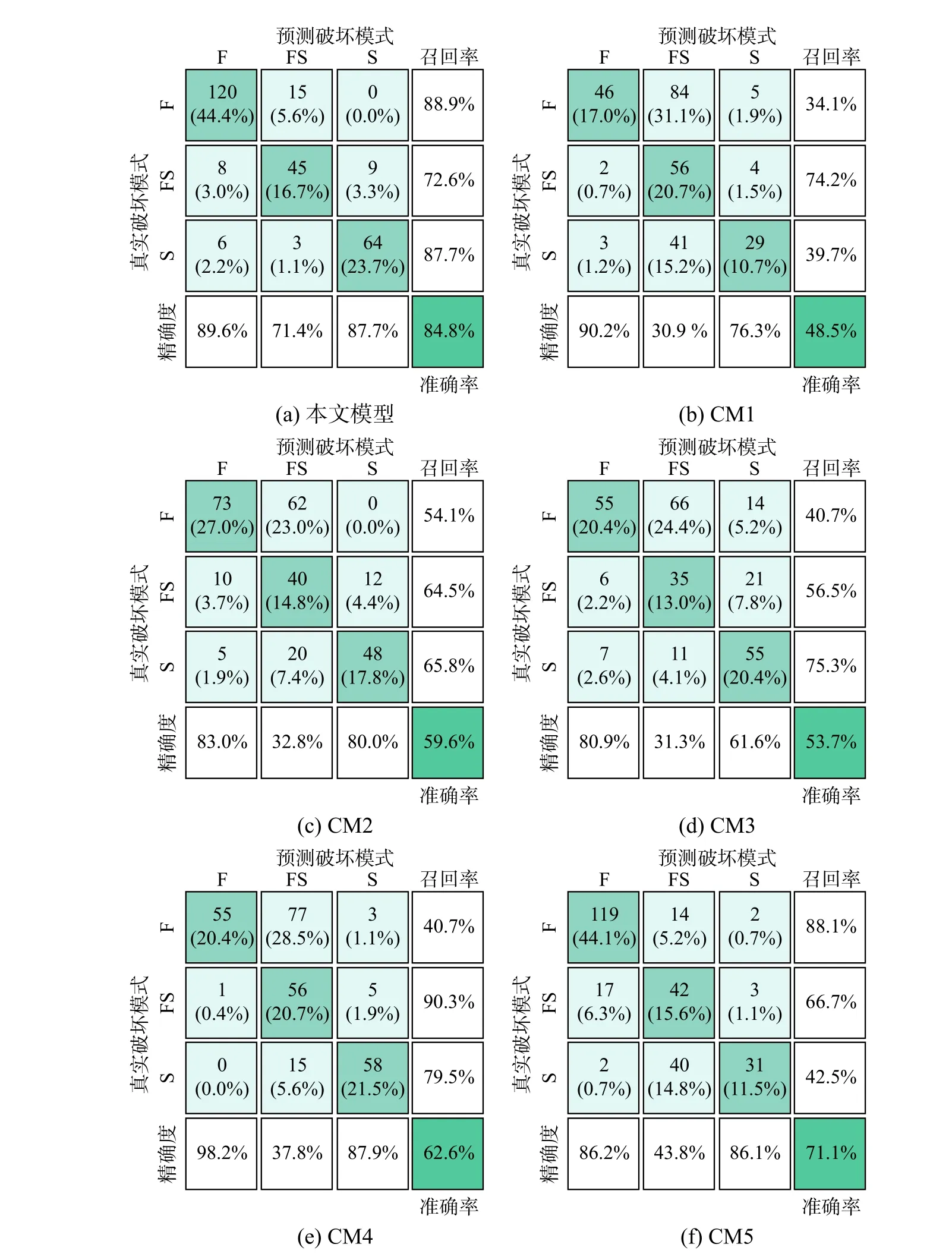
圖6 傳統經驗判別方法與本文模型的混淆矩陣Fig. 6 Confusion matrix of traditional empirical methods and proposed model

表4 五種傳統經驗判別方法Table 4 Five traditional empirical classification methods

由圖6(a)可知，本文模型對于彎曲破壞的正確判別率、召回率和精確度分別為44.4%、88.9%和89.6%，對于彎剪破壞的正確判別率、召回率和精確度分別為16.7%、72.6%和71.4%，對于剪切破壞的正確判別率、召回率和精確度分別為23.7%、87.7%和87.7%，模型的總體判別準確率是84.8%，說明本文模型對三種地震破壞模式的判別效果均較好，對彎曲破壞、剪切破壞和彎剪破壞的召回率和精確度分別達到89%、88%和72%左右，說明對三種地震破壞模式產生的誤判較少。由圖6(b)可知，判別方法CM1 對于彎曲破壞的正確判別率、召回率和精確度分別為17.0%、34.1%和90.2%，對于彎剪破壞的正確判別率、召回率和精確度分別為20.7%、74.2%和30.9%，對于剪切破壞的正確判別率、召回率和精確度分別為10.7%、39.7%和76.3%，模型的總體判別準確率是48.5%，說明判別方法CM1 對彎曲破壞和剪切破壞樣本的判別精確度相對較高，但是對彎剪破壞樣本的判別精確度只有30%左右，而且對彎曲破壞和剪切破壞的召回率均不到40%，較多的彎曲破壞或剪切破壞樣本被誤判為彎剪破壞。由圖6(c)可知，判別方法CM2 對于彎曲破壞的正確判別率、召回率和精確度分別為27.0%、54.1%和83.0%，對于彎剪破壞的正確判別率、召回率和精確度分別為14.8%、64.5%和32.8%，對于剪切破壞的正確判別率、召回率和精確度分別為17.8%、65.8%和80.0%，模型的總體判別準確率是59.6%，說明判別方法CM2對彎曲和剪切破壞樣本的判別精確度相對較高，但是對彎剪破壞樣本的判別精確度僅為35%左右，而且對三種地震破壞模式的召回率都僅有60%左右，說明每一類地震破壞模式中都存在較多的樣本被誤判。由圖6(d)可知，判別方法CM3 對于彎曲破壞的正確判別率、召回率和精確度分別為20.4%、40.7%和80.9%，對于彎剪破壞的正確判別率、召回率和精確度分別為13.0%、56.5%和31.3%，對于剪切破壞的正確判別率、召回率和精確度分別為20.4%、75.3%和61.1%，模型的總體判別準確率是53.7%，說明判別方法CM3 對彎曲破壞樣本的判別精確度相對較高，但對彎剪破壞和剪切破壞樣本的判別精確度都較低，分別為30%和60%左右，而且對彎曲破壞樣本的召回率僅有40.0%左右，說明較多的彎曲破壞樣本被誤判為彎剪破壞或剪切破壞，對彎剪破壞的召回率也僅有60%左右，較多的彎剪破壞樣本被誤判為彎曲破壞或剪切破壞。由圖6(e)可知，判別方法CM4 對于彎曲破壞的正確判別率、召回率和精確度分別為20.4%、40.7%和98.2%，對于彎剪破壞的正確判別率、召回率和精確度分別為20.7%、90.3%和37.8%，對于剪切破壞的正確判別率、召回率和精確度分別為21.5%、79.5%和87.9%，模型的總體判別準確率是62.6%，說明判別方法CM4對彎曲破壞和剪切破壞樣本的判別精確度相對較高，但對彎剪破壞樣本判別精確度較低，而且對彎曲破壞的召回率僅有40%左右，較多的彎曲破壞樣本被誤判為剪切破壞或彎剪破壞。由圖6(f)可知，判別方法CM5 對于彎曲破壞的正確判別率、召回率和精確度分別為44.1%、88.1%和86.2%，對于彎剪破壞的正確判別率、召回率和精確度分別為15.6%、66.7%和43.8%，對于剪切破壞的正確判別率、召回率和精確度分別為11.5%、42.5%和86.1%，模型的總體判別準確率是71.1%，說明判別方法CM5 對彎曲破壞和剪切樣本的判別精確度相對較高，但對彎剪破壞樣本的判別精確度較低，且對剪切破壞的召回率僅有40%左右，較多的剪切破壞樣本被誤判為彎曲破壞或彎剪破壞。

綜上所述，五種傳統的經驗判別方法無法兼顧三種地震破壞模式的召回率。根據判別精確度可知，存在較多的彎曲破壞和剪切破壞樣本被誤判為彎剪破壞，從而導致判別準確率較低；而本文模型對于三種地震破壞模式都具有較高的召回率和判別精確度，相較于五種傳統的經驗判別方法，總體判別準確率提高20%左右。

對于多分類問題，除了采用以上準確率、精確率和召回率等性能評價指標外，可采用統計學中評估多分類一致性的Kappa 系數[43]進行評估：

式中：Ka為Kappa 系數；po為與實際觀測一致的百分比，即準確率；pc為與理論期望一致的百分比，為每一類真實結果樣本數占樣本數的比例與預測結果樣本數占樣本數的比例的乘積之和。Ka的取值范圍為[0, 1]，其一致性評價標準[44]見表5。

表5 Kappa 系數一致性評價標準Table 5 Conformance evaluation criteria of Kappa coefficient

本文模型與五種傳統經驗判別方法的Ka值見表6。由表6 可知，判別方法CM1 和CM3 的Ka值分別為0.279 和0.328，均屬于[0.2, 0.4)區間取值范圍內，表明該兩種方法對三種地震破壞模式的判別效果較差，一致性等級評價較低，判別結果不具有實際參考價值；判別方法CM2、CM4和CM5 的Ka值分別為0.400、0.469 和0.539，屬于[0.4, 0.6)區間取值范圍內，表明該方法對三種地震破壞模式的判別準確率一般，一致性等級評價結果為中度一致性，判別結果具有一定的實際參考價值；本文模型的Ka值為0.757，屬于[0.6, 0.8)區間取值范圍內，表明本文方法預測結果大多數準確，一致性等級評價結果為高度一致性，具有較好的判別效果和實際參考價值。

表6 不同判別方法的Kappa 系數Table 6 Kappa coefficient of different classification methods

5 結論

基于窮舉搜索策略和邏輯回歸算法，提出了一種RC 柱地震破壞模式判別的兩階段邏輯回歸模型，并與傳統判別方法進行了對比。分析結果表明：

(1)基于窮舉搜索策略，遴選了RC 柱地震破壞模式的最優特征參數。其中，判別RC 柱發生彎曲破壞和非彎曲破壞的最優特征參數為Vp/Vn和軸壓比，判別RC 柱發生彎剪破壞和剪切破壞的最優特征參數為箍筋特征參數、縱筋特征參數、剪跨比和s/h0。

(2)對于RC 柱的三種地震破壞模式，本文模型對于三種地震破壞模式的判別準確率均達到90%以上，比經典邏輯回歸算法的準確率提高5%左右，比傳統經驗判別方法的判別準確率提高20%左右。

(3)本文模型不僅構建了特征參數與地震破壞模式之間的顯式函數關系，克服了傳統機器學習判別方法屬于“黑盒”模型，導致預測結果解釋性較差的缺陷，而且通過合理遴選最優特征參數，在保證判別準確度的前提下簡化了判別模型的函數形式，解決了傳統機器學習判別方法存在的判別模型復雜程度高、計算效率低的問題。

(4)需要說明的是，本文方法具有廣泛適用性，不僅適用于RC 柱的地震破壞模式判別，同樣也適用于其他三分類識別問題。