基于改進模型參考自適應的永磁輪轂電機無位置傳感器控制

李 勇，胡 晗，秦貞超，吳 浩，王文軍

（1.江蘇大學汽車工程研究院，鎮江 212013，中國；2.清華大學蘇州汽車研究院（吳江），蘇州 215200，中國；3.清華大學，汽車安全與節能國家重點實驗室，北京 100084，中國；4.北京特種機械研究所，北京 100143，中國）

分布式驅動用輪轂電機驅動系統由輪轂電機、驅動控制器及Hall 位置傳感器等部件組成，被安裝在有限的輪轂空間內，具有高度集成的特性，也賦予了其優越的性能[1-3]。但Hall 位置傳感器會受到路面沖擊、振動、電機溫升、逆變器死區等因素影響，導致其出現靈敏度變差、溫度漂移等問題，而且它的使用還會增加電機的體積、故障率及系統成本。因此，有必要對輪轂電機無位置傳感器控制進行研究，通過控制算法實現對輪轂電機轉子位置、速度等信息的軟測量，從而解決傳統位置傳感器的不足[4-7]。

無位置傳感器控制技術除了適用于零低速階段的凸極效應法，還包括適用于中高速階段的基波模型法[8-9]。永磁輪轂電機中高速運行狀態下的基波模型中包含有豐富的電壓、電流等信號，可通過基波模型法獲取輪轂電機轉速、位置信息。但是該方法對電機轉速十分依賴，且低速時反電動勢信噪比較低。目前研究較多的基波模型法主要有反電動勢（electromotive force,EMF）法、磁鏈法、狀態觀測器法、人工神經網絡法等。文獻[10]提出了一種EMF 積分控制方法，該方法不依賴于電機的轉速，但需要進行數據積分，增加了積分誤差。文獻[11]提出了一種“主動磁鏈”的概念，將轉子凸極轉化為隱極具有較寬有效轉速區間。該方法不依賴于轉速，但需要考慮電壓信號中的噪聲影響，計算量較大。文獻[12]研究了一種支持向量機回歸觀測器方法,基于擾動觀測器理論通過EMF 觀測值估計出轉子位置。該機制實現簡單，不需要狀態向量推導，能夠解決電機在高速重載下難以估算的問題，具有較強的魯棒性，但需要進行大量運算。文獻[13]設計使用徑向基方程神經網絡法完成參數估算，利用遞推最小二乘法設計網絡的連接權，在線訓練得到轉子角度的觀測值。該方法具有較強的自適應和自學習的特點，但對網絡模型依賴較高，不能保證辨識結果的準確性。

模型參考自適應(model reference adaptive system,MRAS)在20 世紀50 年代由美國科學家Whitaker 提出，最初是用來作為飛行器的控制策略，可以適應于非線性、多變量復雜系統的控制。自適應系統具有自我修正以逼近目標的特性，具有較強的抗擾動能力[14-15]。傳統MRAS 控制器在有精確模型的線性控制中能夠發揮出色的性能，但這種固定增益線性求和函數的輸出效果并不盡如人意。電動汽車電機驅動系統需要工作在變負載、寬轉速范圍工況下，具有嚴重非線性特性。傳統MRAS 的反饋環節是一種通過線性加權形式得到的固定增益反饋回路，只能在一定的負載范圍與轉速范圍內才能穩定得到較為準確的估算結構[16]。

本文在上述算法優缺點基礎上，借鑒自抗擾控制理論，利用具有非線性結構的fal 函數，對傳統固定增益的模型參考自適應律進行改進，構建具有變增益非線性特性的模型參考自適應律[17-18]，提出了一種基于改進模型參考自適應(improved model reference adaptive system，IMRAS)的永磁輪轂電機無位置傳感器控制方法；重點研究了不同工況下IMRAS 無感控制算法的魯棒性與抗干擾能力；同時將IMRAS 無傳感器控制方法與傳統MRAS 法進行了仿真對比驗證，最后又利用雙電機對拖實驗平臺進行了臺架實驗驗證。

1 永磁輪轂電機數學模型

由于永磁輪轂電機具有較強的非線性、強耦合特性，需進行以下簡化分析：忽略鐵芯磁路飽和，忽略空間諧波，認為三相繞組完全對稱，電動勢為標準正弦波。在旋轉坐標系（d/q坐標系）下，輪轂電機的動態電壓方程為[19-20]：

其中：ud、uq分別為定子電壓的d/q分量；id、iq分別為定子電流的d/q分量；ψd、ψq分別為永磁磁鏈的d/q分量；p為微分算子；Rs為定子電樞電阻；ωe為電角速度。

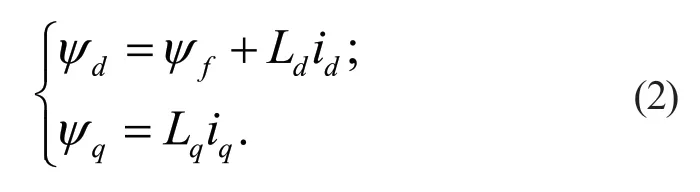
其中：Ld、Lq分別為d、q軸電感；ψf為轉子永磁磁鏈。將式(2)代入式(1)，可得：

2 基于IMRAS 的輪轂電機無位置傳感器控制

2.1 傳統固定增益自適應律的MRAS 設計

采用MRAS 算法實現永磁輪轂電機轉速及位置的無傳感器估算，其基本思想是將不包含位置信息的電機數學模型作為參考模型，并建立含有待估計參數的可調模型，利用兩模型輸出的偏差設計反饋回路和自適應律。在系統運行過程中，不斷采集系統狀態參數，通過比較系統狀態變量與控制變量確定系統狀態，建立自適應律，不斷地進行前饋或反饋調節，從而達到使兩模型輸出之間誤差調節至零，可調模型的待辨識參數便可以收斂到準確實際值的目的[21]。基于MRAS的轉速與轉子位置辨識框圖如圖1 所示。

圖1 基于MRAS 的轉子速度與位置辨識框圖

無論是基于電流模型還是磁鏈模型，其實現原理一致。但基于磁鏈模型可以省去變換環節，優化計算步驟。

根據式(1)和式(2)所示數學模型，可得磁鏈模型：

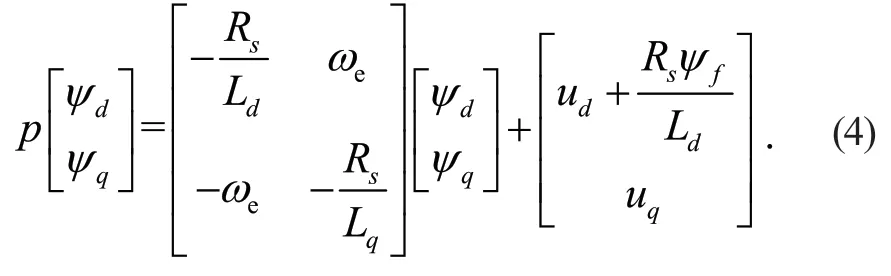
以式(4)作為參考模型，將系統狀態變量的估計值代入，則可得到可調模型為：

將上述基于磁鏈模型選定的參考模型和可調模型作差可得關于定子磁鏈的誤差狀態方程，如下:

改寫成如下形式：

根據式(7)，定子磁鏈的誤差系統的狀態方程可轉換為以下形式：

其中，C為增益矩陣。為簡化計算，通常取C=I，I為單位矩陣，則此時v等于磁鏈誤差矢量eψs。

非線性時變系統框圖如圖2 所示。

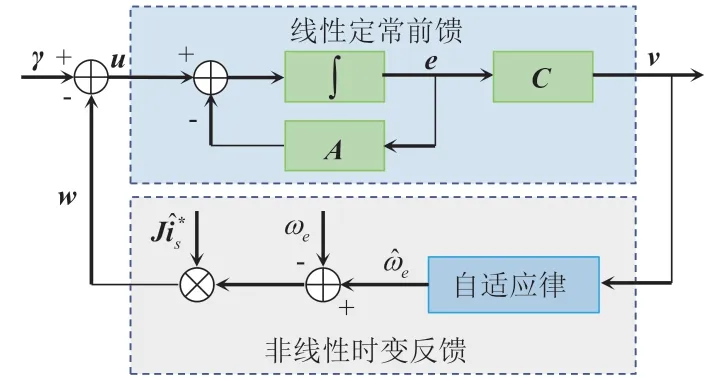
圖2 非線性時變系統框圖

至此開始自適應律的設計，一般Popov 超穩定性理論通過對Popov 積分不等式逆向求解得到穩定可靠的系統自適應律。根據Popov 穩定判據，系統的穩定性證明要同時符合如下條件：

(1) 傳遞函數矩陣H(s)=C（sI-A）-1為正定矩陣；

(2) 在反饋回路中，滿足不等式：

基于正實引理，很容易求得當C=I時，傳遞函數矩陣H(s)=C（sI-A）-1滿足嚴格正定條件。

采用傳統自適應律，將估計轉速的表達式如下所示：

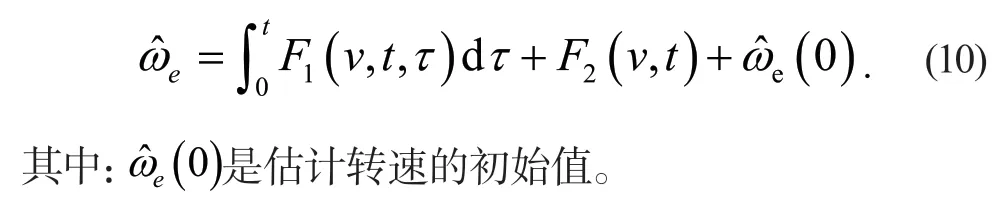
將式(10)代入式(9)，可得估算轉速表達式：

經推導，當滿足式(12)和式(13)時，所構建傳統自適應律滿足Popov 超穩性定理。

將式(12)和式(13)代入式(10)，可得估算轉速表達式(14)：

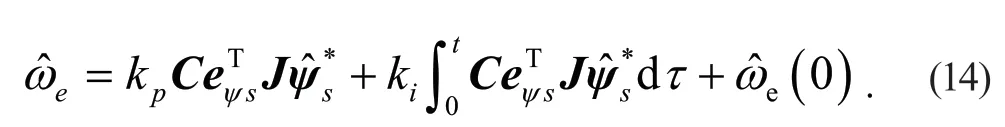
采用傳統反饋系統構建的自適應律如式(15)所示：

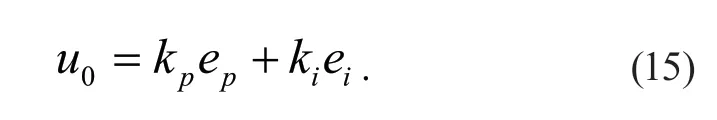
其中：ep為偏差的比例項；ei為偏差的積分項；kp、ki為自適應系統的可調系數。

傳統反饋系統是一種通過線性加權形式得到的固定增益反饋回路，只能在一定的負載范圍與轉速范圍內才能穩定得到較為準確的估算結構。

2.2 基于fal 函數的改進自適應律的MRAS 設計

為了對傳統固定增益的控制器進行改進，應用自抗擾控制理論，利用具有非線性結構的fal 函數，構建具有變增益非線性特性的自適應律。如式（16）所示：

其中：kp、ki為自適應系統的可調系數，其中非線性結構的fal 函數式(17)所示：

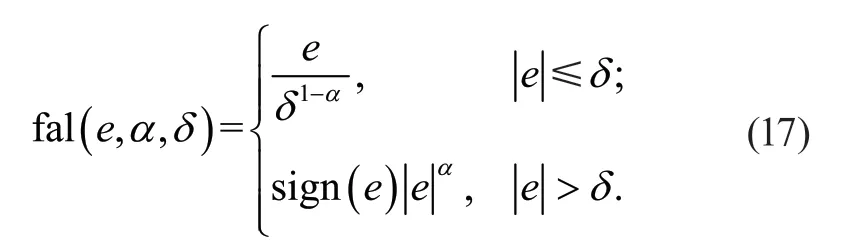
其中：sign(x)為符號函數；α為取值0～1 之間的常數；δ為影響濾波效果的常數。

當|e| ≤δ時，自適應系統的收斂機制與傳統自適應控制一致，此時系統符合Popov 穩定性條件。當|e|＞δ時，誤差系統呈現冪函數形式，α的取值范圍為[0,1]，估計轉速的自適應率表達式為：

令

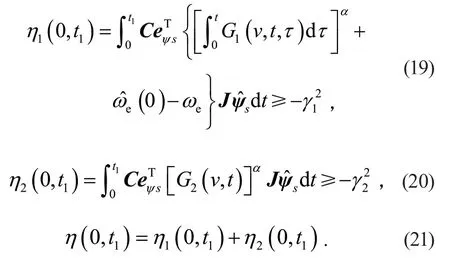
取

假設

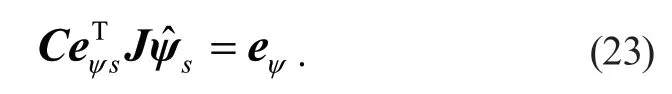
當eφ＞δ時，將式（22）和（23）代入式（19），可得

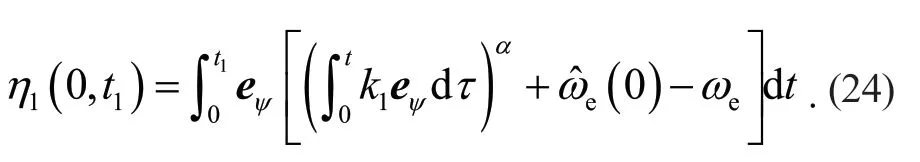
構造一個函數f(t)滿足

其中k＞ 0，將式（25）代入式（24），可得：

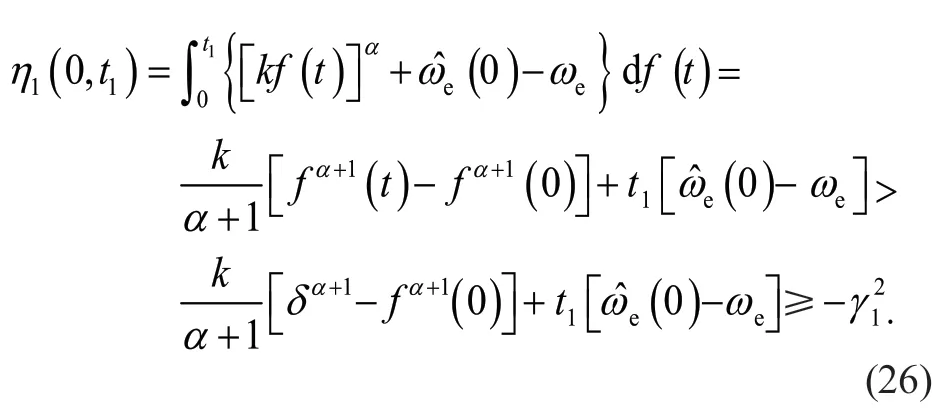
同理，取

代入式（20），得：

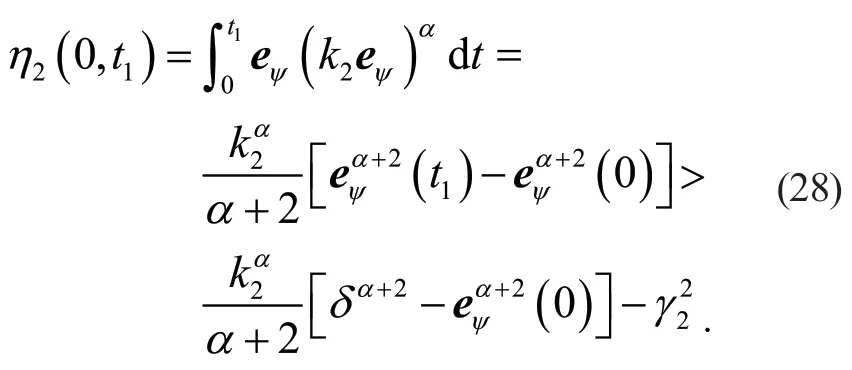
綜上所述，本文設計的基于非線性PID 的自適應律符合Popov 穩定性定理，則磁鏈誤差方程為：

參考模型為基于電流輸入，可調模型為基于電壓輸入，估算轉速表達式為：

轉子位置電角度θe可通過對轉速進行積分獲得：

3 系統仿真及結果分析

3.1 仿真搭建

結合矢量控制技術和MRAS 轉速辨識的數學模型，建立基于MRAS 方法的永磁輪轂電機無位置傳感器矢量控制仿真模型，其結構框圖如圖3 所示。在傳統MRAS 方法的輪轂電機無位置傳感器矢量控制基礎上，將固定增益的自適應律改為基于fal 函數的變增益自適應律，即可完成IMRAS 轉速估算模塊的建立。對建立的2 種模型進行負載突變與轉速突變工況下的仿真及分析。

圖3 基于MRAS 的無位置傳感器矢量控制結構框圖

3.2 仿真結果分析

3.2.1 負載突變工況仿真結果

圖4 所示為不同負載下的永磁輪轂電機無位置傳感器矢量控制仿真結果。可以看出，傳統MRAS 估算策略能較好地在負載突變以及不同負載工況下完成轉速跟蹤，但是在大負載突變工況下跟蹤效果會變差，伴隨著一定的抖動出現。500 r/min 轉速運行時傳統MRAS 方法能夠保證轉速估算誤差在±3 r/min 范圍，空載或低負載下1 000 r/min 轉速運行能夠保證轉速估算誤差在±5 r/min 范圍。負載突變時，轉速估算誤差有一個激增，但幅度不大。從2 個轉速的估算誤差對比，可以看出輪轂電機高速運行時，隨負載增加轉速估算誤差也會增大。從圖4e 與圖4f 的傳統電磁轉矩響應曲線可以看出，轉速較大，電磁響應轉矩脈動幅度也較大，同時隨著負載的增大電磁響應轉矩脈動幅度也隨之有小幅度的增大;但在高速、大負載時電磁響應轉矩脈動幅度增大較明顯，幅值約有10 Nm。改進后的MRAS 估算策略能很好地應對負載的變化。從圖4c 與圖4d 可以看出，在負載突變時，轉速估算誤差仍存在激增現象，但相比于傳統MRAS 方法，隨負載增加轉速估算誤差基本保持不變，即IMRAS 能夠更好地適應負載變化環境。圖7e 與圖7f 分別為轉速500 r/min 和轉速1 000 r/min 的電磁轉矩響應曲線，隨轉速增大電磁轉矩脈動幅度仍會有小幅增大，但在較高轉速、大負載下的電磁轉矩脈動幅度相較于傳統算法下有明顯的縮小，約為5 Nm。

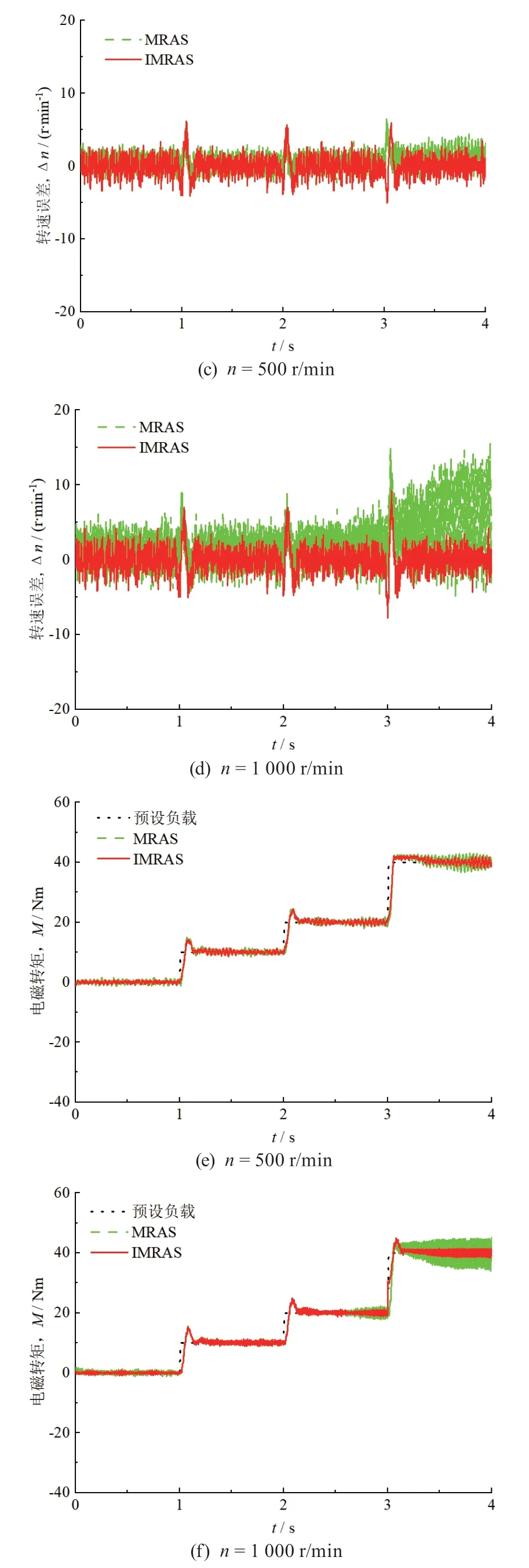
圖4 不同負載下的永磁輪轂電機無位置傳感器矢量控制仿真結果

3.2.2 轉速突變工況仿真結果

圖5、圖6 所示為不同轉速下的永磁輪轂電機無位置傳感器矢量控制仿真結果。從圖5a 可以看出，傳統MRAS 估算策略在低速區無法準確獲取轉速信息，中高速下能夠較好的完成轉速估算，切換節點在370 r/min 左右，位置估算的跟蹤收斂情況如圖5b 所示。從圖5c 可以看出，在低速區域估算位置與實際位置幾乎無偏差，高速區域估算轉子位置產生了一定程度的偏移。從圖5d 可以看出，低速階段轉速變化過程中估算誤差基本不變，轉速達到1 000 r/min 之上時，轉速變化過程中估算誤差增大，且隨著轉速的增加估算誤差也會有所增大。從圖5e 可以看出在中低速區間估算誤差能夠保持在±2°以內，在高速區轉速切換過程中估算誤差明顯增大，且轉速過高時轉子位置估算誤差增大到±4°左右。相比于傳統MRAS 估算策略，從圖6a 可以看出，轉速估算有效工作的轉速范圍有所拓展，轉速節點從370 r/min 左右降低至260 r/min 左右，位置估算的跟蹤收斂情況如圖8b 所示。從圖8c 可以看出位置估算結果較為準確。從圖8d 可以看出，從低速階段到高速階段，轉速估算誤差無明顯變化。轉速變化過程中估算誤差會有所增加，但均保持的±4 r/min 以內。從圖8e 可以看出，隨轉速增加估算誤差仍會有所增加，且轉速變化過程中估算誤差也較穩定車速時增大，但相比于傳統MRAS 有所改善，估算誤差在±3°以內。

圖5 不同轉速下的永磁輪轂電機傳統無位置傳感器矢量控制仿真結果

圖6 不同轉速下的永磁輪轂電機改進無位置傳感器矢量控制仿真結果

圖7 實驗臺架實物圖

綜合上述分析，相比于傳統MRAS 轉速估算策略，采用非線性變增益自適應律改進后的IMRAS 轉速估算算法具有更寬的有效工作的轉速區間，且能夠更好地適應寬范圍轉速變化與寬范圍負載變化的復雜工況。

4 實驗及結果分析

4.1 實驗平臺搭建

通過搭建雙電機對拖實驗臺架，完成對本文所提出的無位置傳感器控制方法的實驗驗證。實驗臺架由驅動電機和負載電機組成。電機控制系統采用強電與弱電獨立分開設計：驅動板為強電部分，包括整流電路、逆變電路和電流和電壓采樣電路；控制板為弱電部分，搭載TMS320F28335 型號DSP 芯片作為主控芯片，實現信號采集、算法實現以及脈沖寬度調制(pulse width modulation，PWM）信號輸出等功能。驅動系統通過CCS（Code Composer Studio）環境載入基于MRAS 的無傳感器矢量控制程序，可通過串口與上位機進行通信，向上位機發送電流、轉速等信息。加載系統內載入轉矩輸出程序，可在上位機選擇轉矩數據并通過串口輸入加載控制系統。實驗臺架實物圖如圖9 所示。驅動電機參數如表1 所示。

表1 電機參數

4.2 實驗結果分析

通過實驗臺架分別進行了負載突變工況、轉速突變工況以及中國汽車測試循環(China automotive testing cycle,CATC) 測試工況下的試驗。

4.2.1 負載突變工況實驗結果

圖8 為初始轉速500 r/min 情況下突變負載實驗結果，在0.8 s 時輸入一個幅值為1 Nm 的階躍轉矩。從圖8a 可以看出2 種方法在轉矩突變階段都會產生較大的估算誤差，但IMRAS 方法的相對誤差較小。施加的階躍轉矩會使電機轉速下降，但采用IMRAS 方法電機轉速回升時間相比于傳統方法更短一些，說明轉速估算的準確性影響電機的轉矩響應與輸出性能，即估算精度影響驅動控制系統的穩定性與可靠性。從圖8b 可以看出施加轉矩前后，IMRAS 方法的轉速估算誤差幾乎沒有差別，而施加轉矩后傳統方法的估算誤差有所增加。

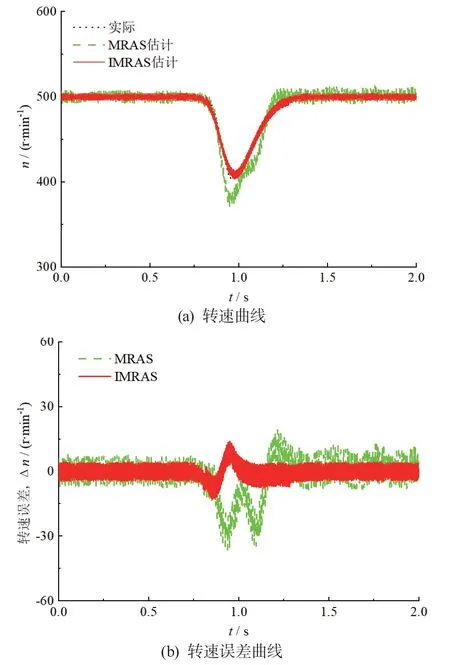
圖8 初始轉速500 r/min 突變負載實驗結果

圖9 為初始轉速1 000 r/min 情況下突變負載實驗結果，在0.8 s 時輸入一個幅值為1 Nm 的階躍轉矩。從圖9a 可以看出，IMRAS 方法的轉速下降幅度更小，轉速回升時間更短，傳統方法估算轉速曲線的抖動更大。對比圖9b，傳統MRAS 方法的估算誤差大于IMRAS 方法。在轉矩變化階段，2 種方法的估算誤差都有所增大，但傳統方法的估算誤差增幅更大。負載增加后，傳統MRAS 方法的估算誤差有所增大，而IMRAS 方法的估算誤差幾乎不變。可見IMRAS 方法有更強的適應變化負載的能力。對比圖8 和圖9,1 000 r/min 轉速下傳統MRAS 的估算誤差大于500 r/min 時的估算誤差。而IMRAS 方法估算誤差增加并不明顯。

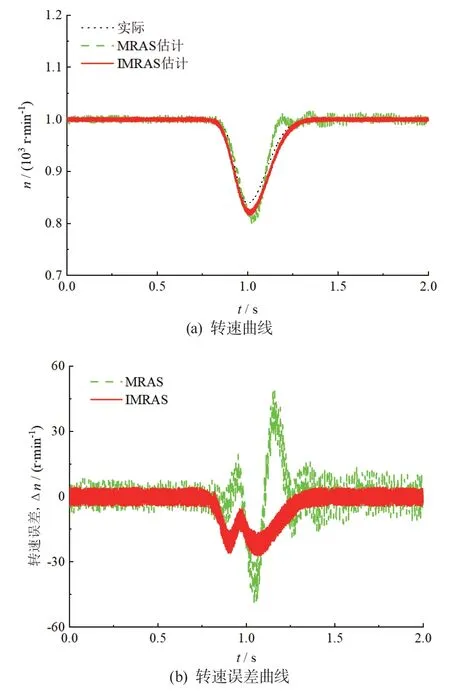
圖9 初始轉速1 000 r/min 突變負載實驗結果

4.2.2 轉速突變工況實驗結果

圖10 為空載情況下突變轉速實驗結果，在0.8 s時轉速由500 r/min 突增至600 r/min。從圖10a 可以看出2 種方法在轉速變化階段都會產生較大的估算誤差，但IMRAS 方法相對誤差較小，估算轉速跟蹤實際轉速更加準確且穩定。對比圖10b 轉速變化前后，IMRAS 方法的轉速估算誤差幾乎沒有差別，而施加轉矩后傳統MRAS 方法的估算誤差稍有增加，可見隨著轉速增加，傳統方法的估算誤差有所增加。

圖11 所示實驗結果的實驗條件為：驅動電機初始施加1 Nm 負載，在0.8 s 時轉速由500 r/min 突增至600 r/min。對比圖11a 可以看出，IMRAS 方法的轉速跟蹤效果更好，速度上升更快，傳統方法估算轉速曲線的抖動更大。對比圖13b 傳統方法的估算誤差大于IMRAS 方法。在轉速變化階段，2 種方法的估算誤差都有所增大，但傳統方法的估算誤差增幅更大。轉速上升后，傳統方法的估算誤差進一步增大，而IMRAS方法的估算誤差幾乎不變。可見IMRAS 方法有更強的適應變化轉速的能力。對比圖10 和圖11,帶載情況下傳統方法的估算誤差大于空載時的估算誤差。而IMRAS 方法估算誤差增加并不明顯。

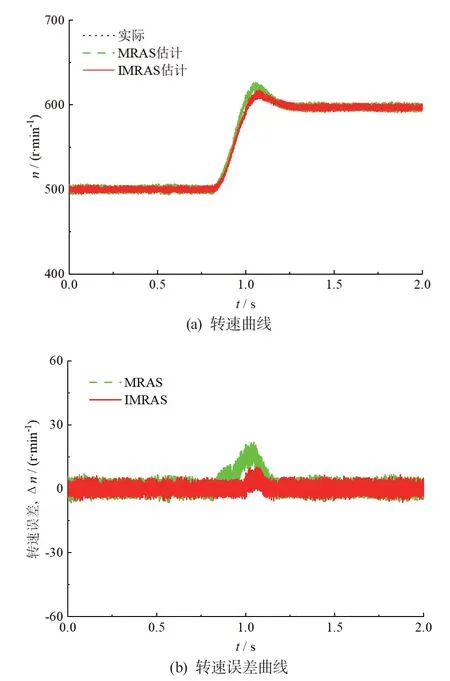
圖10 初始空載下突變轉速實驗結果

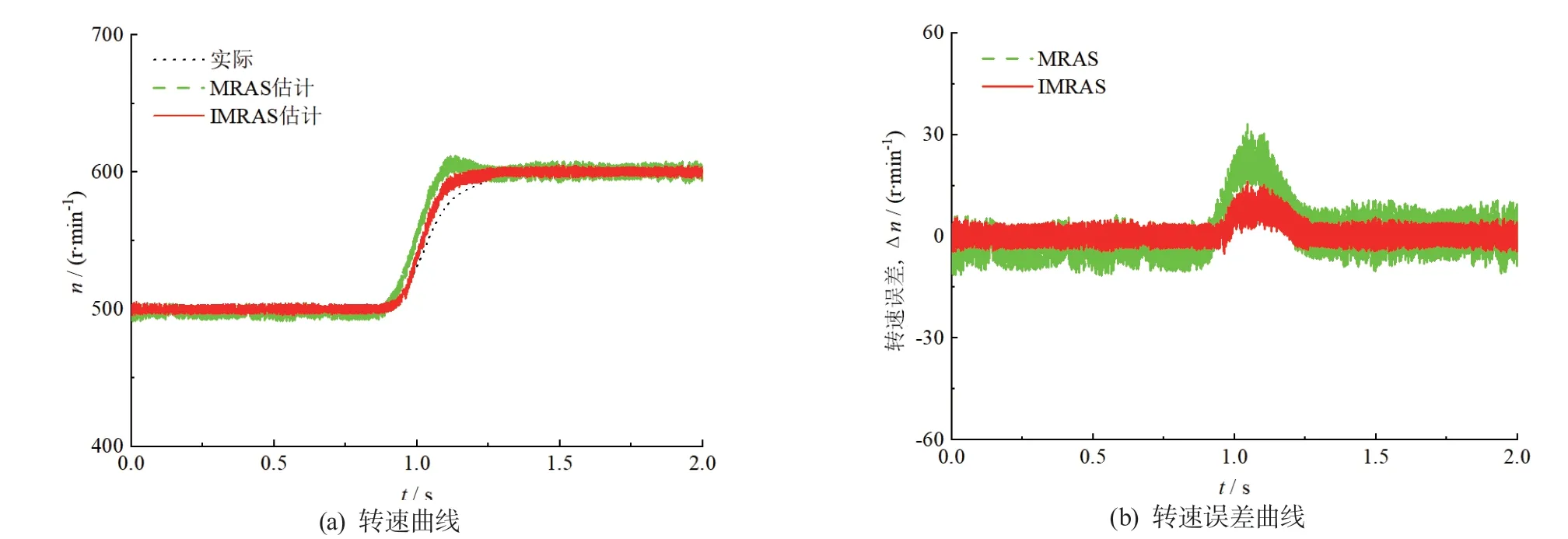
圖11 初始帶載下突變轉速實驗結果

4.2.3 CATC 循環工況實驗結果

圖12a 為CATC 循環工況下的輪轂電機轉速反饋曲線。由于MRAS 算法僅適應于中高速階段，初始階段系統利用傳統霍爾傳感器完成電機加速，到達設定的200 r/min 轉速閾值后切換至無位置傳感器控制模式。雖然轉速估算結果隨著電機轉速和負載的動態變化產生一定范圍的波動，在高速階段與轉矩突變階段波動稍有增加，但不影響電機的運行，該控制算法能夠很好的適應轉速與負載同時變化的輪轂電機運行工況。在400 s 之后電機轉速下降，結合圖12b 所示的負載電機的轉矩指令與轉矩反饋曲線，可見該階段電機失去轉矩輸出能力，但中高速階段電機的轉矩跟蹤效果較好，轉矩響應較迅速。圖12c 為電機的某一時間內三相電流響應曲線。可以看出，在空間電壓脈沖寬度調制模塊的控制下，三相電流具有較好的正弦特性。

圖12 循環工況測試實驗結果

綜合以上結果分析可得，本文提出的IMRAS 轉速估算方法對轉速變化、負載變化具有較好的適應性，能夠較好地實現永磁輪轂電機在中高速階段的無位置傳感器控制。

5 結論

本文提出了基于改進模型參考自適應(IMRAS)的電動汽車用永磁輪轂電機無位置傳感器控制策略，采用fal 函數設計了變增益模型參考自適應律，代替了傳統的固定增益模型參考自適應律，建立了基于IMRAS算法的永磁輪轂電機無位置傳感器矢量控制模型。結果表明：與傳統模型參考自適應(MRAS)算法相比，所設計的IMRAS 算法在負載突變與高轉速運行工況下有明顯的穩定性和抗干擾能力;以中國汽車測試循環(CATC)工況為參考轉速，驗證了本文所提出的IMRAS 方法能夠很好地適應變速變載運行工況，具有良好的無位置傳感器控制特性。