動量定理在Unity 3D中的應用

丁彥希，張迪迪，徐秋雨，郭仁春

（沈陽化工大學，遼寧 沈陽 110142）

0 引 言

動量定理是動力學的普遍定理之一。剛體是力學中的一個科學抽象概念，即理想模型。Unity 3D簡稱U3D，是由Unity Technologies公司開發的一個讓玩家輕松創建諸如三維視頻游戲、建筑可視化、實時三維動畫等類型互動內容的多平臺的綜合型游戲開發工具。在U3D中，是通過物理引擎機制來實現物體的物理效果。物理引擎通過為剛性物體賦予物理屬性的方式來模仿真實世界中的物體碰撞、跌落等反應。本文通過給剛體添加力和力矩來使剛體產生運動，包括平動和轉動，并對運動狀態進行定量分析，使讀者能更好的認識動量定理在剛體運動中的體現，從而更好地設計一個仿真系統。

1 剛體運動——從剛體平動到剛體轉動

1.1 牛頓定律和動量定理

剛體都有質心的概念，如果作用力的方向通過質心，則可以將剛體視作質點。當剛體的作用力不在質心上時，剛體會發生轉動，轉動時所有的物理量和物理定律都可以從平動形式類推過來。

剛體平動用位移，速度，加速度，慣性，力，動量，沖量等描述，對應的剛體轉動要換成角位移，角速度，角加速度，轉動慣量，力矩，角動量，角沖量等概念，所有的物理定律都不變，如表1所示。

表1 剛體平動與剛體轉動物理量對比

1.1.1 平動慣性定律和轉動慣性定律

牛頓第一定律也叫慣性定律，慣性是物體要保持原有的狀態。慣性是有大小的。物體的質量mass就是衡量慣性的一個重要指標。

轉動時，物體要保持勻速旋轉的狀態，即保持角速度大小和方向不變，這就是轉動慣性定律。轉動慣性也有大小，用轉動慣量來衡量。轉動慣量用I來表示，其定義為

其中是質量，是該質心的位置到轉軸的距離，的單位是kgm。

1.1.2 平動牛頓第二定律和轉動牛頓第二定律

如果要改變狀態就需要外力。外力越大狀態改變也越大，但如果慣性即質量很大，狀態改變就越小。用數學公式來描述即

這就是牛頓第二定律，其中是慣性，是外力，是加速度。

如果要改變轉動的狀態，即改變角速度，就需要對剛體加外力矩，因此角速度的改變用角加速度來衡量，該值與外力矩大小成正比，與轉動慣量成反比，這與加速度的定義極為相似，即：

1.1.3 平動動量定理和轉動動量定理

平動過程中的動量是，轉動過程中的角動量是。平動的動量定理和轉動的角動量定理分別為：

1.1.4 動量守恒和角動量守恒

當兩個物體相互碰撞后，在沒有損耗的情況下，碰撞前的總動量=碰撞后的總動量，這就是動量守恒。與平動相似，角動量也滿足守恒定律。如果兩個剛體相碰撞，兩者相比較如下：

這些定律都體現在U3D的物理引擎中，了解這些物理定律就會讓虛擬仿真更符合的預期。

1.2 剛體屬性

在場景中放置一個平面Plane作為地面，再添加一個立方體Cube和一個球體，并讓這兩個物體位于地面上方如圖1（a）所示。給立方體和球體增加剛體組件RigidBody如圖1（b）所示。運行后物體會自動落到地面。

圖1 Rigidbody組件

讓場景中的物體運動可以有兩種方式，其一是運動學，其二是用物理學。

運動學使用的是物體的Transform，直接用Translate（平移）和旋轉（Rotate）來使物體移動或旋轉，或者直接用代碼改變物體的位置和歐拉角。

場景中的物體加載了Rigidbody組件，就要受到物理定律的控制，如果希望不被物理定律控制，可以開啟該組件中的Is Kinematic選項。

與物理問題相關的程序要寫在FixedUpdate中，FixedUpdate兩幀之間的間隔是固定的，默認是0.02 s，也就是1秒鐘運行50次。這與Update不同，Update兩幀之間的間隔是不固定的。

質量mass（kg），速度velocity（m/s）是剛體的兩個基本屬性，一個代表慣性，一個代表狀態。在剛體的眾多屬性中最重要的就是速度velocity了，而mass多數時候可以忽略。

2 轉動慣量inertiaTensor

對于平動，剛體有一個慣性量就是質量mass，同樣對于轉動，剛體也有一個描述轉動慣性的量，叫作慣性張量inertiaTensor。

轉動慣量除了與質量相關外還與旋轉軸位置、剛體形狀和大小有關。同一個剛體旋轉軸的位置，有不同的轉動慣量。若旋轉軸通過剛體的質心，軸的方向不同，也會有不同的轉動慣量，其中沿著物體坐標系，，主軸的三個方向的轉動慣量最為重要，其次是其他方向，這樣的轉動慣量共有9個參數形成一個張量矩陣如下：

，，主軸方向上的量處于矩陣的對角線上，即I，I和I。在U3D中，慣性張量inertiaTensor就是指這三個數，形成一個向量。

3 AddForce

將場景中物體的質量mass設為2 kg，給剛體施加一個沿軸方向500 N的力的代碼如下：

其中，rb是指如圖1所示場景中的物體。

像平時扔東西，擊球或開槍都是給物體一個初始的力，然后物體就沿力的方向前進了。但同樣是給物體一個水平方向500 N的力，瞬間給一下，持續一段時間和一直持續給，物體速度很顯然是完全不同的。如下文給出的代碼所示：

其中AddForce代碼只在Start()中僅加載一次，AddForce是對物體加力，這個力的作用時間Δ其實就是0.02 s，也就是FixedUpdate兩幀之間的間隔Fixed Timestep。

根據動量定理求出：

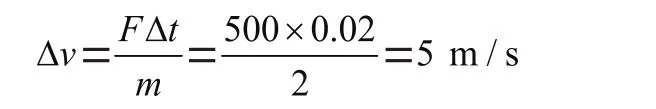
U3D中對AddForce提供了四種模式，用ForceMode來區別，方法是對AddForce增加第2個參數：

rb.AddForce(new Vector3(500, 0, 0), ForceMode.Force);

ForceMode的四種模式分別是：Acceleration、Force、Impulse、VelocityChange，其力的作用方式有些區別，默認是Force，可以省略。

3.1 Force

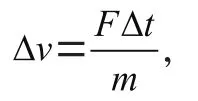
3.2 Acceleration

Acceleration是加速度，單位是m/s，加速度本身就是速度的改變量，因此下面的代碼：

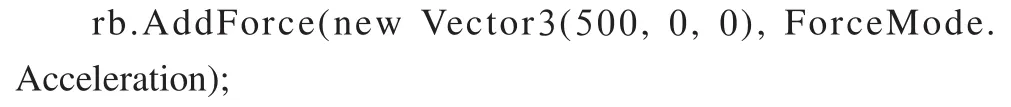
可以猜測得到物體的速度應為：10 m/s

因為加速度=500 m/s，說明速度1秒增加500 m，因而作用時間是0.02 s，最終速度自然就是500×0.02=10 m/s。

由于直接使用的是加速度，就不用考慮物體質量了。

3.3 Impulse

Impulse是沖量，單位是N?s或者kg?m/s，該量就是直接給了Δ。因此下面的代碼：

rb.AddForce(new Vector3(500, 0, 0), ForceMode.Impulse);

可以猜測到物體的速度為：

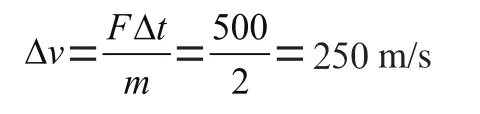
由于直接給的是沖量，這樣就不用考慮作用時間0.02 s了。因此Impulse應該是每次運行就施加500 N?s，與作用時間無關，只考慮運行次數即可。

3.4 VelocityChange

VelocityChange 顧名思義是速度的改變量，這樣的說法有點類似Acceleration，與Acceleration不同的是，VelocityChange是每次運行就改變速度的量，而Acceleration則是每秒速度的改變量。因此VelocityChange的單位應該是米/秒/次。

因此代碼：

運行結果就應該是：500 m/s

VelocityChange與Acceleration一樣不用考慮物體的質量。VelocityChange與Inmpuse一樣不用考慮那個時間間隔。

通過這幾個例子可以看到velocity才是最想知道的量，而mass常被忽略。

4 AddTorque

4.1 給立方體加力矩

與AddForce相似，可以給物體施加力矩AddTorque，該力矩可以使剛體繞質心旋轉。如果外力矩為，則剛體的角速度的變化量為：

在U3D中Δ=0.02 s，為轉動慣量，這個轉動慣量為慣性張量inertiaTensor，由于是張量，問題就變得比平動復雜得多，下面依然采用手工計算與代碼相結合的形式進行相互驗證。

對場景中的立方體編寫下文的代碼：

因此結果應該是（1.2，0，0）。運行后發現正是這個結果如圖2所示。

圖2 給立方體加力矩后的運行結果

4.2 給長方體加力矩

通過代碼驗證，結果如圖3所示。

圖3 長方體的轉動慣量運行結果

下面將長方體斜著放置，力矩仍保持不變，將立方體的歐拉角設為（0，30，0），如圖4（a）所示是頂視圖。現在給一個力矩=(10，0，0)，這個力矩是對世界坐標系的而言的。那么認為物體應該繞世界坐標x軸旋轉，即如圖4（b）所示的那個樣子，繞紅色軸旋轉。

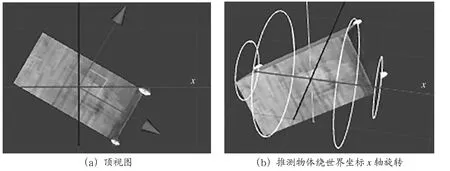
圖4 斜長方體方體轉

然而運行結果卻是另外的形式，轉軸相對世界坐標發生了偏移，其角速度如圖5所示。

圖5 運行結果

如圖6（a）所示，物體是繞著黃色的軸旋轉的，不是紅色的軸

圖6 對x軸加力矩，結果旋轉軸發生偏移

如果再將歐拉角改成（0，60，0），結果如圖6（b）所示的樣子，其角速度如圖7所示。

圖7 運行結果

本來是給世界坐標系的軸施加力矩，實際上物體卻沒有繞世界坐標系的軸旋轉而是發生了偏移，角速度為（1.02，0，-0.312）。

4.3 ForceMode

AddTorque與AddForce一樣也有ForceMode選項，包括 Acceleration，Force，Impulse，VelocityChange，含義也都與AddForce中一樣，只不過這幾個量改變的是角速度，默認Force可以省略，具體如下文給出的代碼所示：

含義是對角速度的改變量為10 rad/s，可以推知，作用時間為0.02 s時速度的改變量為0.2 rad/s，不 用考慮轉動慣量。

ForceMode.Impulse是沖量，需要考慮轉動慣量：

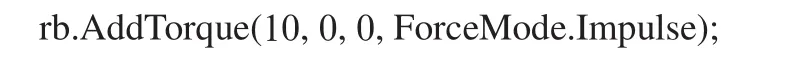
ForceMode.VelocityChange是每次直接改變角速度，不用考慮轉動慣量，代碼為：

5 結 論

動量定理是物理學中的一個基本規律。在Unity3D中，動量定理在剛體運動過程中充分體現，基于此定理的基礎上可以計算出物體的運動狀態，從而使用戶更精確地去控制虛擬物體的運動。