汽車操縱穩定性的研究

莫小琴，葉家明

（三亞學院，海南 三亞 572022）

0 引 言

20世紀以前，關于汽車的操縱穩定性，工程師很少對其進行深入的研究。20世紀30年代是汽車研究歷史上一個重要的分水嶺，其后開始對汽車操縱穩定性進行深入研究，并從中得到了許多成果，使得后來的汽車發展進步如有神助，其發展過程主要可分為四個階段：

第一階段：早于20世紀30年代。20世紀初，專家們專門研究了汽車車輪與路面接觸的懸架設計。該設計的初衷是確保行車中底盤與路面的直接接觸。使得懸架的設計符合轉向控制的需求。20世紀30年代，出現了汽車研究歷史上的一個重要分水嶺，人們對車輛控制研究的重視程度無可比擬，其中包含靜態懸架的重新解構設計，并于1925年對動力學的原理做出大膽假設。這一時期，Broulheit對輪胎角度偏轉的設定提出了自己的質疑和觀念。

第二階段：20世紀50年代之前。這一階段中，英國的Lancheste和美國的Olley開發出單獨可拆卸的車輛懸架，優化了汽車的乘坐體驗且維修成本下降，使得人們對汽車結構的認知有了新的突破。這一時期多個學者對輪胎橫向力學有了許多新的觀點，20世紀30年代后，Becker，From和Maruhn針對輪胎在轉彎過程中發生的特殊形變刊登文章，引起了多方的思考性。1934年，奧利首次提出速度作為衡量汽車的一個重要指標，并基于現有的研究成果對汽車輪胎材質的特性進行了研究。

第三階段：從20世紀50年代初期到70年代。1956年，William通過研究對汽車穩定做了進一步的研究和設計，他的研究結果為車輛的理論基礎提供了支撐，時至今日這一理論仍是汽車研究的根本。這一時期Milliken指出現有的結果仍需大量的實驗檢驗其正確性，然而當時由于實驗條件的受限人們無法做出更進一步的突破。隨后在Whitcomb的研究下，從自由度的研究出發首次引入了多自由度底盤設計的概念。

第四階段：20世紀70年代以后。自20世紀中期，隨著網絡的快速發展，在軟件中可以更好地整合操作系統安全數據。在車輛中發展“動畫”的游戲越來越復雜，也越來越現實。這一階段中，開發工程師有了人與汽車進行互通的想法和觀念，編譯代碼使得汽車上有了簡易的智能助手端，為汽車的操作提供更多可能性。

在中國，對車輛可操縱穩定性的研究直到20世紀70年代才開始。清華大學首先開始了這一領域的研究。許多生產工廠也面向產品的需求。在各個方面對車輛的穩定性進行了試驗和研究。

自1981年以來，郭孔輝教授針對汽車不相關的特性進行了深入的研究，在多種影響因素的測定下對汽車的綜合性能做出評估，作為一輛優秀的汽車，其規定綜合指標的系數值應大于0.99。20世紀90年代，郭孔輝教授發表了明確的指標，對各術語的總體方差進行了評價，并通過頻率統計分析，對閉環系統的主動安全設計進行了綜合評價和優化。

1 懸架系統動力學仿真理論

多體系統動力學是研究多體系統運動規律的一門專業學科，包括兩種動力學：剛性多體系統動力學和柔性多體系統動力學。多個系統通常由幾個靈活和剛性的對象連接在一起，在其成長階段，多方助力使得其能夠持續見漲，充分利用了生物、機械、空間等知識體系，使得其底蘊越發壯大，系統動力學有了更多地涉足領域，以下介紹幾種主要的研究方法。

1.1 牛頓-歐拉方程

當牛頓-歐拉方程用于描述單個剛體為隔振器時，由于鉸鏈厚度的增加，未知變量的數量明顯增加；由此，開發一種計算機識別剛體連接和鉸鏈的程序化方法，并自動消除鉸鏈的約束。這種方法的特點是，將非獨立的笛卡爾廣義坐標在列舉完整系統中的牛頓-歐拉方程后轉化為自變量，并通過使用有限元法消除完整系統的限制性反應原則；以及利用Jordan原理消除非完整系統的約束反作用，得到了具有相同自由度的動力學方程自由。

1.2 拉格朗日法

由于多層體系統的復雜性，用系統的拉格朗日法坐標建立系統的難度是非常大的。使用系統的一般笛卡爾坐標更合適。基于現有的二維或三維空間體系，乘子拉格朗日方程不同于原先的拉格朗日方程，引入乘子這一變量，其代表的是微分方程。導出的動力學方程給出了相同的結果。它們必須由一般的閉坐標、代數方程來完成。1973年，美國密歇根大學等多所研究機構使用集耳非柔性積分算法，對其求解效率進行了拔高，亞達算法初具模型；戴馬斯算法誕生于1977年，Edward等人基于坐標的細化提出設想，在該算法的基礎上誕生了現有的應用最為廣泛的動力學軟件——ADAMS動力學自動化軟件。

1.3 圖論（R-W）方法

在小羅伯森和比爾格的奇思妙想下，首次將建筑系的知識與動力學結合，以及用一些基礎概念和數學工具來敘述系統中剛體之間的關系。RW這種方法需要一個非常優美的正方形邊緣。多階段木質車身系統提案結構用于無木體系，應采用吊線或剛體截面將其轉換為木體系，R-W法的與眾不同之處在于其以相對位移為核心變量設計整體的數學框架，運動方程迅速興起。

1.4 變分法

經典力學是對現有事物抽象的描述，原先科學技術的落后導致人們無法對較大的數據進行計算，導致存在一定的思維漏洞，但科學技術的進步使得原先不可能實現的變分法變為現實，數據計算不再是阻攔力學發展的攔路虎，這是解決動態規律的有效途徑。在工業生產中，動態分析是檢驗合格化的標準之一，控制系統的設計更為細致，由于變分法與鉸鏈的個數無關，因此它特別適用于多鎖環復合物系統。原理高斯最小極限是不同方法的基本原理。采用最優化理論，運動數據可以直接從功能端得到。在此理論研究下，微分方程被忽略不計，減少了求解所需的計算量，并且可以與最優控制理論完美相疊加。

2 多體系統動力學建模與求解過程

多體系統動力學的流程主要包含兩部分：建模設計與仿真分析，其中建模設計利用物理和數學的思維邏輯進行研究，物理模型是根據幾何模型設計模型，數學模型是在物理知識的基礎上衍生出模型。利用簡單的幾何原理即可推導出系統整體的動態特性，在動態特性研究中或從一般幾何模型中導入。物理模型元素，例如：運動限制、駕駛限制，在幾何模型中加入動力元件和外力或外力矩，形成物理模型來表達系統的力學性能。物理模型利用笛卡爾坐標系或Josephlouis-Lagrange坐標系。基于系統運動方程的系數矩陣自動生成系統數學模型；系統的數學模型應分為動力學模型和動力學模型。靜態平衡法或求解能力動態分析的逆求解對問題的結果進行逼近，再一次次逆求解，結合結果對設計目標進行對比驗證，并回饋給物理模型或幾何模型的選擇，最終得到最完美的設計結果。

2.1 基于ADAMS懸架系統建模

研究目的在于整改車輛參數標準值，不同于固有的開發過程，需要進行數以萬計的整改和測驗。利用ADAMS軟件建模是為了方便參數的整改，減少開發周期，控制成本，提高質量，得到最優的方案。動態仿真與實驗研究相結合，深入研究ADAMS動態模擬系統，結合汽車產品開發項目進行動態模擬，進行汽車動態穩定試驗。麥弗遜式懸架是獨立懸架中的一種，車輛的前橋多數用的是麥弗遜式懸架。簡單來說，麥弗遜式懸架的組成有螺旋彈簧、減振器和控制臂，減震器的作用是限制彈簧，使彈簧只能根據指令的方向運動。麥弗遜式懸架和別的懸架系統相比較有以下優點：結構簡單、緊湊、體積小，其性能指標數值達到最高，故多在前驅式的汽車上見有麥弗遜式懸架的身影。雖然麥弗遜式懸架的優點多，但也有缺點，缺點是左右沖擊缺乏阻擋力，制動阻力不足。

為確保系統的減震器增加使用壽命，中部位置的中心減振器和彈簧中心不會在同一條線上，這種結構導致麥克弗森式懸架系統和其他懸架系統的運動規律完全不同。對mcferson型單一前懸架進行系統原理驗證，在舍去不必要的外部影響因素后得到的動力學模型如圖1所示。

圖1 麥弗遜前懸架結構簡圖

通過空間坐標系內的落座點即可進行前輪的位置確定，如式（1）至（4）：

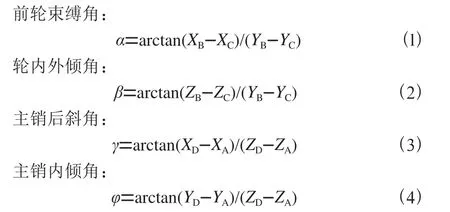
式中：A為操作臂與各個連接控制點；D為減振器與車體的鉸接點；B、C分別是輪軸內外端點。

2.2 懸架模型自由度分析

通過對設計模型進行簡化設計，懸掛系統比以往更輕，性能更好。具體如表1所示。

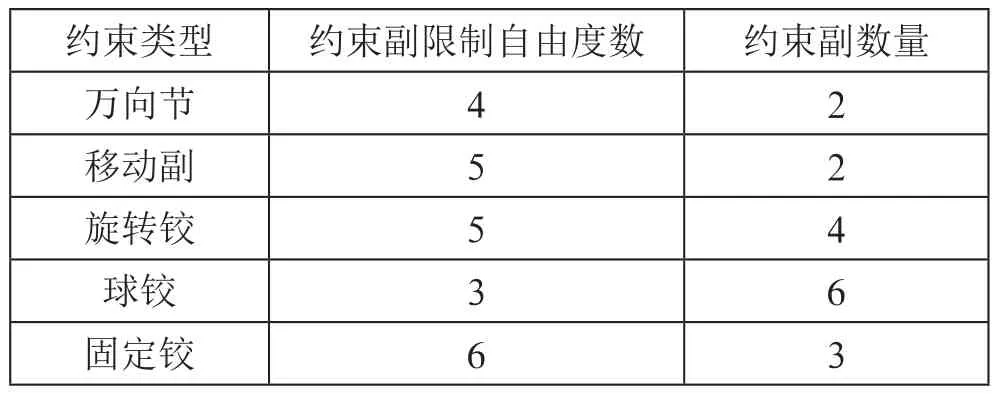
表1 前懸架各約束副類型和數目

由式（5）可得整體的自由度：

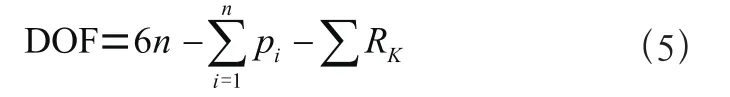
式中：為活動構件總量；p，為約束邊界及運動下限制；R為其他約束邊界。

在此基礎上獲得的整體自由度計算為：

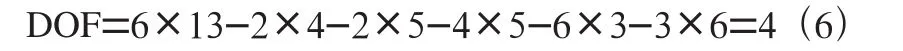
通過計算本文設計的懸掛系統的自由度為4，四個車輪和主梁可以進行轉動。

3 基于ADAMS的動力學仿真

3.1 車輪同向激振仿真

3.1.1 車輪外傾角

為了防止車輪過多轉動或旋轉，一般輪胎在50 mm的范圍內工作，外傾角的變化小于1°。當懸掛系統模型在靜力平衡時，外傾角為-0.333 3°，圖2表示的是車輪在行駛進程中轉角變化的角度分布。在本文設計的懸掛系統下，車前輪轉角的值在-1.37°～1.21°之間。在行車遇到坑洼地面的情況下，車輪前外傾角會變得更加合理。

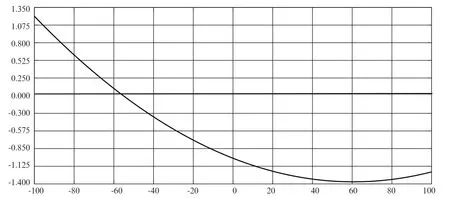
圖2 同向跳動前輪外傾角變化曲線

3.1.2 車輪前束角

在汽車運動進行時，前束角并非保持恒定不變，每次的轉換都會對來復式的運動造成影響，輪胎受到的來自地面的摩擦阻力逐漸增加，輪胎磨損程度加劇。針對這一現象，應在合理范圍內保證前束角數值的最小化。這個模型的VMS的靜力平衡時，夾角為0°。圖3中前輪前束角變化率為-4.2°至0.33°，和理想的數值存在較大程度的偏差。

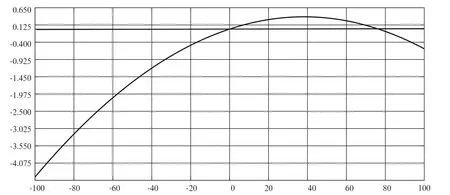
圖3 同向跳動前輪前束角變化曲線

3.2 車輪彈塑性運動仿真

3.2.1 車輪外傾角

與同步車輪受迫模擬原理類似，結合工程質量標準將實驗初始激勵保持在100 mm。運動學分析模式切換到時尚，符合更換軸箱的剛性約束機制、橡皮筋和所有其他條件和參

圖4顯示了外部傾角作為車輪均勻運動函數的變化規律曲線。根據輸出模擬結果，可以看出，傾角的變化范圍為-124°～120°，在車輪運動時，外傾角的變化略高于期望值。數保持不變，車輪定位參數的分析及其他特點，暫停了后輪的視運動期間，向上和向下移動懸架系統。

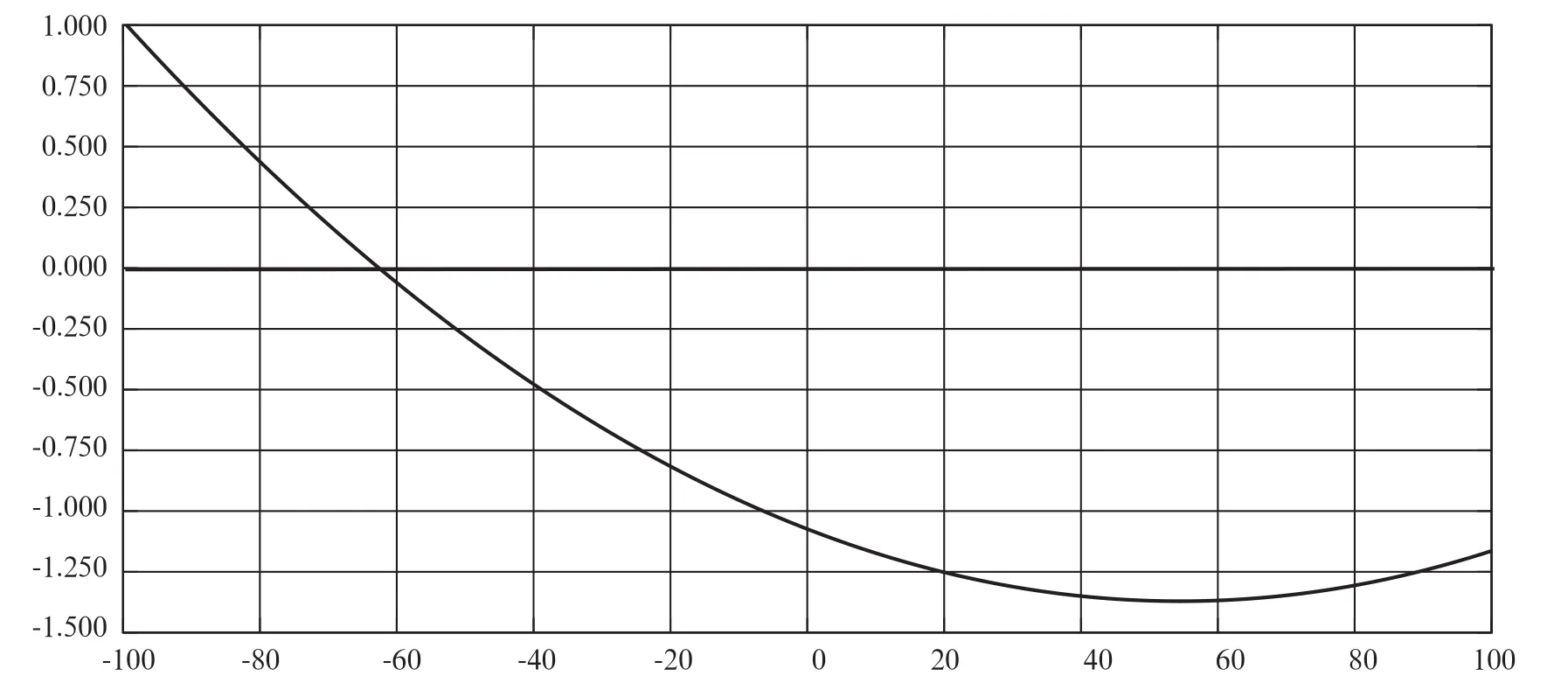
圖4 同向跳動前輪外傾角變化曲線

3.2.2 車輪前束角

圖5為前輪前梁角度作為車輪位移函數的曲線。前束的角度在4.15和0.62之間變化。當車輪運動時，前照角度的參數值變化區間高于理論的參數值。

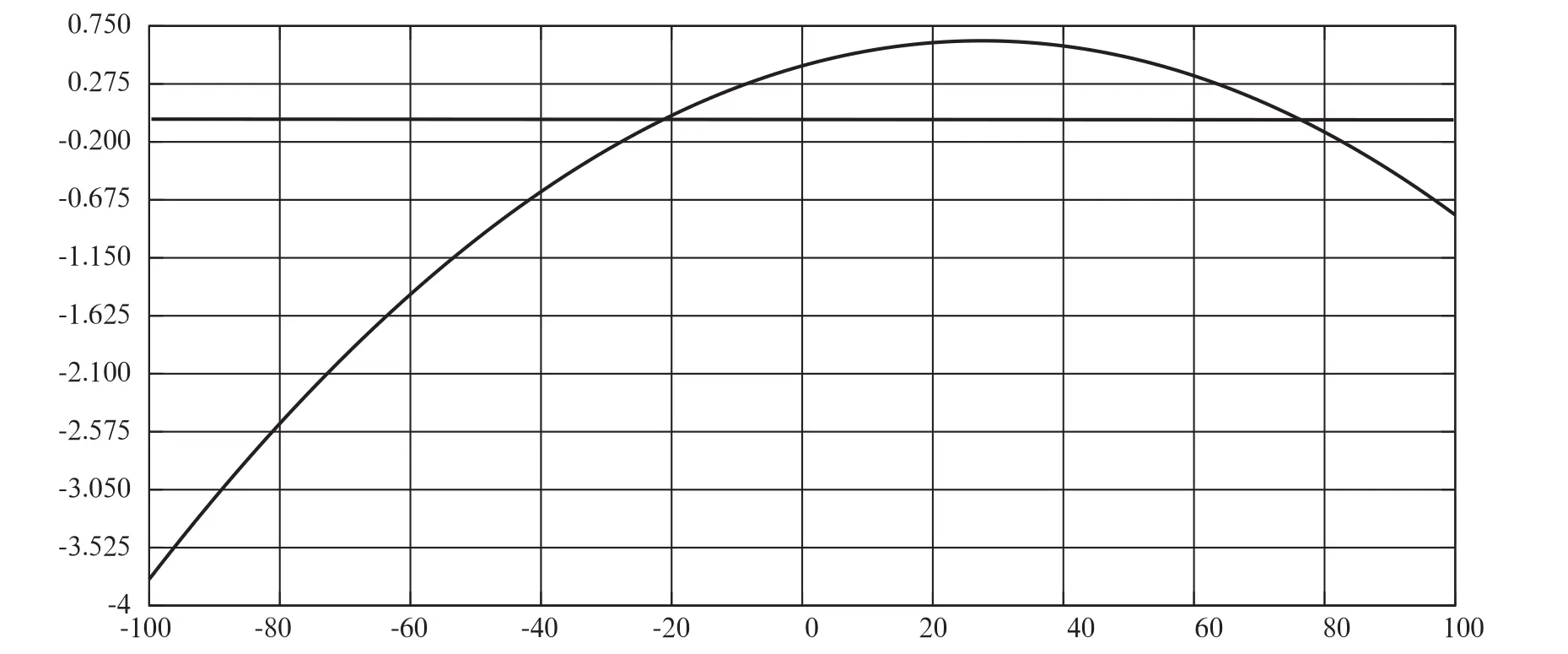
圖5 同向跳動前輪前束角變化曲線

4 結 論

根據ADAMS-虛擬樣品技術，對Macpherson型前獨立懸吊系統的性能指標進行衡量，使得汽車開發周期縮短的同時更能保證產品效果，實現雙重的便捷性。使用ADAMS設計和分析了前獨立的麥弗遜虛擬掛車的懸掛結構。對設計的汽車懸架結構進行了軟件的仿真和模擬，并在不同條件下進行了相應的測試。仿真表明，在彈性塑性限制下，主銷內傾角、車輪束前角大于固體運動時的傾角。