超高場脈沖磁體失效及結構屈曲研究

肖后秀 黃 煜

超高場脈沖磁體失效及結構屈曲研究

肖后秀1,2黃 煜1,2

（1. 華中科技大學國家脈沖強磁場科學中心 武漢 430074 2. 華中科技大學電氣與電子工程學院 武漢 430074）

結構力學表明，磁體失效包含材料強度失效和結構整體失效兩個方面。現有磁體失效模型是基于材料強度模型，忽略結構失穩問題，難以解釋超高場脈沖磁體經常在低于其設計值就發生破壞的現象。且已有研究顯示，屈曲是導致超高場脈沖磁體失效的主要原因之一，但脈沖磁體屈曲的形成機理和演變規律尚不明確。該文從結構穩定性的角度出發，分析指出脈沖磁體自由分離層可等效為薄壁圓柱殼，具有高屈曲風險，并提出基于圓柱殼體結構屈曲的超高場脈沖磁體力學失效分析方法，建立脈沖磁體靜態電磁屈曲Ansys有限元模型，進行了屈曲行為研究分析，仿真結果與實際結果吻合。屈曲分析結果表明：在電磁載荷方面，軸向電磁力是產生屈曲的決定性因素，徑向電磁力對于外層繞組軸向屈曲的影響不明顯，可在一定程度上抑制內層繞組的軸向屈曲；在繞組結構方面，外層繞組對螺旋繞組縫隙較為敏感，需重點關注。

脈沖強磁場 脈沖磁體 自由分離層 屈曲

0 引言

強磁場對核磁矩、電子自旋和電子軌道磁矩都有強烈作用，是現代基礎科學研究最為重要的極端條件之一，相關研究產生了整數量子霍爾效應、分數量子霍爾效應等十余項諾貝爾獎[1]。磁場強度越高，對物質作用的效果越明顯，發現新現象和新原理的可能性也越大，會催生更多重大成果。為促進基礎科學的發展，我國已經建成了脈沖強磁場國家重大科技基礎設施。

脈沖強磁場技術是目前產生50T以上非破壞性強磁場的最有效技術途徑，而脈沖磁體是其中關鍵核心技術。脈沖磁體結構及受力方向如圖1a所示，脈沖磁體由多層特殊加固的空心螺線管組成，工作在瞬變超高磁場、大電流、高電壓等條件下，承受著巨大的電磁力，如100T時達到4GPa（最強合金金屬強度的2倍）[1-2]。強大電磁力下脈沖磁體壽命短、易失效，其中力學破壞是脈沖磁體的首要矛盾，力學失效機制研究是重中之重，對于提升脈沖磁體技術水平十分關鍵[3]。同時，脈沖磁體也是一種典型的極端電磁能裝置，其力學失效機制的精準闡釋對發展線圈炮、電磁軌道炮等極端電磁能裝備也有潛在的借鑒意義。

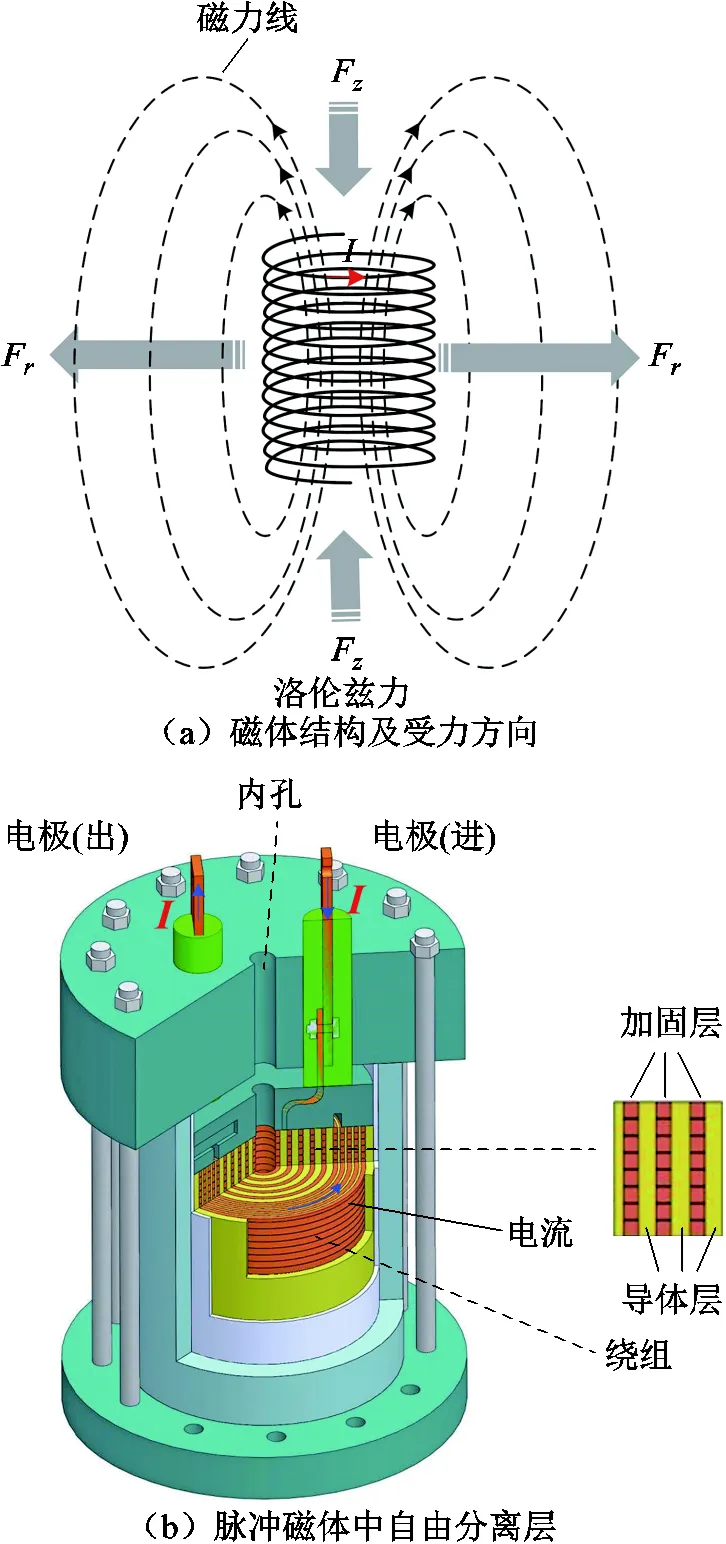
脈沖磁體的失效分析建立在力學模型基礎之上，脈沖磁體力學理論主要經歷了三個發展階段：一維彈性模型[4-5]、一維彈塑性模型[4,6]以及二維軸對稱彈塑性模型[7]。脈沖磁體的結構和電磁特性具有上下和軸對稱性，早期研究對軸向電磁力F做了簡化等效，重點研究徑向電磁力F的作用，建立磁體中平面的一維彈性力學模型，隨后發展出了一維彈塑性力學模型，脈沖磁體中自由分離層如圖1b所示。一維模型的提出有力推動了磁體失效機制研究和磁體技術發展。研究人員據此發現了應力向內層集中的磁體失效機理[4,8]，并發展了自由分離和分層加固技術[1,9-10]，磁場強度從40T提升至70T以上[1,9]。

隨著磁場強度提高到70T以上，軸向壓縮變形不可忽略，一維模型中軸向電磁力F的簡化等效會造成較大誤差，已不再適用。考慮了軸向變形的二維軸對稱模型（見圖1c）逐漸成為主流，并取得豐碩研究成果：德國S. Zherlitsyn指出層間過渡處繞組的明顯軸向移動可能會觸發磁體失效[11]；美國D. N. Nguyen[12]指出冷卻通道造成的應力集中會縮短磁體壽命；法國P. Frings[13]發現了磁體中導體累計塑性軟化效應會影響磁體壽命。

2010年以來，世界各國都在不斷追求100T極限磁場，但成少敗多，基于經典理論設計的高場磁體常常顯著低于理論值就發生破壞，而且無法合理解釋失效機制，其存在的缺陷和不足愈發突出。例如，國家脈沖強磁場科學中心（WHMFC）于2017～ 2021年間多次沖擊100T，但磁體都在低應力水平下發生破壞（2.5GPa, 83T），遠低于設計限值（4GPa）。美國國家強磁場實驗室（NHMFL）[14]、德國強磁場實驗室（HLD）[15]等世界頂尖脈沖強磁場實驗室的100T磁體也是如此，美國的100T超高場脈沖磁體更是失敗了8次之多。

超高場磁體理論設計嚴重偏差現象已成為當前脈沖磁體技術發展中的難題。究其原因，現有磁體失效模型都是在彈塑性小變形假設下計算應力分布，然后通過von Mises或其他等效應力進行強度判斷，從本質上看都屬于材料強度模型[16]。該模型在以往80T以下脈沖磁體分析設計中得到了驗證，理論計算結果與實驗結果吻合較好，這主要歸因于該類磁體體積和所受到的電磁力都相對較小，結構失穩風險低，材料強度破壞是磁體失效的主因。但是，依據結構力學理論可知，隨著磁場強度的提高和磁體結構的增大，脈沖磁體中主要力學矛盾從局部的材料強度問題逐漸轉化為全局的結構穩定性問題，特別是具有薄壁特征自由分離層的失穩，而相關理論研究尚在起步階段。

綜上所述，超高場脈沖磁體在材料強度破壞之前可能發生薄壁繞組層整體結構失穩，現有強度失效模型無法準確描述，亟需開展結構失穩理論和方法等方面的研究。本文將從結構穩定性角度出發，分析超高場、大電流、高機械應力等極端條件下脈沖磁體自由分離層所形成薄壁結構的電磁屈曲行為。

1 圓柱殼結構屈曲的基本概念

如圖1a，脈沖磁體由多層特殊加固的空心螺線管組成，承受著“徑向膨脹、軸向壓縮”的電磁力。為抵抗強大的電磁力，每層繞組外都有高強度纖維加固層，同時通過設置多個自由分離層避免應力集中，在徑向電磁作用下自由分離層會形成薄壁層（如圖1b中前五層，此圖為1/2軸對稱模型）。

依據結構力學屈曲理論可知，脈沖磁體中自由分離層具有薄壁特征，在軸向電磁壓力下，易發生軸向屈曲變形。自由分離層可等效為圓柱殼體，其屈曲變形行為屬于圓柱殼體屈曲范疇，本文將圍繞結構力學中圓柱殼體展開闡述。依據載荷類型，可分為靜態和動態屈曲分析兩類；依據材料特性，又可分為線性和非線性屈曲兩類，其中線性屈曲相對簡單，已經有成熟解析模型。

軸向壓力下的薄壁圓柱殼模型如圖2所示。圖2中，為殼體平均半徑，為厚度，為長度。依據線性屈曲理論可得到對應屈曲軸向壓應力（也稱為屈曲強度）為[17-18]

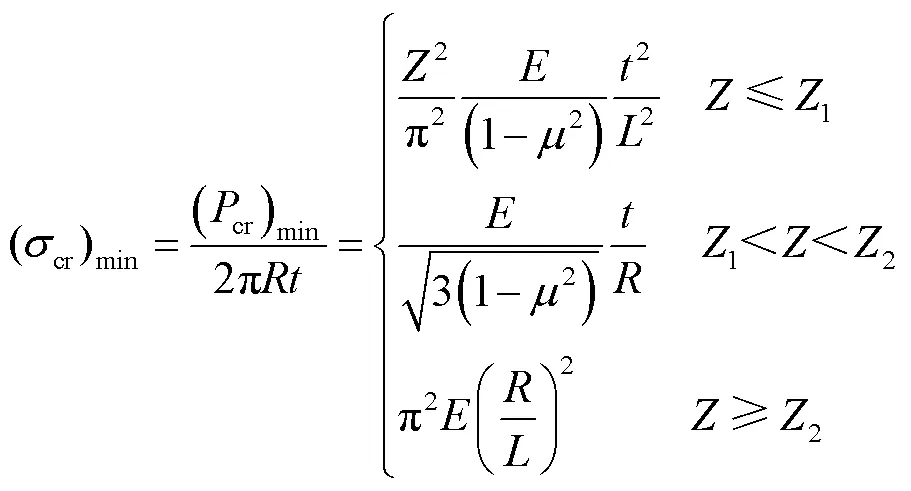
式中，為楊氏模量；為Batdorf參數[17]，取決于圓柱殼的幾何參數和材料屬性（泊松比），其表達式為

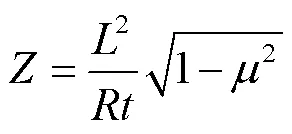
為研究幾何尺寸對屈曲行為的影響，對多種實際磁體尺寸的金屬結構圓柱殼（銅筒）進行解析解和有限元分析，如圖3所示。圓柱殼高度為100～500mm，圓柱殼半徑為10～100mm，圓柱殼厚度為2～10mm，對應的Batdorf參數范圍在10～11 800。圖3中和為屈曲模數，反映了屈曲的變形特征。

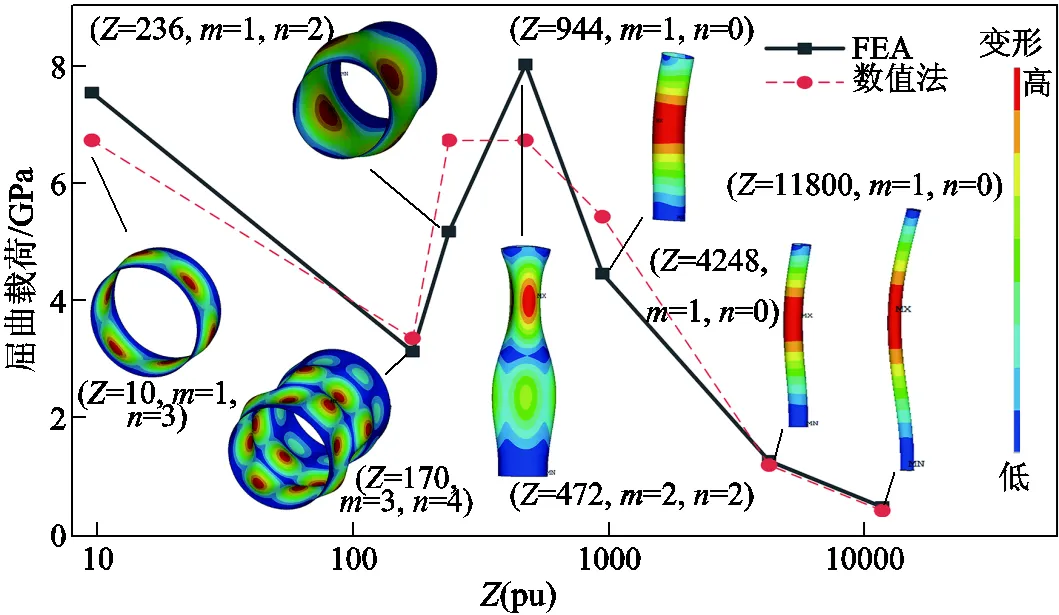
圖3 不同幾何結構圓柱殼的屈曲行為

可以得到以下結論：①隨著參數的增加，屈曲模式逐漸從短筒向中筒、長筒特征轉變，軸向徑向屈曲模數先增大后減少，最后表現為歐拉屈曲模式（細長桿,=1,=1）；②與此對應的屈曲載荷，也呈現先降低，后增加，再減少的趨勢；③任何類型圓柱殼屈曲時的都大于0，而是可以等于0的（以短型圓柱殼為主）。需要指出的是，常規脈沖磁體的Batdorf參數一般在100以上，對應圖3中的右半部分，即脈沖磁體中不會存在短型圓柱殼情況，主要以中長型圓柱殼為主。磁體的最內層自由分離繞組屬于細長筒結構，而中部自由分離層屬于中長筒。單從結構上看，長筒屈曲載荷將比中筒屈曲載荷低一些，即磁體的內層比中層對軸向載荷更敏感。但實際中，還需要考慮電磁力的分布情況，會造成不同結果。

2 分布電磁力下的脈沖磁體屈曲分析

圓柱殼在集中載荷作用下的線性屈曲分析可以在一定程度上反映脈沖磁體的結構特點，但與實際中脈沖磁體屈曲行為還有很大差距：①脈沖磁體中是體分布的電磁載荷，這會使得脈沖磁體的屈曲行為有很大不同；②同時脈沖磁體導體進入了深度塑性階段，也需要考慮材料非線性；③最后徑向外壓對脈沖磁體屈曲行為的影響也不可忽視。因此，分析相關問題的難點在于：在超高場條件下，線性屈曲理論關于軸向集中載荷、材料小變形（處于彈性階段）的假設已經失效，磁體的屈曲臨界載荷不能通過經典解析公式獲得，需要綜合考慮電磁-結構多場耦合、電磁力分布、材料非線性、幾何大變形等因素的影響。

本文利用Ansys有限元軟件進行電磁場-結構場多場耦合分析，基于節點法求解電磁場，建立考慮了材料非線性、幾何大變形的非線性屈曲有限元模型。流程如圖4所示，包括有限元建模、電磁場分析、預應力分析、線性/非線性屈曲等四個步驟。為分析繞組中電磁力載荷，需要先使用SOLID97單元求解單繞組層產生的磁場和電磁載荷，然后，刪除空氣單元，完善材料屬性，進入力學求解環節。采用SOLID185單元和Lanczos法分別先進行預應力求解和線性屈曲求解，接著將線性屈曲的模態作為初始微擾（通常取0.1%）并打開大變形開關，采用弧長法進行非線性屈曲求解。超高場工況下脈沖磁體中導體材料處于塑性、非線性狀態，非線性屈曲方法可以更為準確地計算脈沖磁體屈曲行為。

圖4 Ansys模型分析過程

下面將仿照實際80T脈沖磁體內線圈的最內層和最外層繞組參數，進行單層繞組的電磁屈曲行為分析。兩層磁體繞組具體參數見表1。兩層繞組均為40匝，銅導線為2.4mm×4.4mm，加固纖維為1mm厚的柴龍纖維（Zylon），8kA電流驅動下分別在中心產生2.33T和2.15T磁場，它們分別屬于長型圓柱殼和中型圓柱殼。在進行電磁分析后，其中中長筒電磁場和電磁力分布結果如圖5所示。

表1 兩層繞組主要參數

Tab.1 Main parameters of two winding layers

在非線性屈曲求解過程中，兩個繞組的軸向縮短位移-載荷曲線如圖6所示。對于給定結構的線圈，電磁力載荷與磁感應強度密切相關（∝2），采用磁場標定線圈載荷使得磁體分析設計更為方便，將以磁感應強度代表電磁力載荷。當磁場隨軸向縮短量的增長斜率為0時，這表明已經達到了結構所能承受的最大載荷，即為屈曲點。內外層繞組對應的屈曲磁場分別為19.67T和7.2T，內層繞組屈曲磁場高于外層，主要由于內層線圈內部磁場較為均勻，徑向磁場（軸向電磁力）分量較低，而外層繞組則反之，所以內層繞組屈曲磁場較高。這說明軸向電磁載荷在脈沖磁體屈曲過程占主導作用。由圖6可知，基于非線性屈曲的計算結果表明內層線圈應呈現出軸向彎曲破壞，而外層線圈呈現為中部破壞。

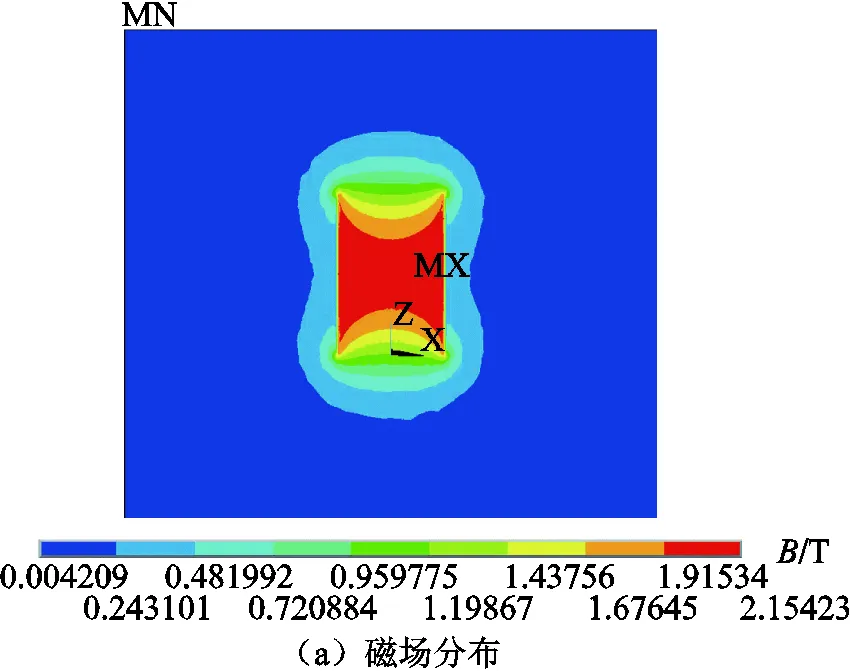
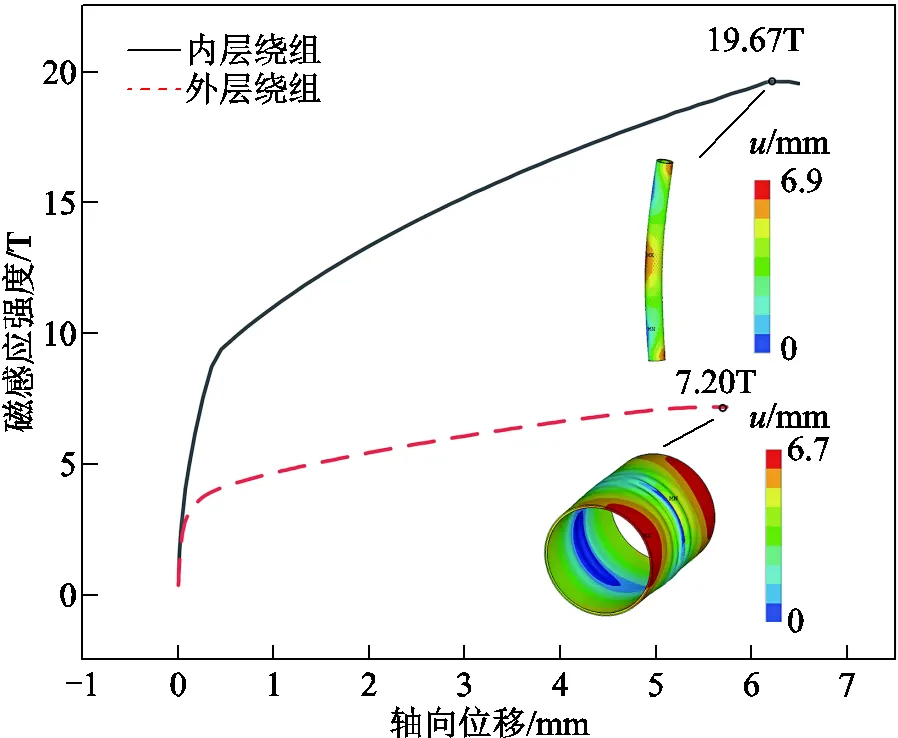
圖6 非線性屈曲求解中位移-載荷曲線

圖7a給出了基于非線性屈曲計算得到的外線圈結果，而圖7b則為美國NHMFL強磁場實驗室80 T磁體破壞前后[19]的圖片。衡量屈曲行為主要指標是屈曲破壞形式和屈曲強度。從仿真結果與實際結果對比可以看出，二者都是在磁體中部發生破壞，而且均有明顯的軸向彎曲。實際磁體的破壞形式和破壞時磁場與經典材料強度破壞不同，而與屈曲模型理論預測接近，表明了本文所采取的研究方法和建立模型的正確性。

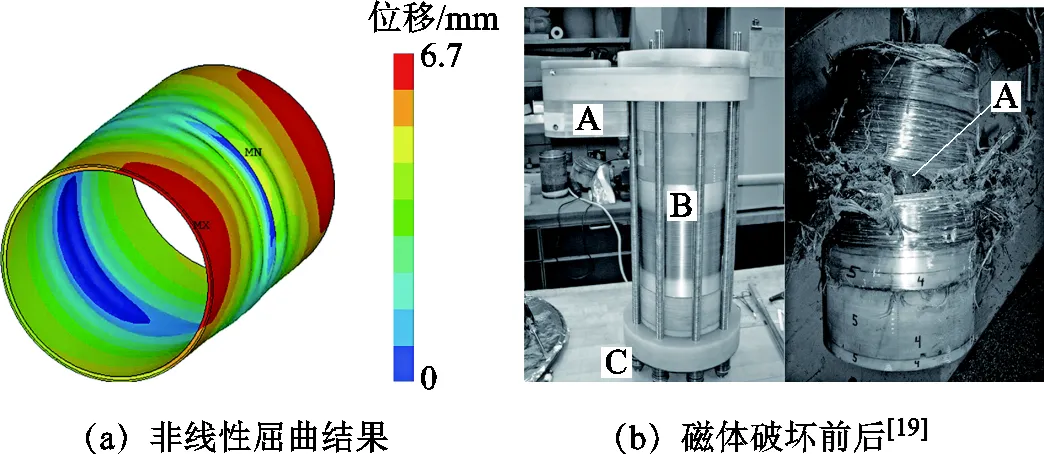
圖7 中長型繞組屈曲仿真和實驗結果對比

徑向電磁力對軸向屈曲行為的影響如圖8所示，橫坐標F(,) /F0(,)表示徑向電磁載荷的放大倍數，縱坐標/0為其相應屈曲磁場與1倍徑向電磁載荷的比值。對于內層繞組，其屈曲磁場強度隨著徑向電磁載荷的增大先上升后減小，在這變化的過程中經歷了屈曲的轉變，從歐拉桿狀屈曲（=1,=1）變成了盤狀屈曲（=1,=0）。而且，徑向電磁載荷的存在一定程度上提高了其軸向穩定性。而外層繞組的屈曲磁場隨著徑向電磁載荷比例的增大而出現了小幅度降低，影響不顯著。

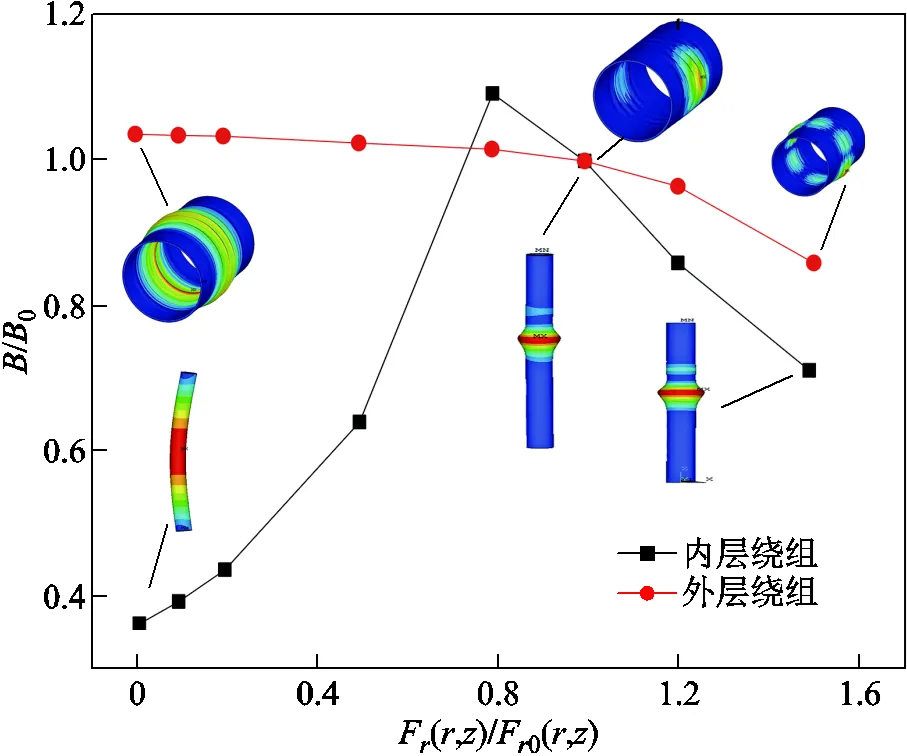
圖8 徑向電磁力對軸向屈曲強度的影響

實際中磁體導體層并不是一個完整的圓柱殼，是由螺旋繞組與加固層組成的，可等效為加筋圓柱殼，只不過這個“筋”占比較大，需要研究螺旋繞組縫隙對屈曲強度和模態的影響。在電磁載荷下，內層和外層繞組中導線占空比對屈曲強度的影響如圖9所示，導線所占比例從50%到100%，屈曲強度歸一化值相應從0.45提高到了1，表明螺旋繞組縫隙對屈曲強度有很大影響，縫隙越大，屈曲強度越低。在占空比較大時，外層圓柱殼結構比長型線圈更為敏感，當縫隙寬度超過一定限度時，結構穩定性都將出現大幅下降。而實際中脈沖磁體是密繞螺線管，導線占空比往往很大（80%以上），縫隙極小，縫隙影響是有限的。

圖9 螺旋繞組對屈曲強度的影響

3 結論

結構力學表明，磁體失效包含材料強度失效和結構整體失效兩個方面。然而，現有磁體失效模型是基于材料強度模型，忽略了結構失穩問題，難以解釋超高場脈沖磁體經常低于其設計值就發生破壞的現象。因此，本文從結構穩定性的角度出發，重點研究脈沖磁體自由分離的薄壁層，提出了基于圓柱殼體結構屈曲的超高場脈沖磁體力學失效分析方法，建立并計算了脈沖磁體靜態電磁屈曲Ansys有限元模型，仿真結果與實際結果吻合，表明本文方法的可靠性。通過仿真對比，可以得出以下結論：

1）與經典材料強度模型相比，考慮磁體整體結構屈曲的方法可以更為準確地模擬與預測超高場脈沖磁體的力學失效行為。

2）軸向電磁載荷在脈沖磁體屈曲過程占主導作用。徑向電磁力的對于外層繞組軸向屈曲影響不明顯，但對內層繞組的軸向穩定有一定幫助。

3）在繞組結構方面，外層繞組對螺旋繞組縫隙較為敏感，需重點關注。

目前，本文的相關研究聚焦于磁體中單層繞組在磁場峰值處的靜態屈曲行為，下一步將開展動態載荷對于磁體屈曲行為的研究。

[1] Herlach F. High magnetic fields: science and technology - volume 2: theory and experiments I[M]. Singapore: World Scientific Publishing, 2006.

[2] Peng T, Jiang F, Sun Q Q, et al. Concept design of 100-T pulsed magnet at the Wuhan national high magnetic field center[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1-4.

[3] Boebinger G. High magnetic field science and technology[R]. 25th International Conference on Magnet Technology (MT25), Amsterdam, Netherlands, 2017.

[4] 王秋良. 高磁場超導磁體科學[M]. 北京: 科學出版社, 2008.

[5] Arp V. Stresses in superconducting solenoids[J]. Journal of Applied Physics, 1977, 48(5): 2026-2036.

[6] Eyssa Y M, Denis Markiewicz W, Pernambuco-Wise P. Plastic stress analysis of pulse and resistive magnets[J]. IEEE Transactions on Magnetics, 1996, 32(4): 2526-2529.

[7] Peng T, Gu C L, Rosseel K, et al. Advanced numerical simulation of pulsed magnets with a finite element method[J]. Measurement Science and Technology, 2005, 16(2): 562-568.

[8] Witters J, Herlach F. Analytical stress calculations for magnetic field coils with anisotropic modulus of elasticity[J]. Journal of Physics D: Applied Physics, 1983, 16(3): 255-260.

[9] Van Bockstal L, Heremans G, Herlach F. Coils with fibre composite reinforcement for pulsed magnetic fields in the 50-70 T range[J]. Measurement Science and Technology, 1991, 2(12): 1159-1164.

[10] Li H, Herlach F. Deformation analysis of pulsed magnets with internal and external reinforcement[J]. Measurement Science and Technology, 1995, 6(7): 1035-1042.

[11] Zherlitsyn S, Wustmann B, Herrmannsdorfer T, et al. Status of the pulsed-magnet-development program at the Dresden high magnetic field laboratory[J]. IEEE Transactions on Applied Superconductivity, 2012, 22(3): 4300603.

[12] Nguyen D N, Michel J, Mielke C H. Status and development of pulsed magnets at the NHMFL pulsed field facility[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1-5.

[13] Frings P, Billette J, Beard J, et al. New developments at the national pulsed field laboratory in Toulouse[J]. IEEE Transactions on Applied Superconductivity, 2008, 18(2): 592-595.

[14] Mielke C. The NHMFL pulsed field facility at los alamos national lab[C]//Workshop on Frontier Science Research of Pulsed High Magnetic Field, Wuhan, China, 2010: 1-26.

[15] Zherlitsyn S. Pulsed-magnet developments at the Dresden high magnetic field laboratory[C]//26th International Conference on Magnet Technology (MT26), Vancouver, Canada, 2019: 1-5.

[16] 卓衛東. 應用彈塑性力學[M]. 北京: 科學出版社, 2005.

[17] Ziemian R D. Guide to stability design criteria for metal structures[M]. 6th ed. Hoboken, NJ: John Wiley & Sons, 2010

[18] ?zgen C. Buckling analysis of circular cylinder shells under axial compression loading[D]. Istanbul: Istanbul Technical University, 2017.

[19] Swenson C A, Rickel D G, Sims J R. 80 T magnet operational performance and design implications[J]. IEEE Transactions on Applied Superconductivity, 2008, 18(2): 604-607.

Study on Failure and Structural Buckling of Ultra-High Field Pulsed Magnets

Xiao Houxiu1,2Huang Yu1,2

（1. Wuhan National High Magnetic Field Center Huazhong University of Science and Technology Wuhan 430074 China 2. School of Electrical and Electronic Engineering Huazhong University of Science and Technology Wuhan 430074 China）

The theory of structural mechanics shows that magnet failure can be attributed to over-stress failure or windings buckling. The present magnet failure model is based on the stress model and ignores the problem of structural instability, which makes it impossible to explain why ultra-high fieldmagnets frequently sustain damage at low stress levels. However, the mechanism and criterion of buckling in pulsed magnets are still unclear. Previous study has indicated that buckling is another significant cause of ultra-high field pulsed magnet failure. In this paper, the free-standing layer of the pulsed magnet can be equivalent to a thin-walled cylindrical shell with a high risk of buckling. A failure analysis method of ultra-high-field pulsed magnets based on the buckling of the cylindrical shell structure, along with an Ansys finite element model of the static electromagnetic buckling, is proposed. The simulation results match well with the experimental results. The buckling analysis shows that: the axial electromagnetic force is the key factor for buckling, while the radial electromagnetic force has no significant effect on the axial buckling of the outer winding, and itcan suppress the axial buckling of the inner winding to some extent; in terms of winding structure, the outer winding is more sensitive to the spiral winding gap and needs to be focused on.

High magnetic field, pulsed magnets, free-standing layers, buckling

10.19595/j.cnki.1000-6753.tces.211714

TM551; O342

國家重點研發計劃（2021YFA1600303）和湖北省重點研發計劃（2021BAA167）資助項目。

2021-10-26

2022-04-12

肖后秀 男，1981年生，副教授，研究方向為脈沖強磁場技術及其應用。E-mail：xiaohouxiu@mail.hust.edu.cn（通信作者）

黃 煜 男，1999年生，碩士研究生，研究方向大功率脈沖磁體回旋管及其應用。E-mail：m202172077@hust.edu.cn

（編輯 郭麗軍）