基于積木式傳遞矩陣法雙轉子系統(tǒng)臨界轉速計算

都昌兵，邱清竣，舒 毅

（長沙航空職業(yè)技術學院，湖南 長沙 410124）

帶軸間軸承的雙轉子系統(tǒng)是航空發(fā)動機的典型結構。航空發(fā)動機的使用經(jīng)驗表明：在某些轉速下，轉子的撓度顯著增大，同時出現(xiàn)較大的不平衡力和力矩，這些轉速稱為臨界轉速。如果發(fā)動機在臨界轉速附近工作，其振動大大加劇。轉子在遠小于或大于臨界轉速下運轉時，其工作平穩(wěn)，撓度很小[1]。臨界轉速現(xiàn)象是轉子系統(tǒng)的固有特性。對于單轉子系統(tǒng)來說，臨界轉速的數(shù)值由系統(tǒng)結構決定，而與工作轉速無關。但是，對于雙轉子系統(tǒng)來說，在不同轉速比下，由于軸間軸承的影響，系統(tǒng)特性（轉子相互作用、耦合作用的強弱不同）有所改變，將對臨界轉速產生影響。

1 積木式傳遞矩陣的基本原理

積木式傳遞矩陣是一種用于計算單、雙轉子系統(tǒng)臨界轉速的理想方法。任何復雜的轉子均可由若干“標準”類型的轉子大段（簡稱：積木塊）組合而成，積木塊的右端為轉子始端或軸承結合面的左側，其左端為轉子的末端或軸承結合面的右側。對每類積木塊分別編制了由其右端狀態(tài)變量來計算其左端狀態(tài)變量的標準程序。當要計算實際轉子的臨界轉速時，只要將相應的積木塊程序調用搭接即可[2]，而不需要重新編制源程序。

2 航空發(fā)動機典型構件的傳遞矩陣

2.1 帶彈性支承的剛性薄圓盤

對于帶彈性支承的剛性薄圓盤，設第j個支承的總剛度為Ksj，其傳遞矩陣為：

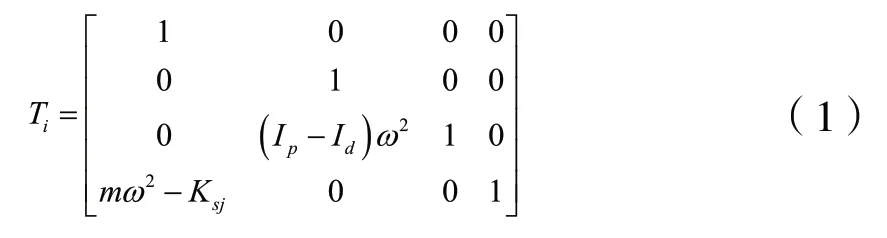
式中：Ip、Id分別為單元直徑轉動慣量、單元極轉動慣量，m為剛性圓盤集質量，ω為轉速。

2.2 無質量等截面的彈性軸段

無質量等截面的彈性軸段的傳遞矩陣為：

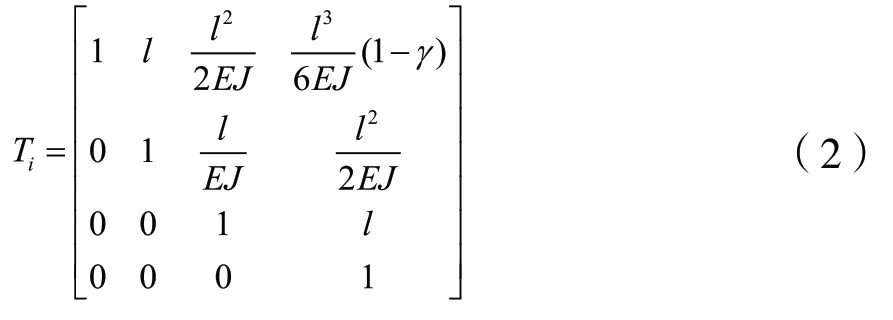
式中：l為軸段的質量，E為材料的彈性模量；J為軸段的截面距；γ為考慮剪切影響的系數(shù)。

2.3 圓盤和軸段的組合件

圓盤和軸段的組合件的傳遞矩陣為：

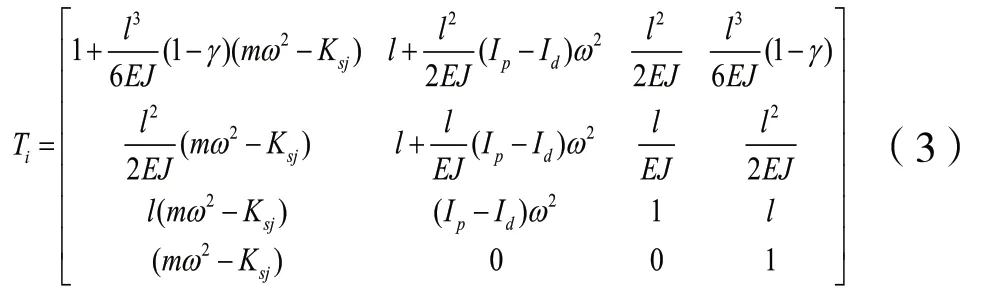
2.4 點質量

點質量的傳遞矩陣為：

3 雙轉子系統(tǒng)臨界轉速的計算

3.1 雙轉子模擬實驗器

雙轉子模擬實驗器結構如圖1所示，由內、外兩個轉子組成，其中：內轉子支承形式為1-2-1，外轉子支承形式為1-0-1，外轉子的后端采用了軸間軸承。

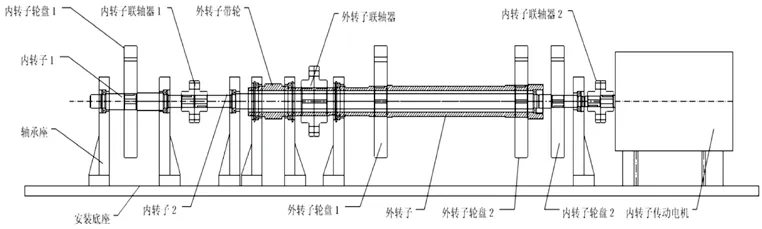
圖1 雙轉子模擬實驗器結構圖

3.2 計算模型的建立

根據(jù)雙轉子模擬實驗器的幾何、物理參數(shù)來建立轉子的傳遞矩陣理論計算模型。

（1）轉子系統(tǒng)的分段

根據(jù)支承、聯(lián)軸器的位置，把內、外轉子分為幾個大段；在各大段內根據(jù)軸的特點分站。為了便于計算，內、外轉子統(tǒng)一分段，即內、外轉子的分段數(shù)相同，相對應段的截面數(shù)也相同。由于外轉子比內轉子短，故在外轉子兩端添加質量、長度為零的虛擬段，使其和內轉子段數(shù)相同。其中KB表示內轉子的大段號，KA表示外轉子的大段號。分段的結果如圖2所示。

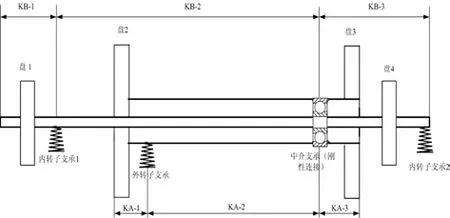
圖2 雙轉子系統(tǒng)簡化模型

內轉子之間通過柔性聯(lián)軸器連接，為了便于計算，從聯(lián)軸器處把內轉子分成兩部分。建立模型時，選取右側的軸段。

（2）軸的處理

根據(jù)軸徑以及軸上安裝零件的不同，將軸分成若干等截面的軸段，段數(shù)分得越多，計算結果越準確，但計算量也越大。凡是輪盤、軸承位置、軸徑（外徑或內徑）和材料有變化的位置，都選作分段截面。對于等截面的軸段過長的段，則將其分成若干小段。

軸的質量按集中質量處理。軸的質量簡化成有限個集中質量，各軸段的質量按質心位置不變的原則分配在各軸段的兩端面上。

（3）輪盤的處理

輪盤簡化為集中質量（位于輪盤重心截面的軸線上），但考慮其直徑轉動慣量和極轉動慣量[3]。

（4）支承條件的簡化

將支承系統(tǒng)簡化為彈性支座。支承系統(tǒng)的剛度，根據(jù)試驗或計算確定。支承的剛性系數(shù)按以下的經(jīng)驗公式計算：

①同時受徑向和軸向載荷的滾珠軸承的柔性系數(shù)[4]：

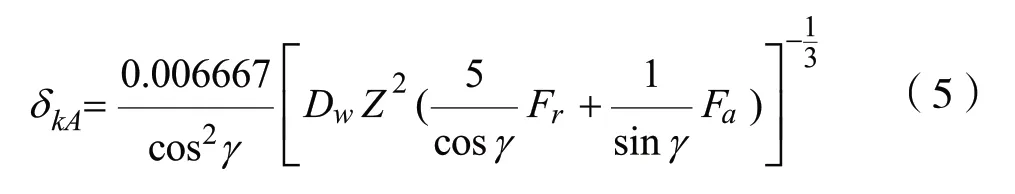
②只受徑向載荷的滾珠軸承的柔性系數(shù)：

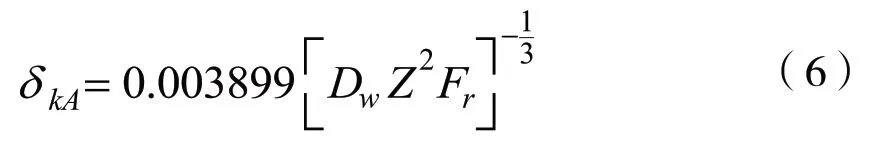
式中：

γ-滾珠與軸承外環(huán)的接觸角；Dw-滾珠直徑；

Fγ-徑向載荷；Fa-軸向載荷；Z-滾珠數(shù)量。

本文中的支承均按照彈性支承來進行處理。

（5）計算模型

按照軸分段的結果，再把每段軸分為若干個節(jié)點，經(jīng)過簡化的計算模型如圖3所示。

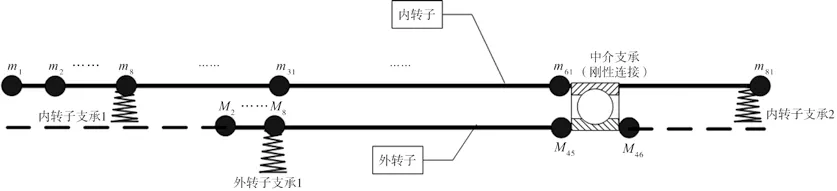
圖3 雙轉子系統(tǒng)計算模型

（6）編制數(shù)據(jù)文件

根據(jù)理論計算模型，編制數(shù)據(jù)文件。

數(shù)據(jù)文件的格式是一個18×N階的輸入矩陣。N指的是軸劃分的截面數(shù)。矩陣的各行元素為該截面的內外轉子的幾何、物理特性，如軸的長度，軸段的內徑和外徑，軸的支承條件，有無盤、聯(lián)軸器等附件，有無附加的質量等，作為選取計算模塊的依據(jù)，以及計算參數(shù)數(shù)值[5]。

3.3 邊界條件

雙轉子模擬實驗器中，外轉子的一端為懸臂端，另一端通過柔性聯(lián)軸器、傳動帶與電機相連，在理論計算模型中按自由端來處理。內轉子的一端通過柔性聯(lián)軸器與電機相連，另一端為外伸的自由端，計算時按兩端都是自由端處理。

3.4 程序流程圖

在計算內轉子臨界轉速時，先將外轉子固定在某一個轉速下，然后用頻率掃描法計算內轉子的臨界轉速。改變外轉子的轉速，重新計算在新的外轉子轉速影響下的內轉子的臨界轉速。這樣就可以得出在不同的外轉子轉速之下的內轉子的臨界轉速。計算的程序流程圖如圖4所示。

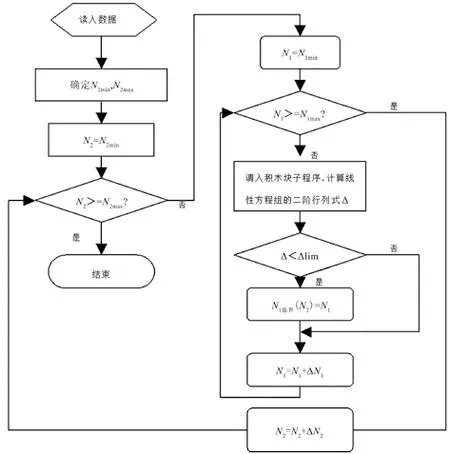
圖4 臨界轉速計算流程圖

外轉子的臨界轉速計算方法與內轉子的臨界轉速計算方法相同，即計算在不同的內轉子轉速影響之下的外轉子的臨界轉速。它的程序流程圖不再給出。

4.計算結果與分析

4.1 內轉子的臨界轉速計算結果

先給定外轉子的一個轉速，求解在該轉速下內轉子的臨界轉速值；再改變外轉子的轉速值，計算外轉子在另一個轉速下時內轉子的臨界轉速值；重復以上的計算，即可求得外轉子在各個轉速時內轉子的臨界轉速值；根據(jù)計算結果，繪制出內轉子的臨界轉速隨外轉子轉速變化的曲線，進而分析其變化規(guī)律。

（1）內轉子的一階臨界轉速隨外轉子轉速的變化

表1給出了在不同的外轉子轉速下的內轉子的一階臨界轉速的計算值。

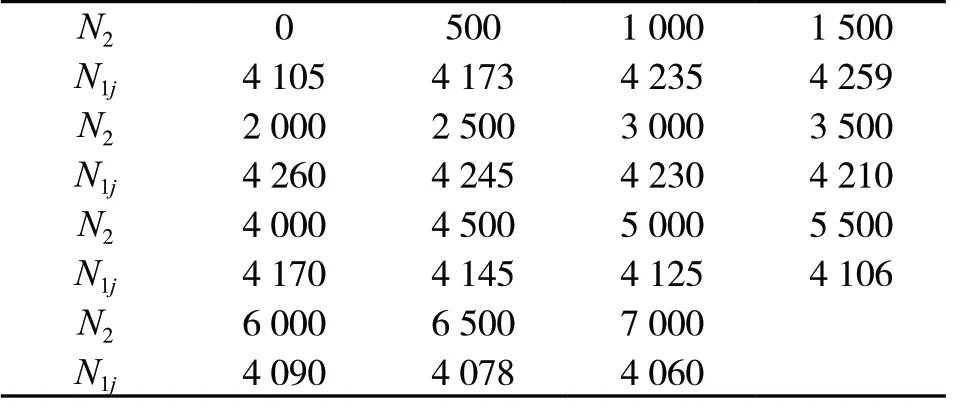
表1 內轉子的一階臨界轉速（單位：r/min）

內轉子一階臨界轉速隨外轉子轉速的變化規(guī)律如圖5所示。

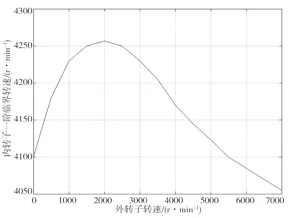
圖5 內轉子一階臨界轉速隨外轉子轉速的變化

從表1、圖5可以看出：當外轉子的轉速在0～7 000 r/min變化時，隨著外轉子轉速的增加，內轉子的一階臨界轉速先增加、后降低；在外轉子轉速值為2 000 r/min時，內轉子的一階臨界轉速達到最大。說明：轉子系統(tǒng)運轉過程中臨界轉速是變化的，變化的原因是外轉子轉速的變化導致了內轉子在中介支承處的動剛度發(fā)生了變化。動剛度的增加導致了內轉子臨界轉速的上升，動剛度的降低會導致臨界轉速的下降。

（2）內轉子的二階臨界轉速隨外轉子轉速的變化

表2給出了在不同的外轉子轉速下的內轉子二階臨界轉速的計算值。

內轉子二階臨界轉速值的變化規(guī)律如圖6所示。

從表2、圖6可以看出，隨著外轉子轉速的上升，內轉子的二階臨界轉速值上升，并且上升的幅度逐漸減小。其原因是外轉子轉速的上升導致了內轉子支承的動剛度增加，使得內轉子的二階臨界轉速上升。

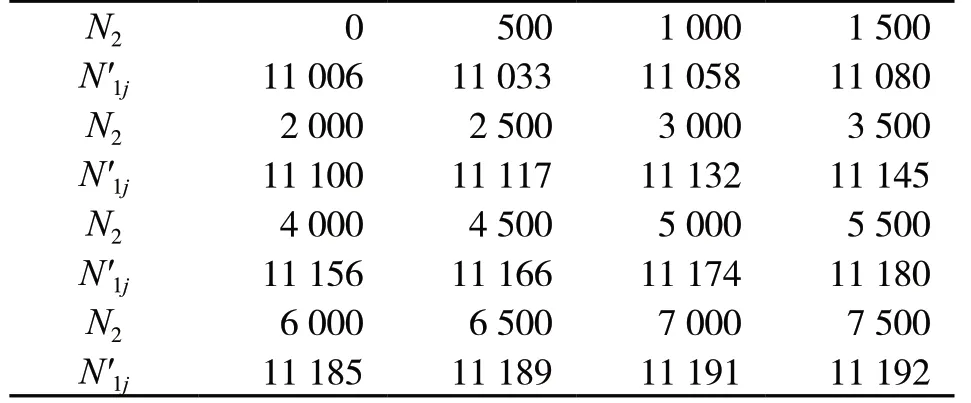
表2 內轉子的二階臨界轉速（單位：r/min）

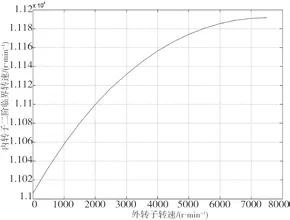
圖6 內轉子二階臨界轉速隨外轉子轉速的變化

4.2 外轉子臨界轉速的計算結果

表3給出了在不同的內轉子轉速下的外轉子一階臨界轉速的計算值。

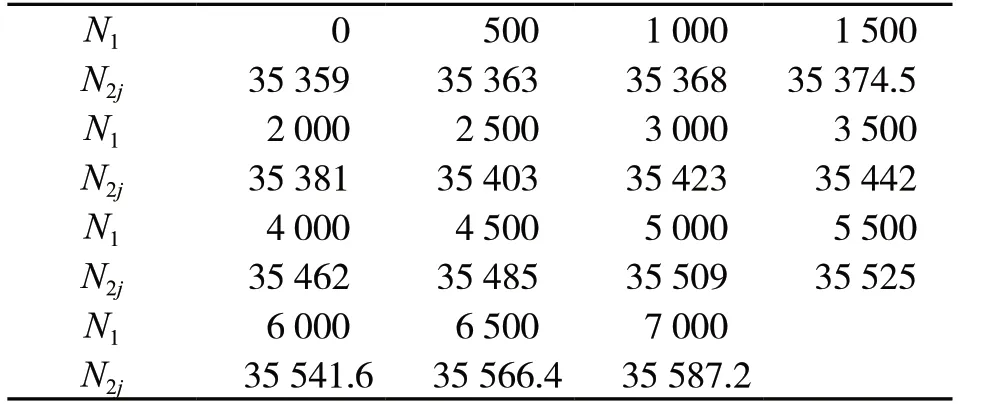
表3 外轉子的一階臨界轉速（單位：r/min）

外轉子一階臨界轉速隨內轉子轉速變化的規(guī)律如圖7所示。

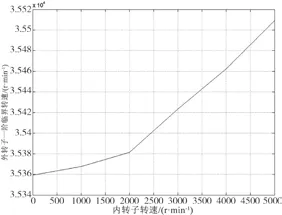
圖7 外轉子的一階轉速隨內轉子轉速的變化

從表3、圖7可以看出，外轉子的一階臨界轉速隨內轉子轉速的上升而上升。原因是隨著內轉子轉速的增加，外轉子和中介軸承相連接的部分動剛度增大，導致了外轉子的一階臨界轉速的上升。

4.3 臨界轉速的振型

在求得了臨界轉速值以后，就可以利用前面的計算結果求解轉子在臨界轉速下的振型，即轉子的撓曲線。求解的方法是先假設初始段的狀態(tài)變量，由于初始段是自由端，所以在位移Χi、撓角θi、彎矩Mi和剪力Qi中，彎矩Mi和剪力Qi為零，設位移Χi為1。

內轉子過一階臨界轉速，而外轉子在一階臨界轉速以下時，內外轉子的撓曲線如圖8所示。

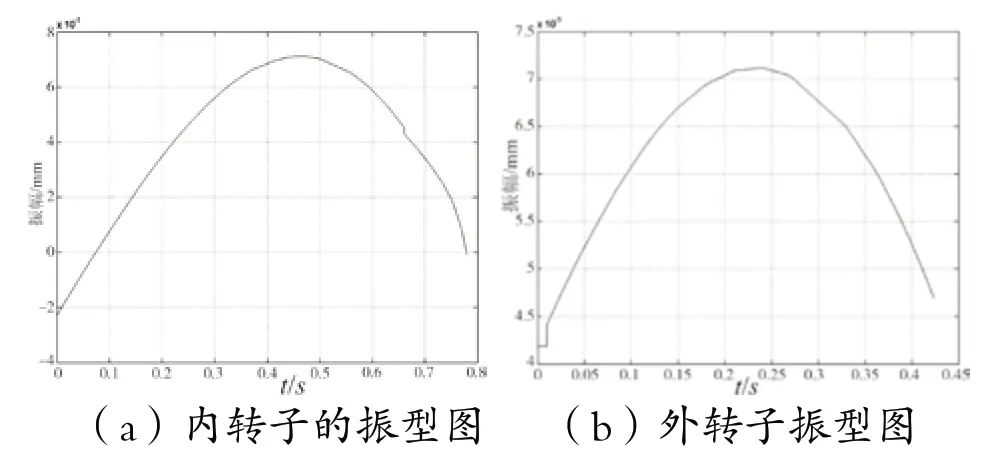
圖8 內轉子過一階臨界轉速時內外轉子的振型（N1=4 500 r/min ，N2=1 000 r/min）

內轉子過二階臨界轉速，而外轉子在一階臨界轉速以下時，內外轉子的振型如圖9所示。

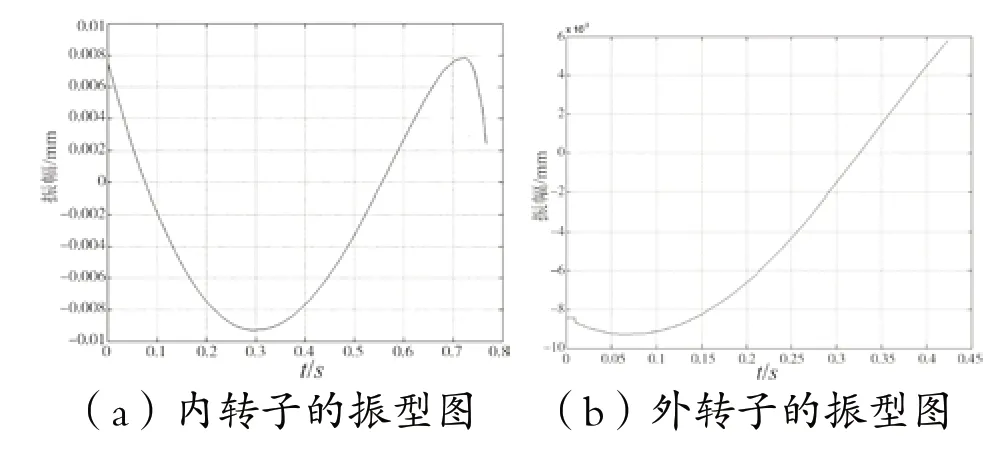
圖9 內轉子過二階臨界轉速時內外轉子的振型（N1=12 000 r/min，N2=1 000 r/min）

內轉子在一階臨界轉速以下，而外轉子在一階臨界轉速以上時，內外轉子的振型如圖10所示。

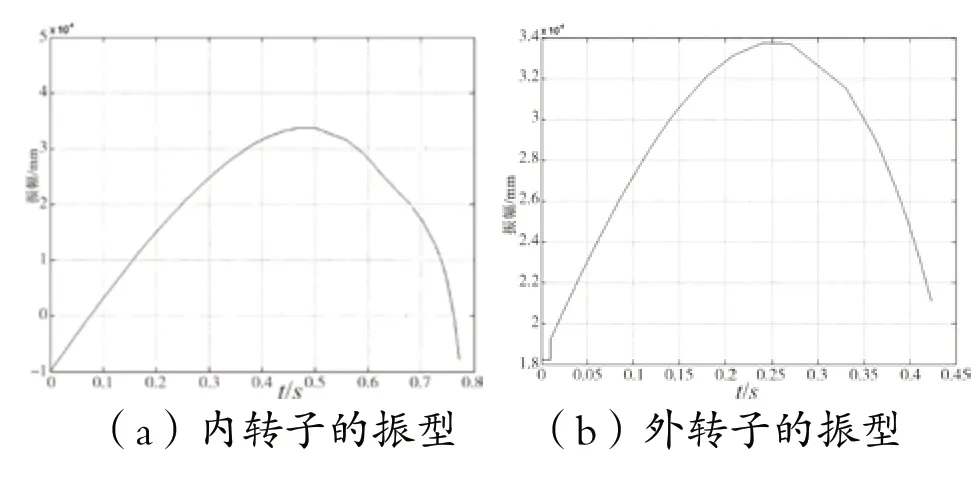
圖10 外轉子過一階臨界轉速時內外轉子的振型（N1=1 000 r/min，N2=35 000 r/min）

5.結論

（1）計算發(fā)現(xiàn)轉速對臨界轉速值的影響規(guī)律：內轉子的一階臨界轉速隨著外轉子轉速的上升先上升、后下降，二階臨界轉速隨著外轉子的轉速增加而不斷增加。外轉子的一階臨界轉速隨著內轉子轉速的增加而增加。

（2）在振型方面，內轉子的振型隨著內轉子轉速的不斷上升而發(fā)生變化，它的相應階的振型與彎曲振動時各階振動的振型基本形同。

（3）對于實際的航空發(fā)動機來說，由于高低壓轉子之間存在著一定的轉速差，因此它的轉速比在一個比較窄的范圍內變化，而不是任意的。在處理這一問題時，可以把內外轉子的轉速變化曲線畫到雙轉子系統(tǒng)的臨界轉速圖譜中，轉速曲線和臨界轉速曲線的交點就是實際各階的臨界轉速。