脈沖展開式飛網質量分布與展開穩定性優化

竺偉梁，龐兆君，司驥躍，杜忠華，程 春

(1. 南京理工大學機械工程學院，南京 210094; 2. 北京機械設備研究所，北京 100854；3. 寧波大學沖擊與安全工程教育部重點實驗室，寧波 315211)

0 引 言

降低空間碎片帶來的危害是航天界的共同愿望，清理空間碎片的空間繩網技術應運而生并得到了快速發展。作為新型的空間繩網技術之一，脈沖展開式飛網利用旋轉離心力抑制繩網回彈，實現繩網在無控條件下持久保形，對加快空間碎片清理具有重要促進作用。由于繩網自身材料和結構特性，在發射后一段時間內網面的展開狀態是不穩定的。脈沖展開式飛網發射展開到網面最大狀態后將經歷回彈-再展開的振蕩階段才能逐漸實現穩定。為便于表述，后文中將該階段稱為回彈振蕩期；將回彈振蕩期內網面從完全展開狀態到回彈后最小展開狀態的降幅稱為最大回彈率。脈沖展開式飛網展開過程中最大回彈率越小、回彈振蕩期越短則網面展開穩定性越高。因此，降低最大回彈率、縮短回彈振蕩期對飛網穩定展開具有重要意義。

繩網優化是提升繩網展開性能的有效方法，根據優化對象可分為繩網發射參數優化、繩網結構優化和網面質量分布優化。其中，繩網發射參數優化相對成熟，通過優化發射速度、發射角度等提升繩網的展開性能。例如Zhang等設計了一種半解析的優化方法，基于簡化的多柔性梁單元全動力學模型優化了繩網的發射參數以擴大繩網在指定位置的展開面積。高慶玉、Chen等基于kriging代理模型和MOEA/D-EGO耗時優化算法建立了空間繩網的多目標優化問題，以繩網發射速度、發射夾角和質量塊質量為優化對象,優化提升了網面展開性能。繩網結構優化是一種較為新穎的繩網優化方法，其通過優化繩網結構來提升繩網的展開性能。司驥躍等采用移動可變形組件法構建了繩網結構優化模型，并用遺傳算法對繩網的構型進行整體優化，使得優化后繩網的有效展開位移提升36.18%。上述兩種繩網優化方法在一定程度上能夠提升網面的展開性能，但也存在一定局限性。繩網發射參數優化是初淺的，未能優化繩網自身的動力學特性。此外，該方法在實際應用中受工況約束影響較大。繩網結構優化則是一種相對深層的優化，通過優化網面自身的動力學特性以提升繩網展開性能。然而，網面結構優化前后網面結構和網面節點質量分布都發生了變化，難以清楚地界定優化指標提升的本質原因，也無法歸納得出一般規律。質量分布優化也是一種動力學特性優化，現有關于柔性體結構的質量分布優化問題多集中在柔性薄板和柔性伸展臂方面，在繩網動力學方面還沒有學者開展相關研究。因此，網面質量分布優化是一種提升繩網展開穩定性的新穎方法。該方法以網面各節點層的質量為優化對象，建立網面各層質量分布規律，提升繩網的展開穩定性。相比于繩網結構優化，網面質量分布優化可歸納出各層節點質量分布對繩網展開穩定性的一般規律。

本文針對脈沖展開式飛網，基于多體系統傳遞矩陣法建立了網面質量分布模型，以縮短回彈振蕩期和降低繩網回彈率為目標優化了網面的質量分布狀態，提升了脈沖展開式飛網的展開穩定性。

1 繩網動力學建模與脈沖展開式飛網展開原理

1.1 繩網動力學模型

繩網動力學建模中，常用的方法有絕對節點坐標法、有限元法和集中質量法。其中集中質量法計算效率高、可移植性強,在繩網優化迭代方面具有較大優勢。本文采用集中質量法，將一條連續的繩段離散成若干質量節點，相鄰節點之間通過并聯的無質量彈簧-阻尼單元互相連接，如圖1所示。相鄰節點間的力可表示為：

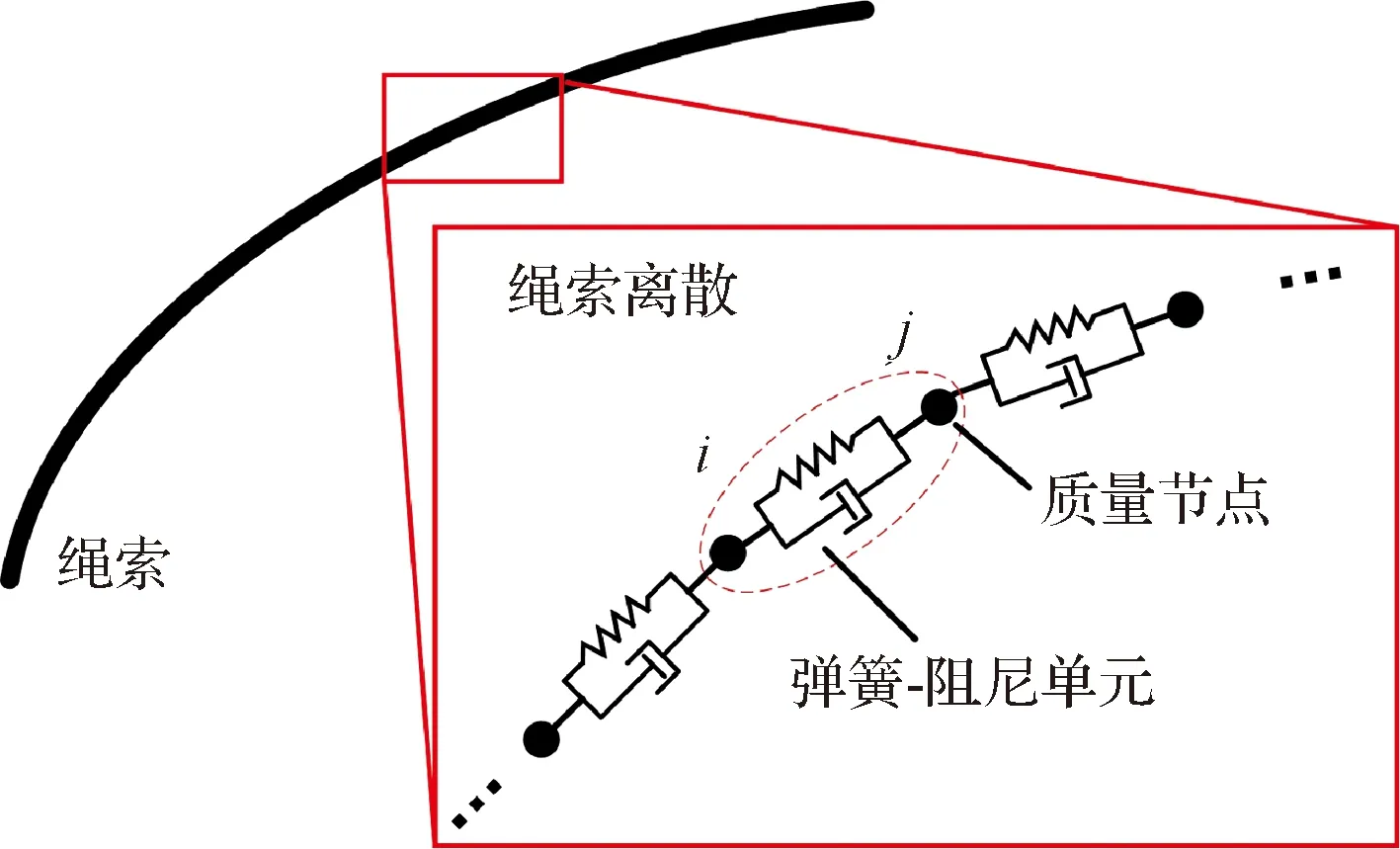
圖1 質點-彈簧-阻尼模型Fig.1 Mass point-spring-damper model

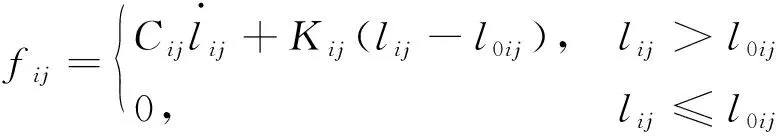
(1)

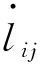
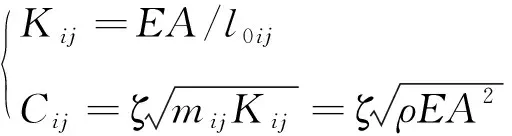
(2)

式中：為繩段的楊氏模量；是繩段的截面積；是阻尼比；是繩段的密度；是節點和之間的繩段質量。

進一步將繩網沿網面結點離散成若干質量節點和彈簧-阻尼單元，并用無向圖=(,)進行表示，如圖2所示。其中，頂點集={1,2,3,…,}代表繩網上離散的質量節點集，邊集代表繩網上相鄰節點之間的連接繩段集。網面上各節點之間的連接情況可由鄰接矩陣()表述，其組成元素為，則繩網上節點的受力可表示為：

圖2 繩網模型Fig.2 Net model

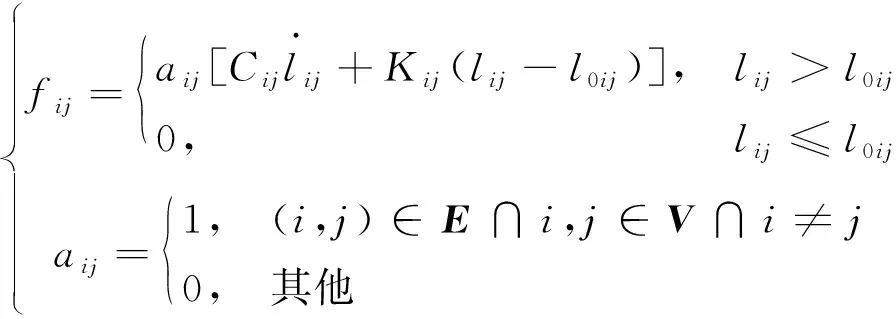
(3)

1.2 脈沖展開式飛網展開原理

脈沖展開式飛網是一種展開過程中利用單次脈沖實現持續保形的空間繩網，飛網展開過程可分為兩個階段：第一階段為牽引體彈射階段，牽引體以一定發射角度進行彈射并帶動繩網在空中展開;第二階段為單脈沖作用階段，當飛網面積展開至60%后，牽引體產生切向脈沖力致使網面旋轉，并利用旋轉離心力實現持續保形，如圖3所示。

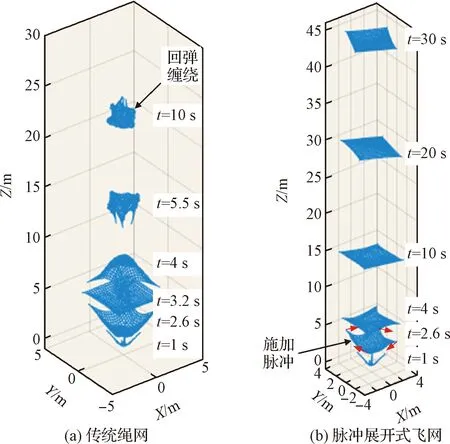
圖3 傳統繩網與脈沖展開式飛網展開過程對比Fig.3 Comparison of the unfolding process between the traditional net and the single-pulse-deployed net

相比于傳統繩網展開，脈沖展開式飛網可避免回彈纏繞，并持續保持網面展開狀態。然而，脈沖展開式飛網首次展開至最大值后將經歷回彈-再展開的回彈振蕩期，如圖4所示。回彈振蕩期內飛網展開狀態不穩定、展開率波動較大將影響對目標的可靠抓捕。

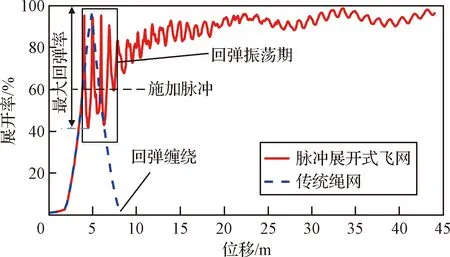
圖4 傳統繩網與脈沖展開式飛網的展開率對比Fig.4 Comparison of the unfolding ratio between the traditional net and the single-pulse-deployed net

優化網面的質量分布是一種理想的優化方式，從飛網自身動力學特性出發，調整網面質量分布以降低網面回彈率、提升網面展開穩定性。該方法無需調整繩網發射參數，因此對一些繩網發射條件嚴苛的工程具有更好的適應性。

2 質量分布模型

實際應用中，網面結構較大、網格數多、自由度大，難以直接對網面質量分布進行優化求解。此外，較多的網格數將導致質量分布優化問題中的優化變量過多，質量分布最優解的收斂效果難以保證。因此需根據繩網結構特性和網面質量分布規律建立網面質量分布優化模型，降低優化變量個數。

繩網由多個繩段相互連接組成，繩段的受力和運動特性與繩網的動力學特性有著較大的相似性。為便于理論推導，首先建立一維繩段模型，并推導質量分布對繩段拉伸和回彈問題的影響規律。隨后將一維繩段的質量分布規律推廣至脈沖展開式飛網，并建立網面質量分布模型，從而將多優化變量的網面質量分布問題轉化為單一優化變量模型以提升多目標優化求解效率。

2.1 基于傳遞矩陣的一維繩段質量分布模型推導

多體系統傳遞矩陣法是一種高效的多體系統研究方法，在兵器、航空、航天等領域得到廣泛應用。采用矩陣形式對離散的繩段模型進行表述，并通過矩陣累乘得到繩段的動力學傳遞矩陣。多體系統的響應可由模態主振動疊加而成，若某階模態下多體系統的固有頻率為，則對應的狀態量可表述為：

=ei

(4)

式中：i為虛數單位；稱為模態坐標下的狀態量。

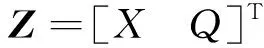
=-1

(5)

式中:表示第個物體。

繩段受外力拉伸擾動后，繩段的最大回彈量與其最大拉伸量成正相關，因此可選取繩段最大拉伸量作為觀測對象。繩段受擾動后在短時間內即可達到最大拉伸狀態，該過程中比例項起主導作用。為便于分析，在短時間內可略去阻尼項。因此，繩段模型可進一步簡化為彈簧質點模型。對于一根兩端自由且左右對稱的一維繩段，在左右對稱擾動下可構建一端固定、另一端自由的多體系統動力學模型，如圖5所示。其中固定端代表繩段的中心點，模型中各離散節點質量分別為，，…，，∈{2,4,6,…,-2}。繩段的質量分布通過調節離散節點的質量實現。

圖5 繩段動力學模型Fig.5 Dynamical model of rope segment

將一個彈簧和一個節點視為一個單元，該單元的傳遞矩陣為：

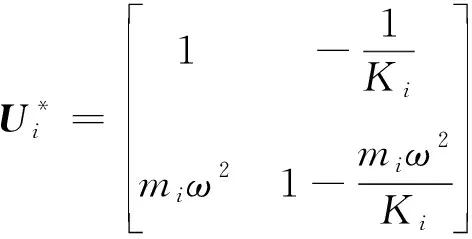
(6)

式中：為節點的質量；為系統的固有頻率；為彈簧的彈性系數。

對于兩個相鄰的單元，其傳遞矩陣為：

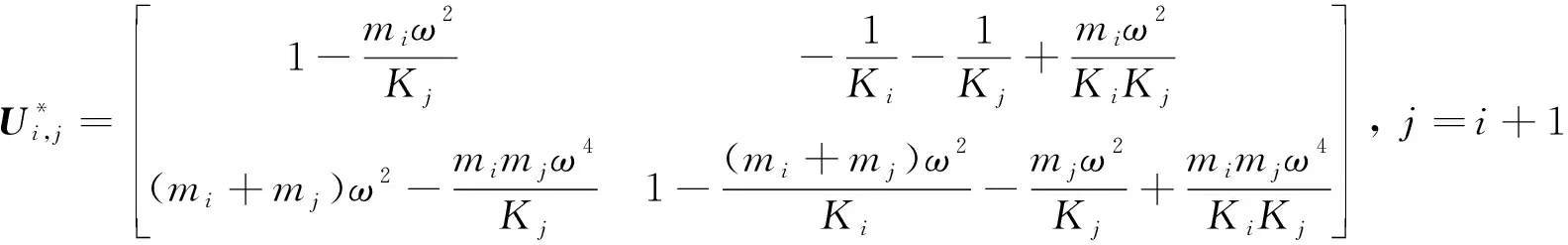
(7)

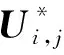
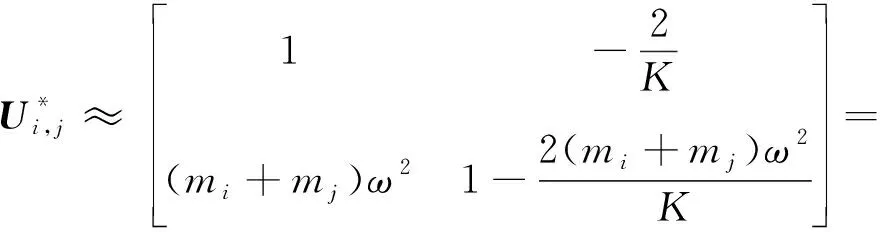
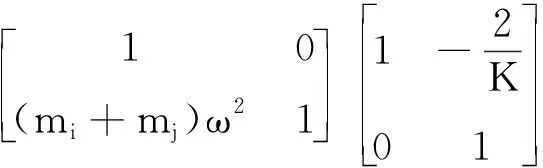
(8)

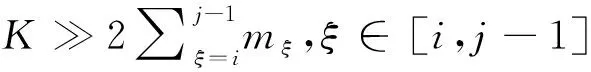
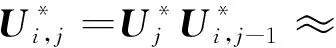
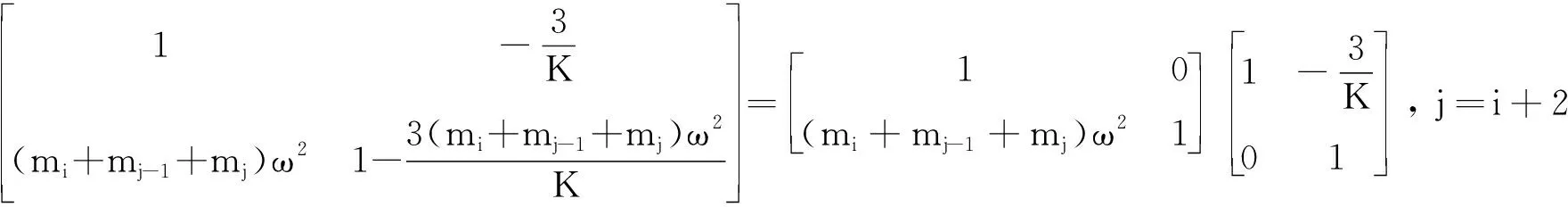
(9)

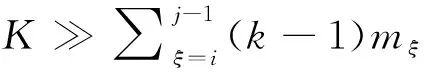
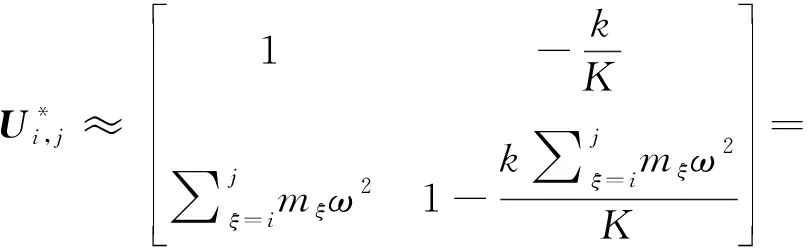
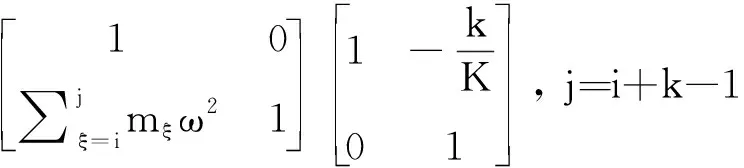
(10)

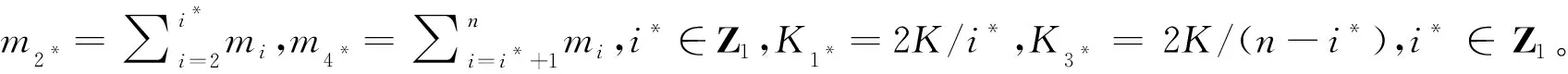
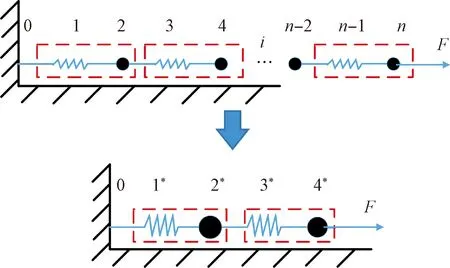
圖6 等效鄰接單元模型Fig.6 Equivalent model to adjacent element

(11)

在擾動力的作用下，鏈式系統的傳遞矩陣可增廣至3×3的矩陣，對應的狀態量也增廣至3×1的列向量，如式(12)所示。

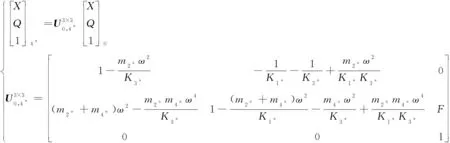
(12)

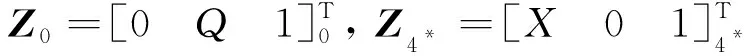
4=

(13)

當1,3?2,4,且min(1,3)>2時：

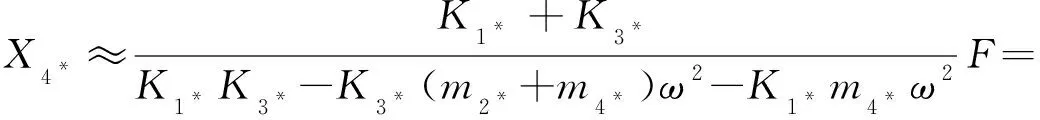
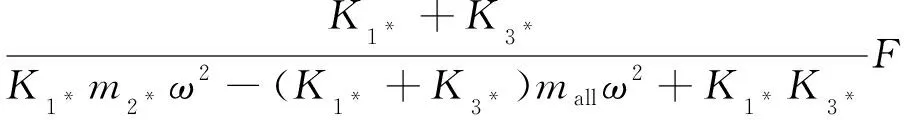
(14)

顯然，4是關于2的近似反比例遞減函數，即繩段的最大拉伸量是關于2的減函數。其中，=2+4為繩段的總質量。

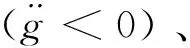
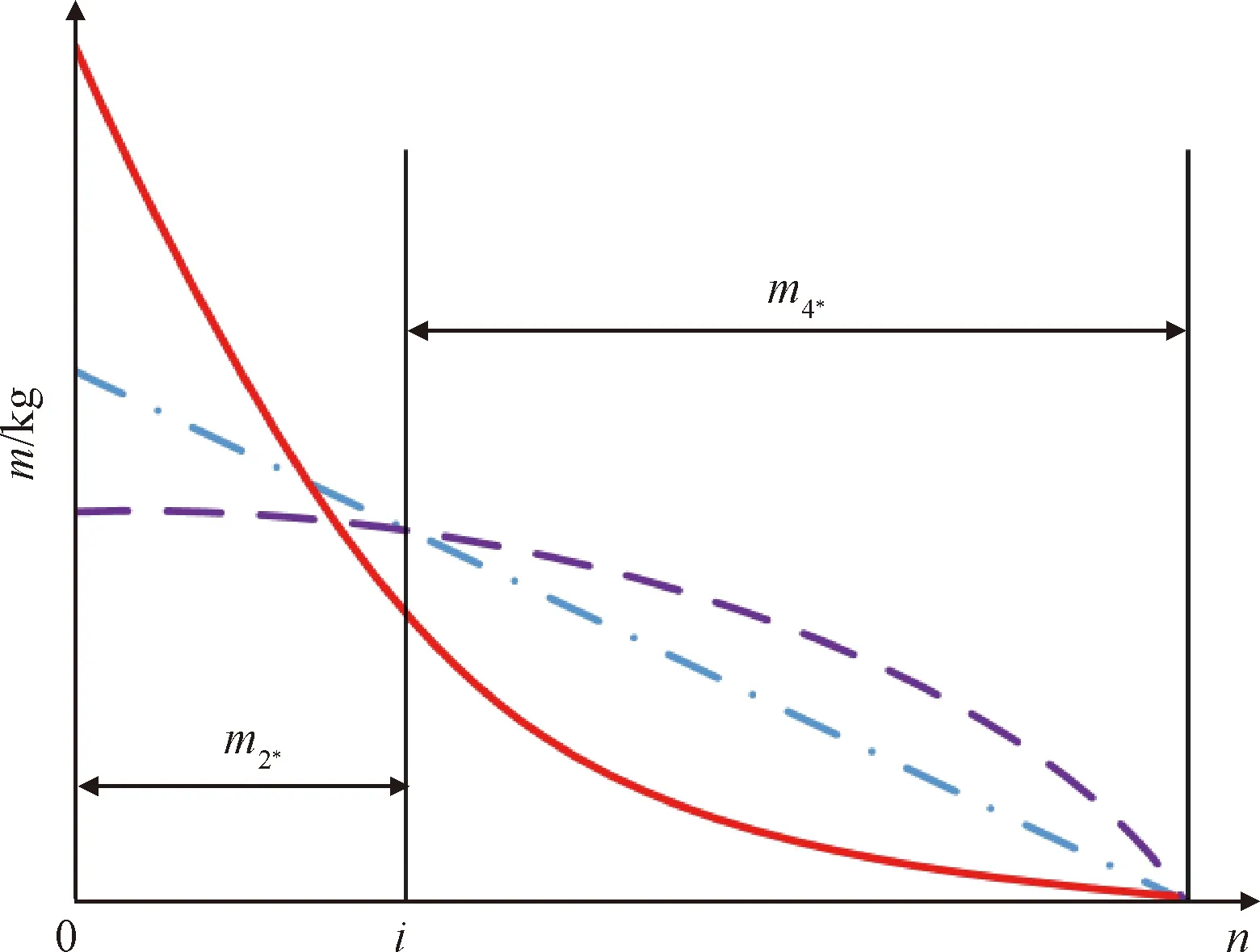
圖7 三種繩段的質量分布函數Fig.7 Three mass distribution functions of the rope

為驗證一維繩段模型推導結果的正確性，現基于MWorks和Matlab進行驗證。設置8個串聯的彈簧阻尼質點單元，為避免節點質量過小導致的積分誤差，將繩段總質量分為兩部分：一部分為各節點均分的基礎質量，另一部分為質量分布規律決定的可變質量。具體參數設置詳見表1。

表1 仿真參數Table 1 Simulation parameters

分別建立線性遞增、均勻分布、凸形遞減、線性遞減和凹形遞減共5組質量分布，各組可變質量分布情況如圖8所示。

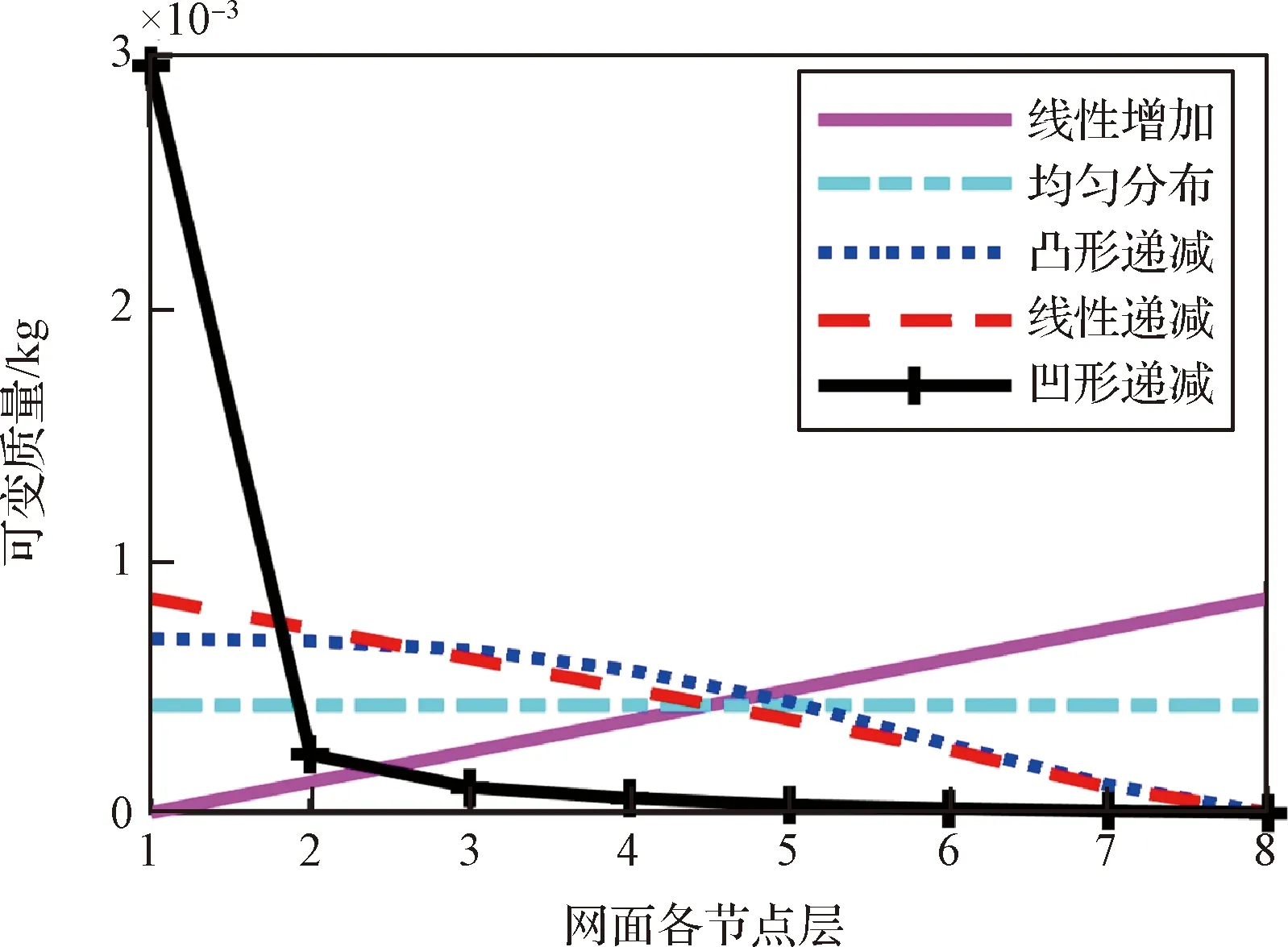
圖8 5種質量分布中可變質量的分布Fig.8 Five distributions of assignable mass

圖9 不同質量分布下繩段的最大伸長量對比Fig.9 Comparison of maximum elongation of rope segments with different mass distributions

2.2 網面質量分布模型建立

繩網由若干繩段連接而成，具有類似繩段的運動特性。將繩段的質量分布規律拓展至二維繩網，并通過數值仿真驗證網面質量分布規律。借鑒一維繩段模型，通過集中質量法將網面按照節點進行離散，并將節點從網面中心向邊緣進行逐層劃分，如圖10所示。為避免節點質量過小導致的積分誤差，將繩網的總質量劃分為基礎質量和可變質量兩部分。在繩網總可變質量守恒條件下通過調節各層節點的可變質量實現網面質量分布調整。

圖10 繩網節點層Fig.10 Tiers of the mass-nodes upon the net

繩網各層節點數可表示為：

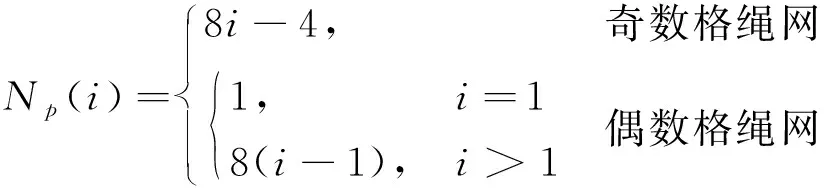
(15)

式中：∈。對于節點總層數為的繩網，第層的節點質量為()。任意兩不同層的節點質量(),()為兩個相互獨立的變量。因此，節點總層數為的繩網優化變量個數為。結合式(15),繩網的可變總質量為：

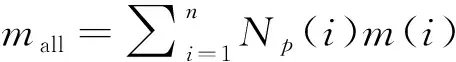
(16)

不失一般性，以邊長為5 m，單邊15格的方形Kevlar繩網為例。從網面中心逐層向外，將網面各層節點質量按照線性遞增、均勻分布、凸形遞減、線性遞減和凹形遞減五種質量分布規律賦值，并保證繩網可變質量守恒，如表2所示。其中，繩網總質量為0.2448 kg，基礎質量0.1224 kg，可變質量0.1224 kg。控制牽引體彈射速度為5 m/s，牽引體質量為350 g，發射偏角為30°，脈沖速度10 m/s，繩索的彈性模量為70 GPa，泊松比為0.3。

表2 五種網面質量分布規律Table 2 Five kind of net surface mass distribution models

五種網面質量分布規律對應的網面展開狀態如圖11所示。繩網質量分布對最大回彈率的影響規律基本與一維繩段問題中所得規律一致，在線性遞增、均勻分布、凸形遞減、線性遞減和凹形遞減五個網面質量分布規律中，凹形遞減的質量分布規律所對應的網面展開最穩定。五種網面質量分布規律所對應的網面最大回彈率依次遞減，分別為74.15%，67.50%，60.10%，58.23%，35.57%。

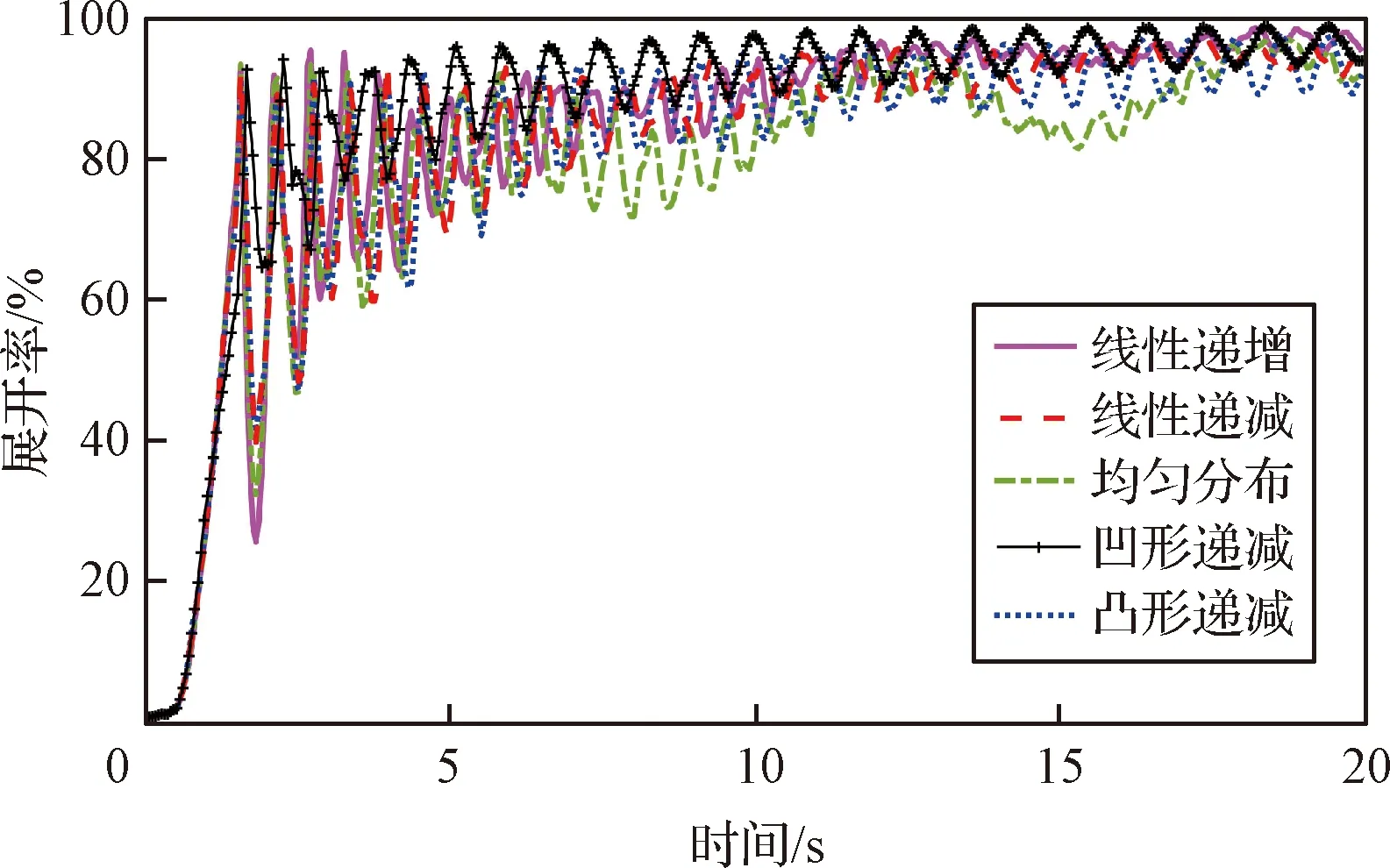
圖11 五種質量分布狀態下脈沖展開式飛網展開率對比Fig.11 Comparison of unfolding ratio of the single-pulse-deployed net under five mass distributions

基于網面節點分層特性，可將各層節點質量設為優化變量進行優化，對于節點總層數為的繩網則有個待優化的變量。實際工程中通常網面層數較多，導致繩網質量分布優化問題中優化變量過多，最優解難以快速收斂。因此，需要根據網面質量分布規律建立網面質量分布模型，降低繩網質量分布優化問題中優化變量的個數。由前文分析可知，凹形遞減分布是一種較優的質量分布規律，故以此對網面質量分布模型進行探究。

第一象限內的反比例函數(-)+是一種典型的凹形遞減函數，可通過調節增益、相位偏移量和常數項得到不同曲率的凹形遞減函數。根據網面節點層號離散的特點，將反比例函數改寫為離散形式，得到網面質量分布模型：

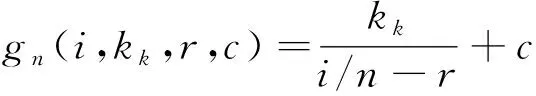
(17)

式中：為節點總層數；為節點層編號，根據對網面各層節點質量()進行賦值。為滿足?∈[1,],(,,,)≥0，需保證0<<1且(=,,,)≥0。此時，網面質量分布模型中未知自變量為,,。引入邊界條件：(=,,,)=0，即有：

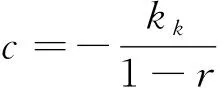
(18)

將式(15)，式(16)代入式(18)得到：

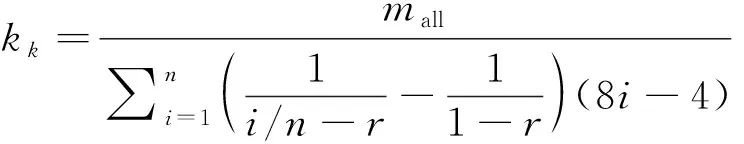
(19)

對于給定可變總質量為和繩網節點總層數為的繩網，是關于相位偏移量的單值函數。故式(17)可進一步改寫為：

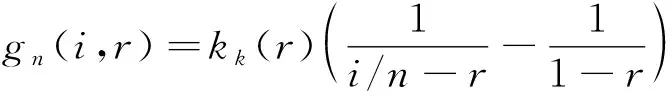
(20)

式中：∈(0,1)。此時，網面質量分布模型中未知自變量僅為相位偏移量。

3 脈沖展開式飛網多目標優化

脈沖展開式飛網展開過程中，以最大回彈率和網面回彈振蕩期(數值上按照展開率均值穩定在95%以上所需的時間進行計算)為目標函數進行優化。

將網面質量分布模型和遺傳算法相結合的優化方法(后稱本文方法)，僅需優化單一變量即可得到優化的網面質量分布結果。該多目標優化可表述為：

(21)

式中：()代表相位偏移量與目標函數集[,]之間的映射；()為關于參數的凹形遞減質量分布函數；為繩網的可變總質量。

繩網多目標優化問題中，和之間具有沖突性，難以找到一個使得兩目標函數均為最優的解。因此，采用Pareto非劣解對優化結果進行表述。以網面邊長為5 m、單邊15格的方向繩網(=8)為例，質量均勻分布為初始解進行多目標優化。

為對比本文質量分布模型下的多目標優化效果，設置對照組：根據網面節點分層特性，將每層的節點質量設置為優化變量，并采用遺傳算法進行逐層優化，優化過程中優化變量總數為。對照組可表述為：

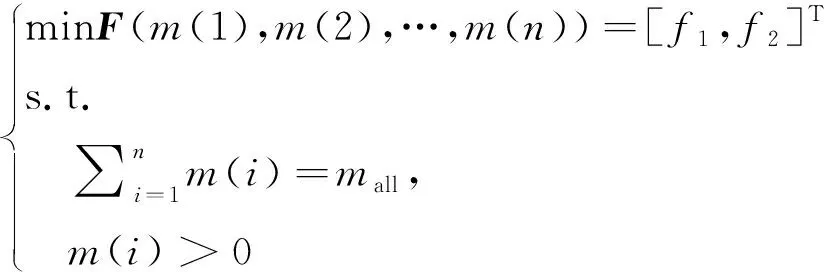
(22)

經多目標優化分別得到4組Pareto非劣解集，如圖12所示。由于繩段單向受力特點導致的繩網動力學映射不連續性，使得遺傳算法優化得到的Pareto非劣解呈集散狀分布并伴隨多個重疊的非劣解。圖中點的位置代表目標函數的值，點的大小代表解的重疊度。在相同且較少的遺傳代和種群數量條件下,本文方法能夠更快地收斂得到更優的解；而對照組中，直接采用遺傳算法對網面節點質量進行逐層優化的方法則需要更多遺傳代和種群數量才能收斂得到較優解。

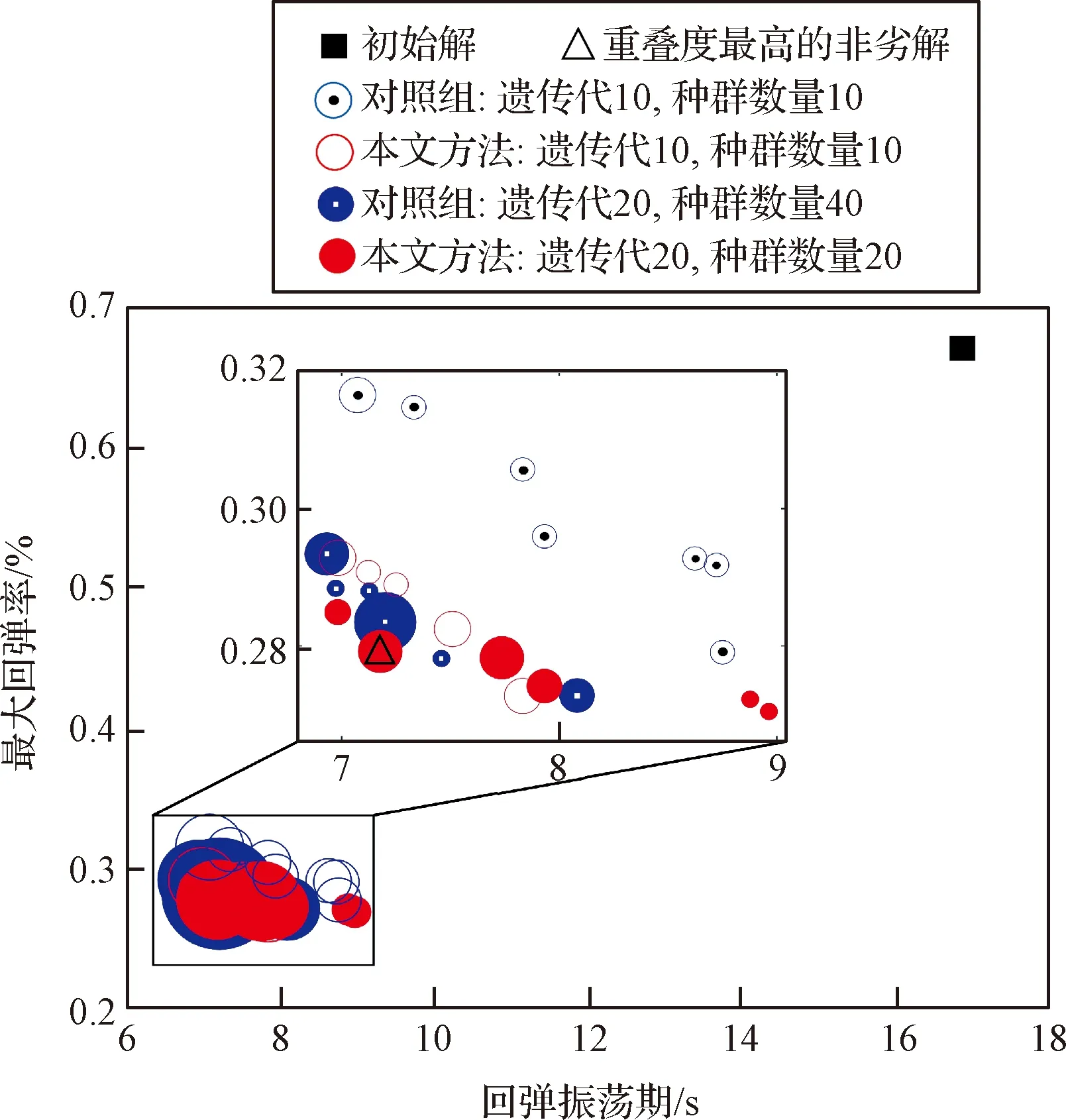
圖12 邊長為5 m，單邊15格的方形繩網的Pareto解集Fig.12 Pareto solution set for a square rope net with side length 5 m and 15 grids on each side

本文方法優化后,飛網在7 s至9 s內恢復穩定狀態，最大回彈率控制在29.5%以內。從初始解到較優解的提升是由網面質量分布模型實現的，提升幅度較大；在較優解的基礎上繼續增加迭代次數所獲得的網面展開性能提升是由遺傳算法對參數的進一步優化實現的，提升幅度較小。最大回彈率由網面質量均勻分布狀態下的67.5%降低至網面質量分布優化后的28%；回彈振蕩期由網面質量均勻分布狀態下的17 s縮短至網面質量分布優化后的7.2 s。本文方法求得的非劣解對應的網面各層質量分布基本重合，且越往網面邊緣質量差異越小，如圖13所示。

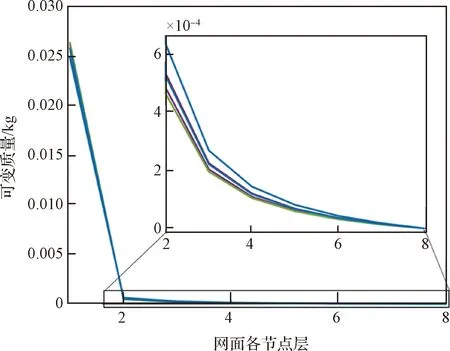
圖13 本文方法求得的網面各層可變質量分布Fig.13 Mass distributions corresponding to the Pareto set

選擇本文方法中重疊度最高的非劣解作為最優解并提取其對應的網面展開狀態和展開率曲線，如圖14和圖15所示。從網面展開狀態上看：最優解對應的網面展開狀態良好，網面在展開后基本處于平整狀態，僅在最大回彈點時網面中心處有略微回彈;而質量分布均勻的脈沖展開式飛網展開狀態相對不穩定，網面的平整度較差，尤其是在最大回彈點,網面出現較大凹陷，且網面邊角處有較明顯的折疊，如圖14所示。從網面展開率方面看：優化后脈沖展開式飛網的回彈現象得到了較好的抑制，發射后網面展開率快速上升且波動小，僅在3 s內即可使得網面展開率穩定在80%以上，網面回彈振蕩期縮減至7.2 s內;而對于網面質量均勻分布的繩網則需要在10 s后展開率才能穩定在80%。此外，優化后的脈沖展開式飛網具有更好的展開穩定性，脈沖作用后展開率處于小幅波動狀態并逐漸向完全展開狀態收斂；而網面質量均勻分布的脈沖展開式飛網仍有周期性的大幅度振蕩，難以快速穩定，如圖15 所示。因此在相同發射工況下，優化后的脈沖展開式飛網具有更好的展開穩定性。

圖14 優化前后繩網展開狀態對比Fig.14 Comparison of the deployment status of the net before and after optimization

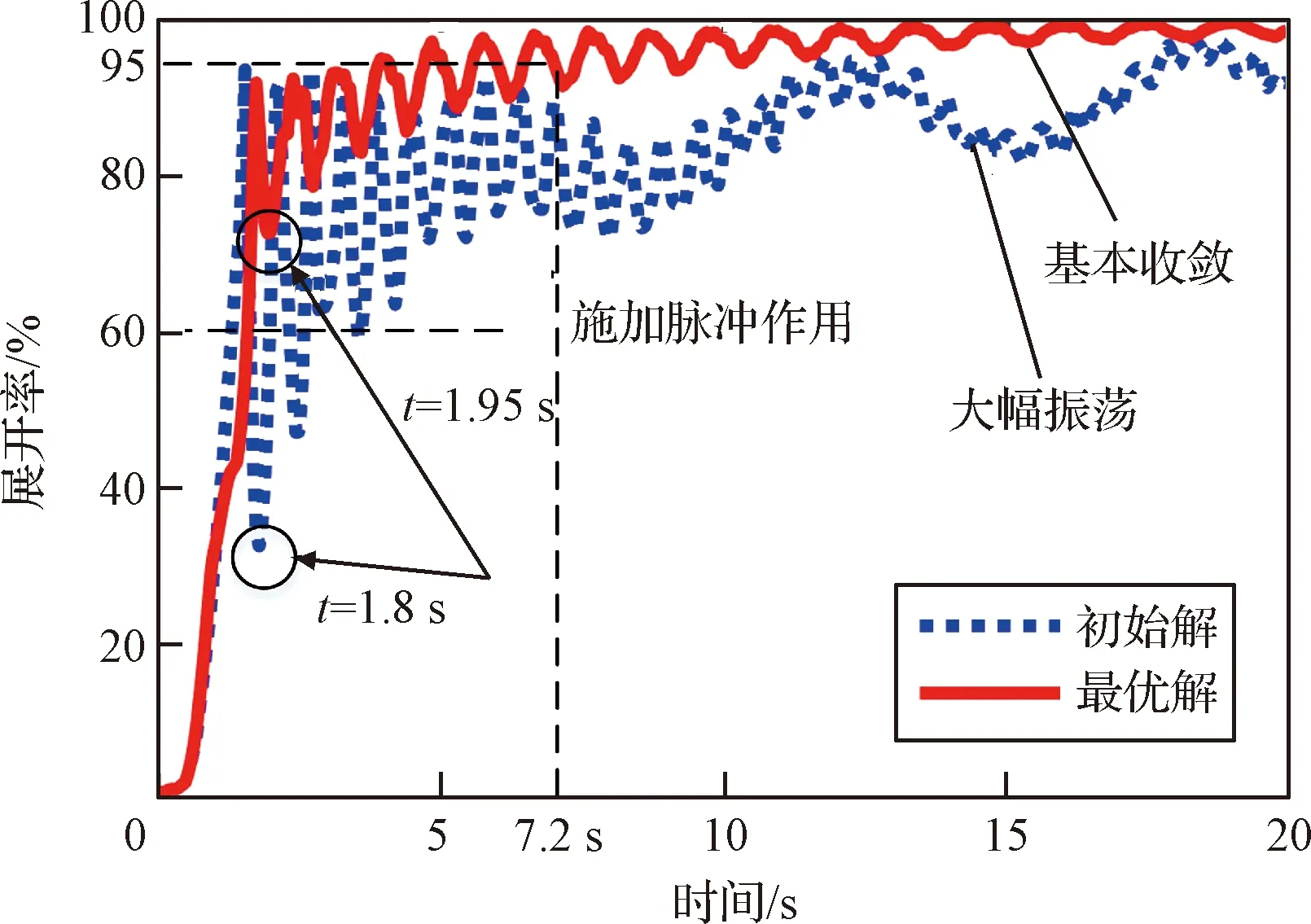
圖15 優化前后繩網展開率對比Fig.15 Comparison of the unfolding ratio of the net before and after optimization

同理，采用本文方法對常見的網面節點層數為8～15的脈沖展開式飛網進行網面質量分布優化，得到不同層數繩網所對應的非劣解集合。由相位偏移量的邊界條件0<<1，各對應的非劣解可改寫為：

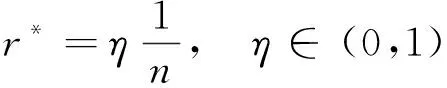
(23)

式中：為小于1的正向比例系數。

由非劣解集合分析得到關于非劣解的正向比例系數∈[0.965,0.985]，如圖16所示。進一步由線性回歸得的線性表達式為：

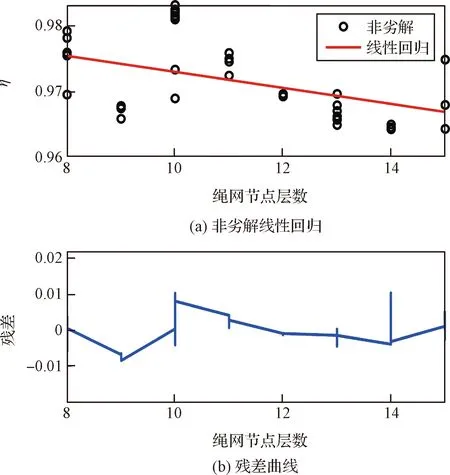
圖16 不同層數規格繩網的η的回歸分析Fig.16 Regression analysis of η with different nets

=-0001225+09852

(24)

殘差分布在±0.01之間。將式(23)、式(24)代入式(19)和(20)得網面質量分布經驗式：

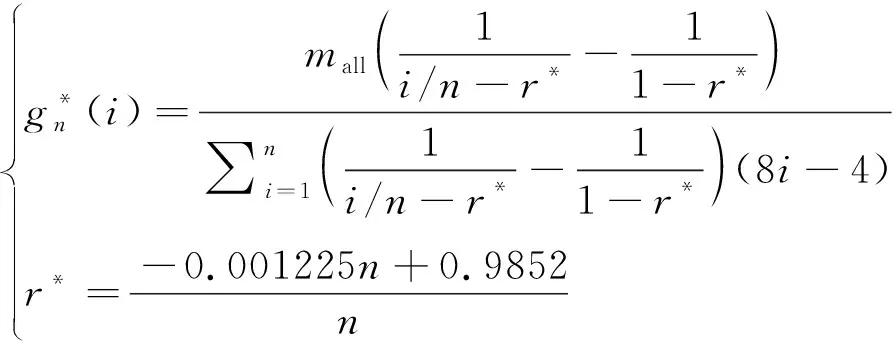
(25)

即對于給定的繩網節點層數為的繩網，可通過代數運算得到優化的網面質量分布。

取={8,9,…,15}分別計算脈沖展開式飛網的網面質量分布經驗式，并代入繩網動力學映射與多目標優化、質量均布對應的網面展開情況進行對比。圖17給出了單邊25格繩網=13的對比結果，網面質量分布經驗式具有良好的繩網展開狀態，與多目標優化最優解所對應的繩網展開狀態基本一致。其余規格繩網的對比結果與之相同，不再贅述。

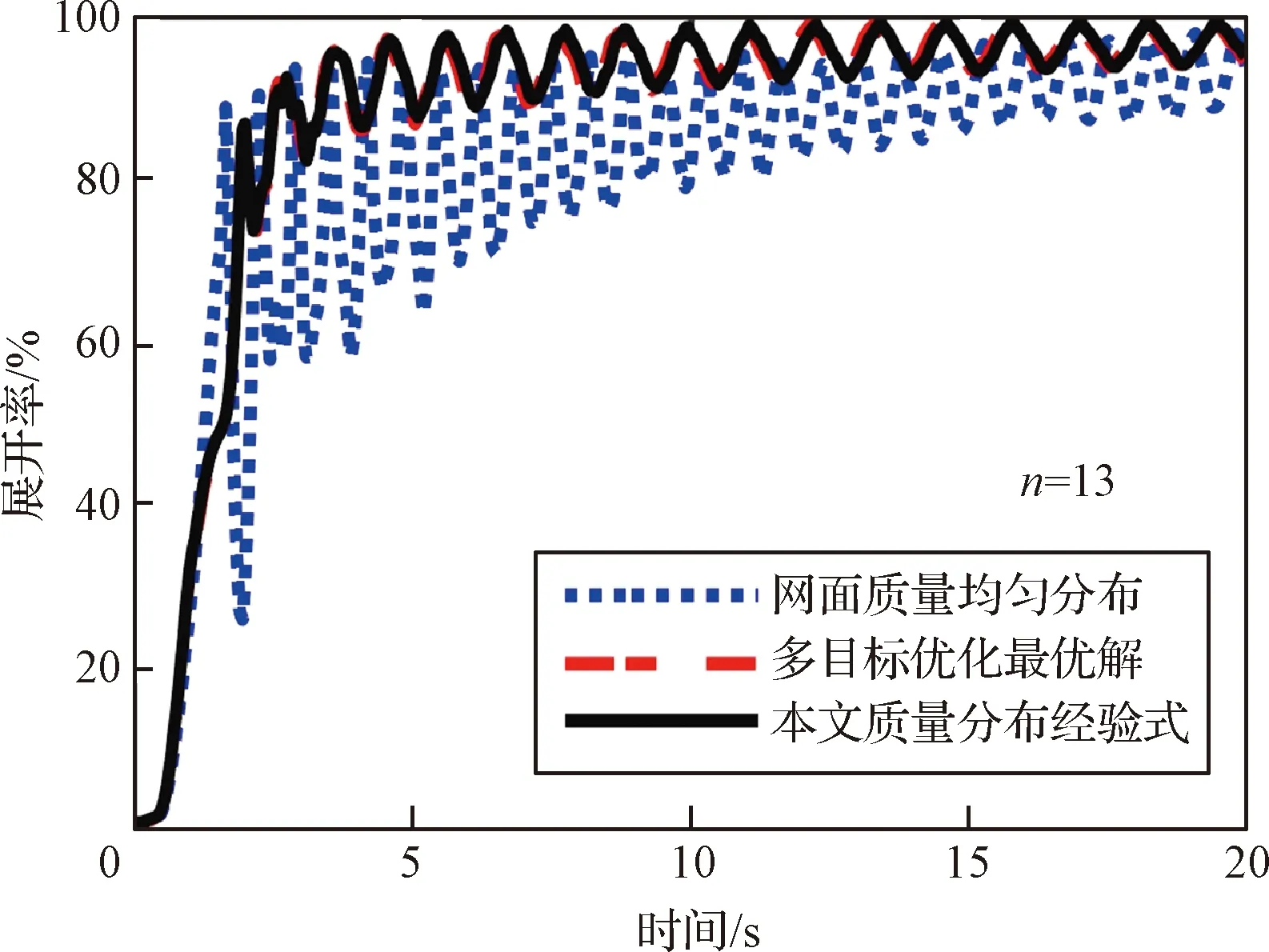
圖17 脈沖展開式飛網的展開率對比Fig.17 Comparison of the unfolding ratios of the single-pulse-deployed net

4 結 論

針對脈沖展開式飛網展開后仍存在的較大回彈問題，本文從網面質量分布角度優化提升飛網展開時的穩定性。研究結果表明：1)基于傳遞矩陣方法和集中質量法推導得到的一維質量分布規律在二維網面中仍然成立，在線性遞增、均勻分布、凸形遞減、線性遞減和凹形遞減五個質量分布模型中,凹形遞減的網面質量分布所對應的網面展開穩定性最好。2)本文基于反比例函數建立的網面質量分布模型對不同規格繩網均具有較好的適應性，可快速調節相位偏移量,得到不同的網面質量分布狀態且極大地降低了網面優化問題中優化變量的個數，提升了繩網優化問題的求解效率。3)最大回彈率由網面質量均勻分布狀態下的67.5%降低至網面質量分布優化后的28%；回彈振蕩期由網面質量均勻分布狀態下的17 s縮短至網面質量分布優化后的7.2 s。4)網面質量分布經驗公式所對應的網面展開狀態良好，與多目標優化最優解基本一致。