線性壓縮機直線電機超低振動輸出特性研究

蔣珍華，項漢楨，丁 磊，黃 政，陸 志，劉少帥，吳亦農，曲曉萍

(1.中國科學院上海技術物理研究所，上海 200083；2.中國科學院大學，北京 100086)

0 引 言

近年來低溫制冷技術飛速發展，在航天紅外探測領域的應用越來越廣泛。一方面，制冷型紅外探測器必須在低于某一溫度下才能正常工作，獲得較高的靈敏度、分辨率和信噪比[1-2]；另一方面，低溫環境可以減輕探測視場內零部件的熱輻射背景干擾，提高探測靈敏度[3]。因此，對長壽命、高效率、低振動、輕量化的低溫制冷機的研究尤為迫切。

低溫制冷機由壓縮機和膨脹機組成，壓縮機是制冷機的心臟，為系統提供動力。壓縮機中的電機帶動活塞做直線往復運動為冷指提供壓力波，是電功轉換為機械功的重要部件，負載剛度與動子質量的匹配性決定了電機效率，進而影響制冷機效率[4-5]。文獻[6]用等效磁路法分析了動磁式線性壓縮機的電機結構，得出電磁推力與勵磁電流和電動機幾何尺寸等參數的相關數學關系式，為動磁式壓縮機的設計奠定了基礎。但動磁式壓縮機的徑向顫振較大，應用較為局限。本文以低顫振的動圈式壓縮機為例，進行等效磁路分析，得到了電機效率與各參數之間的關系式，并與有限元仿真相結合，獲得了電機各參數對電機效率影響的數值規律。

壓縮機設計時通常采用對置式活塞設計方式以抵消軸向顫振力，由于兩側電機的磁性能、活塞的尺寸、動子的質量等無法保證完全一致，實驗測試中仍會發現壓縮機有比較明顯的軸向顫振，這種顫振將影響紅外載荷的探測精度[7]。文獻[8]設計了一種被動減振器來抑制斯特林制冷機的軸向顫振，發現只有當減振器與制冷機的固有頻率與驅動頻率均相等時，才能消除斯特林制冷機的顫振。此種方法需要額外增加體積和質量，且對被動減振器的固有頻率精度要求高，若存在諧振偏差，減振效果將受到影響。制冷機安裝至整機后，會影響減振器安裝路徑上的阻尼，使其固有頻率發生偏移，導致減振效果變差。本文依據理論分析，從根源入手，分析壓縮機產生顫振的具體原因，模擬分析了電機運行狀態參數對顫振力的量化影響，給出了抑制顫振力的調整方法并進行了實驗驗證，從壓縮機本體出發將顫振降至較低水平。

1 雙動圈直線電機設計

1.1 雙動圈式直線電機結構

本文設計的雙動圈式直線電機結構如圖1所示。電機的靜子部分由上下主磁鋼、上下端部磁環、中間磁環、內外磁極組成，其中上下主磁鋼徑向充磁，中間磁環和上下端部磁環軸向充磁，內外磁極采用高磁導率的軟鐵材料。電機的動子部分由活塞、活塞軸、雙段線圈、柔性板簧組成，其中活塞軸與雙段線圈通過線圈骨架螺接在一起，套在活塞軸上的柔性板簧通過軸端螺母固定，整體構成彈簧振子系統[9]。線圈通入正弦交流電時，受安培力作用，帶動壓縮活塞進行往復直線運動，在壓縮腔內形成壓力波。

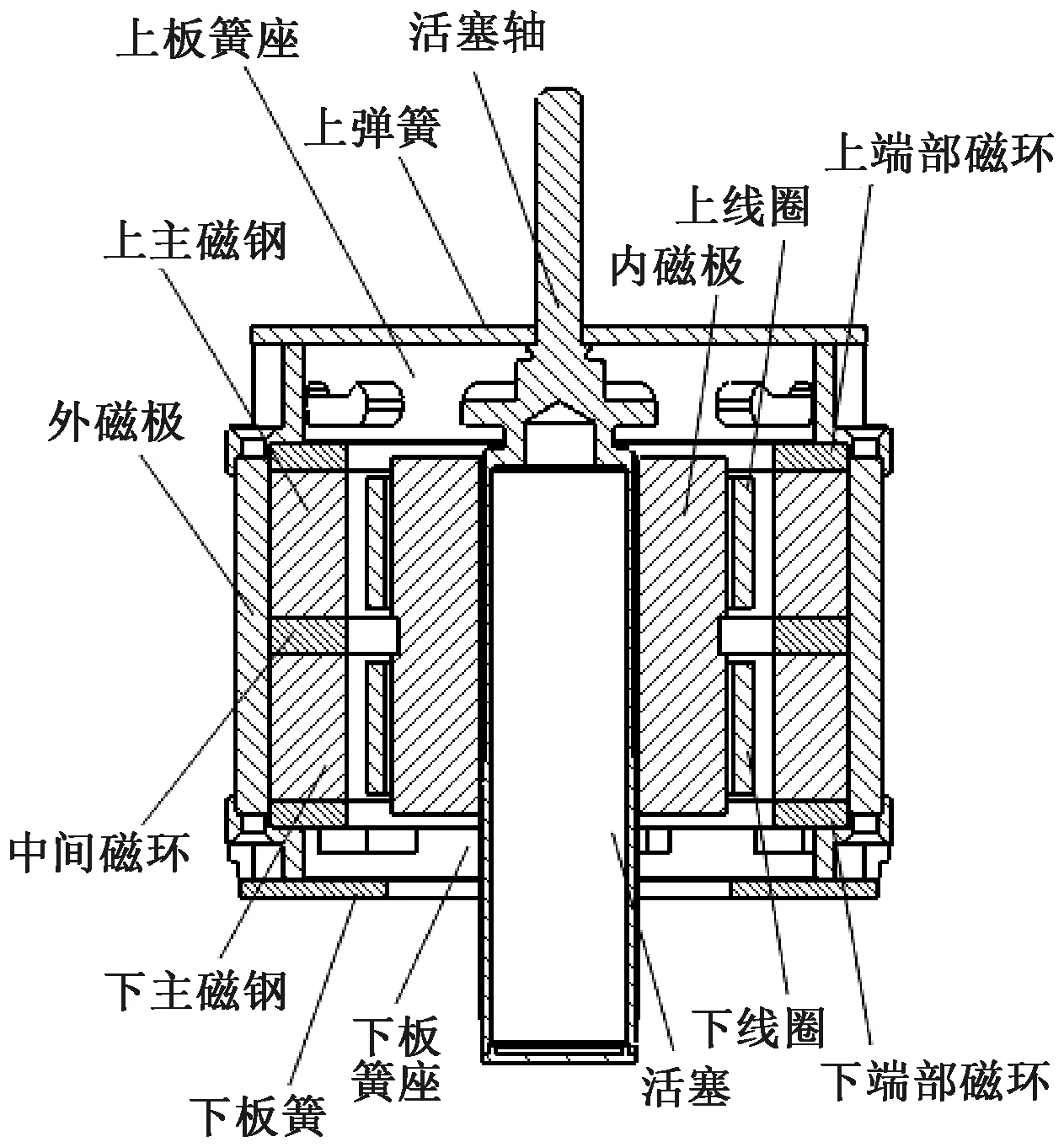
圖1 雙動圈式直線壓縮機結構示意圖

磁鋼的這種排列組合為Halbach陣列[10-11]，可以在有限的體積內較大地增加單側磁場強度。對比相同磁路尺寸的Halbach陣列磁路和非Halbach陣列磁路，當所有永磁體牌號均為N50H時，如圖2所示，非Halbach陣列氣隙磁場區域內特定點處的磁感應強度為368 mT，Halbach陣列氣隙磁場區域內相同點處的磁感應強度為758 mT，磁場強度增加了106%，磁場強度得到了顯著的提升。同時由表1可知，非Halbach陣列電機外側發散在空間特定點的磁感應強度為336 mT，相同點處Halbach陣列的磁感應強度為154 mT，下降了54%，說明Halbach陣列磁鋼減小了電機的漏磁，可以大幅降低磁干擾對探測器重要元器件的影響。

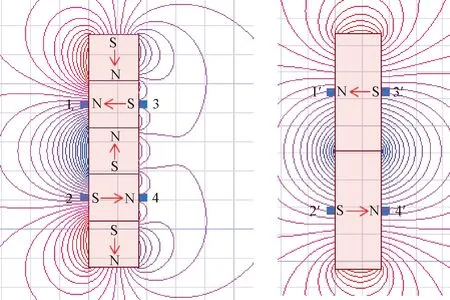
圖2 永磁體陣列磁感應線圖

表1 不同磁鋼陣列關鍵點處的磁感應強度

由電機組件的磁路結構及磁感應線分布可知，線圈通入交流電進行往復運動的過程中，主要受到安培力的作用，安培力推動線圈進行軸向運動。為了進一步分析安培力F=BIL與電機效率的關系，建立如圖3(a)所示的電機模型。上下線圈串聯，但繞向相反，當其通入正弦交流電時，兩個線圈產生的磁動勢NI大小相等、方向相反，互相抵消，且上下端部磁環與中間磁環輔助增加了主磁鋼的磁場強度，為了簡化磁路分析，僅考慮主磁鋼的磁動勢對整個磁路的作用。圖3(b)為電機的等效磁路圖[12]，Fm1、Rm1分別為上主磁鋼的磁動勢和磁阻，Fm2、Rm2分別為下主磁鋼的磁動勢和磁阻，Rδ1、Rδ2分別為上氣隙磁阻和下氣隙磁阻；Rτ1、Rτ2分別為上氣隙邊緣磁阻和下氣隙邊緣磁阻，R1、R2分別為內外磁極的磁阻。

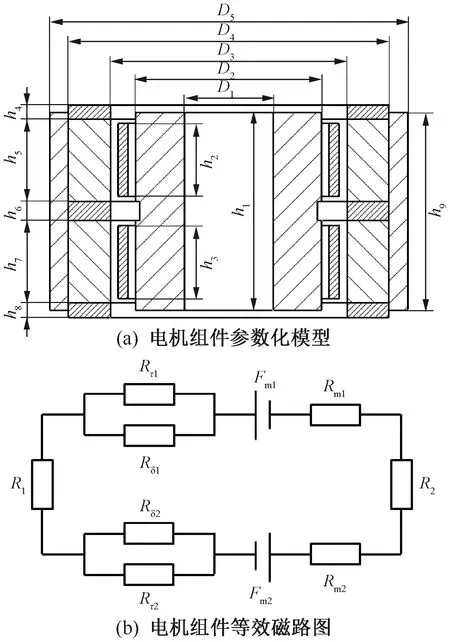
圖3 電機組件圖

磁路磁阻的計算公式如下：

R=h/(μA)

(1)

式中：h為磁阻單元的長度；μ為磁阻單元的絕對磁導率；A為磁阻單元的橫截面積。為了簡化計算，按內外磁極軸線方向計算磁阻，此時兩者的磁阻：

(2)

(3)

式中：μr1為內外磁極的磁導率；D1為內磁極內徑；D2為內磁極外徑；D4為磁鋼外徑；D5為外磁極外徑；h1為內磁極軸向厚度；h9為外磁極軸向厚度。當內外磁極無磁飽和現象時，其磁導率較高，磁阻較小，此時消耗的磁動勢集中于氣隙和永磁體上，兩者的形狀均為環形，扇環形磁阻單元的徑向磁路磁阻按下式計算：

Rr=ln(r2/r1)/(μlπ)

(4)

式中：r1為環形磁阻單元內圓半徑；r2為環形磁阻單元外圓半徑；l為磁阻單元的軸向長度。由于h5=h7，根據圖3(a)中的尺寸，結合式(4)可得永磁體和間隙磁阻如下：

Rm1=Rm2=ln(D4/D3)/(μ0μr2h5π)

(5)

Rδ1=Rδ2=ln(D3/D2)/(μ0h5π)

(6)

式中：D3為磁鋼內徑；h5為主磁鋼軸向厚度；μ0為真空磁導率；μr2為永磁體的相對磁導率，通常取μr2=1.05。考慮到磁感應線通過氣隙時會產生邊緣磁阻，即非垂直穿過線圈的磁感應線產生的磁阻，得邊緣磁阻[13]：

Rτ1=Rτ2=Rδ1/(τ-1)

(7)

根據本文的電機結構，取邊緣磁阻系數τ=1.2。上下永磁體產生的磁動勢:

Fm1=Fm2=HcB(D4-D3)/2

(8)

式中：HcB為磁感矯頑力。通過圖3(b)可知，磁路的總磁通:

φ=(Fm1+Fm2)/(R1+R2+Rm1+

Rm2+5Rδ1/6+5Rδ2/6)

(9)

假定軟磁材料的磁導率μr1不變，將與尺寸無關的正系數分別設置為K1、K2、K3，可得氣隙處的平均磁感應強度:

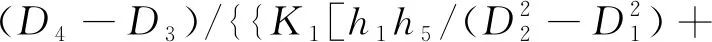
K3ln(D3/D2)}(D2+D3)}

(10)

式中,K1、K2、K3的表達式分別如下:

K1=1/(πHcBμr1)

(11)

K2=1/(2πHcBμr2μ0)

(12)

K3=5/(12πHcBμ0)

(13)

電機線圈受到的驅動力F=BIL，此時的電機效率：

η=(Fv)/(Fv+I2R)=

1/[1+ρI/(BvS)]

(14)

式中：ρ為電阻率;v為活塞運動速度;I為電流;S為線圈的橫截面積;B為氣隙磁感應強度。由式(14)可知，當壓縮機活塞直徑、繞線和氣體負載不變時，ρ、υ、S均不變，且電機效率與氣隙磁感應強度成正比，氣隙磁感應強度與主磁鋼內外徑、軸向長度、內外磁極內外徑、軸向長度、氣隙內外徑均相關。

1.2 雙動圈電機主要參數性能影響

依據上述等效磁路分析法，對有負載時壓縮機電機不同結構參數對電機性能的影響進行量化分析，圖4為有氣體負載時的壓縮活塞受力圖，其中Fe為電機的驅動力。

圖4 壓縮機活塞受力分析圖

基于Maxwell仿真平臺開展在熱力負載下壓縮機的電機仿真分析，以式(14)為基準對影響電機質量和電機效率的內磁極內外徑、外磁極內外徑、磁鋼內外徑進行精細化仿真，得到性質比最高的電機結構。以內磁極徑向厚度7.7 mm、磁鋼徑向厚度6.5 mm、外磁極徑向厚度3.0 mm的初始電機模型進行分析。

在初始模型上僅改變內磁極徑向厚度，其余部件的內外徑隨變，內磁極徑向厚度變化引起的電機質量和效率變化曲線如圖5所示。

圖5 內磁極徑向厚度對電機效率的影響

電機效率增速隨內磁極徑向厚度的增加先快后慢，根據式(10)，增加內磁極徑向厚度，即增加(D2-D1)/2，D4-D3不變，但分母減小，使氣隙磁感應強度B持續增大，通過式(14)可知，電機效率持續增大。但兩式默認軟磁材料的磁導率為定值，實際情況下，軟磁材料的磁導率隨著磁場強度的變化先大后小，且當通過軟磁材料的磁感應強度太大時會產生磁飽和現象，此時剩下的磁感應線不再進入軟磁材料。在該模型中，永磁體產生的磁動勢不變，限制了氣隙磁感應強度B的上限，增大內磁極厚度，僅緩解了磁飽和現象，所以電機效率的增速呈現先急后緩的趨勢變化，但電機質量隨著內磁極的增大而呈二次方關系增加。折中質量和效率，選定圖5中內磁極厚度為10 mm時對應的電機模型，此時電機效率為83.98%。

為了進一步提升效率，采用增加磁鋼徑向厚度,即增加(D4-D3)/2的方法增加磁路的磁動勢，如圖6所示。隨著磁鋼厚度的增加，式(10)中D4-D3的變化幅度遠大于K2ln(D4/D3)的變化幅度，氣隙磁感應強度B一直增大，電機效率隨之增加。電機效率增加趨勢先急后緩，這是因為磁鋼產生的磁動勢增加，通過內外磁極的磁通量變大，而內外磁極的徑向厚度不變，磁場越來越趨于飽和，使電機效率增速變緩。

圖6 磁鋼徑向厚度對電機效率的影響

選取磁鋼徑向厚度為8.8 mm時為最優，此時電機效率為86.72%。當內磁極與磁鋼徑向厚度分別為10 mm、8.8 mm時，改變外磁極徑向厚度，即改變(D5-D4)/2，電機效率和質量的變化曲線如圖7所示。

圖7 外磁極徑向厚度對電機效率的影響

2 直線電機顫振力特性研究

對于空間制冷機而言，除了考慮效率、質量兩個指標外，其自身引起的顫振也不能忽視[14]。制冷機的顫振會干擾空間探測器的測量精度和成象質量，從兩側電機的動力參數入手分析振動形成的具體原因，并與仿真分析相結合，提出控制壓縮機顫振的參數調整方法，從源頭減小制冷機的顫振量級。

2.1 一階顫振特性分析

雙活塞對置式壓縮機在生產過程中不可避免存在材料屬性偏差、零件尺寸偏差、質量偏差、充磁偏差等，使板簧剛度、動子質量、氣隙磁場強度均有偏差，兩側動子的慣性力F=m·a不同，導致壓縮機存在一階顫振力，ΔF=Δ(m·a)=m·Δa+Δm·a+Δm·Δa。針對上述設計的電機進行了模擬仿真，量化分析了板簧剛度、動子質量和氣隙磁場強度偏差對一階顫振力的影響。由圖8～圖10可知：同行程下兩側板簧剛度、磁鋼剩磁、動子質量偏差越大，一階顫振力越大；差異相同時，電機驅動力F的提升帶動活塞行程增大，一階顫振力隨著行程的增加而增加。

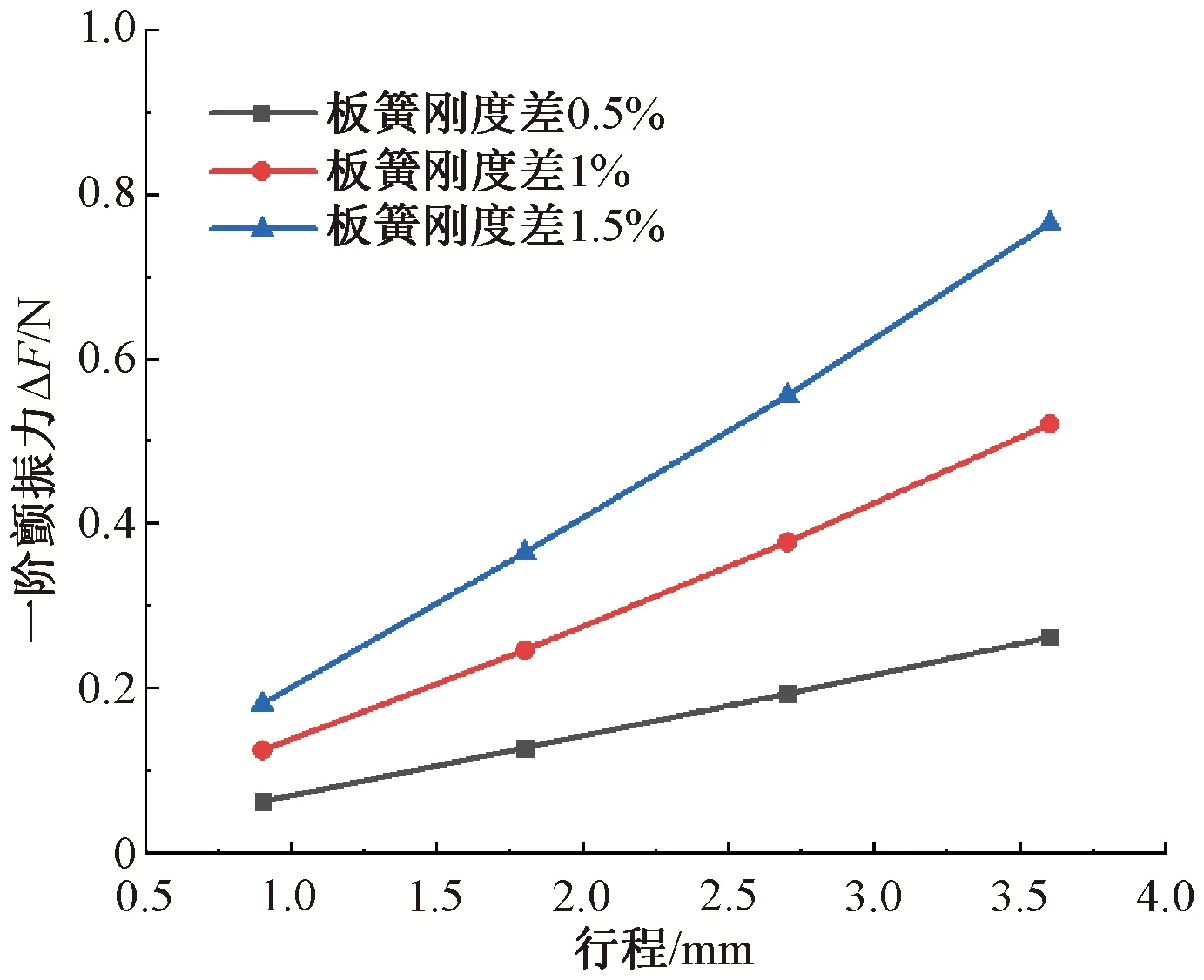
圖8 兩側板簧剛度差異產生的一階顫振力

圖9 兩側磁鋼剩磁差異產生的一階顫振力

圖10 兩側質量差異產生的一階顫振力

實測壓縮機A、B兩側動力參數如表2所示，動力參數差異使達到同活塞行程時兩側動子的一階軸向力不同，此時壓縮機就會產生一階顫振力。

表2 電機兩側各參數狀態

仿真發現，同行程下B側產生的動能大于A側，結合圖8～圖10，通過改變壓縮機A側動子質量,可使兩側動子的運動動能一致，將壓縮機一階顫振力降至較低水平。依據表2的參數狀態，模擬分析了在A側增加動子質量時的一階顫振力輸出情況，如圖11所示。

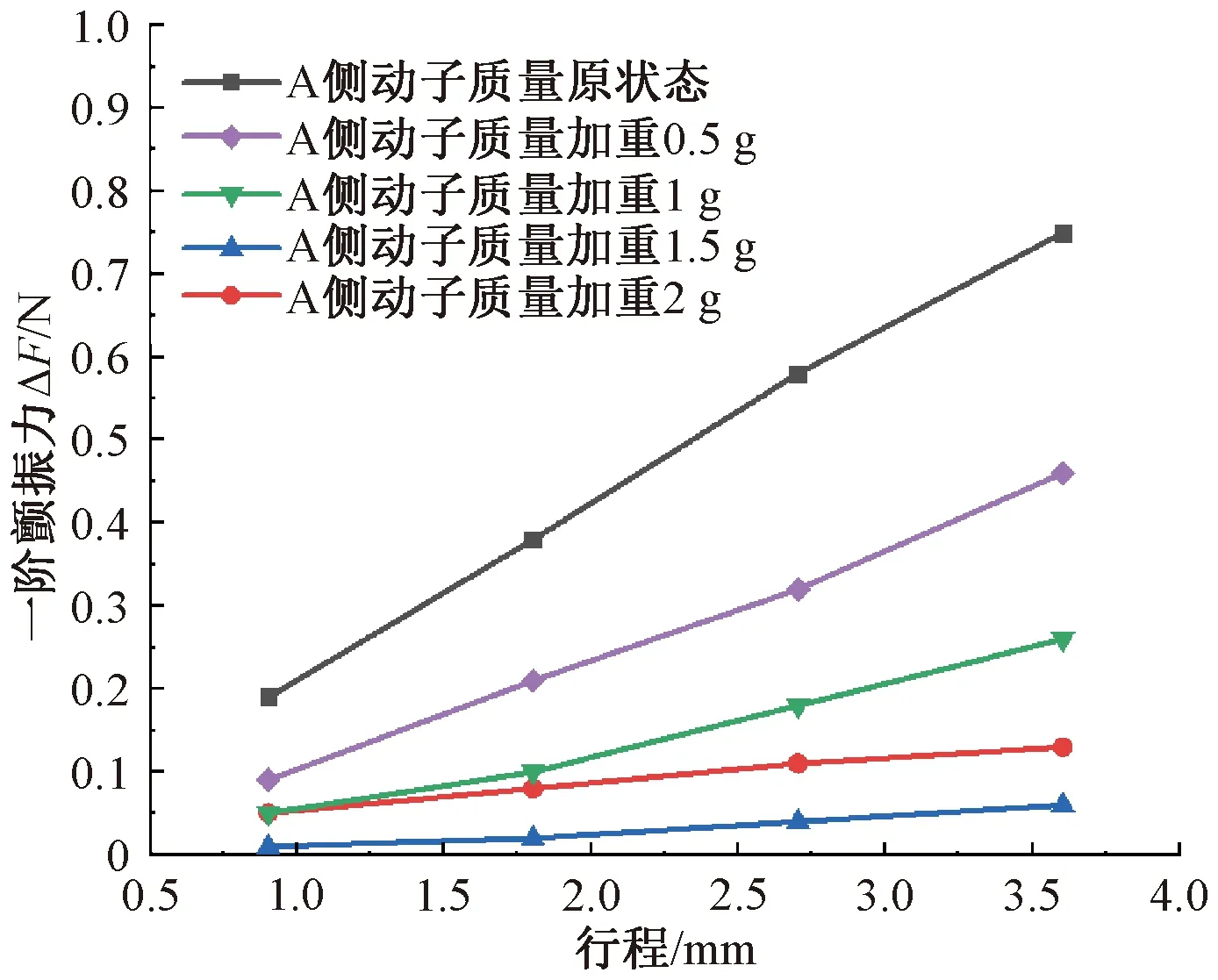
圖11 一階顫振的仿真結果

2.2 二階顫振特性分析

直線電機運行過程中，線圈產生的感應電動勢形成的交變磁場存在二階分量，使壓縮機產生二階顫振。在一些對振動敏感的場合，二階顫振不能被忽視。本文對二階顫振產生的原因及其具體數值進行定量化研究，為消除二階顫振提供理論支持和數據支撐。Halbach陣列采用了雙動圈電機，由于單個線圈穿越兩個方向相反的磁場，故動子線圈在不同位置處電機的比推力BL變化劇烈，如圖12所示。

圖12 雙動圈比推力隨軸向位置的變化曲線仿真

在實際裝配中，壓縮機兩側的位置偏差很小，即在兩側電機的差異落在圖12上一小段較小的行程范圍內，將該小段視為線性變化，此時比推力大小與位移的關系：

BL=kx+b

(15)

式中：k，b為與位移無關的系數；x為位移。電機總推力：

F=BLI=[kxmaxsin(ωt)+b]·

Imaxsin(ωt+φ)

(16)

式中：xmax為位移幅值；Imax為電流幅值；ω為角速度；φ為電流與位移的相位。將式(16)轉化：

F=bImaxsin(ωt+φ)-kxmax·

Imax[cos(2ωt+φ)-cosφ]/2

(17)

由式(17)可知，推力出現了二階分量，若兩側動子相對靜子組件的軸向位移不一致，則同時刻兩側動子的位移不一致，產生的二階顫振力也不相同，即衍生出壓縮機的二階振動。圖13為電機一側動子軸向平衡位置發生偏移，另一側動子軸向平衡位置處于理論中心位置時的二階顫振力仿真。根據二階顫振仿真結果，隨著偏置的增大、活塞位移的增加，二階顫振力顯著增加。

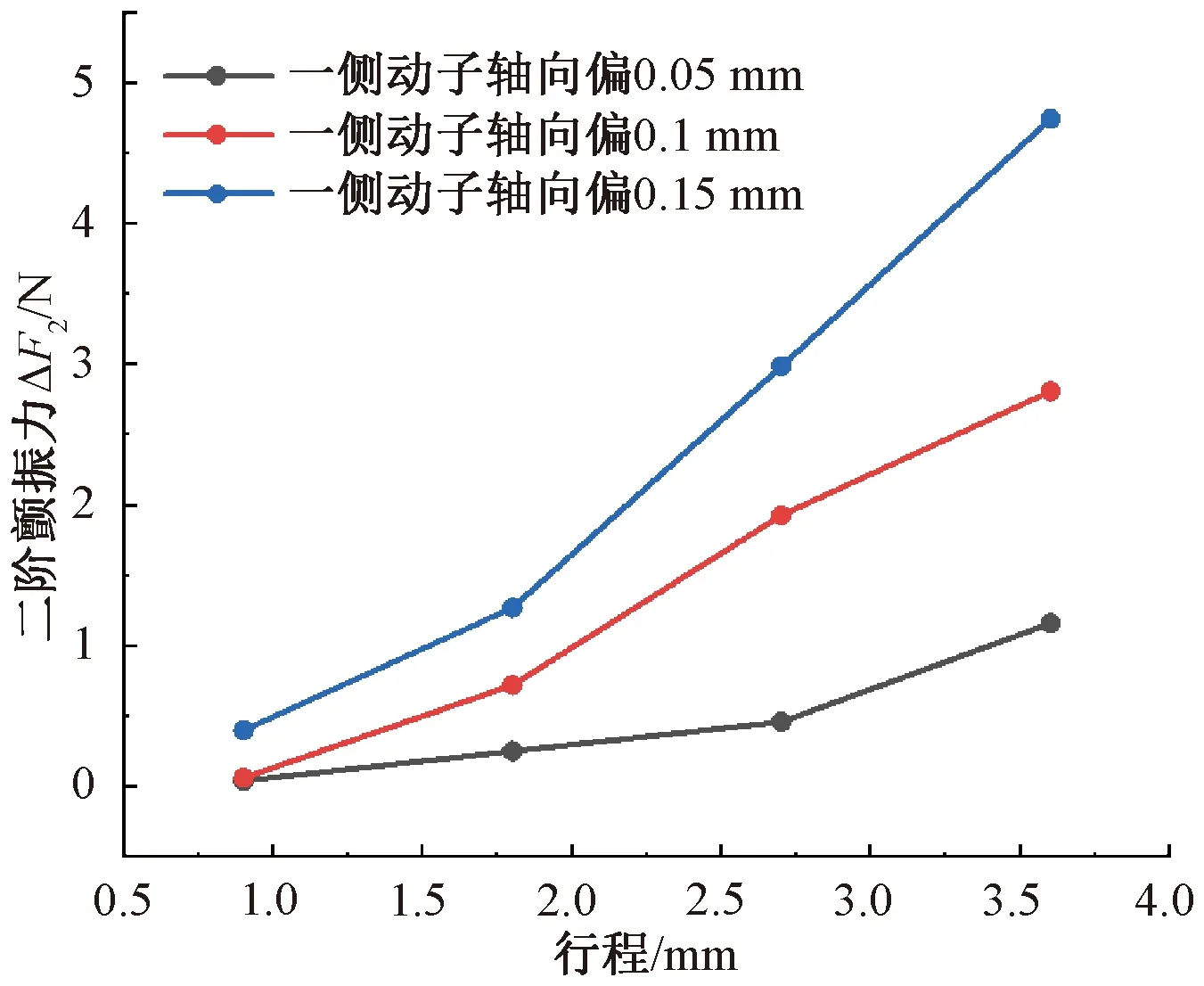
圖13 電機動子不同軸向偏置和不同位移下的二階顫振力仿真

3 實驗研究

3.1 耦合冷指的壓縮機電機性能測試

根據上述分析，研制了質量僅為4.5 kg的壓縮機，其單側電機質量為1.141 kg、外形尺寸為φ73.4 mm×43 mm，并將壓縮機連接70 K冷指進行了相關實驗驗證。

圖14 壓縮機性能測試實驗圖

電機組件中內外磁極材料使用高磁導率的DT4E，其飽和磁感應強度達到2.4 T；線圈使用0.6 mm的漆包線，耐用電流為4.5 A；Halbach陣列磁鋼材料均為N50H。制冷機達到6 W@70 K制冷量時壓縮機的電參數如表3所示。

表3 6 W@70 K制冷量壓縮機電參數

圖15是壓縮機連接冷指的性能測試實驗結果，其中功耗為壓縮機的輸入電功，實測效率與有限元仿真下的電機效率非常接近。該方法可行性較強，具備一定的指導意義。

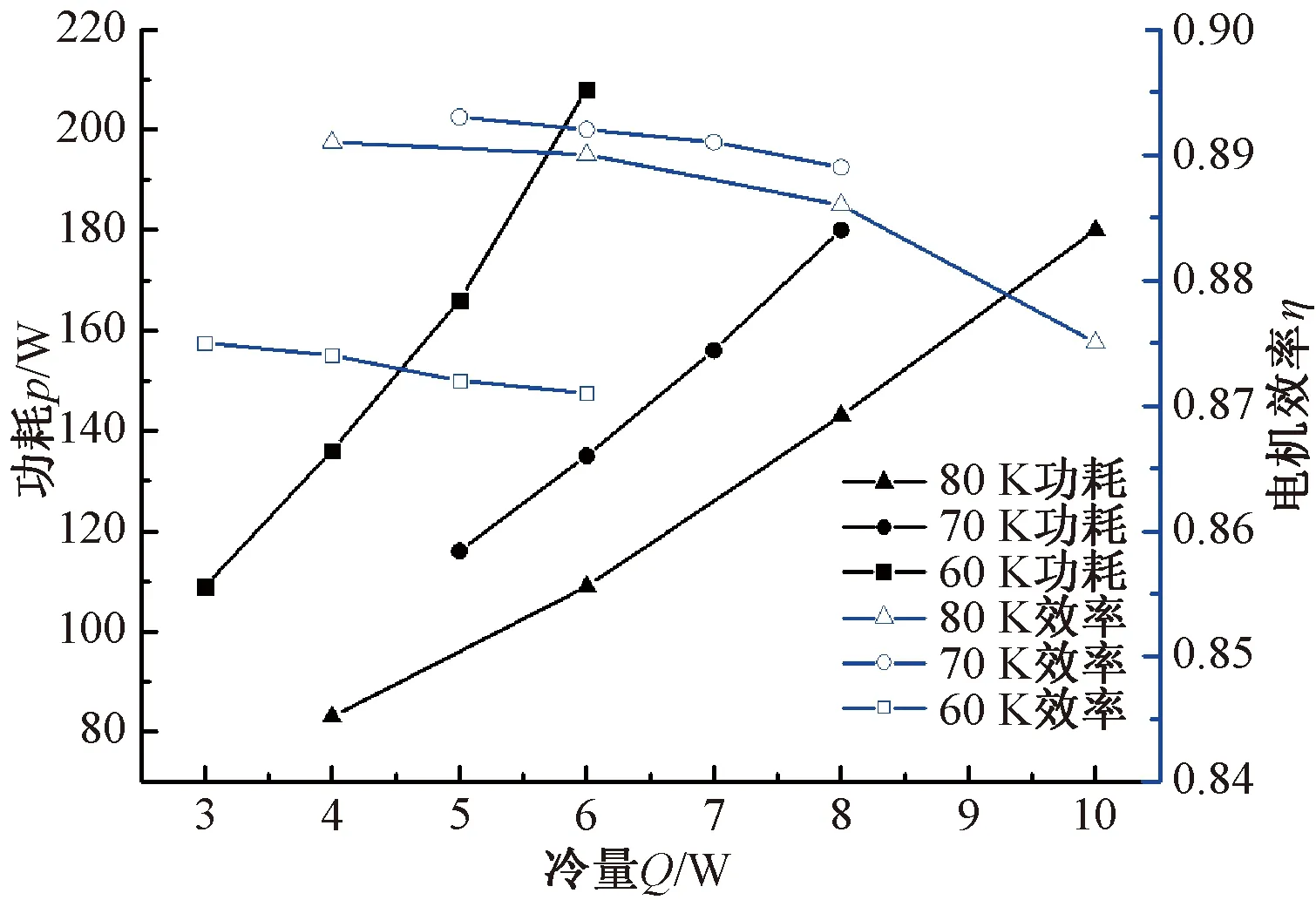
圖15 制冷機制冷性能曲線圖

3.2 電機顫振力特性測試

為了驗證控制壓縮機顫振力方法的有效性，搭建壓縮機顫振測試平臺，將壓縮機與冷指耦合連接在顫振力測試平臺上，通過測量軸線方向加速度值來計算壓縮機的軸向顫振[15-16]。圖16是動圈式壓縮機改變A側動子質量后的顫振力實測值和仿真值。可以看到，當A側動子質量增加1 g時，一階顫振明顯減小，當A側動子質量增加2 g時，相對于前者一階顫振反而會增大，表明適當增加一側動子質量對削弱一階顫振有積極作用。調整A側動子質量對壓縮機軸向一階顫振力的改善非常明顯，±3.6 mm行程時，一階顫振輸出由原0.75 N消弱至0.25 N，衰減幅度達66.7%。

圖16 實測壓縮機軸向一階顫振力

實驗測試了壓縮機樣機的二階顫振力，如圖17所示。原狀態二階實測顫振力與圖13中軸向偏移0.1 mm仿真值較為接近，這與實際裝配過程中，每側動子組件相對于靜子組件軸向平衡位置的偏差在0.05 mm內，兩側動子軸向偏移絕對值在0.1 mm以內的實際工藝控制水平相符。基于上述電機平衡位置偏差對壓縮機二階顫振力的規律模擬分析，工藝上采用調整一側電機的軸向平衡位置實現二階顫振力的消減。由圖17可以看出，A側墊高0.05 mm后壓縮機二階顫振力有了大幅降低，二階顫振力從2.3 N降低到0.5 N，衰減幅度達78.3 %，說明該方法起到了顯著的減振效果。

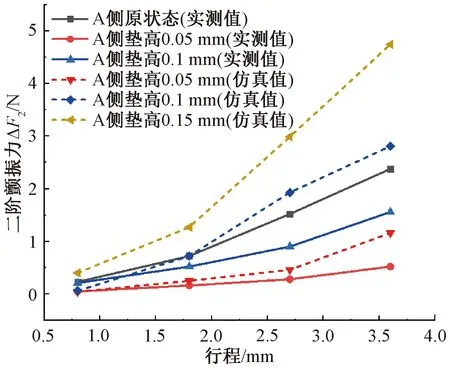
圖17 實測壓縮機軸向二階顫振力

4 結 語

本文建立了動圈式電機的等效磁路模型，分析了動圈式直線電機各部件尺寸參數對磁路和電機效率的影響，設計出一款質量小、推力大、電機效率高的動圈式線性壓縮機。從電機本體入手分析了壓縮機多階顫振形成的具體原因，與有限元仿真分析相結合，量化壓縮機兩側動子不同狀態對一階和二階顫振力的影響，并提出控制壓縮機顫振的方法。將線性壓縮機與冷指進行耦合實驗，性能測試結果驗證了壓縮機中電機設計方法的準確性，變參數顫振力測試結果驗證了控制壓縮機顫振方法的有效性。