一種雙裕度旋轉變壓器的優化設計及仿真分析
王永博,李長年,許興斗,周奇慧,周競捷
(中國電子科技集團公司第二十一研究所,上海 200233)
0 引 言
旋轉變壓器作為角度傳感器,具有精度高、可靠性高、環境適應性強等特點,廣泛應用于軍工、航空、航天、汽車等場合[1]。雙裕度旋轉變壓器將兩套旋轉變壓器集合為一體,兩套旋轉變壓器均可以獨立工作,進一步提高了整個產品的可靠性。
在某些特殊場合下,雙裕度旋轉變壓器中的兩套旋轉變壓器需要同時工作,分別與兩套上位機系統進行交互,并同時將機構的旋轉角度進行輸出。
本文針對某一種雙裕度旋轉變壓器(以下簡稱旋變)進行研究,該雙裕度旋變由兩套無刷旋變組成并同時工作,應用場路耦合的方法對其結構尺寸及結構布局進行優化,并完成實驗驗證。
1 工作原理
雙裕度旋變的結構圖如圖1所示,內部兩套旋變均為無刷結構,無刷旋變A和無刷旋變B集合為一體。無刷旋變A組成部分包括:旋變A定子、旋變A轉子、環變A定子和環變A轉子;無刷旋變B組成部分包括:旋變B定子、旋變B轉子、環變B定子和環變B轉子。
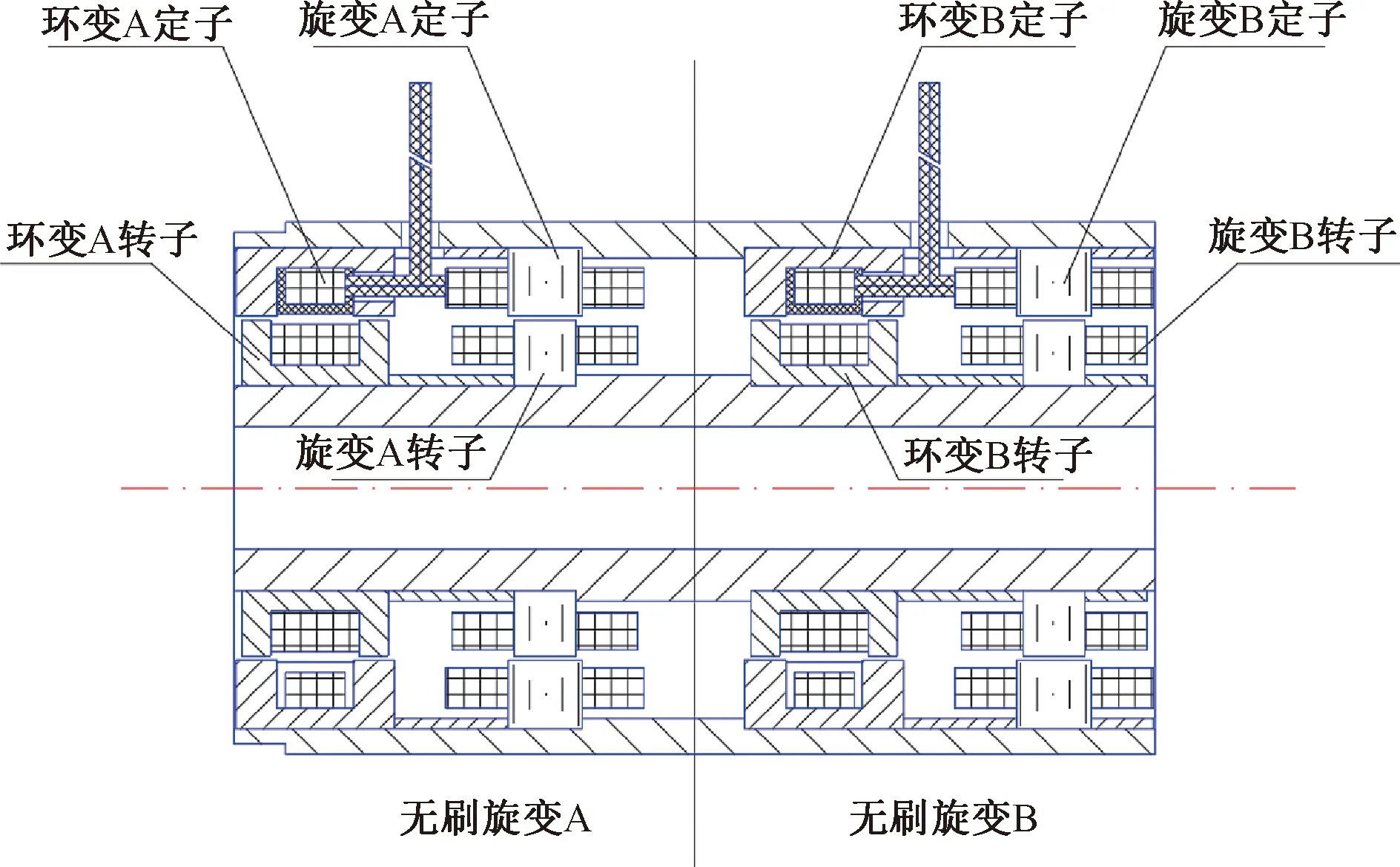
圖1 雙裕度旋變結構圖
無刷旋變A和無刷旋變B的工作原理相同,以無刷旋變A為例說明。環變A定子繞組激磁,通過電磁感應在環變A轉子繞組中生成電信號,環變A轉子繞組通過短接將電信號傳遞給旋變A轉子繞組,再通過電磁感應在旋變A定子繞組中產生兩路正交的電信號,兩路信號與轉子轉角成正余弦關系,分別為正弦輸出信號和余弦輸出信號。將兩路信號進行處理即可以得到轉子轉角,用來指示轉角位置[2]。
雙裕度旋變的電壓方程式如下。
無刷旋變A:
UA_EXC=Usin(ωt)
UA_SIN=KUsin(ωt)sinθ
UA_COS=KUsin(ωt)cosθ
無刷旋變B:
UB_EXC=Usin(ωt)
UB_SIN=KUsin(ωt)sinθ
UB_COS=KUsin(ωt)cosθ
式中:兩套無刷旋變以下標A和B區分,UEXC表示激磁電壓,USIN表示正弦輸出電壓,UCOS表示余弦輸出電壓;U為激磁電壓有效值;K為變壓比;ω為激磁頻率;θ為轉子轉角。
雙裕度旋變電氣原理圖如圖2所示。
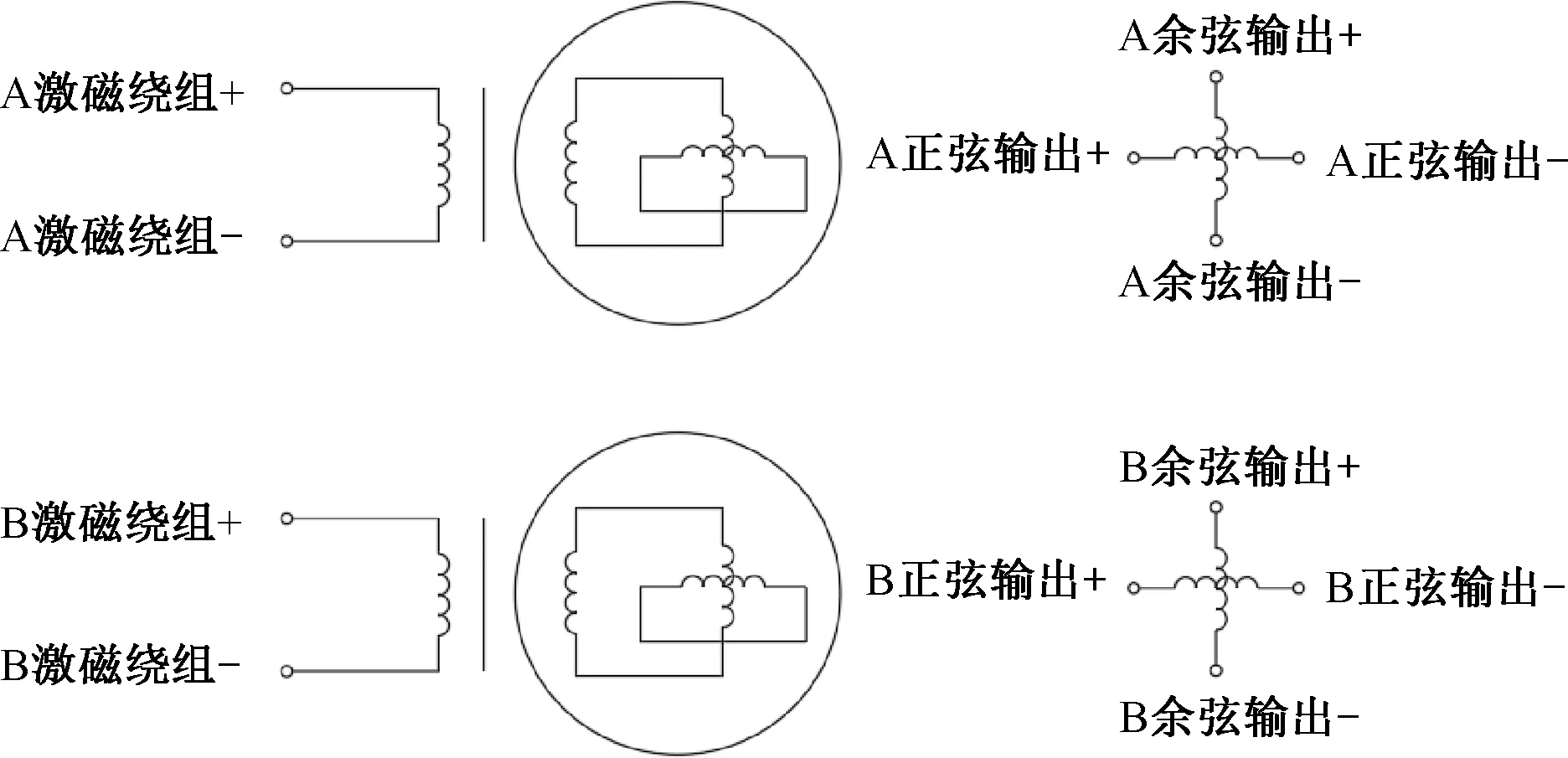
圖2 雙裕度旋變電氣原理圖
2 磁路法確定初步方案
通過磁路法將磁路等效成磁阻,可將求解磁場問題簡化成求解磁路的問題,快速計算出電磁方案。雙裕度旋變中的兩套無刷旋變電磁方案相同,結構設計相同。
無刷旋變磁路法的求解過程:以主要技術指標作為目標參數,以尺寸參數和繞組參數作為計算輸入,結合公式及磁化曲線、損耗曲線查表,完成磁路、損耗的計算與迭代,使飽和系數和電勢系數誤差最小,最后再校核計算輸出是否滿足主要技術指標[3]。
計算流程圖如圖3所示。
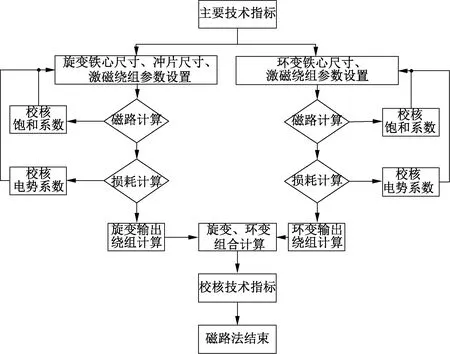
圖3 磁路法計算流程
用在特殊場合的此種雙裕度旋變,安裝后會存在±0.3 mm的軸向竄動量,為滿足實際使用要求,旋變定子鐵心厚度和環變鐵心齒厚度應預留0.6 mm的余量。通過磁路法計算,各鐵心尺寸主要設計參數如表1所示。
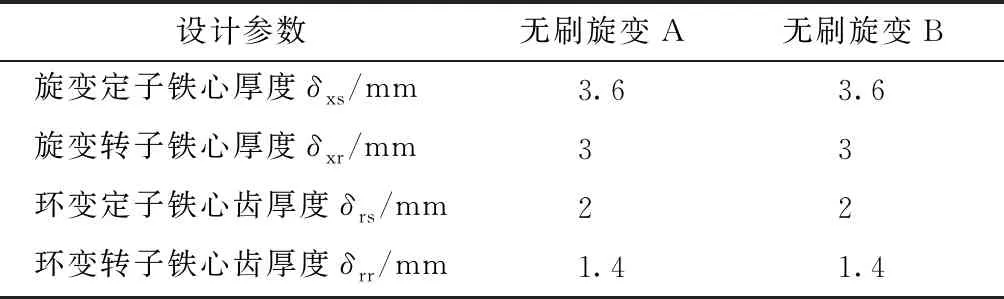
表1 初步設計參數
3 有限元優化設計
磁路法無法準確模擬真實的磁場,在對雙裕度旋變軸向尺寸優化時,無法準確反映優化前后的差異。另外,此種雙裕度旋變的工作模式較為特殊,兩套無刷旋變需要同時工作,在此情況下,兩套無刷旋變的磁場將會相互影響,傳統的磁路法已無法求解這種磁場。
為了解決以上問題,可以采用有限元法對電磁場計算,將求解場的微分問題轉換為各剖分網格下泛函求極值的問題,更為準確地計算出電磁場。本文采用有限元仿真軟件Maxwell對雙裕度旋變完成兩方面的優化:軸向尺寸的優化設計;兩套無刷旋變的合理布局。
3.1 軸向尺寸的優化
將環變定子側激磁作為原方,環變轉子側感應電信號作為副方。圖1中,環變鐵心內部中間為環形槽,其中放置線圈;兩側的軸向鐵心部分為環變的齒部,主要起導磁作用。
在對軸向尺寸進行優化時,應保證雙裕度旋變仍滿足在軸向竄動中使用的要求。圖4為軸向尺寸優化前后的對比。圖4中,優化前為磁路法計算出的方案,L為無刷旋變的軸向長度,軸向尺寸X等于軸向竄動量(±0.3 mm)。
軸向尺寸的優化方法為環變原(副)方兩側齒部厚度不等,而初步方案中原(副)方兩側齒部厚度是相等的。
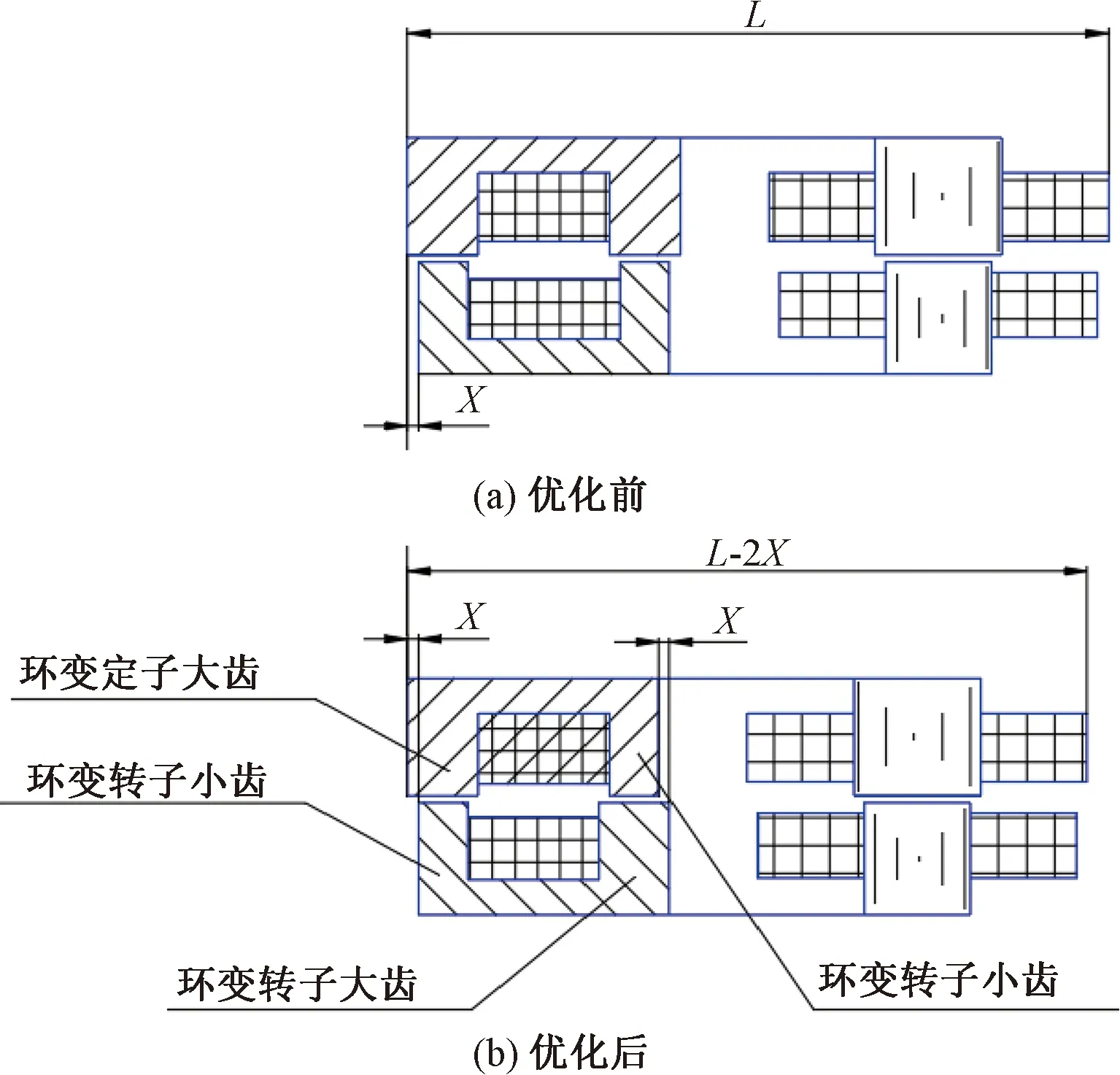
圖4 優化前后軸向長度對比
圖4中,優化后的環變定子鐵心兩側齒部厚度不等,軸向長度相差2X;環變轉子鐵心兩側齒部厚度也不等,軸向長度也相差2X。環變定子的大齒對應環變轉子的小齒,環變定子的小齒對應環變轉子的大齒。這種環變原(副)方兩側齒部厚度不等的結構使得單個無刷旋變軸向長度為L-2X,軸向長度減小2X,雙裕度旋變將減小軸向長度4X。
環變原(副)方兩側齒部厚度不等,則環變磁場將不再對稱。下面應用有限元法計算采用該結構是否仍能滿足性能要求。
優化前和優化后的磁力線圖如圖5所示。從圖5中可以看出,磁路主要路徑均為環變定子齒和轉子齒,優化前有一部分漏磁路不經過環變轉子齒,由于匝鏈環變轉子繞組的磁鏈減少,故優化前的感應電動勢將比優化后的感應電動勢稍小一些。
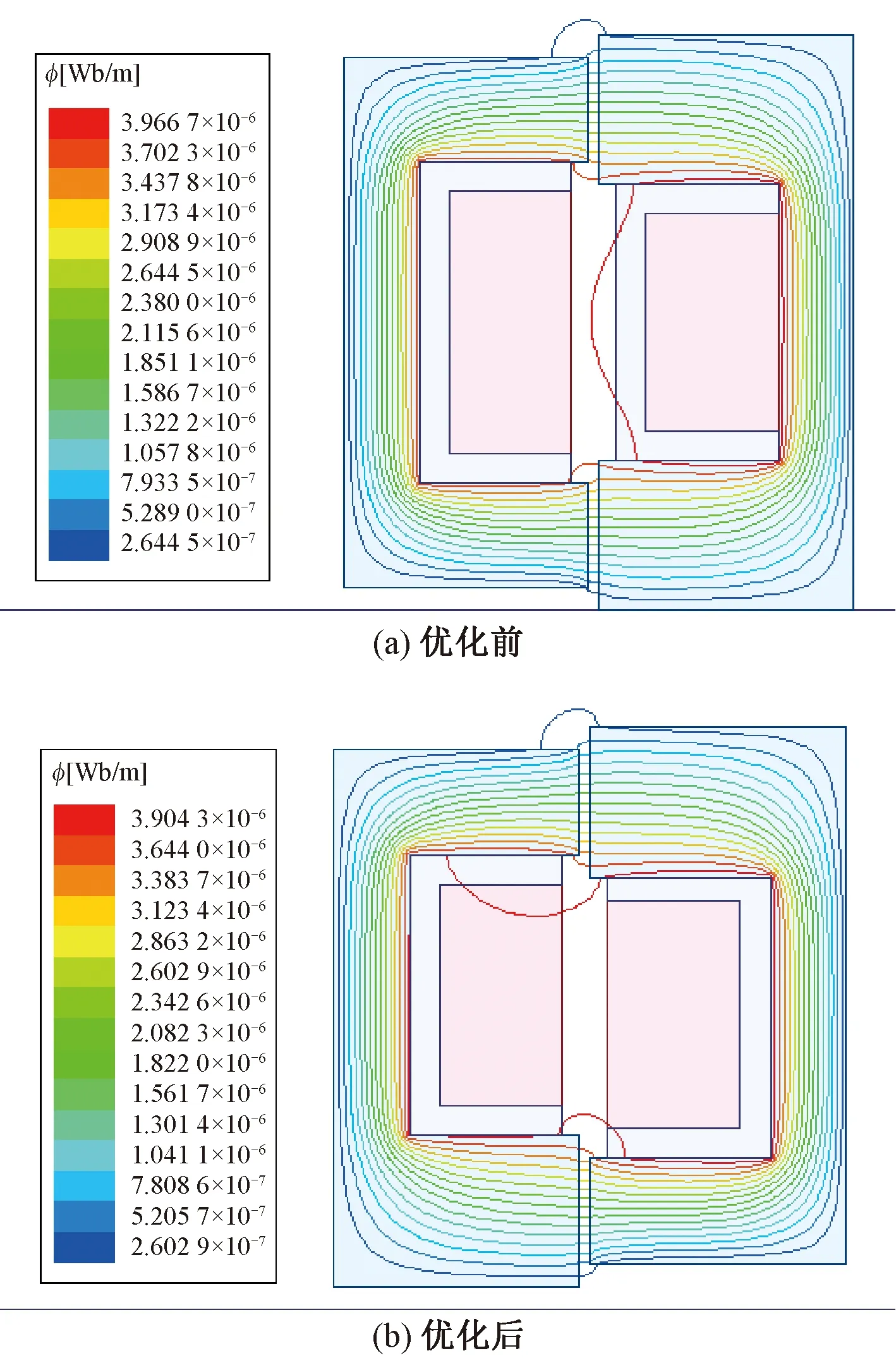
圖5 優化前后磁力線圖
優化前和優化后的磁密云圖如圖6所示。優化前后鐵心中各部位磁密飽和程度基本一致。
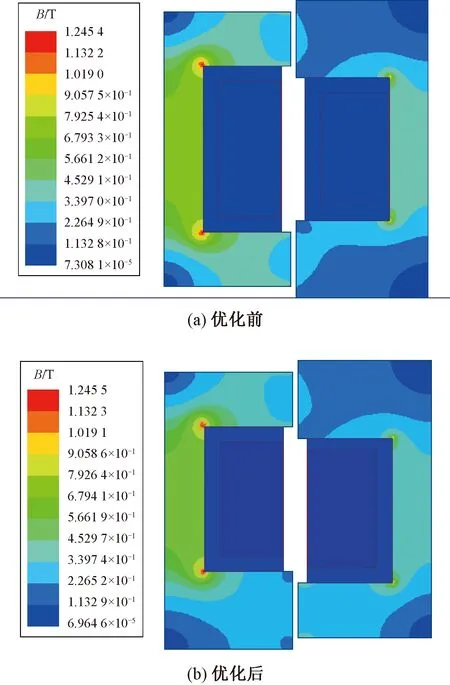
圖6 優化前后磁密云圖
計算優化前后環變的輸出電壓,如表2所示。從表2中可知,在不同位置的輸出電壓變化率優化后高于優化前,但變化率僅為0.35%,遠小于實際使用中小于等于10%的要求。
由以上有限元計算結果可知,環變原(副)方兩側齒部厚度不等的結構(即優化方案)可以減少雙裕度旋變的軸向長度,而對于環變的輸出電壓則沒有影響。
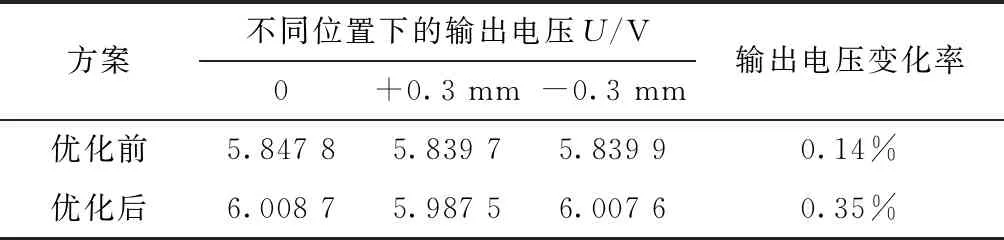
表2 優化前后輸出電壓對比
3.2 內部布局的優選
3.2.1 兩種布局的對比
雙裕度旋變中兩套無刷旋變同時工作,兩套無刷旋變產生的磁場將會相互影響,這種影響會反映到無刷旋變的輸出角度中。雙裕度旋變按照環變與旋變的相對位置關系,可分為非對稱排布和對稱排布,即兩種布局方式:環變A—旋變A—環變B—旋變B(第一種布局),旋變A—環變A—環變B—旋變B(第二種布局),兩種布局如圖7所示。
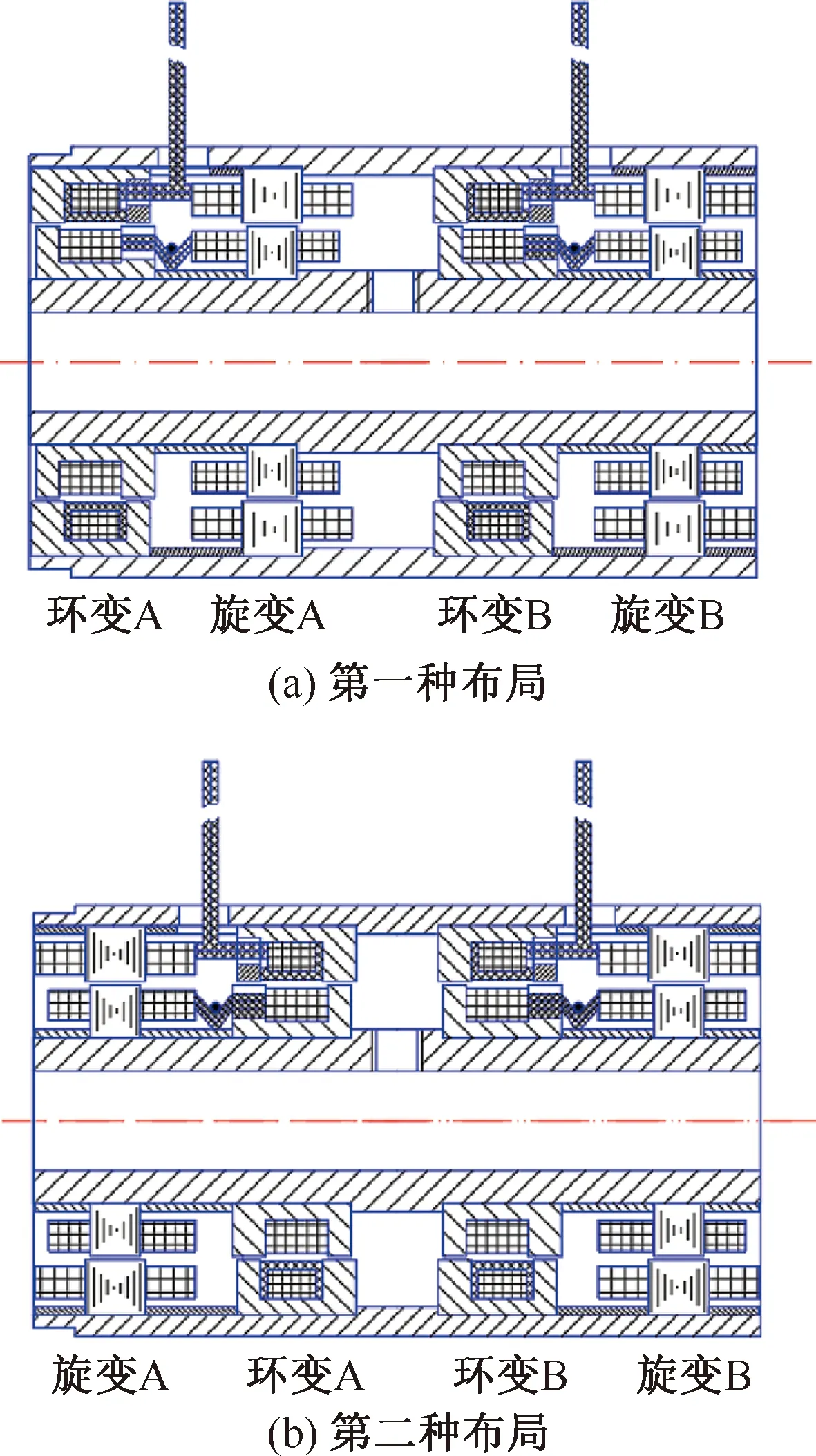
圖7 兩種布局方式
應用有限元法計算兩種布局方式下,兩套無刷旋變各自在不同轉子位置下的正弦輸出電壓和余弦輸出電壓,再經過解算算法計算,可以求得兩套無刷旋變各自的解算角度。通過對比可知,兩套無刷旋變同時工作時,相互作用的磁場對兩種布局的影響程度是不同的,影響較小的一種布局方式更合理。
求解無刷旋變解算角度的計算框圖如圖8所示。

圖8 解算角度計算框圖
兩種布局方式分別建立三維模型,(如圖9、圖10所示),應用有限元仿真軟件計算兩套無刷旋變同時工作,轉子在不同位置下的正弦及余弦輸出電壓,并通過解算算法計算出無刷旋變輸出角度。
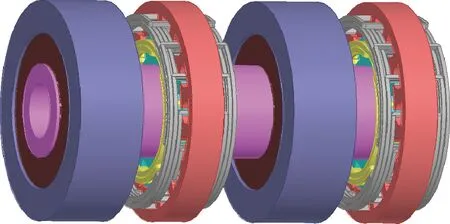
圖9 第一種布局(隱藏機殼)
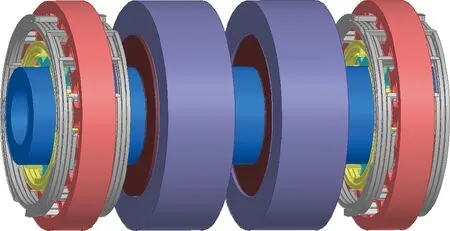
圖10 第二種布局(隱藏機殼)
第一種布局下,無刷旋變A和無刷旋變B同時工作時,選取轉子6個位置(0°、30°、60°、90°、180°和270°),計算無刷旋變A的正余弦輸出電壓和無刷旋變B的正余弦輸出電壓,并將計算結果進行解算,得到無刷旋變A和無刷旋變B同時工作時轉子在各個位置下輸出角度值。
實際應用中,無刷旋變A和無刷旋變B將輸出角度分別傳輸給兩套上位機系統,兩者的角度偏差越小,兩套系統接收到的轉角位置越一致,后續機構執行動作越準確。
第一種布局下,無刷旋變A和無刷旋變B在各位置下輸出角度值及角度偏差,如表3所示。
第二種布局下,無刷旋變A和無刷旋變B同時工作時,選取轉子相同的6個位置,計算無刷旋變A的正余弦輸出電壓和無刷旋變B的正余弦輸出電壓,并將計算結果進行解算,得到無刷旋變A和無刷旋變B同時工作時,轉子在各個位置下輸出角度值及角度偏差,如表4所示。
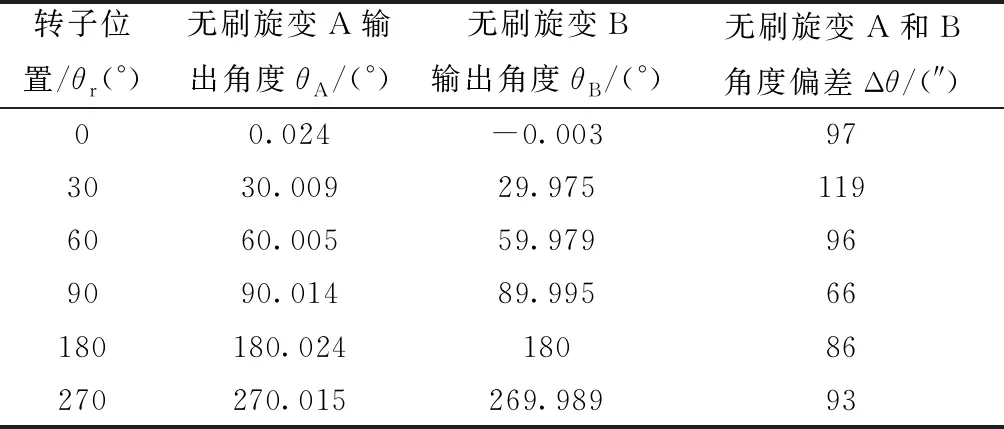
表3 第一種布局下角度偏差
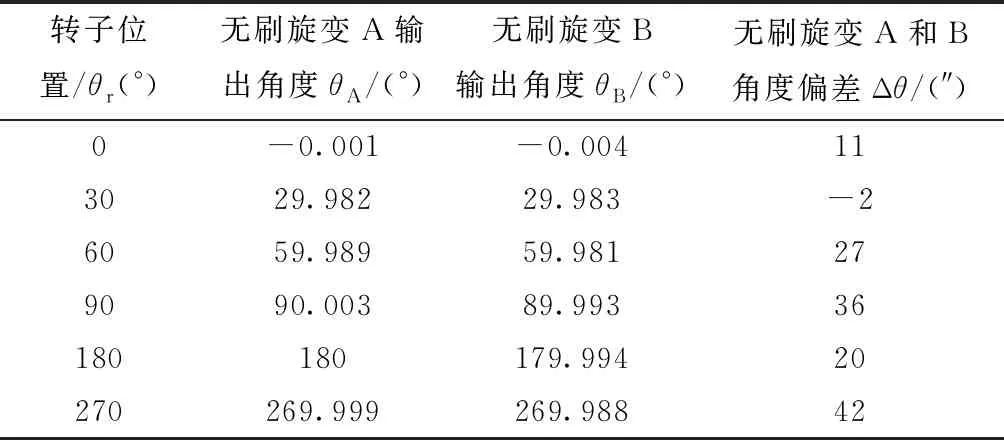
表4 第二種布局下角度偏差
通過表3和表4對比兩種布局下無刷旋變A和無刷旋變B的角度偏差,第二種布局角度偏差最大為36″,而第一種布局角度偏差最大為119″,第二種布局下的角度偏差明顯較小,說明第二種布局下兩套無刷旋變的相互影響較小,第二種布局更為合理。
由無刷旋變輸出角度進一步計算,可以求得無刷旋變在該位置的誤差值。兩種布局下,無刷旋變A和無刷旋變B在各個位置下的誤差值如表5、表6所示。
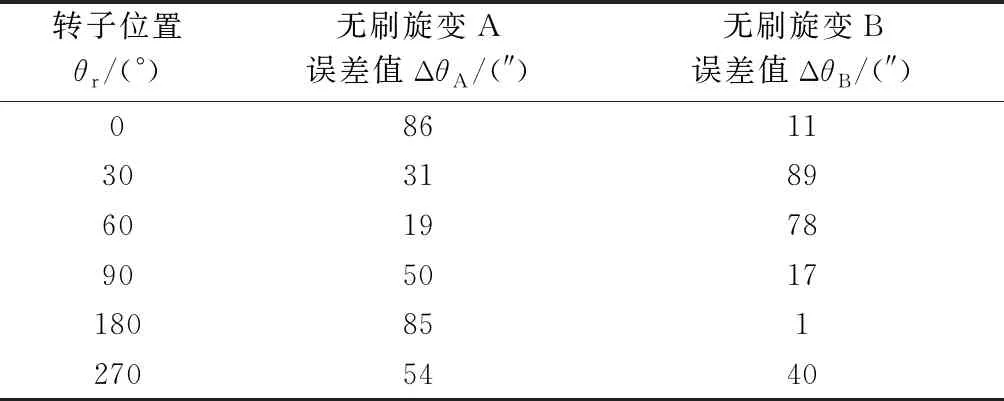
表5 第一種布局下的角度偏差

表6 第二種布局下的角度偏差
對比表5和表6,無刷旋變A在第二種布局下的最大誤差值65″小于第一種布局下的86″;無刷旋變B在第二種布局下的最大誤差值69″小于第一種布局下的89″,即第二種布局下無刷旋變A和無刷旋變B的誤差值均變小,說明兩套無刷旋變的相互影響較小,同樣表明第二種布局是更為合理的。
3.2.2 優選布局的電磁場計算
計算第二種布局下雙裕度旋變的磁密云圖如圖11所示,磁密矢量圖如圖12所示。從圖11、圖12中可以看出,由于無刷旋變的激磁方為環變定子,環變齒較窄,環變中磁密較高。第二種布局方式將旋變布置在雙裕度旋變的兩端,旋變A受到環變B的影響減弱,旋變B受到環變A的影響也減弱,因此兩套無刷旋變的角度偏差較小。
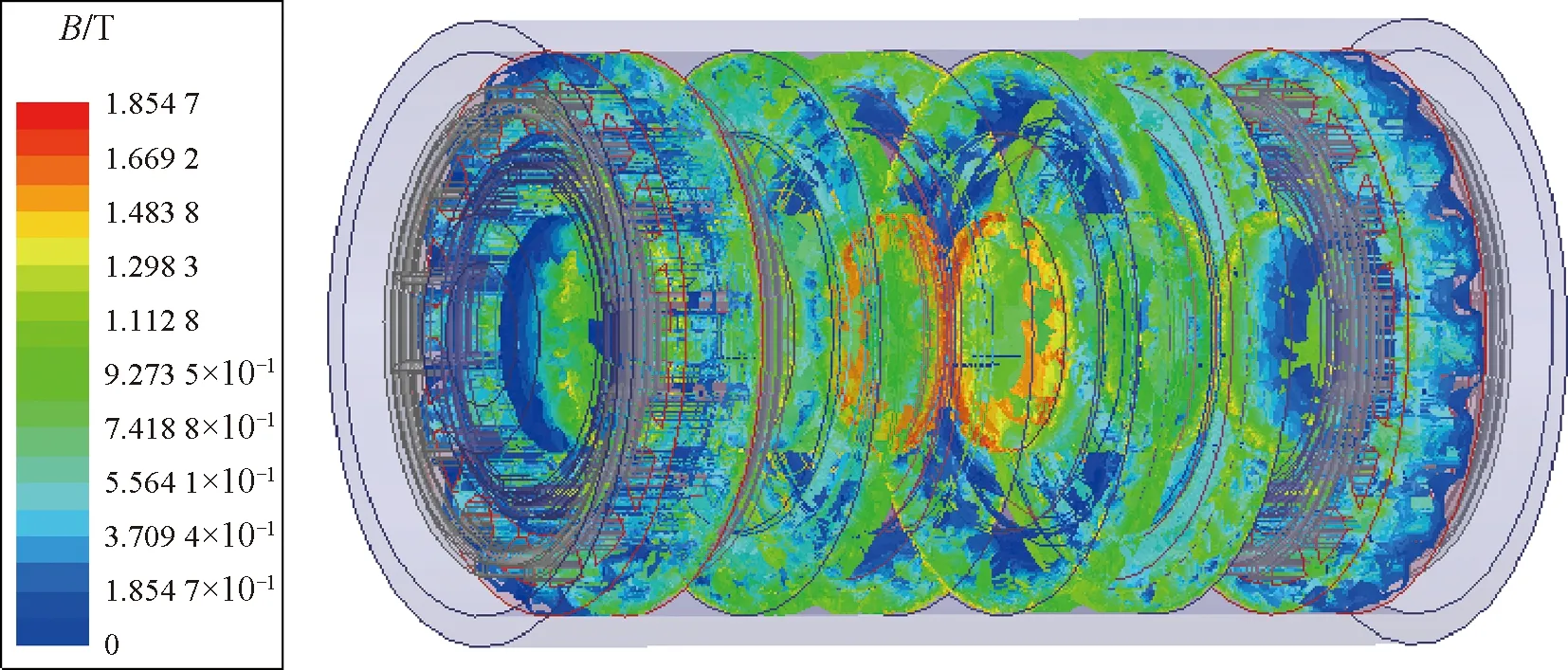
圖11 磁密云圖

圖12 磁密矢量圖
雙裕度旋變轉子轉動一周,第二種布局方式下無刷旋變A和無刷旋變B的輸出電壓波形如圖13所示。

圖13 雙裕度旋變輸出電壓
4 實驗驗證
按照以上分析及計算,確定雙裕度旋變的設計方案并生產樣機,主要設計參數如表7所示,樣機實物圖如圖14所示。
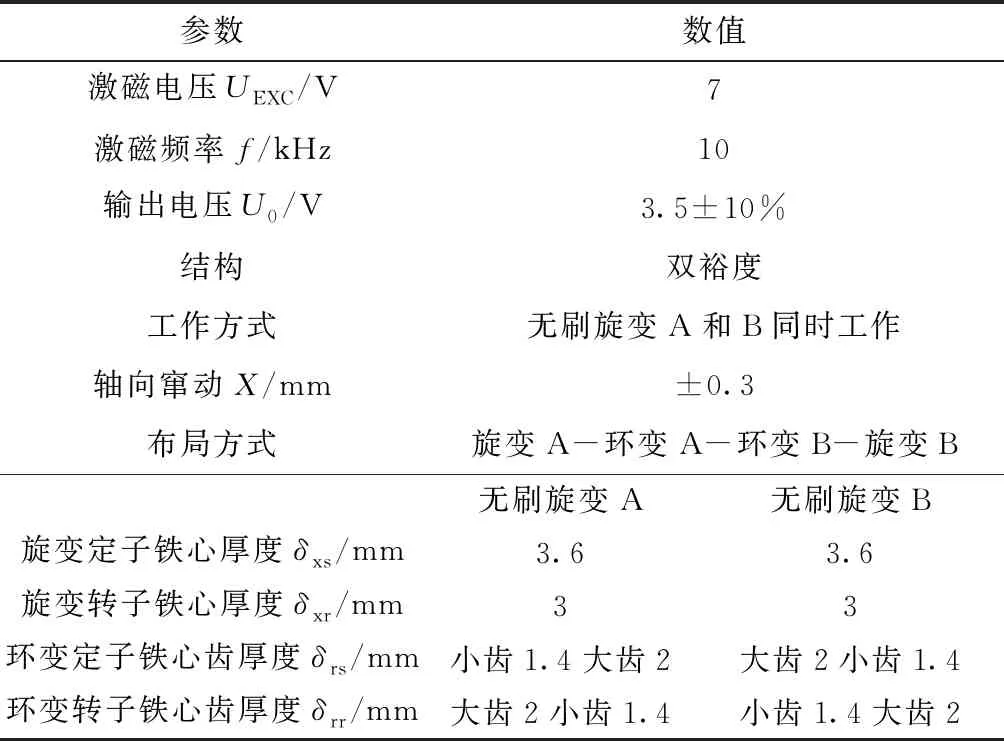
表7 樣機方案

圖14 樣機實物圖
樣機在各竄動位置下的輸出電壓和輸出電壓變化率如表8所示。測試結果均滿足要求,證明本文的仿真分析方法是可行的。

表8 樣機各竄動位置輸出電壓
樣機轉子在不同位置下兩套無刷旋變同時工作時的輸出角度偏差如表9所示。角度偏差最大為32″,滿足實際使用要求。該角度偏差反映了無刷旋變A和B磁場的相互影響程度,實驗測試結果與仿真計算結果為同一數量級,可以證明本文的仿真分析方法是可行的。

表9 樣機各位置下輸出角度偏差
5 結 語
在特殊應用場合,雙裕度旋變在軸向竄動下使用,以及內部兩套無刷旋變同時工作的使用需求。本文通過磁路法確定雙裕度旋變的初步設計方案,再結合有限元仿真方法,確定雙裕度旋變的優化方案,并以優化方案生產樣機進行驗證。本文的分析方法及設計思路,對類似產品的設計及優化具有參考價值。

