一種抑制齒槽轉矩的高精度定位伺服控制方法

高 鵬，尹 強，孫 樂，姜澤超，劉國棟

(1.南京理工大學 機械工程學院，南京 210094；2.南京理工大學 自動化學院，南京 210014；3.北方自動控制技術研究所，太原 030006)

0 引 言

永磁同步電機因其固有的結構特點，不可避免地會產生齒槽轉矩，從而引起振動與噪聲，國內外學者對此提出多種優化和改進措施。結合近年來國內外的研究成果，本文從結構優化方面對齒槽轉矩的抑制方法分類歸納，系統闡述了齒槽轉矩的影響因素，分析了各類方法的優缺點[1]。

與其他因素相比，低速時的齒槽轉矩是影響驅動性能的主要因素，甚至會引起速度振蕩。文獻[2]受齒槽轉矩特性的啟發，基于永磁同步電機模型提出了一種虛擬齒槽轉矩控制方法，減小了直接驅動永磁同步電機伺服系統在低速條件下的速度脈動。文獻[3]提出了一種基于瞬時轉矩估計、具有可解釋空間諧波的嚴格分析模型。該模型可以根據簡單的先驗知識和一些可測量的在線信息準確估計產生的扭矩，從扭矩估計中獲得的疊加電流可以消除脈動扭矩。

為抑制轉矩脈動，文獻[4]在q軸參考電流中加入一系列特定的諧波電流，產生額外的轉矩分量來抵消齒槽轉矩的基波和二階諧波分量，而不是對電機本身進行常規優化,該方法有效地抑制了轉矩脈動。為了減少轉矩脈動，文獻[5]提出了一種脈沖合并方法，該方法比傳統方法多采樣一個參考值，以改進電流控制，并將其應用于高速區域的齒槽轉矩抑制，具有明顯的效果。抑制齒槽轉矩除了優化電機控制算法外，還可以從電機本體結構上進行優化處理。文獻[6]從氣隙磁導的角度提出了一種新的拓撲結構，該拓撲采用不等槽寬來降低V型永磁游標電機的齒槽轉矩。也可以通過改變轉子結構來抑制齒槽轉矩。文獻[7]提出了兩種降低齒槽轉矩的方法：第一種方法是通過優化磁通屏障的形狀來最小化氣隙和轉矩脈動的波動；第二種方法是轉子開槽。文獻[8]通過對徑向磁通表面貼裝永磁無刷直流電機進行兩種不同的設計修改來降低齒槽轉矩。

文獻[9]提出了一種基于諧波轉矩抵消的動態控制來降低永磁電機中的齒槽轉矩的方法，通過研究齒槽轉矩和諧波轉矩的產生機理和周期特性，發現動態消除齒槽轉矩和諧波轉矩的可能性，并進一步研究當前諧波注入方案用于降低齒槽轉矩。

為了優化永磁同步電機伺服系統的控制性能，文獻[10]將預測函數控制(PFC)方法引入速度環的控制中。該方法將齒槽轉矩造成的擾動視為集中擾動，引入了擴展狀態觀測器(ESO)來估計集中擾動，并在PFC速度控制器中添加了基于估計擾動的前饋補償項。文獻[11]介紹了一種新的魯棒二自由度的控制技術，該技術將比例積分微分控制的概念擴展到新的方向。抑制齒槽轉矩時，常用的方法為先通過有限元分析模擬出齒槽轉矩的大小，再通過結構優化或控制抑制轉矩脈動。文獻[12]分析了磁通切換型永磁電機齒槽轉矩的產生原因，并且介紹了相應的齒槽轉矩抑制方法，主要有解析法和有限元法，同時還從本體角度分析各種抑制齒槽轉矩的方法并進行了總結概述。文獻[13]系統介紹了齒槽轉矩的產生機理。文獻[14]提出了一種基于模型預測的電機控制方法，通過引入觀測器來平衡系統的擾動，具有一定的先進性。

通過結構設計來抑制齒槽轉矩，會破壞電機的本體結構，進而降低電機的工作性能；一些特殊工況要求電機有較大的瞬時功率密度，通常電機的瞬時功率密度較大，齒槽轉矩也會隨之增加，因此通過改變電機結構來抑制齒槽轉矩的方法不適用于特殊工況。本文提出一種抑制齒槽轉矩的高精度定位伺服控制方法，在速度環中加入擴展狀態觀測器，抑制齒槽轉矩的同時，不改變電機原本的結構參數。

1 齒槽轉矩的原理

齒槽轉矩是永磁同步電機(以下簡稱PMSM)特有的且在空載情況下也會產生的周期性轉矩，而齒槽轉矩的形成是由于電機內部轉子永磁體與定子槽之間的相互作用，轉子轉向磁阻力最小方向的運動趨勢而產生的。當電機處于空載狀態時，此時存在若干個可以使轉子定位的穩定位置，穩定位置的數量由電機內部結構決定；用手轉動轉子一圈，可以明顯感覺到隨著轉子的轉動存在著大小不等的力矩，因此又將齒槽轉矩稱為定位力矩。齒槽轉矩可以表示為系統斷電時，電機內存儲的磁場能量W對定子與轉子的相對位置角度α的負導數[13]，表達式如下：

(1)

式中：Tcog是電機的齒槽轉矩；W是電機的磁共能；α是定子與轉子的相對位置角度。從式(1)可以看出，齒槽轉矩的大小會隨著定子與轉子的相對位置角度變化而變化，因此齒槽轉矩為大小不等的力矩；當轉子磁極與槽口的中心線位置對齊時，兩者之間的相互作用力矩為零，此位置為齒槽轉矩的平衡點；當轉子磁極與槽口的相對位置發生變化時，將產生阻礙轉子轉動的齒槽轉矩。將電機所有槽口與轉子磁極產生的齒槽轉矩進行疊加，即為電機的齒槽轉矩。

電機的齒槽轉矩可以通過優化結構設計與優化控制算法進行抑制，在結構設計上，可以通過改變定子結構、改變轉子結構和優化繞組設計等。對于已經加工完成的電機，再使用優化結構設計的方法抑制齒槽轉矩，會使得成本大幅增加，還可能破壞電機本身的結構，降低電機的工作性能等。因此，優化電機的控制算法不僅可以抑制齒槽轉矩帶來的影響，同時還可以降低成本，保留電機的原始工作性能。

2 齒槽轉矩的抑制

2.1 運動控制策略

為方便對PMSM的數學模型進行研究，現在作出如下假設：

1) 不計渦流、磁滯和鐵心的損耗;

2) 空間磁場在空間內呈正弦分布;

3) 定子繞組呈均勻、對稱分布。

為了方便控制器的設計，選擇id,iq和ω作為狀態變量。因此，PMSM的數學模型可以表達：

(2)

PMSM的運動方程：

(3)

式中：ω是轉子速度；id和iq是d，q軸的定子電流；ud和uq為d，q軸的定子電壓；Ld和Lq為d，q軸的定子電感，且滿足Ld=Lq=L；Rs為定子電阻；ψv是轉子磁鏈；p為極對數；J為轉動慣量；TL為負載轉矩；B為粘性摩擦系數；Kt=3pψv/2。

圖1為PMSM驅動控制系統原理圖。驅動控制系統由3個控制器、空間矢量調制(SVPWM)、逆變器、磁場定向裝置與PMSM組成。3個控制器分別為1個速度回路控制器與2個電流控制器，控制器之間采用傳統級聯的控制回路結構。其中，電流環控制器中包括兩個PI控制器，分別用來穩定d-q軸的當前跟蹤誤差。

圖1 PMSM驅動控制系統原理圖

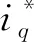
PI控制具有簡單、穩定性好、工作可靠、調整方便等優點，被廣泛應用于工業控制中。在速度環控制器中，依舊采取PI控制器，在此處不再贅述PI控制的原理。可以通過調整kp和ki提高速度環帶寬，提升增益，進而達到良好的控制效果；為了提升PI控制器的抗干擾性能，在速度環控制器中除了PI反饋部分外，還引入前饋補償部分對系統擾動進行補償。

考慮使用相應的前饋補償控制方法，擴展狀態觀測器(以下簡稱ESO)作為一種干擾估計技術被引入PMSM驅動控制系統中。

圖2為復合PI+ESO控制器的原理圖。從圖2中可以得出，復合控制器的輸出為ω，因此式(2)中的電機動力學方程可以表示：

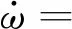
(4)

圖2 PI+ESO復合控制器原理圖

此時，定義x2=d(t)，x1=ω，式(4)可以表達為狀態方程組：

(5)

式中：c(t)為系統的不確定性以及總干擾d(t)的變化率。將式(4)表示為二階線性ESO系統：

(6)

式中：-p為ESO的極點，并且有p>0；z1為速度ω的估計值；z2為系統集總擾動d(t)的估計值；b0為Kt/J的估計值。根據文獻[11]，z1(t)→ω(t) ，z2(t)→d(t)。基于此信息，可以實現干擾補償。

2.2 仿真研究

為了驗證本文的齒槽轉矩抑制策略的有效性與準確性，下面利用仿真工具搭建PMSM驅動控制系統。PMSM負載端輸入模擬量大小為1 N·m、以正弦分布的模擬齒槽轉矩；不額外增加負載，即模擬PMSM在空載情況下，通過仿真比較PI與PI+ESO的控制效果。PMSM的參數：電機的額定電壓為48 V(DC)，額定電流為23 A，額定功率為1.2 kW，額定轉矩為23 N·m，額定轉速為500 r/min，峰值轉矩為88 N·m，瞬時最大電流為92 A，極對數為4，電機磁鏈為0.11 Wb，線電阻0.1 Ω，線電感0.6 mH，轉子轉動慣量為0.005 25 kg·m2。

仿真主要分為兩個部分：第一部分為速度波動的抑制，通過指定轉速對比PI與PI+ESO 2種控制方法，驗證PI+ESO的控制方法對低速狀態下電機的速度波動有更好的抑制效果；第二部分為到位精度的測試，由于齒槽轉矩的存在，轉子在到達某一指定位置時的精度與時間都會受到影響，通過給定位置指令對比PI與PI+ESO 2種控制方法的到位精度與到位時間，驗證PI+ESO的控制方法在同一位置指令下到位精度更高。

圖3為指定轉速為10 r/min時，基于速度環PI控制方法的速度曲線。此時，運動全程由速度環和電流環控制，電機速度環參數Kp=1.2，Ki=3.2。從圖3中可以看出，實際轉速的波動較大，且實際轉速與指令轉速的誤差約在±11 r/min，誤差較大。

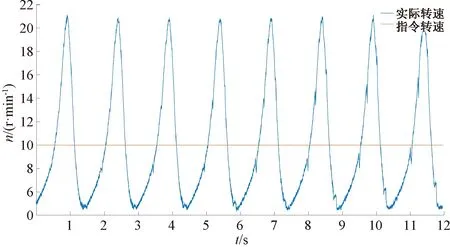
圖3 指令轉速為10 r/min采用PI控制的實際轉速

圖4為指定轉速為10 r/min時，基于速度環PI+ESO配合協調控制的速度曲線。此時引入了ESO，在速度環PI參數不變的情況下可以清晰地看到，實際轉速的波動明顯減小，實際轉速與指令轉速的誤差約在±0.5 r/min，誤差明顯減小。

圖4 指令轉速為10 r/min采用PI+ESO控制的實際轉速

圖5為指令位置為180°時，基于速度環PI控制的位置曲線。此時電機位置環的Kp為10.5，Ki為0，電機速度環參數Kp=1.2，Ki=3.2。從圖5中可以看出，轉子位置收斂于指令位置時，存在0.4°左右的超調，且收斂過程中有振蕩。

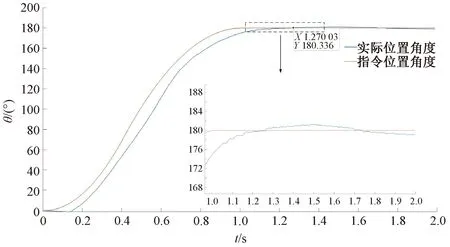
圖5 指令位置為180°采用PI控制的轉子實際位置

圖6為指令位置為180°時，基于速度環PI+ESO配合協調控制時的電機轉子位置曲線 。在保證電機位置環、速度環PI參數不變的條件下，從圖6中可以看出，轉子實際位置的位置曲線較PI控制時得到明顯提高，最大超調量為0.025°，最終轉子位置收斂于指令位置。

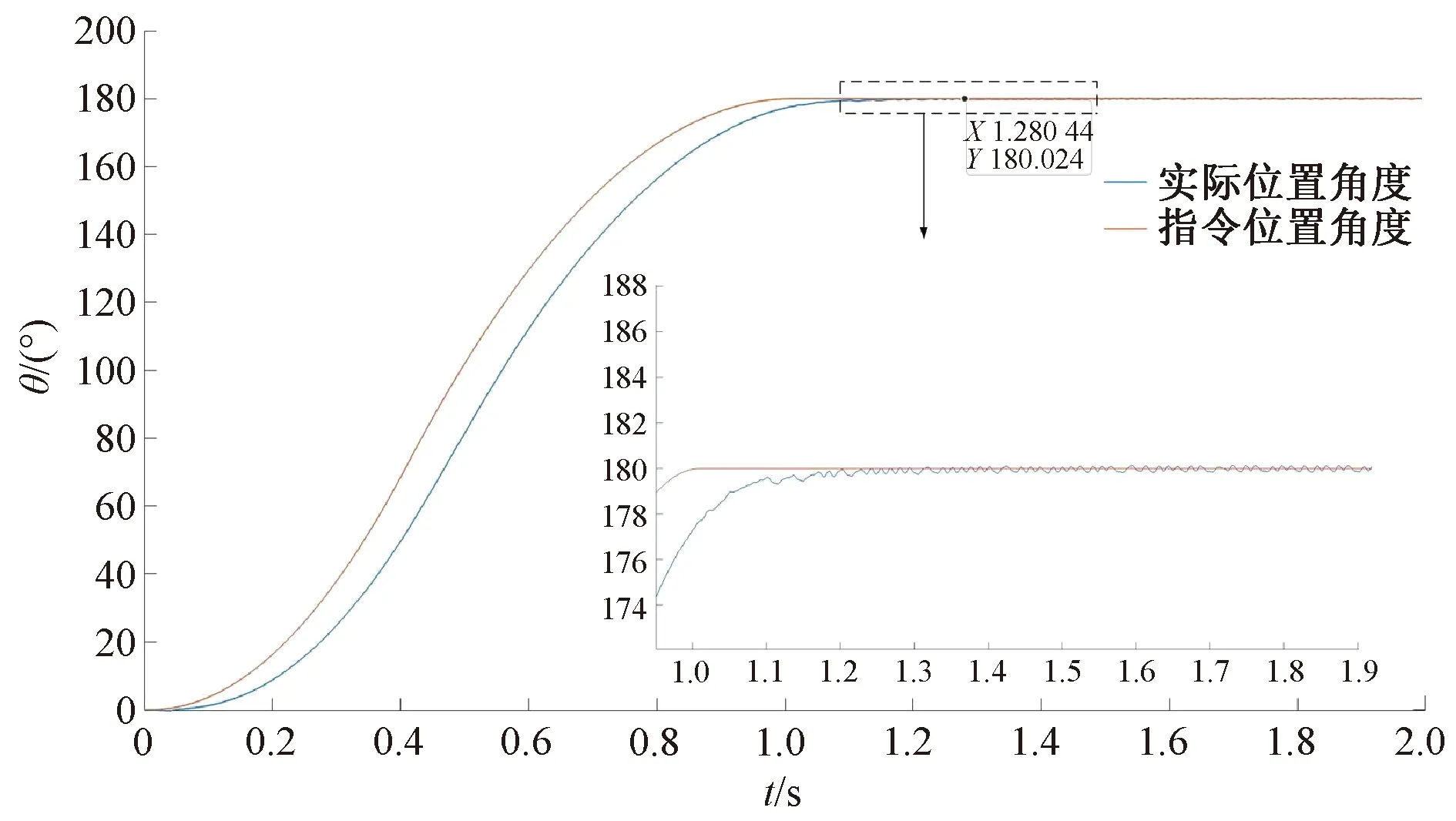
圖6 指令位置為180°采用PI+ESO控制的轉子實際位置

3 實驗驗證

3.1 齒槽轉矩的測量

通過手動測量的方法將電機的齒槽轉矩平衡點與齒槽轉矩最大點找出，方便在后續到位精度實驗時進行到位誤差的對比。

在測量電機的齒槽轉矩數值時，系統處于失電狀態，控制器通電，使用力矩扳手將轉子轉動到某個位置，通過觀測轉子位置角度，記錄當前時刻轉子的位置與力矩扳手上顯示的數值。為方便測量，只記錄齒槽轉矩為零的位置與齒槽轉矩最大的位置，經過測量可以發現，電機的齒槽轉矩約為1 N·m。表1為轉子位置角度與齒槽轉矩大小的對應關系表。

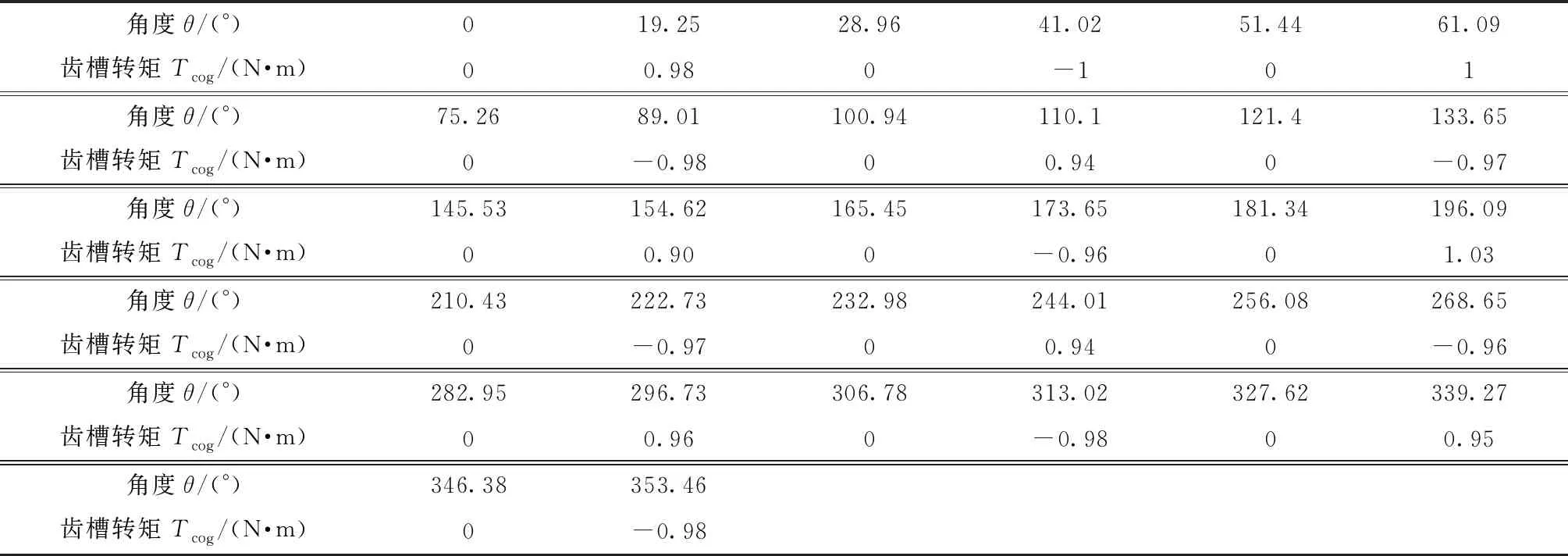
表1 轉子位置與齒槽轉矩的關系

圖7為根據表1得出的齒槽轉矩分布位置圖。經測量，當轉子位置位于196.09°附近時，此時的齒槽轉矩最大約為1.03 N·m。圖8為測量齒槽轉矩的過程圖,當前位置時，齒槽轉矩約為0.98 N·m。

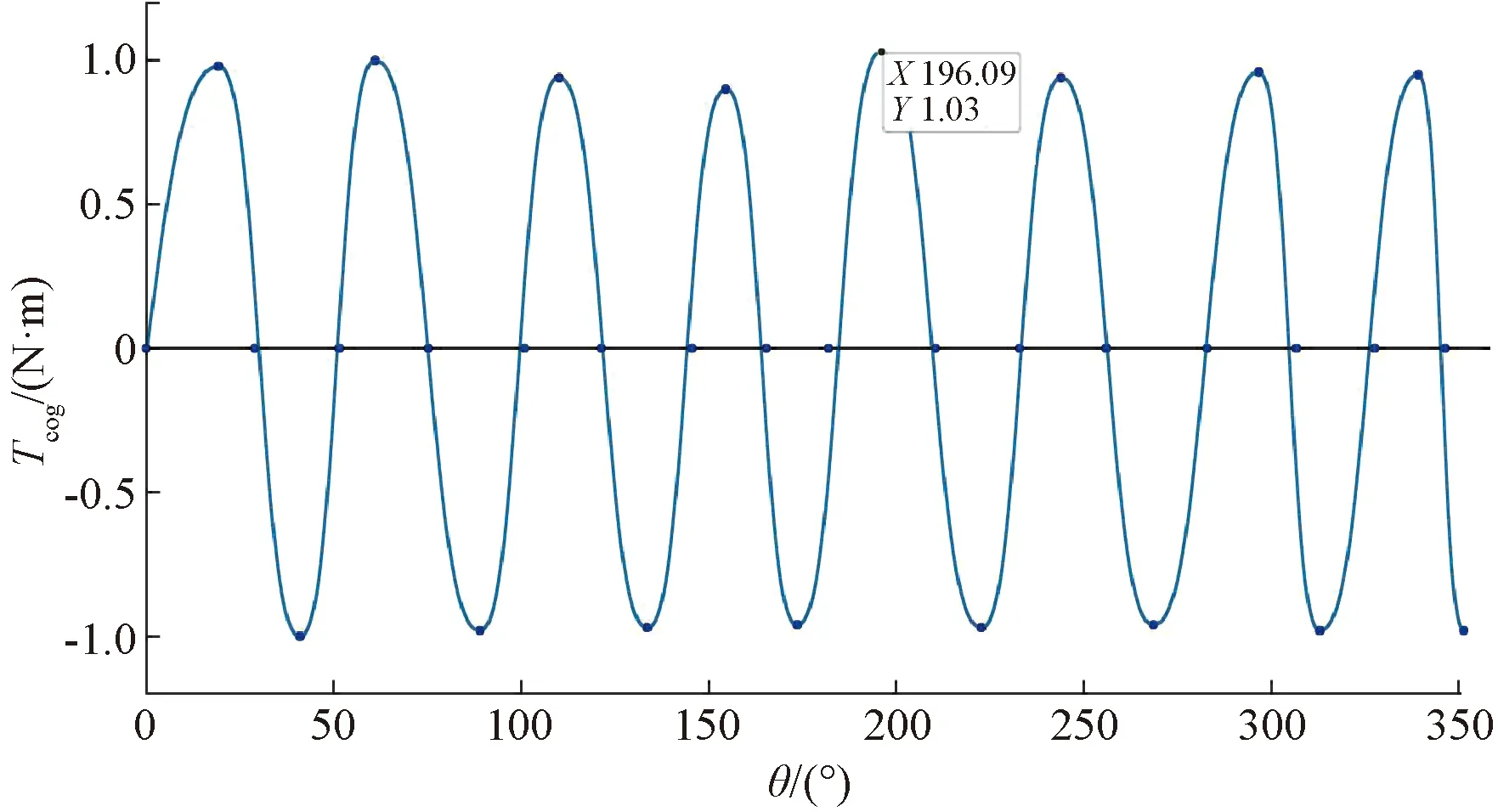
圖7 齒槽轉矩分布位置圖

圖8 齒槽轉矩測量原理圖

3.2 到位精度實驗

為了驗證本文齒槽轉矩抑制策略的有效性，搭建電機控制系統的實驗平臺，實驗平臺如圖9所示。

圖9 電機控制系統實驗平臺

實驗使用的電機控制系統實驗平臺主要由實驗電機、電源、CCS監控軟件、驅動器、數據采集計算機以及CAN分析儀組成。為更清晰地模擬齒槽轉矩抑制的效果，經過設計特定齒槽轉矩的PMSM在空載低速狀態下運行。電機驅動控制器為基于數字信號處理器(DSP)設計的硬件平臺，DSP芯片為TMS320F28379，其中轉子位置通過16位旋變解碼芯片反饋給控制器。實驗中使用CAN分析儀采集數據，并在仿真平臺中使用虛擬示波器進行顯示與保存數據。

實驗中所用的PMSM的各項參數與仿真一致。轉子運動到指定位置時，到位誤差要求在0.1°。通過上一節對于齒槽轉矩的測試可以得出齒槽轉矩的平衡點與齒槽轉矩最大的點：轉子位置60°左右時，齒槽轉矩的值約為1 N·m；轉子位置180°左右時，齒槽轉矩的值約為0。因此選取指定位置為60°與180°的到位精度測試，便于驗證本文控制方法的有效性。

當指令位置為60°，位置環Kp=10.5，Ki=0，速度環Kp=1.2，Ki=3.2時，采用PI與PI+ESO控制方法的到位精度測試結果如圖10所示。從圖10(a)可以看出，此時電流波動較小，實際轉速與指令轉速誤差較大，實際轉速波動較大；從圖10(b)可以看出，當增加ESO后，實際轉速的波動明顯減小，實際位置曲線也有明顯改善，為了抑制齒槽轉矩帶來的影響，電流波動明顯增加。

圖10 指令位置為60°采用PI與PI+ESO控制的到位精度測試

圖11為指令位置為60°，采用PI與PI+ESO控制方法的速度誤差與位置誤差圖。從圖11(a)可以看出，最終實際位置與指令位置的誤差約為0.6°，并未達到要求精度誤差，而實際轉速與指令轉速的誤差較大；從圖11(b)可以看出，增加了ESO以后，實際轉速與指令轉速的誤差明顯減小，轉子到達指令位置后，位置誤差約為0.05°，通過ESO消除了最終的到位誤差，提升了到位精度。

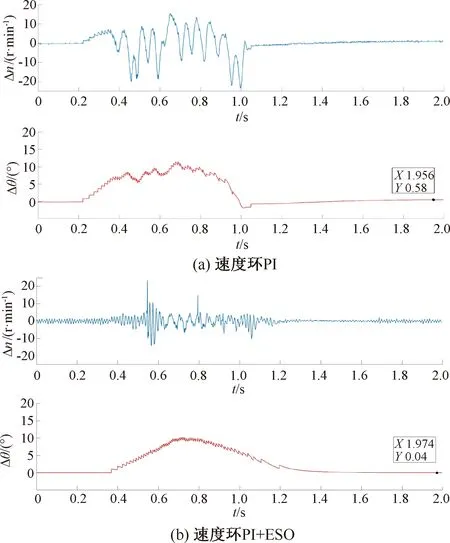
圖11 指令位置為60°采用PI與PI+ESO控制的速度誤差與位置誤差

當指令位置為180°，位置環Kp=10.5，Ki=0，速度環Kp=1.2，Ki=3.2時，采用PI與PI+ESO控制方法的到位精度測試結果如圖12所示。從圖12(a)可以看出，電流波動較小，實際轉速與指令轉速的誤差較大，在轉子到達指定位置的過程中也有波動；從圖12(b)可以看出，當增加ESO后，轉速波動減小，與指令轉速擬合程度增大，轉子到位過程中波動減小，為抑制齒槽轉矩帶來的影響，電流波動明顯增加。

圖12 指令位置為180°采用PI與PI+ESO控制的到位精度測試

圖13為指令位置為180°，采用PI與PI+ESO控制方法的速度誤差與位置誤差圖。從圖13(a)可以看出，轉子到達指定位置的到位精度誤差約為0.1°，相較于60°到位實驗同樣采取PI控制時，到位精度誤差明顯減小；從圖13(b)可以看出，增加了ESO以后，實際轉速與指令轉速的誤差減小，轉子到達指令位置后，到位誤差被縮小至0.05°，通過增加ESO提升了到位精度，驗證了本控制方法的有效性。

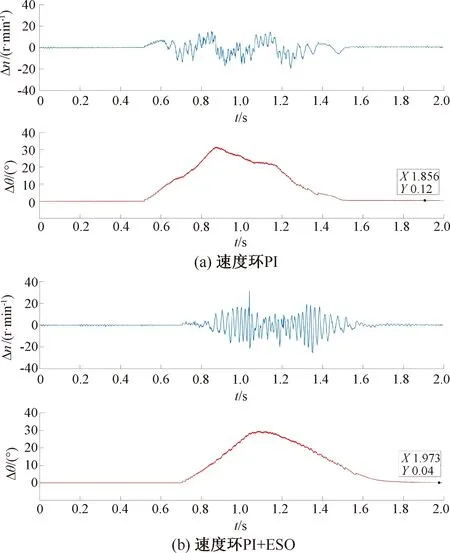
圖13 指令位置為180°采用PI與PI+ESO控制的速度誤差與位置誤差

3.3 速度波動抑制實驗

設置指定轉速3 r/min和10 r/min，進行速度波動抑制實驗。由于齒槽轉矩的存在，當采取傳統控制方法時，實際轉速會受齒槽轉矩的影響而產生較大的波動；而當采取本控制方法后，實際轉速的波動得到明顯的抑制，實際轉速與指令轉速的誤差也明顯縮小。

當指令轉速為3 r/min，速度環Kp=1.2，Ki=3.2時，采用PI與PI+ESO控制方法的轉速測試結果如圖14所示。從圖14(a)可以看出，轉子3 r/min的轉速低速旋轉時，實際轉速與指令轉速的誤差較大(約為20 r/min)，齒槽轉矩的存在使實際轉速極不穩定，轉速誤差也很大；從圖14(b)可以看出，增加了ESO以后，速度波動抑制得到明顯改善，實際轉速與指令轉速擬合程度增加，轉速誤差明顯縮小。

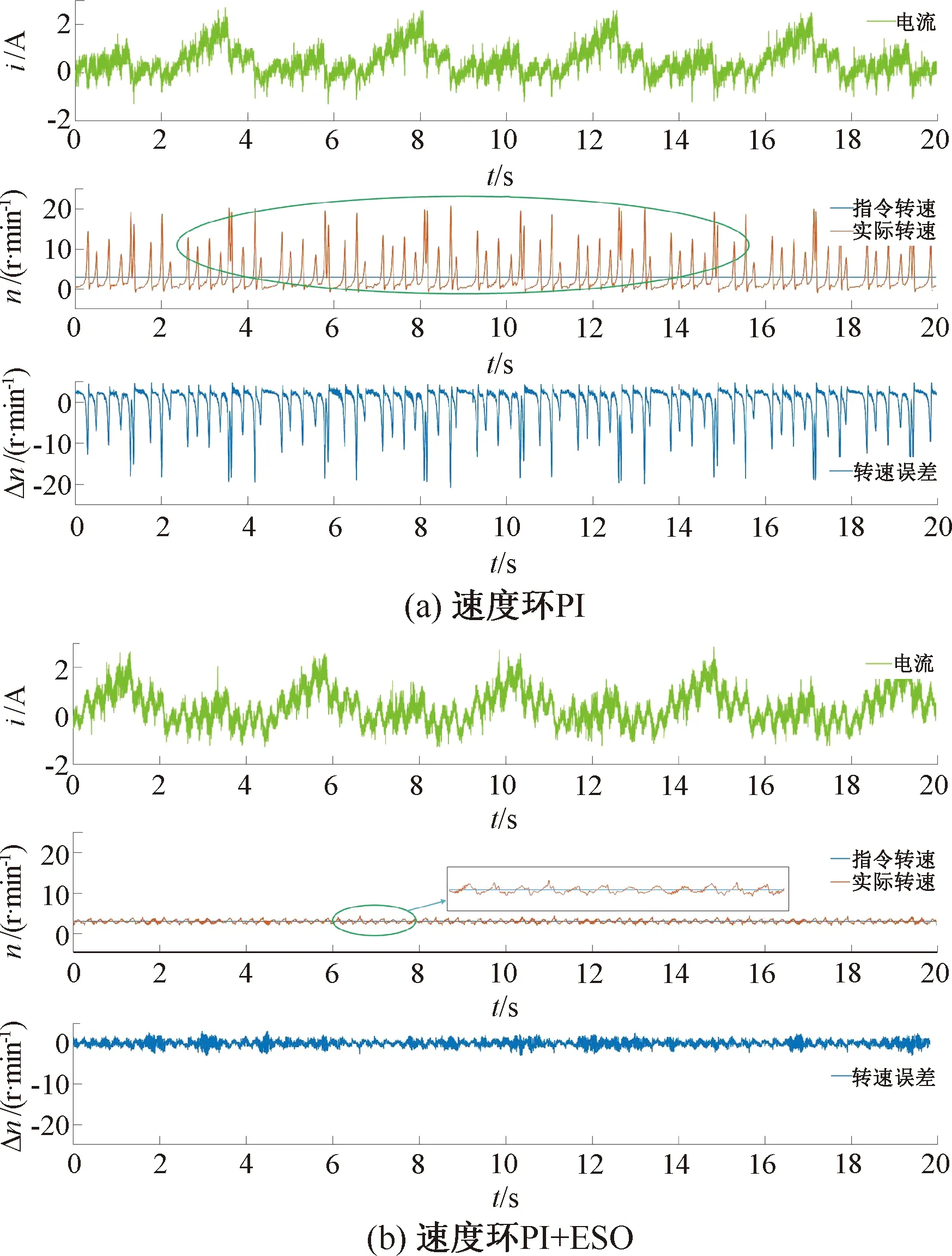
圖14 指令轉速為3 r/min 采用PI與PI+ESO控制的速度波動抑制測試

指令轉速為10 r/min，速度環Kp=1.2，Ki=3.2時，采用PI與PI+ESO控制方法的轉速測試結果如圖15所示。從圖15(a)可以看出，實際轉速波動較大，實際轉速與指令轉速的誤差約為±12 r/min；從圖15(b)可以看出，增加了ESO以后，實際轉速的波動得到了抑制，實際轉速與指令轉速的誤差也縮小到了約±3 r/min。

通過兩組指定轉速實驗驗證了本控制算法對于速度波動抑制的有效性。

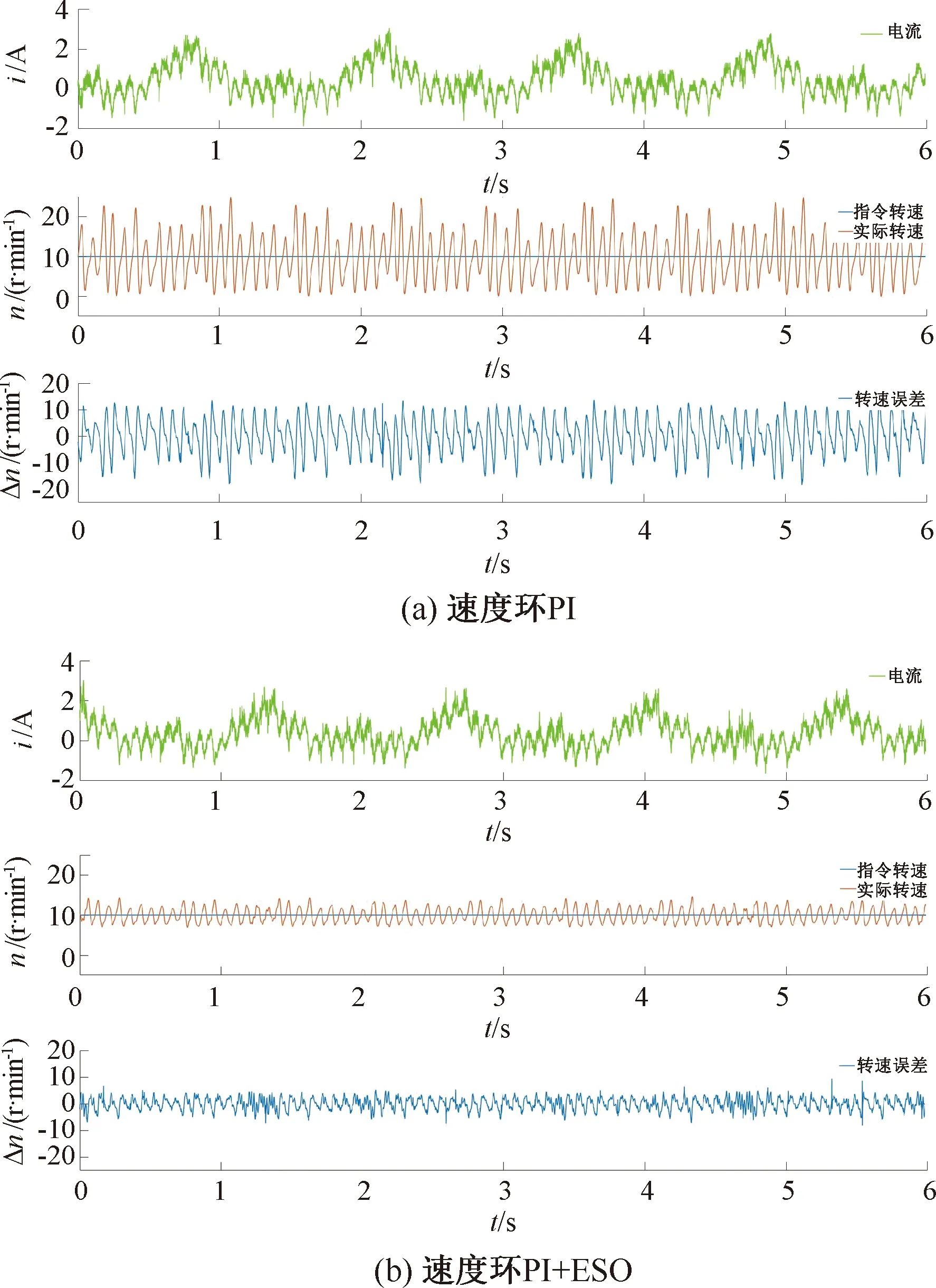
圖15 指令轉速為10 r/min 采用PI與PI+ESO控制的速度波動抑制測試

4 結 語

針對PMSM在低速狀態運行下由齒槽轉矩帶來的速度波動問題與輸入指令位置時電機的到位精度問題，本文提出了應用速度環PI+ESO的控制方法對齒槽轉矩帶來的影響進行抑制，通過到位精度實驗與速度波動抑制實驗，驗證了本文控制算法對于齒槽轉矩抑制的有效性。