一種可穩定計算負躍層淺海環境下聲場的波數積分方法

于曉林，許偉杰，楊春梅，駱文于

(1.中國科學院聲學研究所東海研究站，上海 201800；2.自然資源部第一海洋研究所，山東青島 266100；3.中國科學院聲學研究所聲場聲信息國家重點實驗室，北京 100190)

0 引言

在夏、秋季節，淺海中常存在較強的負躍層。在負躍層海域，海水可以分成三層，最上層以及最下層的聲速隨深度變化緩慢，兩層之間的中間層的聲速變化劇烈。淺海負躍層對水下聲監測、漁業生產、艦艇航行等有極大的影響[1]，因此對淺海負躍層聲傳播規律的研究極為重要[2]。

波數積分方法首先是由Pekeris引入到水聲學中的[3]，簡正波[4-5]方法是通過復圍線積分法計算該積分，得到的是不同階簡正波對應的留數之和，而波數積分方法是通過直接對波數進行數值積分求解的，國內外許多學者對波數積分方法進行了相應的研究[6-8]。在某些低頻淺海環境下，波數積分算法的計算結果比簡正波方法更準確[9]。

文獻[10]提出了一個負躍層淺海環境中的波數積分解法，該解法在理論上是正確的，但是在實際的仿真中發現，當水平波數的取值過大時，會造成艾里(Airy)函數的數值溢出，系數矩陣存在數值不穩定的現象。為了解決文獻[10]中給出的解法中存在的數值不穩定的問題，本文通過合理地歸一化，提出了一種負躍層淺海環境下無條件穩定的波數積分方法。

1 理論推導

1.1 波數積分理論

1.2 負躍層淺海環境下不穩定的波數積分算法

文獻[10]給出了計算負躍層淺海環境下的深度格林函數的線性方程組，該線性方程組在理論推導上是沒問題的，但是由于未對Airy函數做任何的變換，因此在實際的仿真中，系數矩陣存在數值不穩定現象。下面簡單介紹下文獻[10]中給出的線性方程組并分析其不穩定的原因，然后通過對Airy函數合理的變換，從而求得穩定的深度格林函數。

負躍層淺海環境中的聲速如式(5)所示。

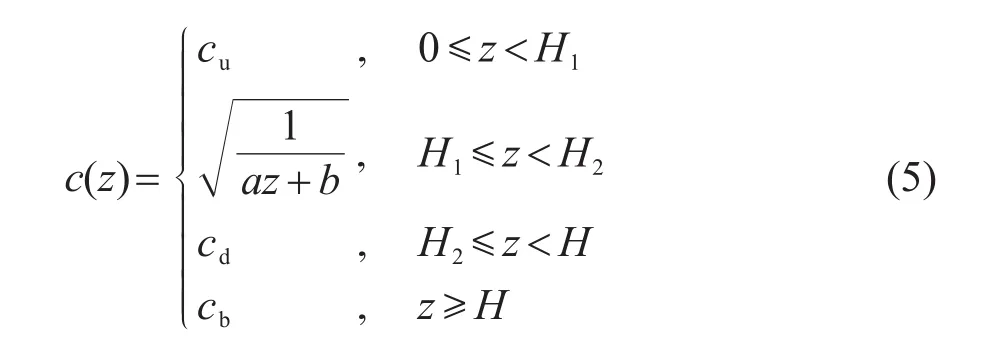
其中：cu為第一層中的聲速，cd為第三層中的聲速，cb為海底聲速，ρw為海水密度，ρb為海底密度，H為海水深度，H1、H2分別為負躍層的起、止深度。

以聲源位于第一層為例，各層中的線性方程可以表示如下[11]：

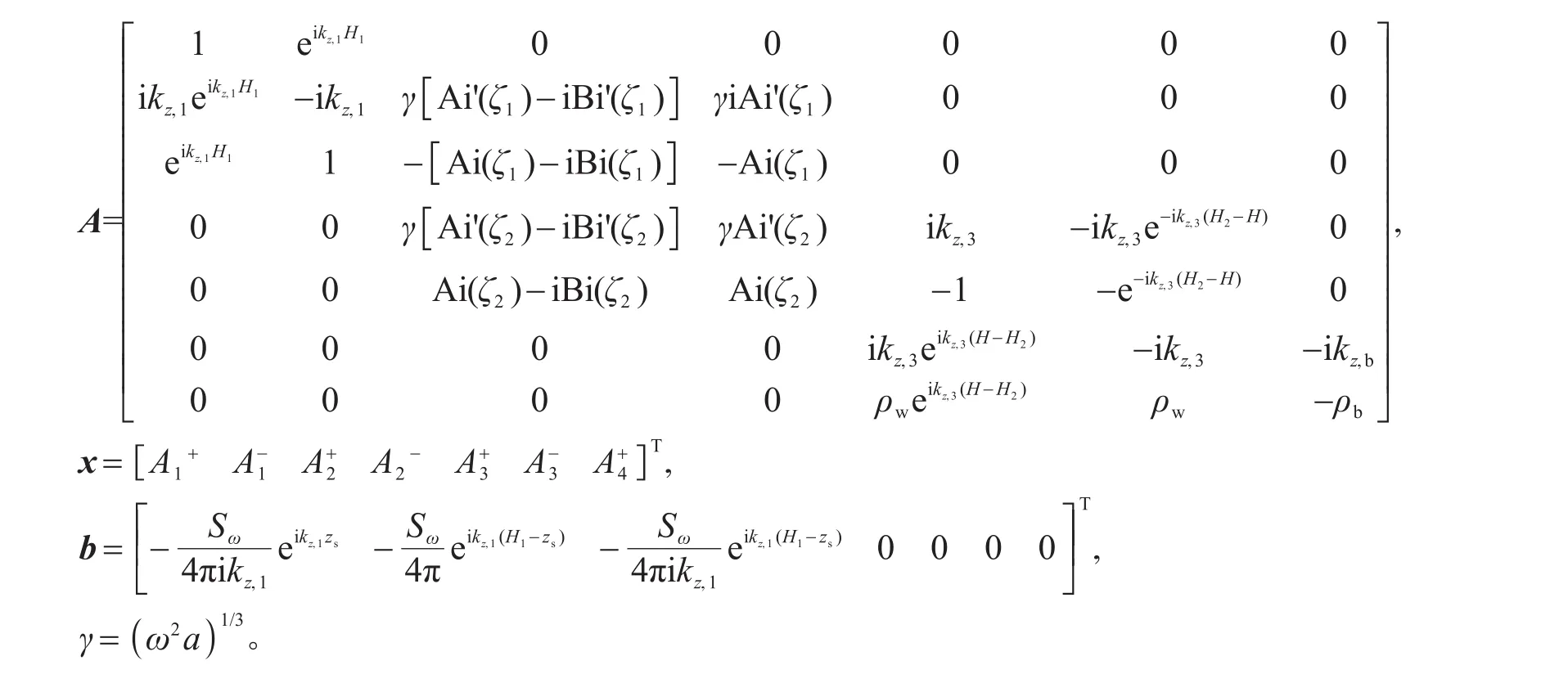
該矩陣方程的系數矩陣里存在趨于無窮大的項Bi(ζ)以及Bi'(ζ)，因此可能存在數值溢出的現象。在仿真中發現，當水平波數取值大于第三層海水波數k3時，仿真計算會提示矩陣接近奇異值、結果可能不準確的警告。可見，由于Airy函數的漸近特性，該深度格林函數的解在數值上是不穩定的，為了解決該問題，需要在系數項里避免趨于無窮大的項Bi(ζ)以及Bi'(ζ)，因此本文提出了一種無條件穩定的波數積分算法。

1.3 負躍層淺海環境下穩定的波數積分算法

由于Airy函數的漸近特性，上述得到的矩陣方程存在數值不穩定的問題，下面給出一種數值穩定的計算方法。負躍層淺海環境中，聲源位于第一層、第三層、第二層時的示意圖如圖1～3所示。

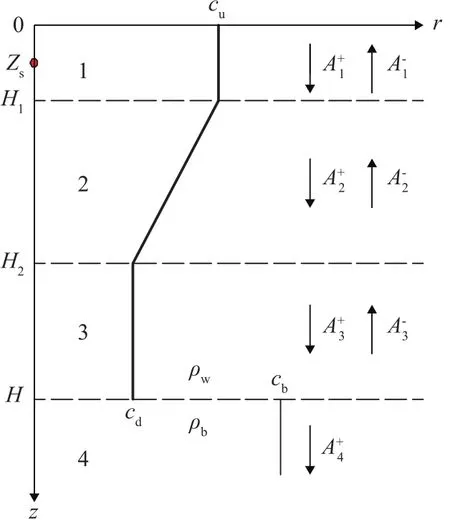
圖1 聲源處于第一層Fig.1 The sound source in the first layer

1.3.1 聲源處于第一層時的矩陣方程

為了避免系數矩陣的系數項是奇異矩陣，需要對Airy函數進行變換，將Airy函數表示成式(22)中的形式[12]：

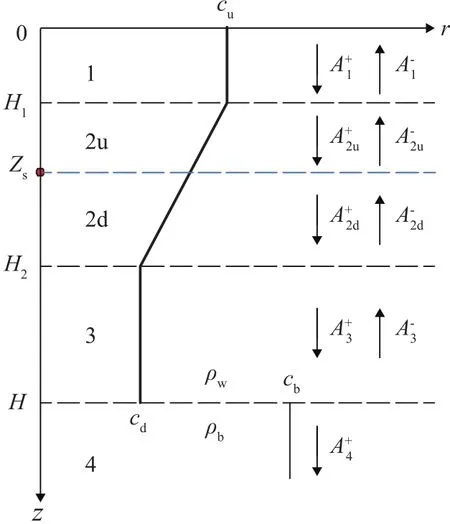
圖2 聲源處于第三層Fig.2 The sound source in the third layer

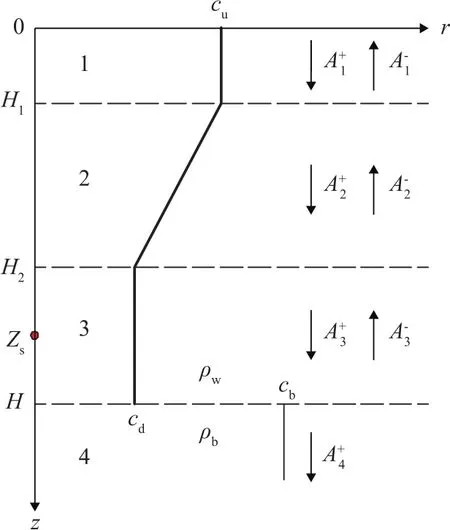
圖3 聲源處于第二層Fig.3 The sound source in the second layer

該矩陣方程的系數項不存在趨于無窮大的項Bi(ζ)以及Bi'(ζ)，是無條件穩定的，可以求得未知變量，然后通過式(6)～(9)求得聲源在第一層時，各個層的深度格林函數，最后利用式(3)可以求得聲場的位移勢能，從而求得各個層的聲場。

1.3.2 聲源處于第三層時的矩陣方程

當聲源處于第三層時，同樣可以得到聲源位于第三層時的無條件穩定的矩陣方程：

此時：A、x與式(30)中取值相同，b的取值如下：

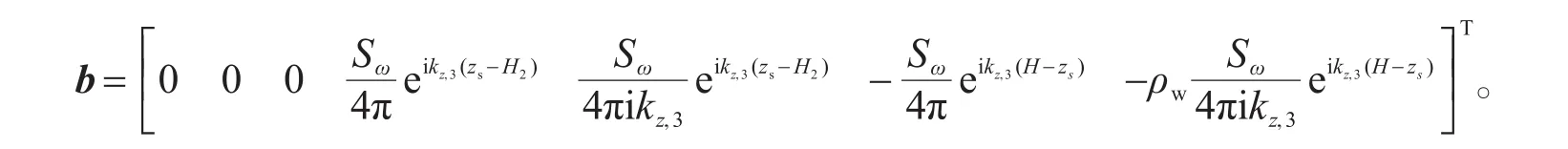
通過該矩陣方程，可以求得7個未知變量，進而求得總聲場。

1.3.3 聲源處于第二層時的矩陣方程

當聲源處于第二層時，需要在聲源深度處構建一個虛擬界面，同時在該虛擬邊界z=zs處添加兩個邊界條件：

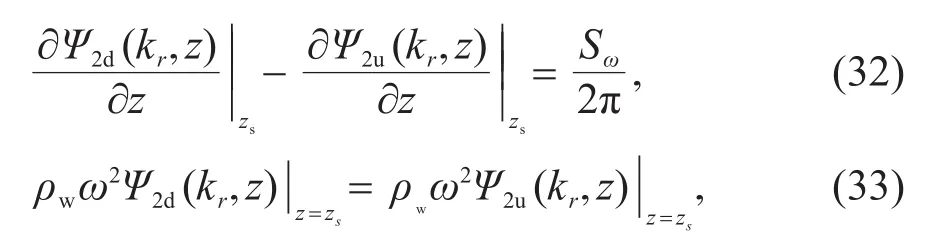
從而得到聲源位于第二層的矩陣方程：

此時：

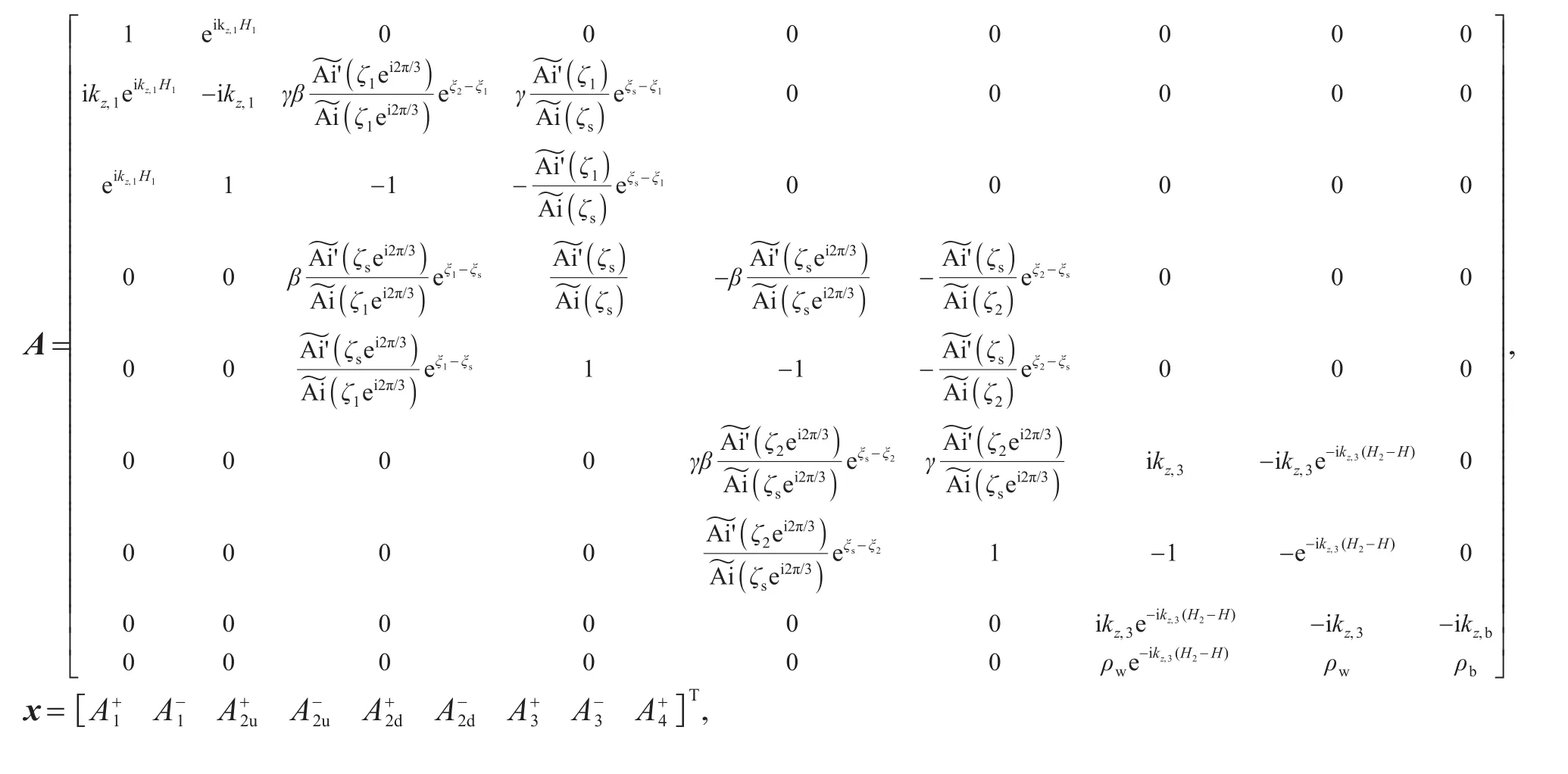
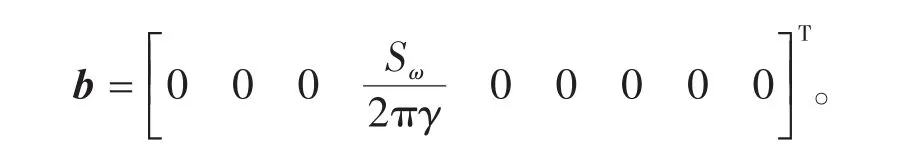
利用該矩陣方程，可以求出9個未知變量，進而求得總聲場。

1.4 聲場計算

通過前面的推導，可以得到聲源位于三個層中的無條件穩定的深度格林函數，再利用式(3)可以得到聲場的位移勢。在實際的仿真中，對格林函數尖峰的欠采樣，容易引入較大的誤差。為了解決這一問題，采用復圍線積分的方法[11]：

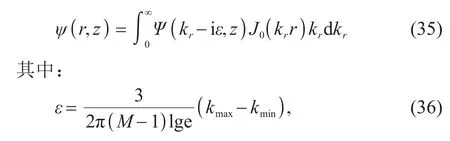
式中：M是采樣點數，kmax為數值積分的上限，kmin為數值積分的下限。

2 數值算例

考慮圖4的海洋環境，海洋環境為負躍層淺海環境，海水深度為100 m，海水密度為1.0 g·cm-3，0～25 m的聲速為1 500 m·s-1，25～45 m的聲速由1 500 m·s-1變為1 460 m·s-1，45～100 m的聲速為1 460 m·s-1，海底聲速為1 800 m·s-1，海底密度為1.8 g·cm-3，海底吸收系數為0.15 dB·λ-1。

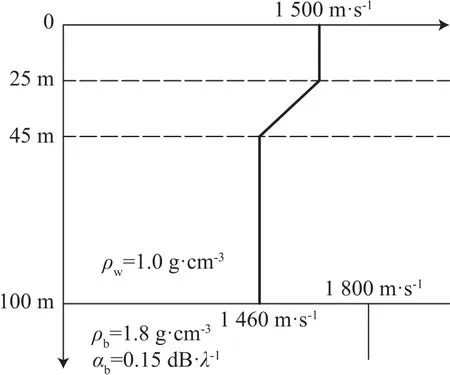
圖4 負躍層淺海聲場計算實例的海洋聲速剖面示意圖Fig.4 A typical sound speed profile for sound field calculation in the shallow-water with a negative thermoclines

分別將聲源置于第一層等聲速層以及第二層負躍層中，比較數值不穩定的算法與本文所提出的數值穩定的解法的結果差異：對于數值不穩定算法來說，水平波數最大取值只能取到第三層海水中波數k3附近，其中k3=ω/cd，當水平波數的取值超過k3值時，系數矩陣存在數值不穩定的現象，線性方程求解器在求解時會發生預警；而對于優化后的算法來說，水平波數可以取到一個極大值。在實際的仿真計算中，水平波數的取值應該根據算例的具體情況來確定：理論上，為保證格林函數的收斂性，水平波數的取值應該越大越好，但是為保證計算效率，水平波數取值又應該越小越好。對于本算例來說，1.2k3是一個可以保證格林函數收斂到0值附近的極小取值，因此本文中優化后算法的水平波數一律取到1.2k3。圖5是聲源位于20 m(聲源在第一層)時，各層的深度格林函數。在本算例中，數值不穩定算法的深度格林函數的水平波數最大值只能取到k3(即0.215)，優化后的算法的水平波數最大取值為1.2k3(即0.258)時，就可以保證該算例下深度格林函數的收斂性。圖6給出相應的傳播損失結果。

圖6 聲源深度為20 m，不同接收深度處的傳播損失計算結果（穩定與不穩定波數積分算法對比）Fig.6 The transmission losses at different depths for the sound source at the depth of 20 m(comparison between stable and unstable wave-number integral algorithms)

圖7是聲源位于40 m(聲源在第二層)時，不同深度的深度格林函數，可以看到，當接收深度為40 m時，數值不穩定算法的深度格林函數不能收斂到0附近，而優化后的算法可以保證深度格林函數的足夠收斂性。圖8給出了相應的傳播損失結果。

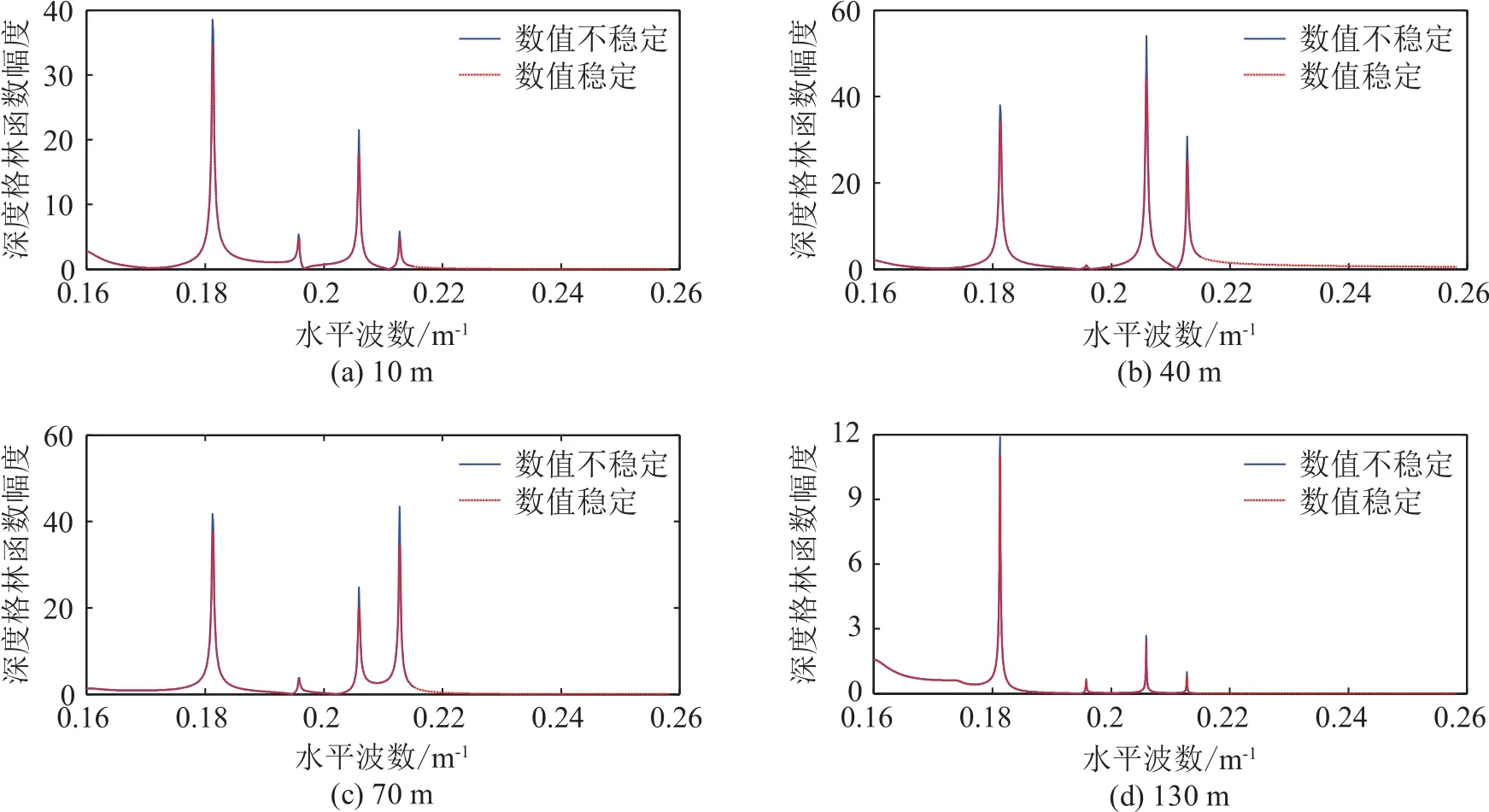
圖7 聲源深度為40 m，不同接收深度處的深度格林函數計算結果（穩定與不穩定波數積分算法對比）Fig.7 The magnitudes of the Green’s function at different depths for the sound source at the depth of 40 m(comparison between stable and unstable wave-number integral algorithms)

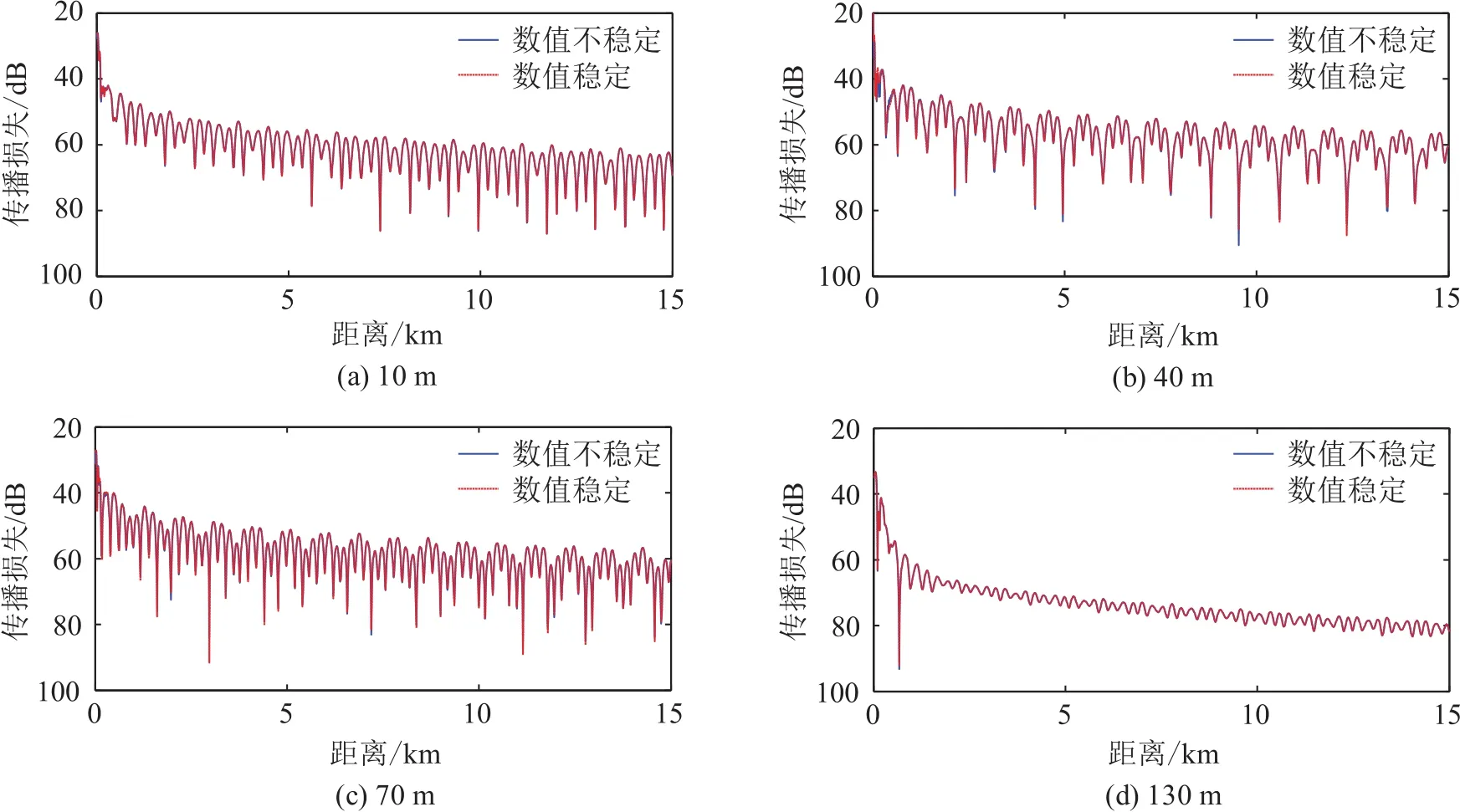
圖8 聲源深度為40 m，不同接收深度處的傳播損失的計算結果(穩定與不穩定波數積分算法對比)Fig.8 The transmission losses at different depths for the sound source at the depth of 40 m(comparison between stable and unstable wave-number integral algorithms)

為了進一步驗證本文所提方法的準確性，比較本文所提方法的計算結果與簡正波模型KRAKENC的計算結果[14]，圖9給出聲源深度在20 m(聲源位于第一層)時各個接收深度的傳播損失結果，圖10給出聲源深度在40 m(聲源位于第二層)時的各個接收深度的傳播損失結果。結果顯示，兩種方法的計算結果吻合得較好。由于簡正波方法在某些低頻淺海環境中的近場計算上存在誤差[9]，因此本文所提方法可以作為負躍層淺海環境中聲場計算的有效補充。

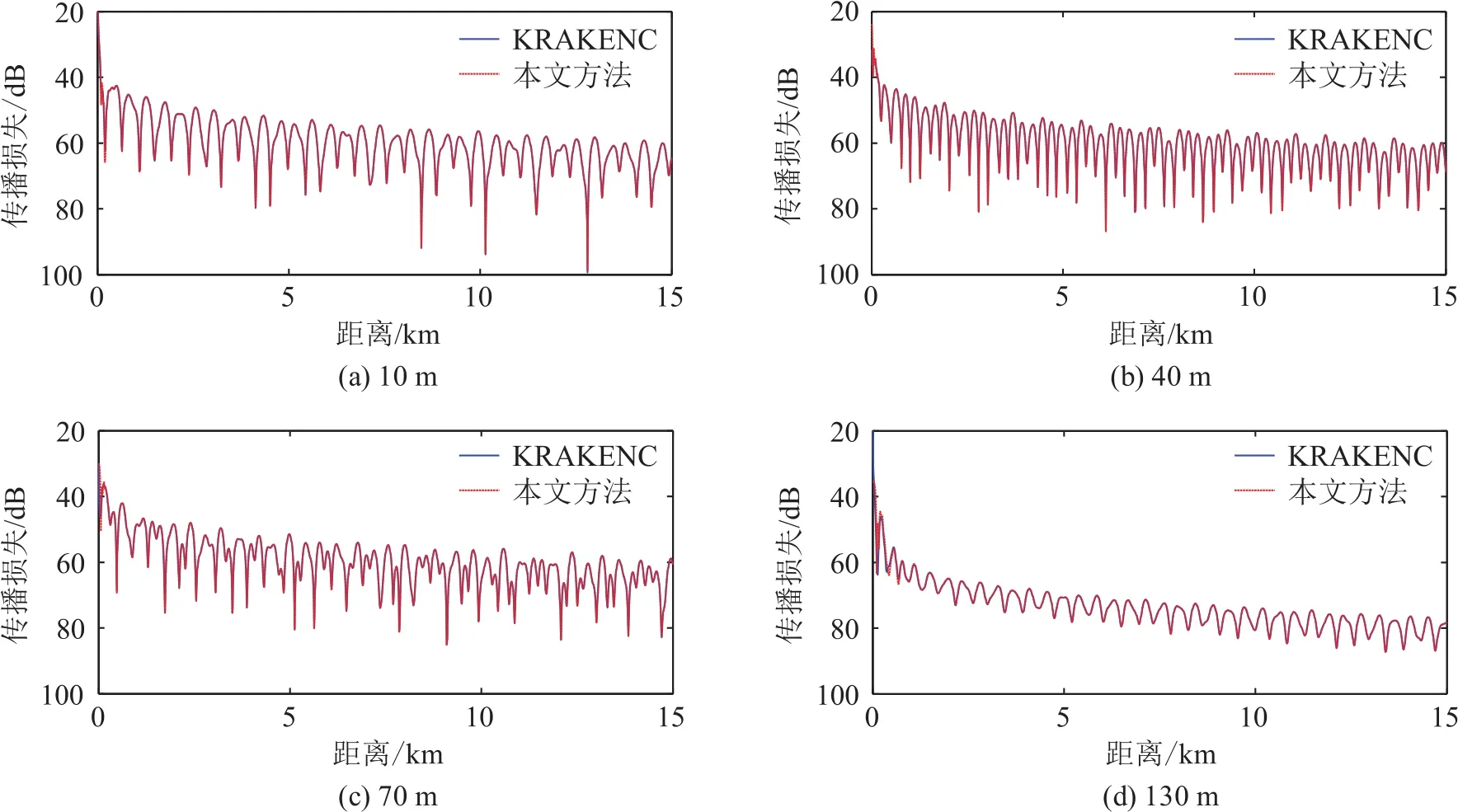
圖9 聲源深度為20 m，不同接收深度處的傳播損失的計算結果(本文算法與KRAKENC算法對比)Fig.9 The transmission losses at different depths for the sound source at the depth of 20 m(comparison between the proposed algorithm and KRAKENC algorithm)

圖10 聲源深度為40 m，不同接收深度處的傳播損失的計算結果(本文算法與KRAKENC算法對比)Fig.10 The transmission losses at different depths for the sound source at the depth of 40 m(comparison between the proposed algorithm and KRAKENC algorithm)

3 結論

本文通過對Airy函數的處理，得到了負躍層淺海環境下無條件穩定的波數積分方法。該方法保持了系數矩陣方程中的數值穩定性，避免了由于數值不穩定造成的深度格林函數的收斂性不足的問題，能夠提高負躍層淺海環境下聲場計算的穩定性。

將本文所提方法與簡正波模型KRAKENC的計算結果進行比較，結果顯示，兩種方法有很好的一致性。本文所提的方法在數值上是穩定的，并且可以直接通過穩定的系數矩陣方程求得相應的解析解。因此，本文所提的方法可以作為負躍層淺海環境中聲場計算的有效補充。