氣囊式可調頻動力吸振器性能研究

李 創，徐 偉，胡澤超，邱元燃

(1. 海軍工程大學 振動與噪聲研究所，湖北 武漢 430033；2. 船舶振動噪聲重點實驗室，湖北 武漢 430033)

0 引 言

被動式動力吸振器的有效吸振帶寬較窄，無法滿足激勵頻率變化較大情況下的減振需求，因此需要對吸振器施加主動控制來實現寬頻帶內的吸振。主動式動力吸振器分為全主動式和半主動式。由于半主動式動力吸振器具有耗能少、控制簡單、穩定性好等優點，近年來得到了廣泛研究。目前研究的成果有機械式、電磁式、新材料式和變質量-負剛度式半主動動力吸振器等。

以上結構設計主要適用于解決小型設備的振動問題，對于大型或超大型機械設備，需要獲得較大質量比，上述吸振器存在作動力不足等問題。基于氣囊大載荷特性，以氣囊為剛度元件的半主動動力吸振器設計引起了廣泛關注。Brennan利用氣囊設計了一種半主動動力吸振器，通過改變氣囊壓力大小來調節吸振器剛度，拓寬了吸振器的工作頻帶，該設計可以提供較大的作動力，但其并未建立系統的動力學模型。靳曉雄設計一種應用于汽車發動機上的基于氣囊的半主動動力吸振器，進一步建立系統的動力學模型，并對吸振效果進行仿真，但未分析阻尼因素對吸振效果的影響。為了拓寬氣囊式動力吸振器的工作帶寬，提高吸振器吸振效果和適用性，亟需建立完善的系統動力學模型。

本文提出一種氣囊式可調頻動力吸振器，以氣囊作為剛度元件，通過調節氣壓來改變吸振器剛度，達到調節其吸振頻率的目的。通過節流孔連接上、下2個氣囊，調節節流孔大小改善該吸振器的阻尼特性，因此吸振器具有較寬的吸振頻帶和較好的吸振效果。同時由于氣囊具備大承載特性，該吸振器的質量可以設計的足夠大，能夠提供較大的作動力，滿足對大型設備的吸振需求。

1 結構原理

該吸振器由螺桿、氣囊、質量塊、節流孔、上頂板、下底板組成，如圖1所示。中間質量塊與上、下氣囊固接，上、下氣囊分別與上頂板和下底板固接。通過調節氣囊壓力，使吸振器固有頻率與激勵頻率一致，從而抑制設備振動。阻尼是吸振器的重要參數，存在一個最優阻尼值使吸振器的吸振效果最優。該吸振器采用節流孔連接2個氣囊，氣囊振動過程中會在節流孔兩側形成壓力差，氣體在壓力差的作用下流過節流孔產生阻尼效應，通過調整節流孔開度，可將阻尼控制在合適的范圍，提高吸振效果。

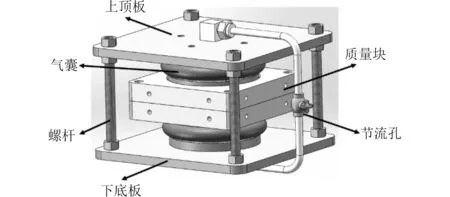
圖1 氣囊式可調頻動力吸振器結構Fig. 1 Structure of the frequency adjustable air-spring dynamic vibration absorber

2 理論模型

2.1 氣室模型

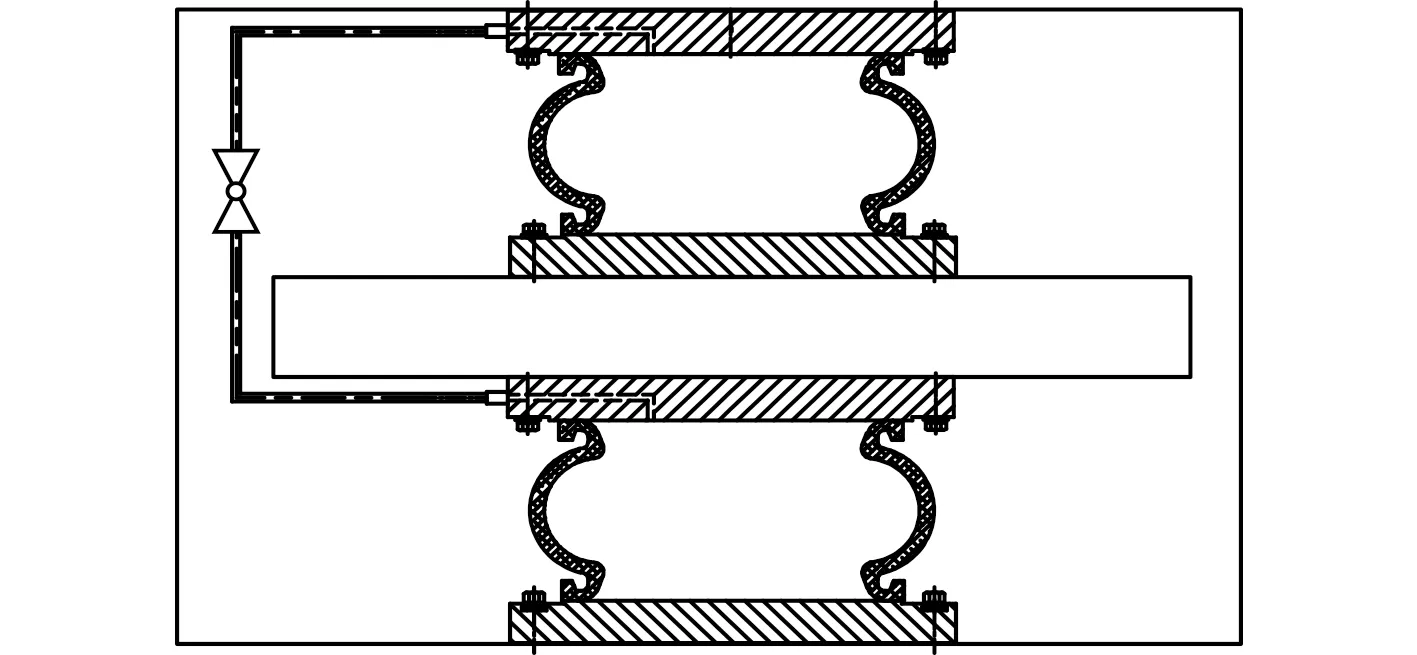
圖2 氣囊式可調頻動力吸振器簡化模型Fig. 2 Simplified model of the frequency adjustable air-spring dynamic vibration absorber

圖3 氣囊式可調頻動力吸振器原理圖Fig. 3 Schematic of the frequency adjustable air-spring dynamic vibration absorber

氣囊式可調頻動力吸振器簡化理論模型如圖3所示，上、下氣囊可視作并聯的剛度元件，K(ω,A)為下方氣室復剛度，K(ω,A)為上方氣室復剛度，忽略氣囊囊體剛度，系統的的總復剛度可以用“氣囊-節流孔-氣囊”模型復剛度表示，即上、下氣室的復剛度之和，其表達式為：

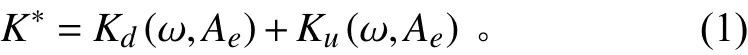
首先對下方氣室進行分析，如圖4所示，根據剛度定義得到其剛度表達式：

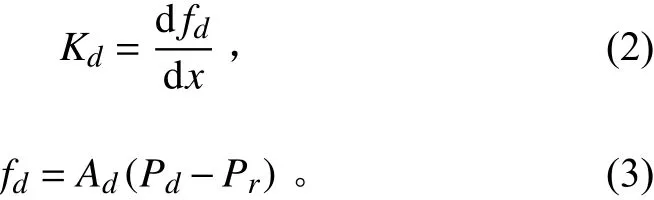
式中：A為下方氣室有效面積，f為下方氣囊垂向負載，為氣囊位移，P為下方氣室絕對壓強，P為環境大氣壓強。

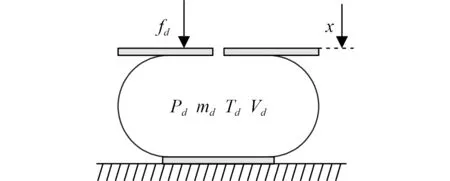
圖4 下方氣囊模型Fig. 4 The model of the lower air spring

假設下方氣囊做微幅振動，則其有效面積A近似為定值，可以得到：

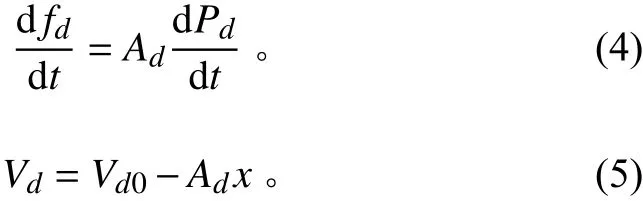
式中：V為下方氣室體積，角標0代表其為初始值。

結合式（1）～式（6），可以得到下方氣室剛度表達式：

假設工作氣體為理想氣體，根據理想氣體狀態方程，可以得到下方氣室氣體質量變化率為：

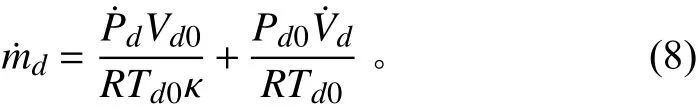
式中：和 κ 為氣體常數和熱力學常數；˙代表下方氣室氣體質量變化率；T，，P表示下方氣室溫度、體積和壓強的初始值。

同理，如圖5所示，可以得到上方氣室氣體質量變化率為：

式中：˙表示上方氣室氣體質量變化率：，，P表示上方氣室溫度、體積和壓強的初始值。A為上方氣室有效面積（近似為定值），f為上方氣囊垂向負載，P為上方氣室絕對壓強。

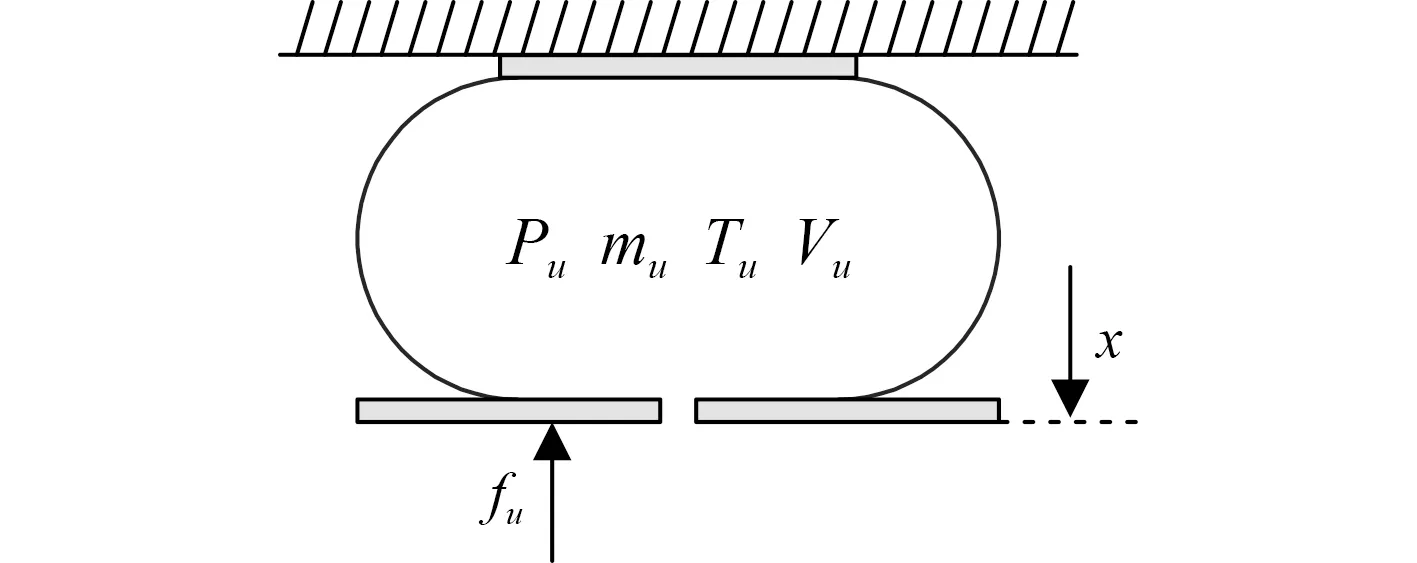
圖5 上方氣囊模型Fig. 5 The model of the upper air spring

2.2 節流孔模型

節流孔的質量流量用˙表示，上、下氣室氣體的總質量不變，可得：

上、下氣囊氣室中的氣體由于壓力差通過節流孔相互流通，如圖6所示，在氣體交換過程中，氣體流動的速度遠遠高于熱量傳遞的速度，該過程可以視為絕熱過程處理。根據文獻[14]，流經節流孔的氣體質量流量可以表示為：

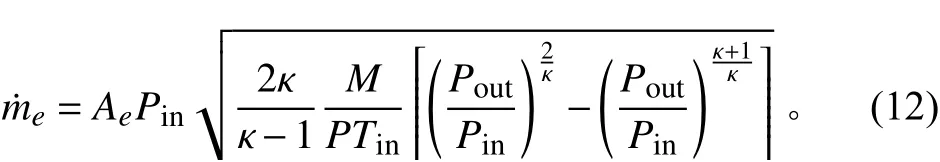
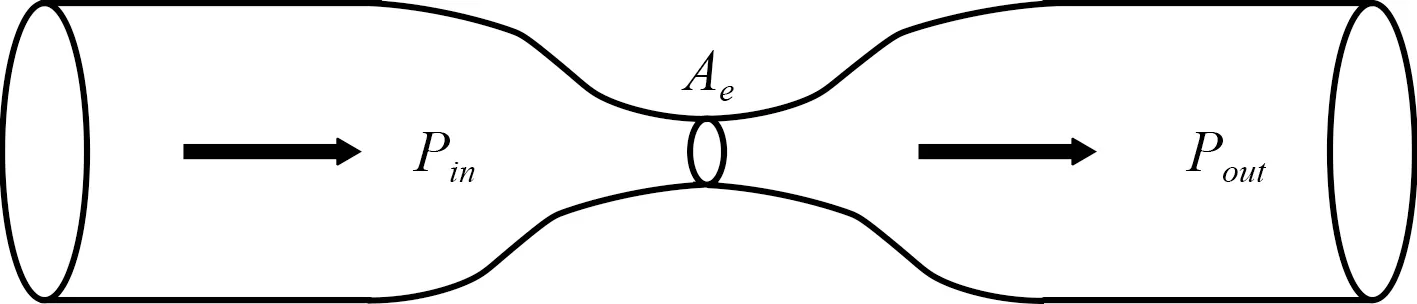
圖6 節流孔模型Fig. 6 The model of orifice

式中：=max(P,P),=min(P,P)，=sign(P-P)T+sign(P-P)T， A為 節流孔截面積，為 氣體摩爾質量。

2.3 復剛度模型

將式（8）和式（9）進行傅里葉變換，得到上、下氣室的頻域質量流量表達式分別為：

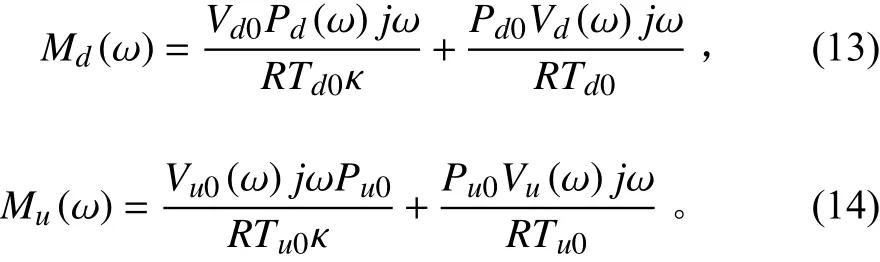
由于氣囊振幅較小，節流孔壓力差只在一個很小的范圍內變化，在平衡點對式（12）進行線性化，得到節流孔頻域質量流量表達式：

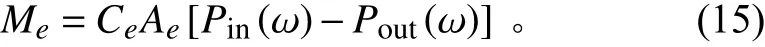
式中：C為 節流孔的流量系數，通過實驗測得。

假設初始狀態上、下氣室同溫同壓，即T=T=， P=P=。將式（13）～式（15）和式（10）～式（11）代入式（7），得到上、下氣室的復剛度分別為：

式中：=V/V，表示下、上氣室初始體積比，式K(ω,A)和K(ω,A)的實部表示系統的儲存剛度，反映系統的剛度特性，虛部表示系統的耗散剛度，反映系統的阻尼特性。

3 復剛度數值計算

以JYQN-30 000型大載荷氣囊為例，其各項參數如表1所示。根據式（16）和式（17），計算“氣囊-節流孔-氣囊”模型復剛度，結果如圖7所示。

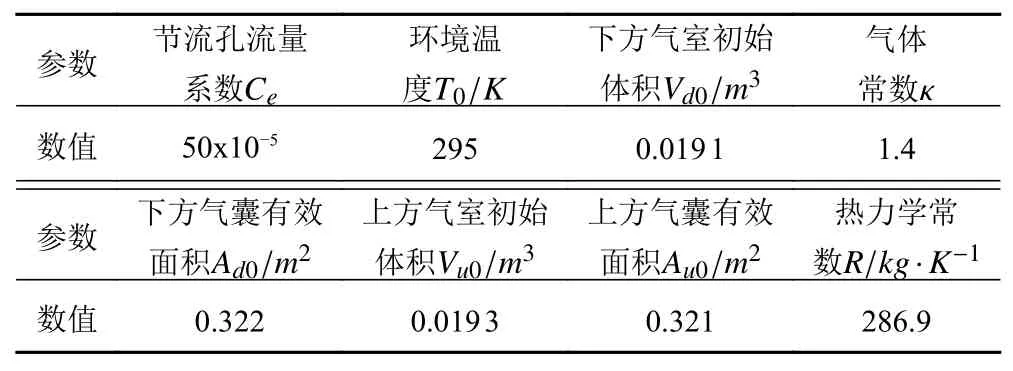
表1 模型參數Tab. 1 Parameters of the model

如圖7（a）和圖7（d）所示，隨著節流孔開度的增大，系統的儲存剛度“S”形曲線逐漸右移，耗散剛度峰值點的頻率變大。圖7（c）和圖7（d）表明，隨著氣囊壓力的升高，系統的儲存剛度在低頻區（0～1 Hz）基本保持不變，在高頻區（12.5～100 Hz）線性增加，耗散剛度整體變大。分析可知，低頻時氣體流速較慢，2個氣囊無障礙相通，導致系統儲存剛度較低，此時無阻尼效應；中頻（1～12.5 Hz）時，在壓力差的作用下，氣體通過節流孔在2個氣囊之間快速流通，形成阻尼效應；高頻時（12.5～40 Hz）氣囊振動較快，氣體在節流孔處形成阻塞，節流孔無氣流通過，2個氣囊處于隔絕狀態，表明節流孔開度和氣囊壓力大小對該系統的儲存剛度和耗散剛度有較大影響。

4 吸振性能分析

4.1 吸振范圍分析

根據計算得到的系統剛度值，求出氣囊不同初始壓力下的吸振器固有頻率，得到不同吸振器質量下的吸振頻率范圍，計算結果如圖8所示。氣囊初始壓力由0.3 MPa變化到2.8 MPa，吸振器質量為0.5 t，1 t和2 t時的固有頻率范圍分別為15.1～46.1 Hz，10.7～32.6 Hz，7.6～23 Hz。

4.2 吸振效果分析

氣囊式可調頻動力吸振器可以通過調節節流孔開度來改善其阻尼特性，提高吸振效果。如圖9所示，對于質量為100 t的主振動系統，吸振器質量為2 t，氣囊式可調頻動力吸振器可通過調整節流孔面積（A=4 cm）達到最優阻尼比=0.08，此時主振動系統的動力放大系數降低為原來的33%，而當阻尼比為0.02（過小）或0.31（過大）時，主振動系統的動力放大系數沒有明顯降低，甚至有所增加。

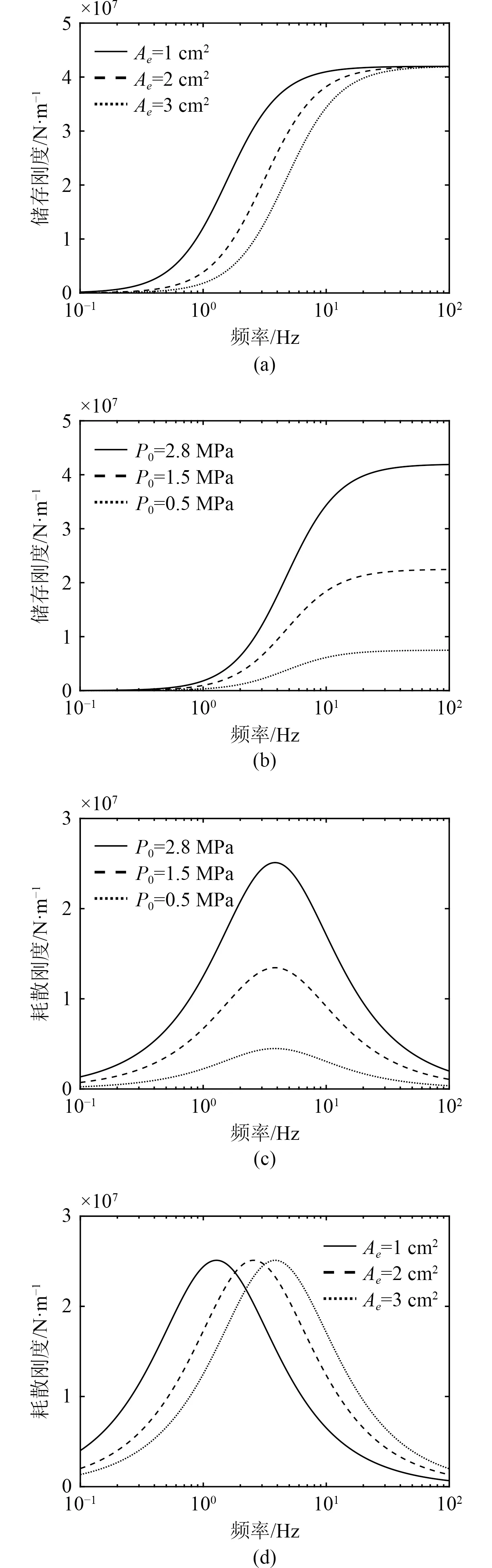
圖7 復剛度計算值Fig. 7 Computational simulation of the complex stiffness

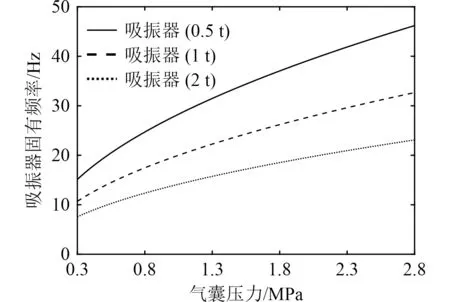
圖8 氣囊式吸振器吸振頻率范圍Fig. 8 Natural frequency range of vibration absorber

圖9 阻尼比對吸振效果的影響Fig. 9 Influence of damping ratio on vibration absorption

吸振器質量是吸振效果的重要影響因素，小質量吸振器無法適用于大型和超大型機械設備。氣囊式可調頻動力吸振器利用氣囊的大載荷特性，可以將吸振器質量調整至2 t，甚至更高，能夠對上百噸的大型機械設備有效吸振。如圖10所示，對于質量為100 t的主系統，當吸振器的質量為2 t時，在主系統固有頻率處，主振動系統的動力放大系數降低為原來的28%。

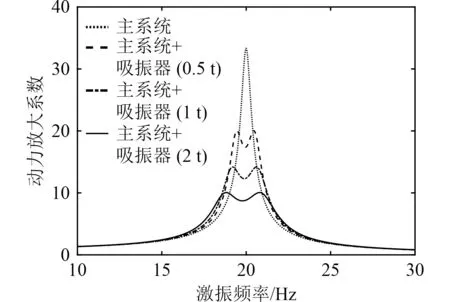
圖10 質量對吸振效果的影響Fig. 10 Influence of mass on vibration absorption

5 結 語

本文首次建立較為完善的“氣囊-節流孔-氣囊”復剛度理論模型，考慮了吸振器剛度和阻尼對吸振效果的影響，通過數值仿真探究不同節流孔開口面積、氣囊氣壓對復剛度的作用，并對該吸振器的吸振范圍、吸振效果進行仿真計算。結果表明，該吸振器對大型設備吸振效果顯著，吸振帶寬可達7.6～46.1 Hz，最高可將主系統振動降低至原來的28%。