半潛式海洋平臺阻力預報數值模擬分析

易 叢，宋春輝，李 剛，陳勇軍，來 敏

(1. 中海油研究總院有限責任公司，北京 100027；2. 北京迪瑪爾海洋技術有限公司，北京 100085)

0 引 言

近年來，半潛式海洋平臺因其良好的穩性、強大的抗風浪能力以及高速的作業效率等優點，在深海工程中發揮著不可或缺的作用。但海洋平臺在海上作業時，受到風、浪、流等環境因素的作用，結構被破壞甚至發生傾覆等海洋事故時有發生，因此海洋平臺阻力預報的準確性對海洋平臺的整體安全性尤為重要。

為了實現海洋平臺阻力的準確預報，國內外學者對平臺阻力計算展開了大量研究。Mataymoto等針對某大水線面立柱半潛平臺提出計算其氣隙響應與分布的完全非線性方法。Li等基于一種新型深水平臺建立平臺主體與立管系統耦合模型，計算了風浪流聯合作用下的平臺的運動響應。范亞麗等針對惡劣海洋環境下的半潛式支持平臺，通過分析試驗來掌握其運動以及阻力特性。張明霞運用STAR-CCM+平臺與OCIMF圖譜插值方法對FPSO在多流向角度下的阻力數值進行計算。董斌等在水池試驗的基礎上利用Ansys-AQWA軟件數值仿真，準確模擬出平臺在自存工況下的阻力。袁洪濤等為了解系泊系統危險工況，對不同風浪流夾角對海洋平臺系泊系統的影響進行研究。陳江華等采用SWAN模型進行不同方向風流浪對平臺穩定性影響的分析，確定平臺危險工況。

現階段，學者對半潛式平臺環境阻力的研究內容主要集中在風速、浪高與平臺本身結構對所受阻力的影響，對不同流向角度下的阻力預報的研究并不多見。因此本文以某半潛式鉆井平臺為研究對象，基于STAR-CCM+平臺對不同流向角度及不同來流速度下的平臺阻力和三維表面壓力進行計算，并分析來流速度和來流方向對阻力及表面壓力的影響，研究結果對平臺設計具有一定指導作用。

1 數值方法

計算流體力學（CFD）是一種基于計算數學、近代流體力學和計算機科學3門學科，通過在計算機上模擬流體流動，實現數值計算與可視化處理，從而達到對所求物理現象能夠較為準確分析研究的方法。STAR-CCM+作為性能優良的CFD軟件，在海洋結構物的水動力和流場模擬方面得到了廣泛應用。

1.1 控制方程

本文數值模擬采用雷諾平均N-S方程，其笛卡爾坐標系下的張量表示形式為:

1.2 湍流模型

CFD軟件中可選擇的湍流模型有-ε 模型，-ω模型，RNG-ε 模型等，本文采用-ε湍流模型。

湍動能方程：

湍流粘性系數方程：

式中：為湍動能，ε為湍流耗散率；Y為可壓速湍流脈動膨脹對總的耗散率的影響；μ為湍流粘性系數；G為平均速度梯度所能引起的湍動能；G為浮力影響所能引起的湍動能。

2 計算模型與邊界條件

2.1 平臺模型

以某半潛式海洋平臺模型為研究對象，其水下部分結構如圖1所示，平臺由2個浮體、立柱以及橫撐等模塊組成，主要結構尺寸如表1所示。

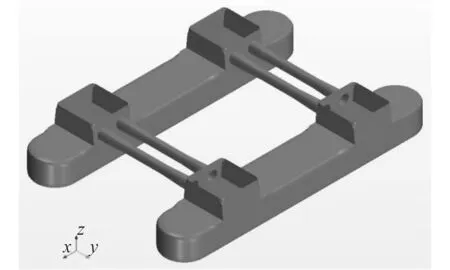
圖1 半潛式平臺水下部分示意圖Fig. 1 Schematic diagram of underwater part of semi submersible platform

表1 平臺模型主要結構尺寸Tab. 1 Main structural dimensions of platform model

2.2 計算域和邊界條件

計算域和邊界條件的設置如圖2所示，計算域為正方體，長寬高分別為4 m×4 m×0.7 m。平臺中心距離速度入口2 m，入口邊界采用Velocity-inlet，出口邊界采用完全發展出流邊界條件Outflow，平臺表面邊界采用無滑移壁面邊界條件，數值計算區域邊界條件設置如圖2所示。

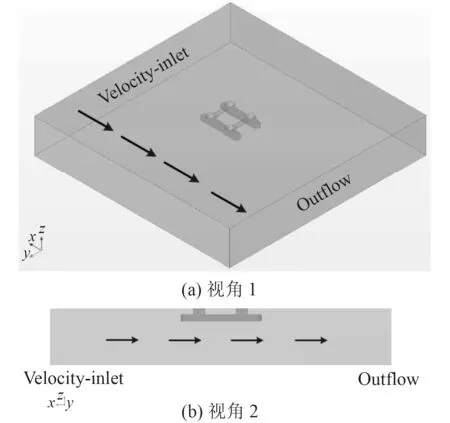
圖2 邊界條件Fig. 2 Boundary conditions

2.3 網格劃分

在劃分網格時，將整個流域劃分為若干區域進行網格劃分，以此提高網格質量和控制網格數量，流場區域的網格劃分如圖3所示。為保證數值模擬精度，全域采用六面體結構化網格，平臺壁面采用精細網格并保證第一層網格位于粘性底層內。半潛式海洋平臺的輪廓特征線進行線控制，同時對平臺表面設置面控制，并做好網格的光滑過渡。網格數約為196.8萬個，半潛式海洋平臺表面網格如圖4所示。

圖3 網格區域網格劃分Fig. 3 Grid division of grid area

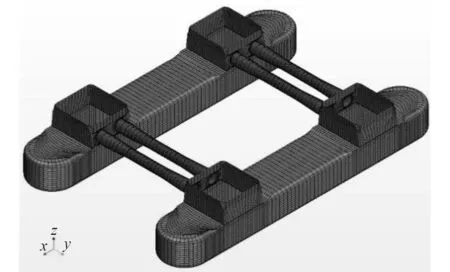
圖4 半潛式海洋平臺網格劃分Fig. 4 Grid division of semi submersible offshore platform

3 計算結果及分析

3.1 模擬精度分析

為驗證本文模擬的精度，對不同來流方向下的平臺總阻力系數與相關試驗結果進行對比，來流速度為1 m/s時對比如圖5所示。可以看出，本文計算結果與試驗值基本吻合，總阻力系數變化規律關于流向角度180°具有一定的對稱性，總阻力系數在流向角度0°～60°時呈現上升趨勢，總阻力系數在流向角度60°～75°時幾乎不變，而75°～90°時總阻力系數略呈現減小趨勢。

計算值與試驗值的誤差范圍如圖6所示，誤差范圍均在3%以內，流向角度為15°，60°以及165°時的誤差值最小，僅為0.06%左右；流向角度為30°及45°時誤差較大為2.53%和2.35%。總體來看，模擬結果在工程允許的誤差范圍內，表明本文方法精確有效。

圖5 不同流向角度下阻力變化曲線對比圖Fig. 5 Comparison of resistance variation curves under different flow direction angles

圖6 誤差范圍Fig. 6 Error range

3.2 不同來流方向平臺表面壓力分析

圖7為來流速度為1 m/s時不同來流方向下平臺表面壓力分布圖，可見受水流撞擊作用的影響，平臺迎流面所受壓力最大，平臺以及立柱和橫撐的背流面的壓力較小，甚至表現為負壓區域。當流向角度增大時，處于下游方向立柱所受阻力越來越小，這是由于隨著流向角度增大，上游迎流方向立柱的尾流“屏蔽區”越來越大。當流向角度為90°時，“屏蔽區”達到最大，下游方向結構完全處于右側浮體的尾流中，其所受壓力明顯小于上游迎流方向。

3.3 不同來流方向下的流載荷分析

圖8為來流速度為1 m/s時不同流向角度下不同方向阻力變化曲線圖。可知，方向阻力變化規律近似于余弦函數，阻力在流向角度0°～60°內減小速度較緩，在流向角度60°～90°內減小速度較快。

方向阻力變化規律近似正弦函數，阻力在流向角度0°～60°內增長速度較快，在流向角度60°～90°內增長速度較慢，當流向角度為60°時，方向阻力最大為50.38 N。方向阻力變化規律關于流向角度180°具有一定的對稱性，且均為負壓，這是由于平臺在一定流向角度上迎流面積相似從而導致阻力變化曲線對稱。當流向角度為0°～60°及90°～165°時，阻力隨流向角度的增加而增加，當流向角度為60°～90°及165°～180°時，阻力隨流向角度的增加而減小。

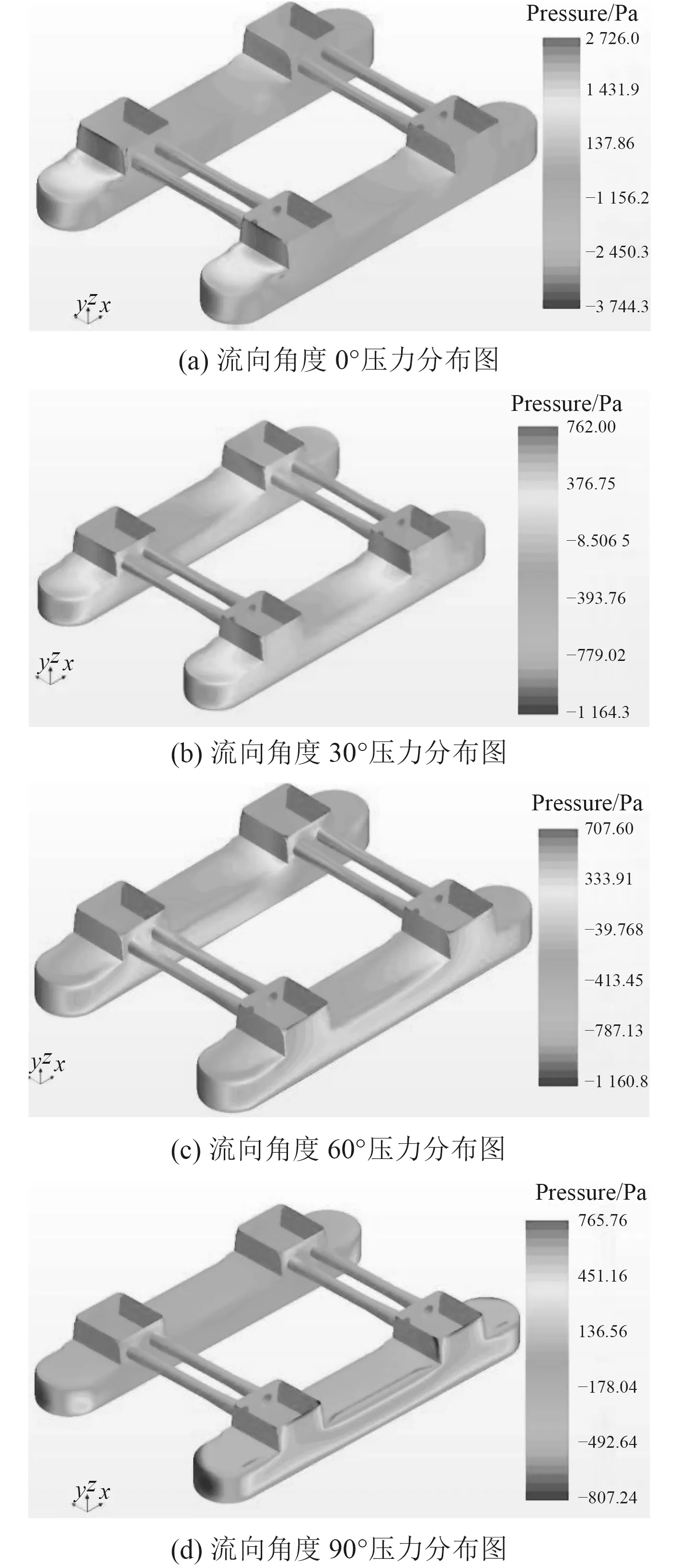
圖7 不同流向角度壓力分布圖Fig. 7 Pressure distribution at different flow directions and angles

圖8 不同流向角度下阻力變化曲線Fig. 8 Resistance variation curve under direction angles

3.4 不同來流速度下的阻力分析

圖9 不同來流速度x方向阻力Fig. 9 x direction at different inflow speeds

圖10 不同來流速度y方向阻力Fig. 10 y direction at different inflow speeds

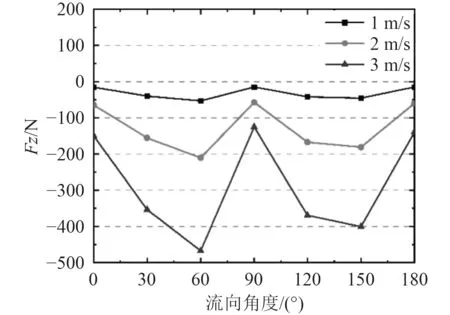
圖11 不同來流速度z方向阻力Fig. 11 x direction at different inflow speeds

圖12 不同來流速度阻力最大值Fig. 12 Max resistance at different velocities

圖9～ 圖11為不同來流速度下xyz方向的阻力，圖12為不同來流速度下阻力最大值。由圖9可知，不同流速下的方向阻力變化規律均近似于余弦函數，方向阻力的值域范圍隨著來流速度的增加而增加。當流向角度為90°時，方向阻力值均為0。由圖10和圖11可知，不同流速下的方向、方向阻力變化規律關于流向角度90°近似對稱，流速越大，阻力越大。由圖12可知，方向和方向的阻力最大值近似相等。

4 結 語

基于STAR-CCM+平臺對不同流向角度及不同來流速度下的平臺阻力和三維表面壓力進行計算，并分析來流速度和來流方向對阻力及表面壓力的影響。主要結論如下：

1）本文基于CFD數值模擬方法進行的數值分析有效，對半潛式海洋平臺的阻力分析具有一定的參考價值；

2）-ε湍流模型對半潛式海洋平臺阻力的預報偏差在2.6%以內；

3）半潛式平臺所受阻力受“遮蔽”效應和迎流面面積的影響；

4）相同來流速度下，各方位阻力隨流向角度增大規律各不相同；

5）相同流向角度下，阻力隨著來流速度的增大而增大。