基于干擾觀測器的X舵AUV零縱傾變深控制

李 楊，韓俊慶，繆旭弘，徐雪峰

(1. 海軍研究院，北京 100161；2. 天津航海儀器研究所九江分部，天津 300131)

0 引 言

自主水下航行器（AUV）相比于其他類型的水下平臺，具有活動范圍大、機動性好、安全、智能化等優點，在海底鋪管、海底勘測、水下設備維修與維護等方面得到了廣泛的應用。如今隨著AUV執行任務的復雜度越來越高，對AUV的操縱性能要求也越來越高。相比于十字舵，X舵具有更高的操縱性，并且具有橫滾控制能力，是未來AUV尾舵的發展趨勢。

然而，由于X舵特殊的布置方式，每個舵面都具有縱傾與航向的控制功能，相比于十字舵，X舵的控制方式不直觀，AUV在進行變深控制時，很難兼顧水平面運動以及保證AUV以小縱傾方式平穩變深，因此研究一種有效的X舵AUV零縱傾變深操縱控制方法尤為重要。

目前，對于變深控制的大部分研究工作都是針對十字尾舵的AUV。楊德成等針對AUV在舵角與舵速約束下的深度控制問題提出一種基于模型預測控制的AUV深度控制方法，仿真結果表明該方法具有良好的動態控制性能。霍江航等針對AUV運動過程中水動力參數攝動與外界干擾問題，基于L1自適應理論提出一種AUV深度控制器，仿真結果表明該控制器擁有良好動態響應的同時能夠保證抗干擾能力與魯棒性。繞志榮等針對AUV在外部擾動與內部擾動下深度難以控制的問題，提出一種基于干擾觀測器的自適應終端滑模控制方法，仿真結果表明此方法有著很強的抗干擾性。

本文根據十字舵AUV深度控制器的設計思路，提出一種X舵AUV的變深控制方法。該方法利用非線性干擾觀測器來補償深度與縱傾通道的耦合干擾與未建模動態，并設計深度與縱傾雙通道耦合控制器，使首舵與尾舵聯合控制深度與縱傾，提高深度與縱傾的控制精度，達到零縱傾變深的目的。設計X舵舵角分配算法，將尾舵指令分配到4個舵角上。仿真實驗驗證了該算法的有效性。

1 模型描述

由于AUV垂直面的運動與水平面的運動之前耦合作用很小，在研究變深控制問題時可忽略水平面運動，因此在AUV六自由度標準模型基礎上進行簡化，得到AUV垂直面的非線性動力學模型如下：

式中：，，，θ分別為AUV的垂向速度、縱傾角速度、深度和縱傾角；為AUV的縱向速度，變深航行時一般保持縱向速度不變；δ為AUV的首舵舵角，δ為AUV的虛擬尾舵舵角，可由X舵的4個舵角轉化得到；d與d為AUV變深運動時垂向與縱傾通道的耦合干擾與未建模動態，其余參數項的表達式如下：

式中，各個動力學系數分別為：

式中：為AUV的浮力，為 AUV質量，為AUV長度，ρ為海水密度，其余參數為水動力參數。

2 控制器設計

本文的控制器設計分為3個部分：1）設計非線性干擾觀測器，估計并補償變深時深度與縱傾通道的耦合干擾與未建模動態；2）設計雙通道耦合滑模控制器，實現AUV的零縱傾高精度變深控制，并引入飽和函數來替代符號函數，消除滑模控制的抖振問題；3）設計X舵舵角分配率，將尾舵指令分配到X舵的4個舵上。控制器的結構形式如圖1所示。

圖1 控制器結構框圖Fig. 1 Block diagram of controller

2.1 非線性干擾觀測器設計

AUV在變深航行過程中，為了保持艇內人員的舒適性，縱傾角一般很小。因此可將式(1)轉化為：

式中，f=-+f。

為了補償AUV變深過程中深度與縱傾通道的耦合干擾與未建模動態，設計深度與縱傾通道的非線性干擾觀測器如下式：

以深度通道為例，證明干擾觀測器的收斂性。定義觀測器誤差?=d-?，考慮到AUV的變深航行是一個大慣性的慢過程，因此假設變深過程中觀測器誤差變化率?=0，則觀測器誤差導數為：

同理也可證得縱傾通道的非線性干擾觀測器收斂。

2.2 滑模控制器設計

從式(3)可以看出，首舵與尾舵同時控制AUV的深度與縱傾。為了簡化控制器設計，設計2個虛擬控制量對深度與縱傾通道進行解耦，2個虛擬量的表達式如下：

則式(3)可轉化為：

以深度通道為例，定義深度與深度變化率的誤差為：

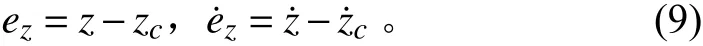
式中，z˙與z為深度與深度變化率指令。

定義線性滑模面為：

式中：c為可調參數，滿足c＞0。

對式(10)求導得：

使˙s=0可得出滑模控制的等效控制率為：

在滑模趨近率方面本文選擇指數型趨近率作為切換控制率：

式中：，k為 滑模趨近率的參數，均為正常數；sgn(·)為符號函數。

因此滑模控制器最終的控制率形式為：

可以看出，由于控制率(14)中符號函數的存在，控制輸出不連續，這便是滑模控制會出現控制器輸出抖振的原因。為了消除抖振，這里引入飽和函數來替代符號函數：

式中：Δ＞0為飽和函數的邊界層厚度，則式(14)可轉化為：

同理可得到縱傾通道控制率為：

2.3 舵角分配算法設計

在控制器解算出虛擬尾舵舵角指令后，下一步將把虛擬尾舵舵角指令分配到X舵的4個舵角上，X舵4個舵的編號如圖2所示。

圖2 X舵布局Fig. 2 Layout of the X-rudder

參考文獻[8]，X舵角與十字舵角的轉換關系為：

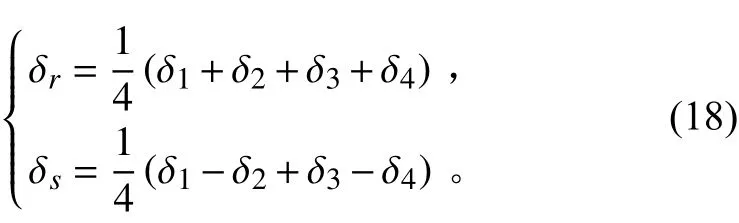
將式(18)轉化為如下形式：

式中： τ=[δ,δ]， τ=[δ,δ,δ,δ]，控制效率矩陣為：

使用偽逆法設計X舵角分配算法，其表達式如下：

3 仿真驗證

基于X舵六自由度操縱運動模型為被控對象，采用文獻[9]的AUV模型參數，對控制器進行驗證。為體現本文算法的控制性能，將其與PID算法的仿真結果進行對比。仿真條件為：AUV初始深度為30 m，航行速度為8 kn，目標深度為60 m；變深控制時不關注水平面的運動，因此在舵角分配時設置方向舵虛擬舵角為0，即 δ=0。仿真結果如圖3～圖9所示，其中NDO-SMC表示本文算法。

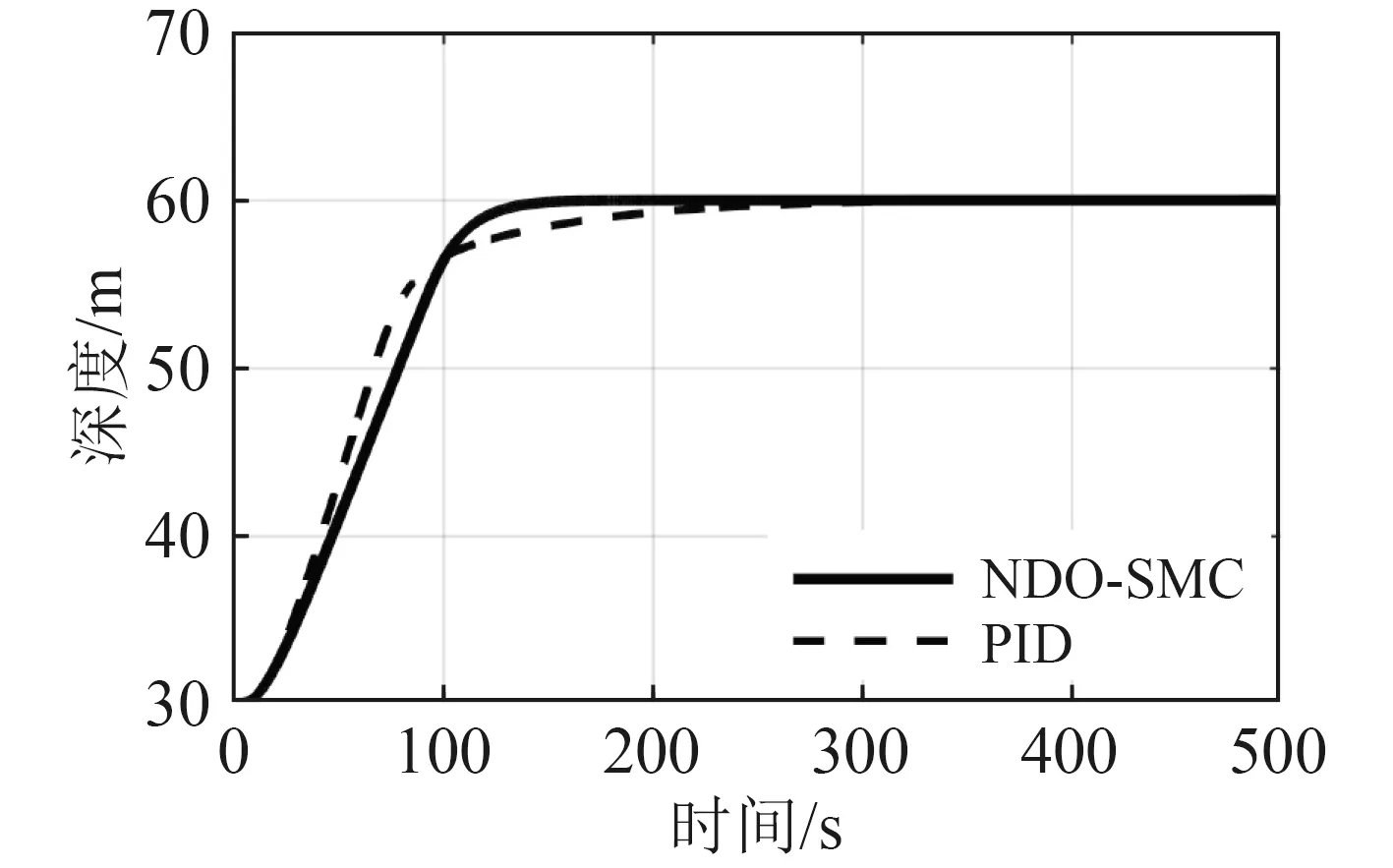
圖3 深度響應曲線Fig. 3 The response curve of depth

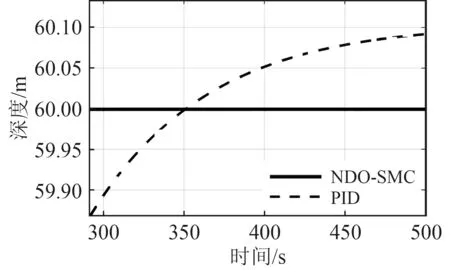
圖4 深度曲線局部放大圖Fig. 4 The detail view of depth curve

圖5 縱傾響應曲線Fig. 5 The response curve of pitch

圖6 舵角1響應曲線Fig. 6 The response curve of rudder 1

圖7 舵角2響應曲線Fig. 7 The response curve of rudder 2

圖8 舵角3響應曲線Fig. 8 The response curve of rudder 3

可以看出，2種控制算法均能夠使X舵AUV完成變深控制，證明了本文所設計舵角分配算法的有效性。

從圖3可以看出，PID控制器在初期有很快的響應速度，在90 s左右收斂速度放緩，而NDO-SMC控制器雖然在初期響應速度不如PID，但在150 s左右已收斂到指定深度，因此相比與PID控制器，NDO-SMC控制器深度收斂速度更快；從圖4中的深度曲線局部放大圖可以明顯看出，相比與相比與PID控制器，NDOSMC控制器有著更高的深度控制精度。

圖9 舵角4響應曲線Fig. 9 The response curve of rudder 4

從圖5的縱傾響應曲線可以看出，NDO-SMC控制器使縱傾角在100 s左右收斂到0，調節過程中最大縱傾角為-0.25°，整個過程幾乎保持零縱傾變深，而PID控制器使AUV在變深時最大產生了-1.7°的縱傾角，且縱傾收斂速度較慢，因此相比PID控制器，NDO-SMC控制器有著更強的縱傾控制能力。

從圖6～圖10的舵角響應曲線可以看出，相比PID控制器，NDO-SMC控制器的動舵幅度更大，舵利用率更高，更好地發揮了操舵系統的控制性能。

圖10 首舵響應曲線Fig. 10 The response curve of bow rudder

4 結 語

本文針對X舵AUV的零縱傾變深控制問題，設計一種基于非線性干擾觀測器的滑模控制器，并采用偽逆法將控制器產生的舵角指令分配到X舵的4個舵角。仿真結果表明，相比PID控制器，本文控制器能夠有效地提高變深控制中深度與縱傾的控制精度與收斂速度，能夠有效控制X舵型AUV零縱傾平穩變深航行。