非正弦升沉運(yùn)動(dòng)下串列水翼推進(jìn)性能研究

李光釗，常 欣，鄧南彥，于鵬垚

(大連海事大學(xué) 船舶與海洋工程學(xué)院，遼寧 大連 116026)

0 引 言

在自然界中，蜻蜓、蜜蜂等昆蟲(chóng)的撲翼結(jié)構(gòu)是最常見(jiàn)的串列撲翼系統(tǒng)，學(xué)者們從中獲得靈感，采用多翼串列的方式來(lái)提升撲翼系統(tǒng)的推進(jìn)性能。于憲釗等分析了前翼拍動(dòng)后翼靜止的串列翼系統(tǒng)水動(dòng)力；Jones等分析了串列水翼的推進(jìn)性能并進(jìn)行了相關(guān)試驗(yàn)研究；Broering等采用數(shù)值模擬方法研究了串列撲翼的氣動(dòng)力性能；石成明等采用氣動(dòng)力試驗(yàn)方法研究了串列翼型所產(chǎn)生的推力與前后翼距離之間的變化規(guī)律；李永澤等研究了3種串列雙翼的氣動(dòng)布局，分析了最優(yōu)的前后翼布局方案。許國(guó)冬等針對(duì)典型推進(jìn)運(yùn)動(dòng)模式與能量采集模式，分析了串列雙翼之間渦的干擾規(guī)律。

盡管國(guó)內(nèi)外針對(duì)串列翼的氣動(dòng)力和水動(dòng)力性能已開(kāi)展許多研究，但過(guò)往研究中的串列翼運(yùn)動(dòng)形式大多為正弦運(yùn)動(dòng)。自然界生物的撲翼運(yùn)動(dòng)軌跡往往是更為復(fù)雜的非正弦運(yùn)動(dòng)，目前尚未看到針對(duì)非正弦運(yùn)動(dòng)串列水翼推進(jìn)表現(xiàn)的研究。在串列撲翼式水下航行器的研發(fā)驅(qū)動(dòng)下，本文采用計(jì)算流體力學(xué)方法研究非正弦升沉運(yùn)動(dòng)下串列水翼的推進(jìn)性能，為水下航行器的撲翼運(yùn)動(dòng)模式選擇提供指導(dǎo)。

1 計(jì)算方法

1.1 撲翼運(yùn)動(dòng)的描述

本文中非正弦運(yùn)動(dòng)通過(guò)橢圓形軌跡實(shí)現(xiàn)，其中，撲翼的升沉運(yùn)動(dòng)位移方程定義如下：

其中：為撲翼升沉運(yùn)動(dòng)的非正弦參數(shù)；為升沉運(yùn)動(dòng)幅值； ω=2π，為拍動(dòng)頻率；為時(shí)間。=1時(shí)，撲翼運(yùn)動(dòng)即為正弦運(yùn)動(dòng)，不同值對(duì)應(yīng)的撲翼運(yùn)動(dòng)軌跡如圖1所示。

圖1 不同S值的撲翼運(yùn)動(dòng)軌跡Fig. 1 Flapping trajectories according to different values of S

當(dāng)兩撲翼前后串列排布時(shí)，前翼和后翼的升沉運(yùn)動(dòng)可分別表示為：

其中：()為串列排布兩翼中前翼的運(yùn)動(dòng)方程，()為后翼的運(yùn)動(dòng)方程；為撲翼升沉運(yùn)動(dòng)非正弦參數(shù)；為前后兩翼升沉運(yùn)動(dòng)的相位差。

圖2 串列水翼布置圖Fig. 2 Layout of in-line tandem hydrofoils

1.2 物理量的定義

撲翼在運(yùn)動(dòng)時(shí)會(huì)受到不同方向上的水動(dòng)力和水動(dòng)力矩。本文對(duì)串列翼系統(tǒng)的前后水翼力學(xué)特性分別討論，作用在單獨(dú)進(jìn)行升沉運(yùn)動(dòng)水翼上的瞬時(shí)推力系數(shù)C和瞬時(shí)升力系數(shù)C可表達(dá)為：

其中：F()為作用在單獨(dú)水翼上沿軸的瞬時(shí)推力；F()為作用在單獨(dú)水翼上沿軸的瞬時(shí)升力；為流體的密度；為流場(chǎng)來(lái)流速度。

則平均推力系數(shù)C和平均功率系數(shù)C可表達(dá)為：

其中：為撲翼升沉運(yùn)動(dòng)周期；P為撲翼運(yùn)動(dòng)時(shí)所需功率。

對(duì)于升沉運(yùn)動(dòng)水翼，一個(gè)運(yùn)動(dòng)周期所需的功率可以通過(guò)下式計(jì)算：

其中：為水翼沿軸軸向速度。

單獨(dú)水翼的推進(jìn)效率 η可表達(dá)為：

1.3 數(shù)值方法與計(jì)算模型

本文采用基于有限體積法的商用CFD求解器STAR-CCM+進(jìn)行串列水翼的水動(dòng)力分析。其中，水翼的運(yùn)動(dòng)利用重疊網(wǎng)格技術(shù)來(lái)實(shí)現(xiàn)。數(shù)值模型的計(jì)算域如圖3所示，其中，分析的水翼為NACA0012標(biāo)準(zhǔn)翼型，翼弦長(zhǎng)=0.1 m。方形區(qū)域?yàn)楸尘坝颍叽缭O(shè)置為70×70；中間圓形區(qū)域?yàn)橹丿B域，半徑為1。根據(jù)Chao等的研究，當(dāng)撲翼和計(jì)算域邊界的距離大于20時(shí)，流域尺寸對(duì)水翼水動(dòng)力的影響可以忽略不計(jì)，因此，可以判斷本文中的計(jì)算域尺寸已足夠大。具體的計(jì)算域邊界條件如圖3所示。

圖3 串列雙翼計(jì)算域及邊界條件Fig. 3 The domain and boundary conditions of in-line tandem hydrofoils

1.4 數(shù)值收斂性分析

性分析，具體計(jì)算參數(shù)取值為=0.7，=1×10，=0.35 ，=0.25 ，相 位 差 ε=0 。其 中，為雷諾數(shù)，其定義為：

針對(duì)數(shù)值模型中的時(shí)間步長(zhǎng)和網(wǎng)格尺寸進(jìn)行收斂

式中：為來(lái)流速度，為水的動(dòng)力粘度。為斯特勞哈爾數(shù)，反映流體非定常運(yùn)動(dòng)的相似性，其定義為：

式中，為運(yùn)動(dòng)頻率。

圖4 不同時(shí)間步長(zhǎng)下瞬時(shí)推力系數(shù)時(shí)歷曲線Fig. 4 Time history of instantaneous thrust coefficient of in-line tandem flapping foil under different time steps

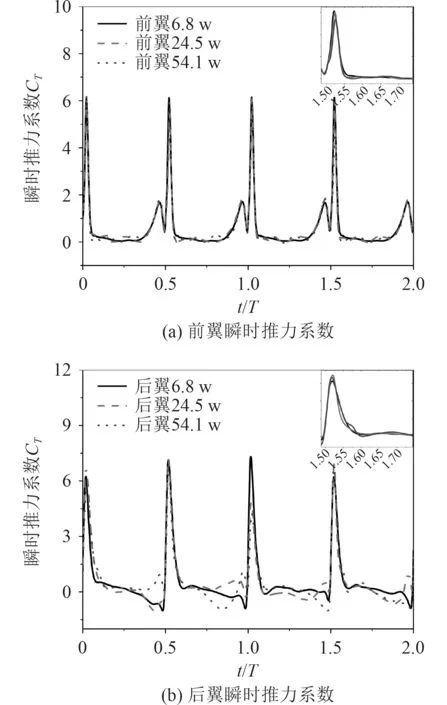
圖5 不同網(wǎng)格下的瞬時(shí)推力系數(shù)時(shí)歷曲線Fig. 5 Time history of instantaneous thrust coefficient of in-line tandem flapping foil under different grids

圖4為不同時(shí)間步長(zhǎng)下前后水翼推力系數(shù)時(shí)歷曲線的比較。計(jì)算中選取的時(shí)間步長(zhǎng)分別為d=/1 000，/2 500，/4 000，對(duì)應(yīng)計(jì)算模型的網(wǎng)格數(shù)目為24.5萬(wàn)。可以看出，不同時(shí)間步長(zhǎng)下水翼的推力曲線吻合較好，故時(shí)間步長(zhǎng)d=/2 500用于后續(xù)計(jì)算。圖5為不同網(wǎng)格密度下前后水翼推力系數(shù)時(shí)歷曲線的比較。對(duì)應(yīng)3個(gè)不同的網(wǎng)格密度，撲翼表面分別具有200，400，600個(gè)節(jié)點(diǎn)，對(duì)應(yīng)計(jì)算模型的網(wǎng)格數(shù)目分別為6.8萬(wàn)、24.5萬(wàn)和54.1萬(wàn)，計(jì)算中采用的時(shí)間步長(zhǎng)d=/2 500。可以看出，不同時(shí)間步長(zhǎng)下水翼的推力曲線總體吻合較好，表明當(dāng)前數(shù)值模型具有較好的網(wǎng)格收斂性，在后續(xù)計(jì)算中選取網(wǎng)格數(shù)目為24.5萬(wàn)的計(jì)算模型。

1.5 數(shù)值算法的驗(yàn)證

圖6為本文數(shù)值結(jié)果與Heathcote等試驗(yàn)結(jié)果以及Y.L.Wang等和Young等數(shù)值結(jié)果的對(duì)比。其中，計(jì)算翼型為NACA0012水翼，弦長(zhǎng)=0.1 m，雷諾數(shù)=2×10，運(yùn)動(dòng)幅值=0.175，水翼運(yùn)動(dòng)形式為單翼的正弦純升沉運(yùn)動(dòng)。橫坐標(biāo)為無(wú)量綱所減頻率，定義為=2π/。可以看出，本文數(shù)值結(jié)果與文獻(xiàn)[9]試驗(yàn)結(jié)果吻合較好。圖7為本文數(shù)值結(jié)果與Kinsey等結(jié)果的對(duì)比。其中，文獻(xiàn)中的計(jì)算結(jié)果也被許國(guó)冬等采用，用于驗(yàn)證數(shù)值模型。其中，計(jì)算翼型為NACA0015水翼，弦長(zhǎng)=0.1 m ，雷諾數(shù)=2×10，運(yùn)動(dòng)幅值=1.0，水翼運(yùn)動(dòng)形式為串列水翼的俯仰升沉復(fù)合運(yùn)動(dòng)。可以看出，本文數(shù)值結(jié)果與文獻(xiàn)數(shù)值結(jié)果吻合較好。總體而言，當(dāng)前數(shù)值方法在本文中的應(yīng)用是合理可行的。

圖6 單翼升沉運(yùn)動(dòng)驗(yàn)證Fig. 6 Plunge motion verification of single hydrofoil

圖7 串列雙翼復(fù)合運(yùn)動(dòng)驗(yàn)證Fig. 7 Combined motion verification of in-line tandem hydrofoils

2 結(jié)果與分析

主要討論非正弦運(yùn)動(dòng)對(duì)串列升沉水翼推進(jìn)性能的影響，其中無(wú)特殊說(shuō)明，計(jì)算參數(shù)=0.7，=1×10，=0.35，L=7.5，保持不變。

2.1 非正弦升沉系數(shù)S對(duì)瞬時(shí)水動(dòng)力的影響

采用前后翼相位差 ε=90的結(jié)果進(jìn)行分析。如圖8（a）所示，對(duì)于前翼的瞬時(shí)推力系數(shù)曲線：從峰值來(lái)看，非正弦系數(shù)從=1增大或減小，都會(huì)使前翼瞬時(shí)推力系數(shù)曲線峰值增加；從周期來(lái)看，增大非正弦系數(shù)時(shí)周期基本不變，而減小非正弦系數(shù)時(shí)原有周期發(fā)生變化，峰值出現(xiàn)位置由水翼運(yùn)動(dòng)的平衡位置（0.25、0.75）變化為水翼運(yùn)動(dòng)的極端位置（0、0.5、1）。如圖8（b）所示，對(duì)于后翼的瞬時(shí)推力系數(shù)曲線：從峰值來(lái)看，隨著非正弦系數(shù)的減小，后翼推力系數(shù)曲線峰值增大，隨著非正弦系數(shù)的增大，峰值先減后增；從周期來(lái)看，由于相位差的存在，后翼周期應(yīng)比前翼推遲0.25，而當(dāng)=1時(shí)，峰值卻提前出現(xiàn)，這是前翼的尾流作用所致。

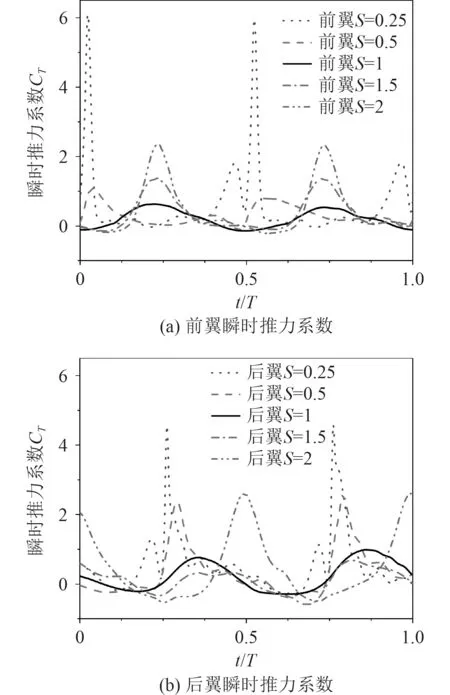
圖8 不同非正弦系數(shù)下串列撲翼的瞬時(shí)推力系數(shù)時(shí)歷Fig. 8 Time history of instantaneous thrust coefficients of in-line tandem flapping foils under different non-sinusoidal coefficient

圖9 不同非正弦系數(shù)下串列撲翼的瞬時(shí)升力系數(shù)時(shí)歷Fig. 9 Time history of instantaneous lift coefficients of in-line tandem flapping foils under different non-sinusoidal coefficient

如圖9（a）所示，對(duì)于前翼的升力系數(shù)曲線：從峰值和谷值來(lái)看，從=1增大或減少非正弦系數(shù)均可增大或減小升力系數(shù)曲線的峰值或谷值，且從=1減小時(shí)相比于增大時(shí)峰值增大或谷值減小的程度更大；從周期來(lái)看，當(dāng)＞1時(shí)周期基本不變，而當(dāng)＜1時(shí)，峰值或谷值出現(xiàn)位置由水翼運(yùn)動(dòng)的平衡位置（0.25、0.75）變化為水翼運(yùn)動(dòng)的極端位置（0、0.5、1）。如圖9（b）所示，對(duì)于后翼的瞬時(shí)升力系數(shù)曲線：從峰值和谷值來(lái)看，從=1增大或減小非正弦系數(shù)同樣會(huì)使升力系數(shù)曲線峰值更大，谷值更小；從周期來(lái)看，由于相位差的存在，后翼的周期性變化比前翼慢0.25。

2.2 非正弦升沉系數(shù)S對(duì)渦結(jié)構(gòu)的影響

圖10和圖11分別為前后兩翼在=0.5時(shí)刻不同非正弦升沉運(yùn)動(dòng)時(shí)周圍流場(chǎng)的渦量云圖。此時(shí)前翼處于最大負(fù)向位移位置，后翼處于向下運(yùn)動(dòng)的平衡位置。將水翼的上表面稱為吸力面，下表面稱為壓力面，水翼形成升力的原因是吸力面與壓力面的壓強(qiáng)差。

前翼在非正弦系數(shù)=1時(shí)，一組尾渦由2個(gè)正向旋轉(zhuǎn)、1個(gè)負(fù)向旋轉(zhuǎn)的渦組成。在脫落過(guò)程中，正向旋轉(zhuǎn)的渦迅速變?nèi)踔料АＫ硎撞坑幸粚?duì)旋向相反的渦，且?guī)е粋€(gè)未與水翼表面接觸的負(fù)向旋渦。當(dāng)這組渦向水翼尾部運(yùn)動(dòng)時(shí)，渦強(qiáng)度逐漸減弱。由于上表面的渦弱，上下表面壓力差不大，升力無(wú)明顯變化。當(dāng)＜1時(shí)，尾渦組成與=1時(shí)相似，當(dāng)減小時(shí)，尾渦中一個(gè)正向旋轉(zhuǎn)的渦強(qiáng)度增強(qiáng)，推力明顯增大。當(dāng)＞1時(shí)，一組尾渦由2對(duì)旋向相反的渦組成，且脫落后負(fù)向旋渦迅速減弱，當(dāng)增大時(shí)，上表面脫落的負(fù)向旋渦強(qiáng)度增大。

圖10 前翼運(yùn)動(dòng)至最大負(fù)向位移位置處(t=0.5T)的渦量云圖Fig. 10 The vorticity contour of the forefoil moving to the position of maximum negative displacement (t=0.5T)

圖11 后翼運(yùn)動(dòng)至平衡位置處（t=0.5T）的渦量云圖Fig. 11 The vorticity contour of the hindfoil moving to the equilibrium position (t=0.5T)

對(duì)于后翼在非正弦系數(shù)=1時(shí)，有一個(gè)負(fù)向旋渦在首端脫落，有一個(gè)正向旋渦在尾端脫落。負(fù)向旋渦比正向旋渦強(qiáng)度更強(qiáng)，有一組旋向相反的渦在尾流中，觀察到有前翼的尾渦運(yùn)動(dòng)到后翼附近。當(dāng)＜1時(shí)，首端負(fù)向旋渦分為2個(gè)，尾端正向旋渦和尾渦中的負(fù)向旋渦隨的減小而減弱。當(dāng)＞1時(shí)，隨著的增大，尾端的正向旋渦強(qiáng)度增強(qiáng)，首端負(fù)向旋渦強(qiáng)度減弱。

2.3 非正弦升沉系數(shù)S對(duì)推進(jìn)表現(xiàn)的影響

從圖12（a）可知，對(duì)于前翼，從非正弦系數(shù)=1增大或減少，均能增加前翼的平均推力系數(shù)。在=0.5時(shí)前翼平均推力系數(shù)在相位差為90°處變化明顯，在此非正弦系數(shù)下，后翼對(duì)前翼的推力影響較大。從圖12（b）可知：在大多數(shù)相位差下，從=1增大或減小非正弦系數(shù)可以增強(qiáng)后翼平均推力系數(shù)，但在某些相位差下，非正弦運(yùn)動(dòng)的平均推力系數(shù)小于正弦運(yùn)動(dòng)的平均推力系數(shù)。如相位差為0時(shí)，=0.5的平均推力系數(shù)小于=1的平均推力系數(shù)。總體來(lái)看，隨著相位差的增加，平均推力系數(shù)先增后減。

從圖12（c）可知，對(duì)于前翼的推進(jìn)效率，當(dāng)＞1時(shí)，推進(jìn)效率隨的增大而減小，當(dāng)＜1，推進(jìn)效率隨的減小而增大。可以觀察到在=0.5時(shí)，前翼推進(jìn)效率曲線在不同的相位差下，數(shù)值發(fā)生較明顯變化，推測(cè)是此非正弦系數(shù)和相位差時(shí)后翼對(duì)前翼的影響較大所致。從圖12（d）可知，對(duì)于后翼的推進(jìn)效率同樣在＞1時(shí)，推進(jìn)效率隨的增大而減小，隨相位差的增大先減后增，在＜1時(shí)，隨的減小而增大，隨相位差的增大先增后減。

圖12 前后翼在不同相位差下，撲翼推進(jìn)表現(xiàn)隨非正弦系數(shù)的變化Fig. 12 Under different phase differences, the propulsion performance of the fore and hind foils changes with the non-sinusoidal coefficient

3 結(jié) 語(yǔ)

本文采用計(jì)算流體力學(xué)方法和重疊網(wǎng)格技術(shù)研究了非正弦運(yùn)動(dòng)對(duì)串列升沉水翼推進(jìn)性能的影響，得到如下結(jié)論：

1）通過(guò)不同時(shí)間步長(zhǎng)和網(wǎng)格尺寸的數(shù)值結(jié)果比較，驗(yàn)證了數(shù)值模型的收斂性；通過(guò)與公開(kāi)發(fā)表試驗(yàn)和數(shù)值結(jié)果的比較，驗(yàn)證了數(shù)值模型的計(jì)算精度。

2）非正弦升沉運(yùn)動(dòng)相比于正弦升沉運(yùn)動(dòng)會(huì)增大撲翼的瞬時(shí)推力峰值和升力峰值，而且，非正弦系數(shù)的量值與1的偏差越大，瞬時(shí)峰值增大程度越明顯。

3）非正弦系數(shù)可以改變水翼表面渦的脫落模式，當(dāng)＜1時(shí)，一組尾渦由2個(gè)旋向相同、一個(gè)旋向相反的渦組成；當(dāng)＞1時(shí)，一組尾渦由2對(duì)旋向相反的渦組成。

4）除個(gè)別少數(shù)相位差對(duì)應(yīng)的運(yùn)動(dòng)狀態(tài)，與正弦運(yùn)動(dòng)相比，當(dāng)非正弦系數(shù)從=1增大或減小時(shí)，非正弦運(yùn)動(dòng)下的前翼和后翼平均推力增大。

5）除個(gè)別少數(shù)相位差對(duì)應(yīng)的運(yùn)動(dòng)狀態(tài)，與正弦運(yùn)動(dòng)相比，當(dāng)非正弦系數(shù)從=1增大時(shí)，前翼和后翼的推進(jìn)效率減小；當(dāng)非正弦系數(shù)從=1減小時(shí)，前翼和后翼的推進(jìn)效率增大。除此之外，在此基礎(chǔ)上改變雙翼相位差可以進(jìn)一步使串列水翼達(dá)到最佳推進(jìn)效率，這將為串列雙翼水下航行器推進(jìn)系統(tǒng)的設(shè)計(jì)提供指導(dǎo)。