漂浮式風力機平臺局部系泊蠕變模式下動態響應分析

孫 康， 金江濤， 李 春,2， 李蜀軍， 許子非， 肖俊青

(1.上海理工大學 能源與動力工程學院，上海 200093；2.上海市動力工程多相流動與傳熱重點實驗室，上海 200093)

隨著人類工業文明迅速發展，能源儲量驟減、環境污染等問題凸顯，因此推進能源轉型、尋找綠色可再生能源已引起世界各國廣泛關注[1]。

風能作為人類最早開發利用的可再生能源，具有儲量豐富、分布廣泛、綠色清潔和開采便利等優點，已成為最具發展前景的可再生能源之一。且隨著風能研究的不斷深入，海上風能因距經濟發展中心近以及輸送損耗低等優點而發展迅速。國家“十四五”規劃綱要[2]明確提出“建設清潔低碳能源體系”、“大力提升風電”和“有序發展海上風電”等要求。但隨著近海活動向深水域發展，樁柱式海上風力機已難以滿足要求，需研發更合適的離岸支撐結構。其中，漂浮式風力機因其適用于深水深、廣海域且施工安裝靈活等優勢而逐漸被風能領域接受并得到大量工程部署[3]。

作為深海風能的主要開發設備，漂浮式風力機因其重心高和無固定基礎，在工作過程中受到風、浪、海流、風力機空氣動力載荷以及風傾力矩等作用，系統各組成部分間耦合效應明顯[4]。為確保風力機不發生位移與傾倒，通過系泊連接海底錨點為其提供定位與回復力。但因平臺浮動特性造成的搖蕩運動使系泊受到較大的時變拉力，同時因海水長期腐蝕與磨損等，影響整個漂浮式風力機系統安全運行，甚至導致平臺損毀、人員傷亡和環境污染等特大災難性事故發生[5]。2005年，颶風Rita造成服役于墨西哥灣的張力腿平臺Typhoon TLP發生筋腱失效事故，最終導致發生傾覆事故[6]。當系泊失效后，漂浮式風力機動力響應增大，威脅其安全運行。

近年來，漂浮式風力機系統存在各種失效風險，平臺動態響應方面的研究逐漸興起。Li等[7]基于OC3-HywindSpar型浮式風力機，研究其在額定海況下出現單根錨鏈失效后的動態響應，發現錨鏈失效的風力機會增加相鄰風力機的碰撞風險。Bae等[8]分析OC4-DeepCwind半潛型浮式風力機發生單根錨鏈失效后的動態響應，結果表明錨鏈失效會造成平臺出現遠距離漂移運動，并對錨鏈張力與機艙偏航誤差具有一定影響。Yang等[9]基于細長桿理論簡化立管與系纜，建立深水浮式結構-系泊系統耦合分析方法，研究各組成部分間的耦合效應。但上述研究大多針對風力機錨鏈失效后的動態響應，有關漂浮式風力機系泊方面的研究很少。

目前，深度學習廣泛應用于風力機葉片故障診斷。其中，卷積神經網絡(Convolutional Neural Network, CNN)因其提取特征能力強與分類效率高等優點逐漸受到重視[10]。Kreutz等[11]通過CNN對風輪葉片上的圖像進行識別，實現對葉片結冰情況的精準識別；Cao等[12]采用CNN學習和提取葉片故障特征，準確檢測出葉片氣動與質量不平衡故障。郭迎福等[13]融合CNN與三維振動信號對葉片裂紋進行診斷，通過建立裂紋樣本數據庫，實現了高精度識別效果。

基于此，筆者以搭載美國國家可再生能源實驗室(National Renewable Energy Laboratory, NREL)5 MW風力機的ITI Energy Barge平臺的系泊系統為研究對象，采用CNN對不同系泊蠕變下的動態響應數據進行分析，充分利用深度學習模型對蠕變系泊的信息進行挖掘，提取純凈信號，并結合混沌理論分析其吸引子軌跡，揭示隱藏于隨機現象中的真實規律[14]。

1 研究對象

1.1 漂浮式風力機模型

以ITI Energy Barge平臺NREL 5 MW漂浮式風力機為研究對象。整機系統如圖1所示[15]。

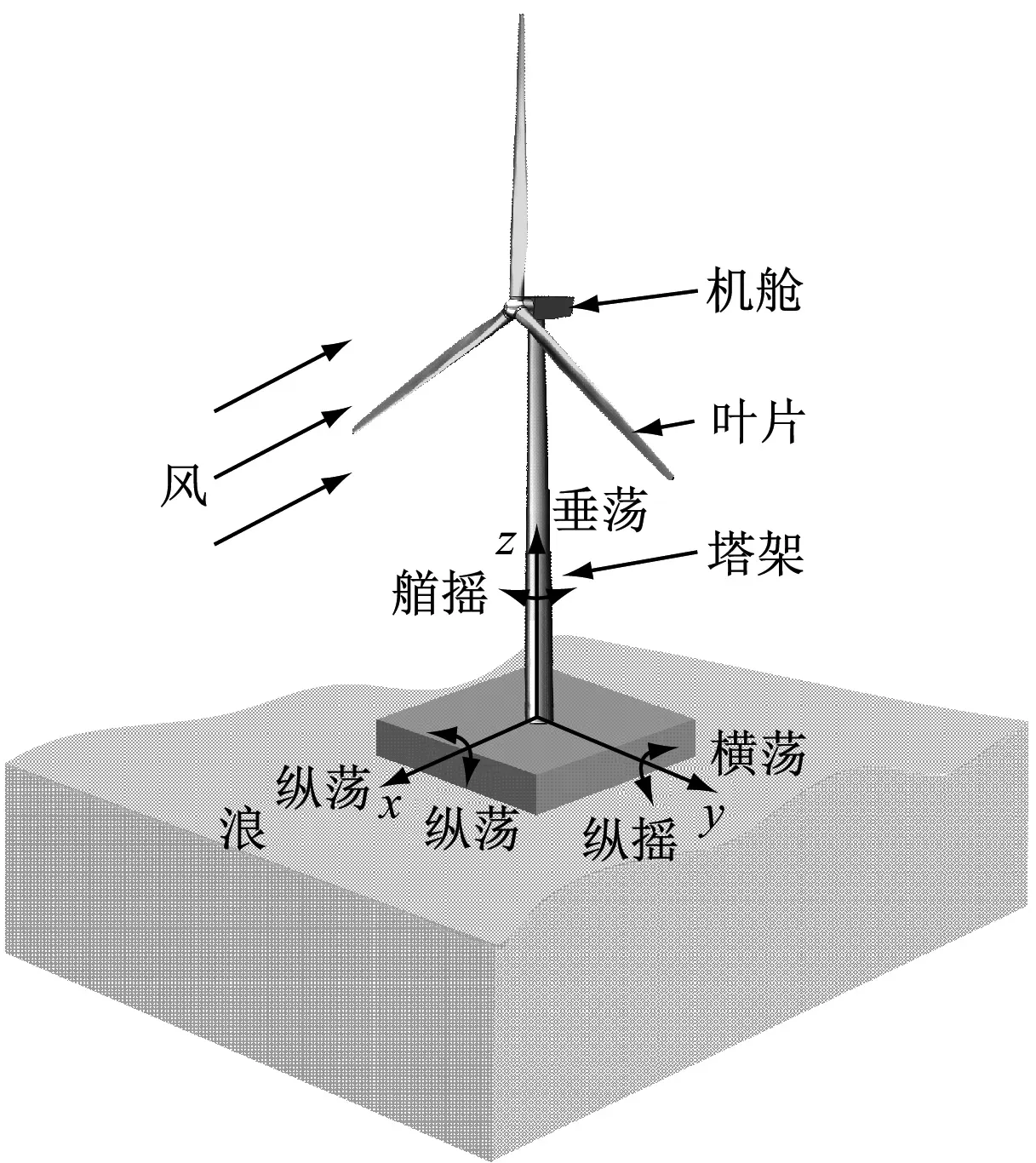
圖1 Barge平臺漂浮式風力機平臺

風力機及漂浮式平臺主要參數見表1和表2。

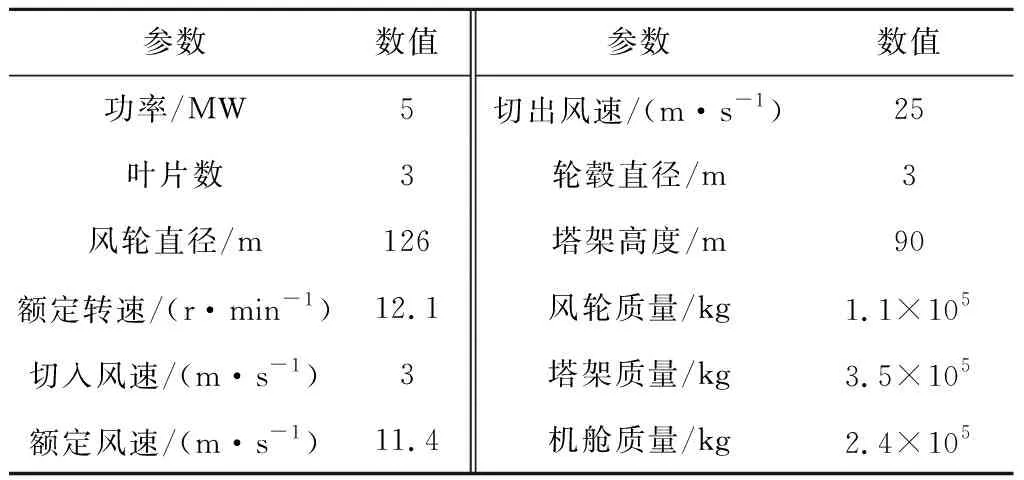
表1 風力機主要參數

1.2 系泊系統

ITI Energy Barge平臺通過4個角上導纜孔的8根系泊與海底錨點連接，平臺俯視圖如圖2所示。系泊參數見表3[16]。

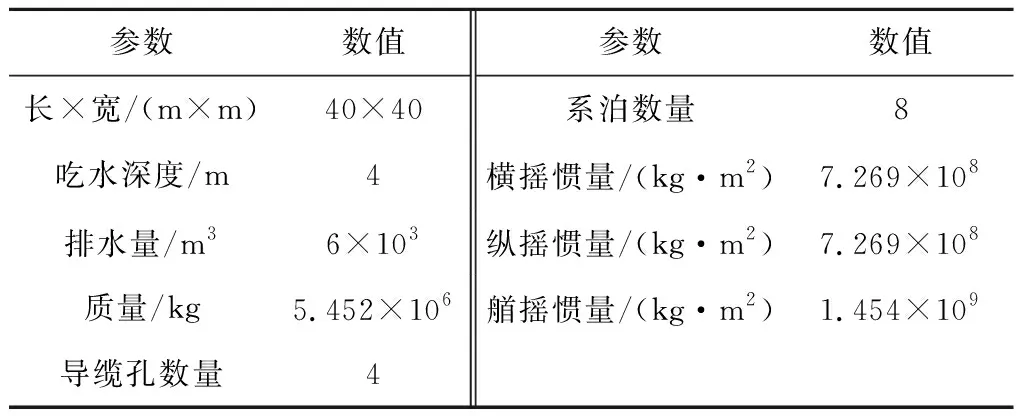
表2 ITI Energy Barge平臺參數

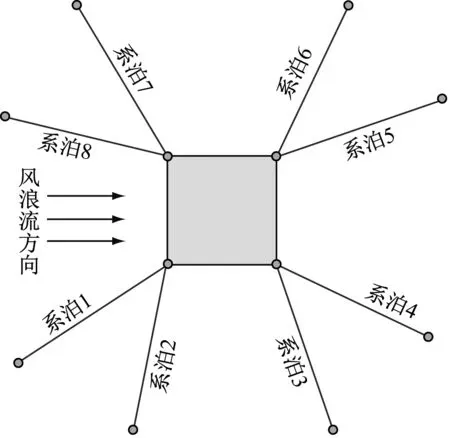
圖2 系泊示意圖

表3 系泊參數

2 載荷與環境參數

現役漂浮式風力機在極端海洋環境中會受到風、浪及海流等多種載荷作用，其葉片受到的風載荷和漂浮式平臺受到的波浪及海流載荷最為顯著[17]。

2.1 風載荷

風力機上部葉片受到的載荷主要為風載荷，筆者基于葉素動量理論，采用動態入流理論(Dynamic Inflow Theory，DIT)求解葉片平面的誘導速度，計算沿葉片展向各位置的攻角大小[18]。其誘導速度為：

(1)

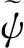
葉片受到的推力dQ和扭矩dN如式(2)所示：

(2)

式中：ρ為空氣密度；Ω為葉片轉速；b為切向誘導因子；c為距輪轂中心r處風力機葉片弦長；θ為來流攻角；Cl為升力系數；Cd為阻力系數；a為軸向誘導因子；U∞為來流速度。

2.2 波浪載荷

因Barge平臺體積較大，其對波浪場的影響難以忽略，需考慮平臺在水中的繞射效應，為此筆者基于輻射/繞射理論求解平臺在水中的波浪載荷。其中速度勢函數φ如式(3)所示[19]：

(3)

式中：φi為入射勢；φd為繞射勢；φr為輻射勢;j為平臺自由度個數。

上述函數需滿足拉普拉斯方程及邊界條件：

(4)

式中：g為重力加速度；η為入射波波面函數；t為延遲時間;n為浮體濕表面外法向量。

故Barge平臺承受的波浪力FW和波浪力矩MW可記為：

FW=?SB-pmdSB

(5)

MW=?SB-p(r×m)dSB

(6)

式中：SB為浮體濕表面面積；p為壓強；r為結構物表面到基點矢量；m為結構物表面法線方向。

2.3 海流載荷

因海流速度較為緩慢，其對海工結構的作用力主要體現為拖曳力Fc，可記為[20]：

(7)

式中：ρs為海水密度；Cd為阻力系數；A為平臺沿海流方向的等效面積；Uo為流速。

2.4 環境參數

假設海流為均勻流，流速為0.8 m/s。依據IEC 61400-3海上風力機設計要求，基于Jonkman等[21]所提出的方法，采用Kaimal風譜，生成11.4 m/s的湍流風場，結果如圖3所示。

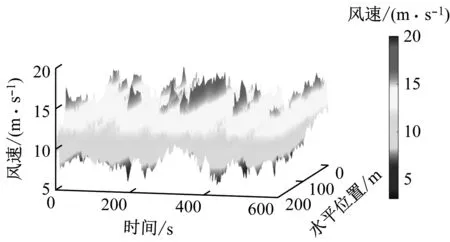
圖3 湍流風速譜

采用P-M譜生成波浪，譜峰周期為10.1 s，有義波高為6 m，不規則波高時歷曲線如圖4所示。

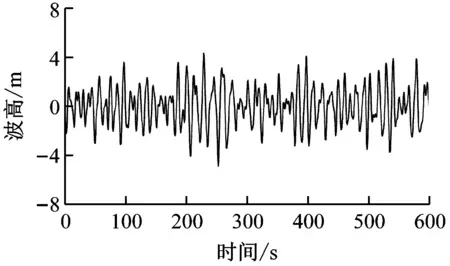
圖4 波高時間序列

3 深度學習

3.1 CNN原理

CNN作為典型的前饋神經網絡，是一種端到端的數據處理方法，具有強大的特征提取能力，其本質是構造多個濾波器,逐層提取隱藏在原始數據中的特征信息，具有局部接受域、參數權值共享及稀疏式連接等特點，可有效避免數據冗雜與過擬合問題[22]。傳統CNN模型主要包括卷積層、激活函數、池化層和全連接層。

3.1.1 卷積層

卷積運算作為CNN的核心，其通過矩形卷積核提取原數據，結合參數共享機制，將原始數據與卷積核進行卷積計算，輸出特征數據[22]。其表達式為：

xi+1=Wi⊙xi+bi

(8)

式中：xi+1為卷積后的數據；xi為卷積前的數據；⊙為卷積運算符；Wi為權重矩陣；bi為偏置項。

3.1.2 激活函數

為對卷積后的數據進行非線性變換，采用激活函數進行預處理。常用的有Tanh、Sigmoid及Relu激活函數[23]，筆者選用Relu函數，既避免了Sigmoid函數梯度消失問題，又提高了計算效率[22]。式(8)經變換得：

yi=f(xi+1)=f(Wi?xi+bi)

(9)

式中：yi為變換后的數據；f(·)為Relu激活函數。

3.1.3 池化層

為解決卷積層特征提取后數據量及維度增加造成的維數災難問題,在保證原特征信息不丟失的基礎上，基于池化對前特征數據進行約簡。筆者采用最大值池化,從池化核所對應的區域中選出最大值作為代表值，可反映原數據最顯著的特征，其表達式為：

max-pooling(f[i-1],f[i],f[i+1])=

max(f[i-1],f[i],f[i+1])

(10)

式中：max-pooling為最大池化函數；f[i]為第i個像素值；max(·)為取最大值函數。

3.1.4 全連接層

全連接層為卷積池化與分類器的連接過渡部分，通過與卷積池化層的所有神經元連接，整合具有區分性的特征信息。經卷積池化后的特征信息輸入全連接層,轉化為一維特征向量，最后采用Softmax分類器進行分類[23]。

3.1.5 學習技巧

為防止CNN網絡過擬合與提高診斷準確率，常采用一些學習技巧提高CNN性能。經長期實踐總結，批量歸一化(Batch Normalization, BN)、數據增強及Dropout技術等被廣泛應用，筆者采用BN及Dropout技術處理原數據。其中，BN技術是指將原數據處理為同數量級的規范數據，防止梯度消失與梯度爆炸問題。Dropout技術會隨機舍棄網絡模型中一定比例的神經元，讓極少部分異常數據進入模型學習，以減少其對模型的影響[24]。

3.2 CNN模型構架

針對本文所分析的系泊蠕變動態響應，設計如圖5所示的CNN模型框架。模型參數見表4。

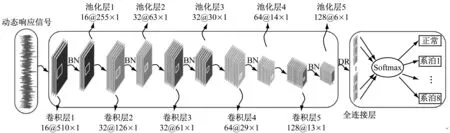
圖5 CNN模型

4 混沌理論

分形理論作為現代非線性科學研究中十分重要的分支,表現為系統部分與整體之間存在自相似性,可定量描述非線性系統的分形特征。混沌作為時間尺度上的分形,具有敏感性、分維性、隨機性及普適性等特點,可用于分析非線性動力學系統的不穩定發散過程[14]。

4.1 相空間重構

相空間重構是由Packard等[25]提出的一種通過重構吸引子軌跡還原系統非線性特征的方法。分析動態響應信號動力學特征時，將一維時間序列{yi|i=1,2,…,M}嵌入d維空間中得到相點X：

(11)

式中：N為第N個樣本；d為嵌入維數，d≥2r′+1；r′為系統自變量個數。

嵌入維數d和延遲時間t對結果影響顯著。d過小，吸引子無法充分展開，出現混疊現象；d過大，計算效率降低并引入噪聲，難以體現動力學特性。t過小，各坐標缺乏獨立性；t過大，不同時間下各坐標復雜度增加。

考慮到Cao方法[26]適用樣本量少的信號和互信息函數法[27]可反映數據間的相關性，筆者基于Cao方法與互信息函數法計算嵌入維數d和延遲時間t，并將其作為構建混沌相圖參數組合。

4.2 最大Lyapunov指數

混沌理論可體現動態系統中各成分間非線性相互作用，發現隨機現象中的真實規律。為定量表示系統混沌特性，基于最大Lyapunov指數L[1]反映非線性響應信號特征信息，當L>0時，系統具有混沌特征，且與L呈正相關，反之系統無混沌特征。采用Wolf法[28]計算最大Lyapunov指數，其表達式為：

(12)

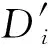
4.3 診斷流程

采用深度學習與混沌理論對各系泊蠕變階段的平臺艏搖響應數據進行分析，重點研究系泊是否發生蠕變及蠕變系泊位置。具體流程如圖6所示。

圖6 系泊診斷流程圖

5 結果與分析

5.1 系泊蠕變下漂浮式風力機動態響應

漂浮式風力機安全穩定運行需系泊為其提供回復力，當系泊發生蠕變失效后，其長度和剛度發生小幅變化，該系泊為平臺所提供的回復力發生改變，進而影響平臺的動態響應。

考慮風、浪、流同向入射時平臺響應最為強烈，系泊承受載荷最大，拉力波動最劇烈，其失效的可能更大[29]，故設置風、浪、流均垂直于風力機平面入射。

因Barge平臺8根系泊對稱分布，對其中4根發生故障時的平臺動態響應進行研究。風波作用下，分析系泊正常、蠕變與失效下六自由度上動態響應與1號、2號、3號和4號系泊在各階段的最大響應幅值，結果見圖7。

圖7中，0～3 000 s、>3 000～6 000 s與>6 000～9 000 s分別為系泊正常、蠕變及失效時的漂浮式風力機平臺動態響應。其中，柱狀圖分別代表不同系泊在3個階段的最大響應幅值，分析各系泊在蠕變與失效階段的動態響應可知:(1)垂蕩及縱搖動態響應變化較小；因系泊狀態改變導致受力不均，平臺受到的扭矩發生變化，橫搖和艏搖響應急劇增大；平臺縱向與橫向受力不均造成縱蕩與橫蕩響應增大。(2)系泊失效后，平臺響應幅值急劇增大，但在蠕變階段，風力機平臺在各自由度的動態響應變化極小。(3)不同位置的系泊狀態變化對平臺穩定性影響不同，遠離迎風浪側的3號、4號系泊影響較小，靠近迎風浪側的1號、2號系泊影響較大。

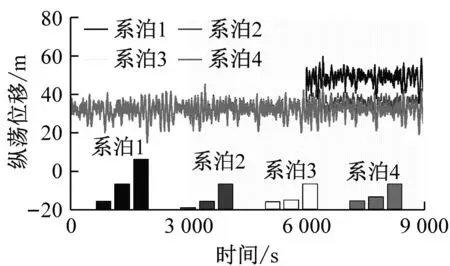
(a) 縱蕩

考慮系泊失效后平臺動態響應急劇增大，風力機安全運行受到極大威脅。但在系泊蠕變階段動態響應變化極小，不易發現，故在系泊蠕變階段發現問題，對風力機平臺動態響應數據進行分析和診斷，對提前預防系泊失效與保證風力機安全運行具有重要意義。

當系泊狀態發生改變時，平臺艏搖較其他自由度動態響應更為敏感，故對各系泊蠕變階段的平臺艏搖響應數據進行分析，其時域響應如圖8所示。

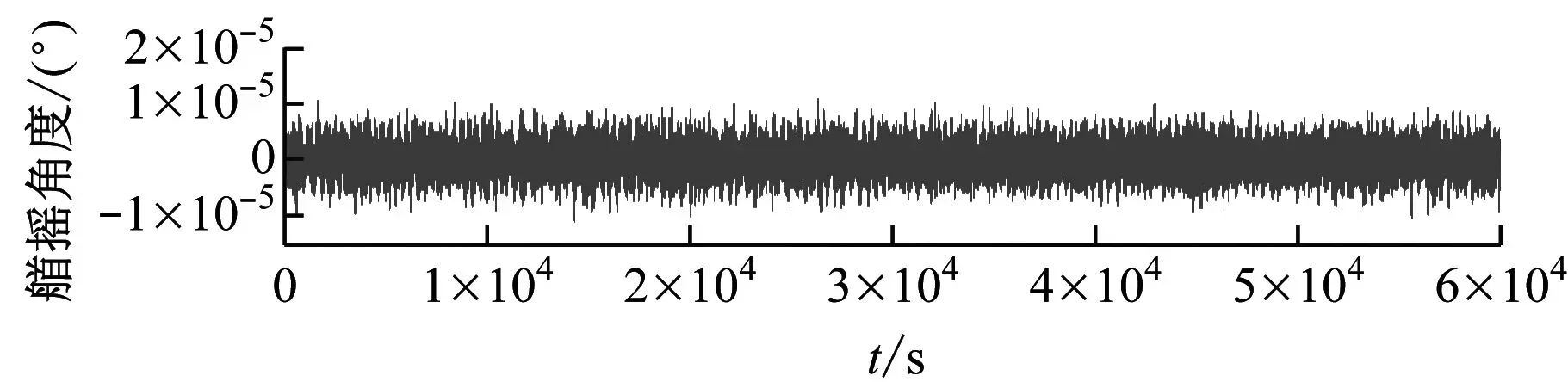
(a) 正常系泊

由圖8可知，正常系泊與故障系泊時域圖存在顯著差異，可判斷系泊是否發生蠕變，但無法準確識別蠕變系泊位置。為提取有效故障特征，基于相空間重構法繪制系泊蠕變三維吸引子軌跡，分析各系泊動力學系統混沌特性，采用Cao方法[26]與互信息函數法[27]計算最佳延遲時間t和嵌入維數d，結果見表5。

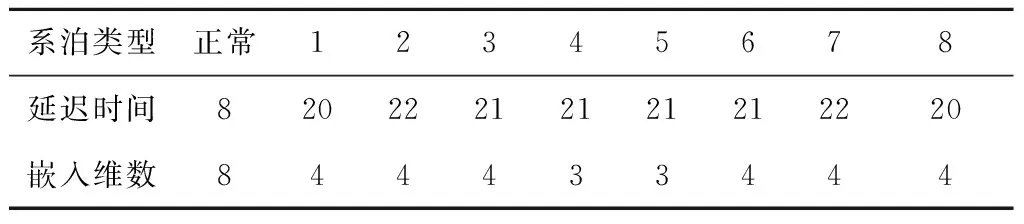
表5 最佳延遲時間與嵌入維數

各系泊狀態吸引子軌跡如圖9所示。分析圖9可知，正常系泊與故障系泊相圖存在顯著差別，形態各異，但均呈冗雜毛球狀，表現為非完全隨機也非完全周期響應，表明各系泊動態響應信號具有顯著的混沌特性。為定量表示，計算各系泊信號的Lyapunov指數，結果見表6。由表6可知，各系泊平臺艏搖響應信號的Lyapunov指數均大于0，表明具有不同程度的混沌特性。

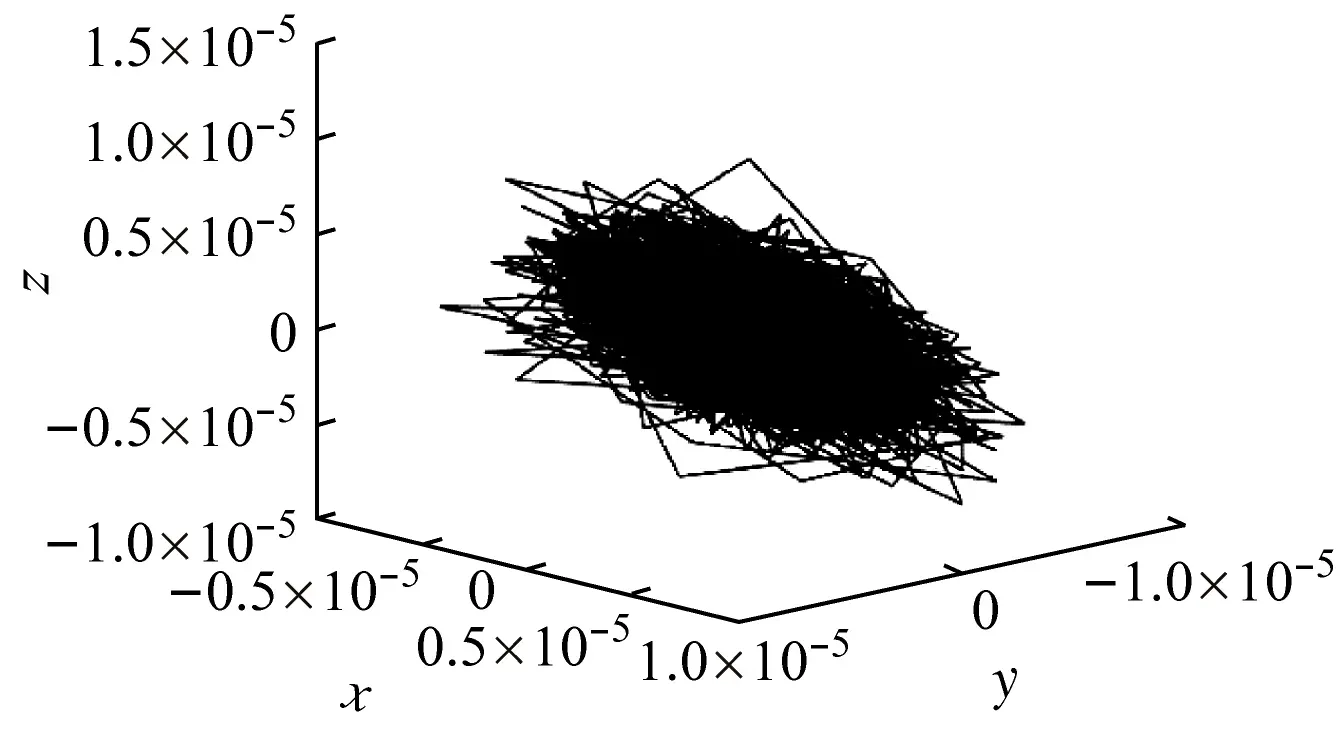
(a) 正常

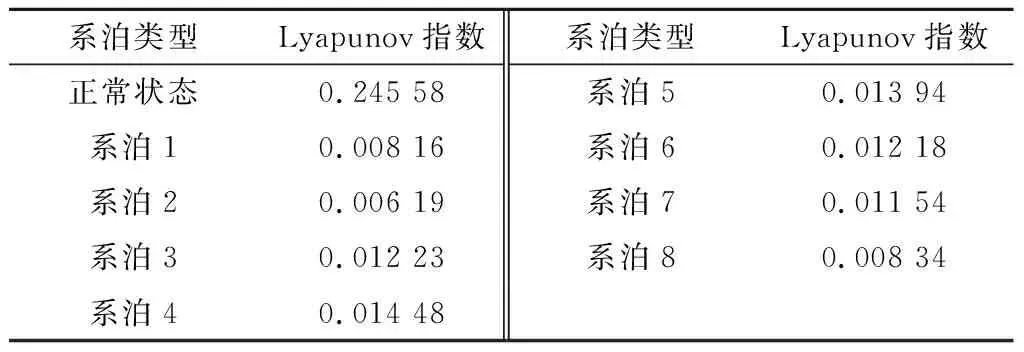
表6 各系泊信號Lyapunov指數

5.2 CNN模型學習

為提取混沌序列中非線性特征信號并進行故障分類，將平臺艏搖響應信號按8∶1∶1的比例分為訓練集、驗證集和測試集，輸入CNN模型中訓練，設置迭代140輪，每輪100次。蠕變系泊位置分類準確率及損失曲線如圖10所示。由圖10可知，CNN方法可較好地進行狀態識別，迭代達到22輪時準確率與損失率均幾乎不再改變，此時準確率高達98.86%，損失率為0.051 7，模型未發生過擬合現象，表明該方法可提取出純凈動態響應信號。

(a) 準確率

為更清晰地展示模型對蠕變系泊位置的分類效果，引入混淆矩陣進行識別，結果如圖11所示。其中，橫軸為預測類別，縱軸為實際類別，主對角線表示正確分類樣本數。由圖11可知，僅系泊4蠕變被誤判為系泊5蠕變，其余蠕變系泊位置分類均無錯誤，總體分類準確率較高。

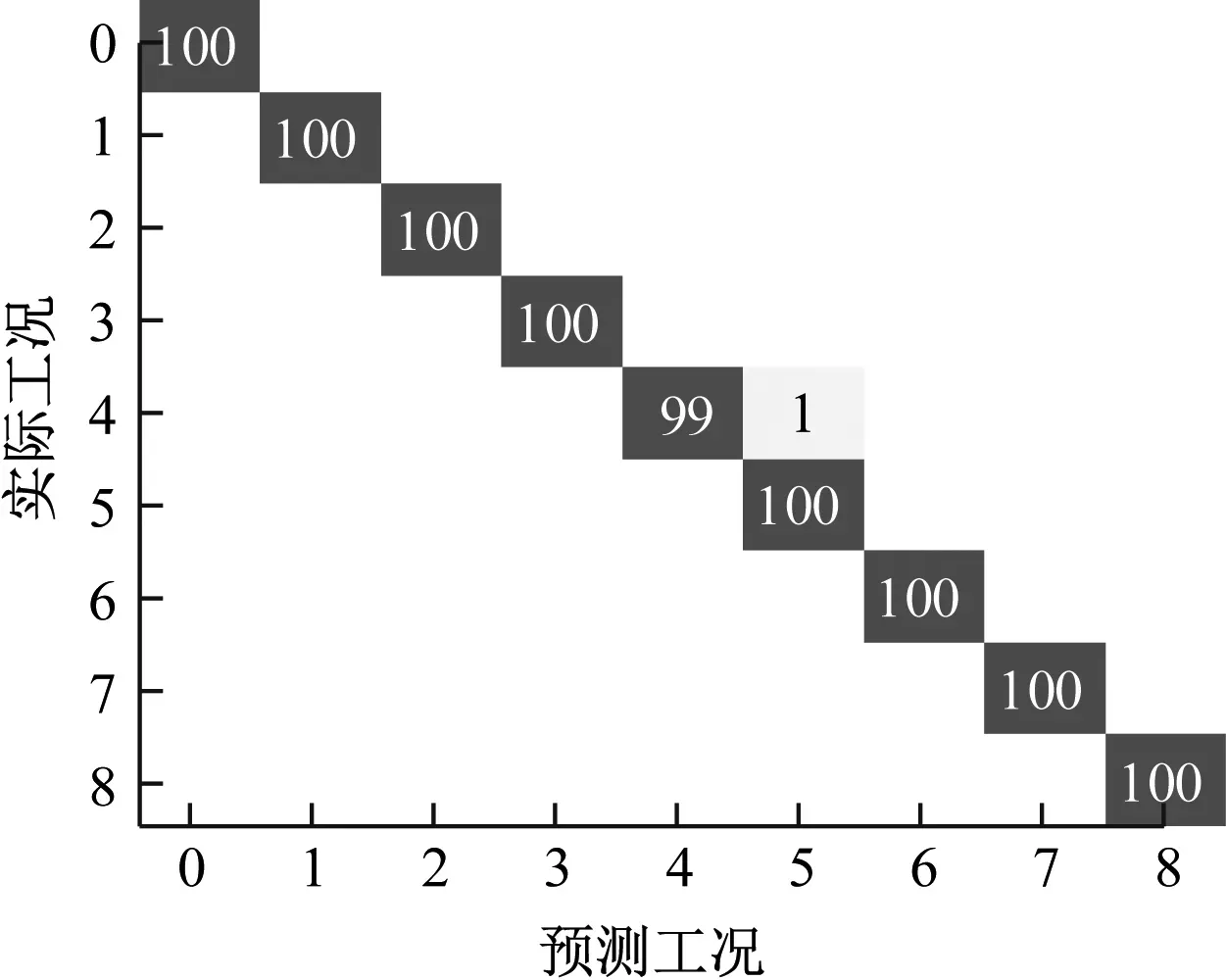
圖11 故障診斷多分類混淆矩陣

5.3 模型可視化

為證明本文所提方法的特征提取及分類能力，采用t-SNE[30]對提取的特征信號進行降維，可視化故障特征，結果如圖12所示。由圖12可知，隨卷積層數增加，對數據特征捕捉逐漸深入，各蠕變系泊類間距增大，在卷積層2中已出現點簇分離現象，其中正常系泊已明顯分離；在全連接層中，各蠕變系泊已可明顯區分，表明CNN可從混沌序列中提取純凈非線性信息。

為進一步了解卷積層學習特征屬性，可視化卷積層1與卷積層5所提取的特征信號，分析其混沌特性，圖13和圖14給出了吸引子軌跡。由圖13和圖14可知，各蠕變系泊吸引子軌跡具有顯著混沌特征，隨著卷積層數增加，吸引子由混沌無序朝有序性發展。為定量表示其混沌特性減弱、純凈性增強，計算各蠕變系泊原始數據與卷積層5的Lyapunov指數L，結果如圖15所示。考慮L>0時，系統具有混沌特征，且其非線性隨L增大而增強[28]。由圖15可知，各狀態系泊原始數據經相空間重構后計算得到的L大于在CNN模型卷積層5所提取數據計算得出的L，表明平臺艏搖動態響應經CNN模型卷積池化等操作后非線性降低，即本文所提出的方法可提取較為純凈的非線性信息。

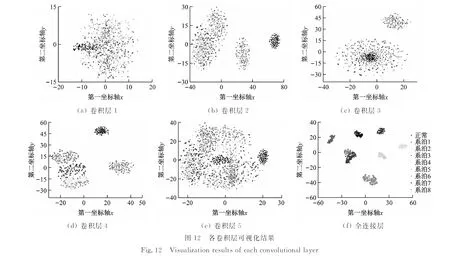
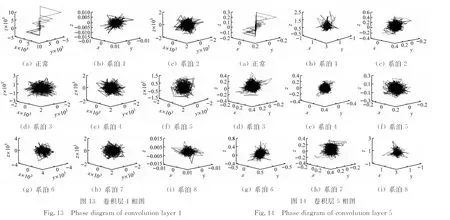
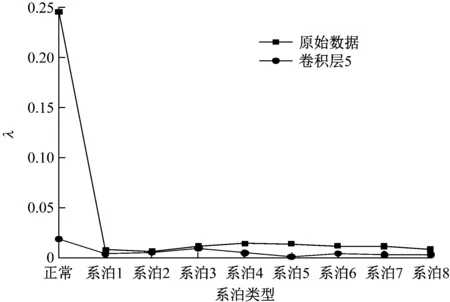
圖15 原始數據與卷積層5的Lyapunov指數

6 結 論

(1) 系泊蠕變階段，平臺響應變化極小，但系泊失效后平臺響應急劇增大，其中艏搖響應更為敏感。

(2) 經CNN處理后的系泊平臺響應分類準確率高、損失率低，且收斂速度快。

(3) 采用t-SNE降維后，不同系泊蠕變的平臺艏搖響應信號可明顯區分。

(4) 結合吸引子軌跡與Lyapunov指數可反映信號混沌特性，其中Lyapunov能夠定量表示CNN可從混沌序列中提取純凈非線性信息。