基于深度強化學習的移動機械臂末端滑模控制技術

朱引行

（江蘇省漣水中等專業學校,江蘇 漣水223400）

引言

近年來，隨著機器視覺技術的不斷創新與發展，相關領域的研究也得到了進一步深入，最具代表性的便是移動機械臂的控制與應用。在智能化與伺服控制技術的輔助下，移動機械臂的應用范圍逐漸擴大，應用效果明顯提高。但是，由于人們對于自動化標準的提升，傳統的控制技術已經無法滿足需求和標準，部分移動機械臂在高強度的工作環境下，末端的滑模逐漸顯現出一定的問題與缺陷，對于日常的工作會形成不定性的消極影響。移動機械臂的末端滑模是一項十分關鍵且重要的控制元件[1]，應用中起到“承上啟下”的作用，不僅能夠加強機械臂對于指令的接收速度，同時，進一步拓展了機械臂的移動空間，逐步營造穩定的工作環境[2]。但是過度移動導致滑模出現裂縫、破損等問題，對于日常的移動、振動控制會形成一定的阻礙[3]。因此，本次結合深度強化學習原理，設計優化移動機械臂末端滑模控制技術，以此為進一步完善整體的應用效果。考慮到最終測試結果的可靠性，選擇較為真實的目標作為測試的對象，根據移動機械臂的應用需求、標準，對滑模的控制形式以及范圍作出對應的調整。當處于復雜環境下時，滑模的控制壓力也會得到緩解，從整體上降低對機械臂的阻礙，更加快速、穩定地完成伺服任務，同時也具有自主定位和跟蹤的能力，具有關鍵的現實應用意義。

1 設計移動機械臂末端滑模單元控制技術

1.1 自適應預處理

在對深度強化學習下移動機械臂末端滑模控制技術進行優化設計之前，需要先結合移動機械臂的作用區域，進行自適應預處理[4]。所謂自適應預處理，主要是針對于機械臂滑模的控制環境，設定的一種動態的控制協議。結合深度強化學習原理，增設辨識機制、非線性動力模型以及異常定位裝置，加強對移動機械臂末端滑模的自適應控制程度[5]。利用關聯設備，先獲取部分基礎控制數據，完成匯總整合之后，為確保自適應控制環境的穩定，需要先計算出滑模預設移位率，具體如公式（1）所示：

式中：H 表示滑模預設移位率，φ 表示收斂系數，i 表示定向辨識時限，表示自適應滑動比，c1便是預設移位距離，c2表示實測移位距離。通過上述計算，最終可以得出實際的滑模預設移位率。將其預設為滑模的移位標準，同時，關聯機械臂內部的非線性控制系統，結構中需要安裝自適應感知設備，同時，增加提高軸孔裝配、目標捕獲等裝置，從整體上增加機械臂的自適應控制速度與安全程度，確保自適應控制系統的穩定性，完成自適應處理，為后續的控制處理奠定基礎條件。

1.2 布設多模態感知滑模控制節點

結合實際的控制標準，布設一定數量的多模態感知控制節點。提取機械臂滑模的移動特征，加工控制系統與核心感知節點相關聯，但需要注意的是，整個過程必須要結合機械臂視覺伺服的控制律。為避免感知失敗問題的出現，需要在特定的環境之中，設定一個限制控制區域，導入控制特征，具體的原理，見圖1。

圖1 多模態感知原理圖

根據圖1，可以完成對多模態感知原理的設計與調整，針對于移動機械臂的應用范圍，調整末端滑模的偏移方向，同時需要設定兩側的偏移指標數值。完成基礎調整之后，可以先測定此時節點收集的末端滑模控制數據是否發生較大變化，如果與基礎數值對比，出現的差值較大，則需要重新設定個偏移指標，確保控制程序的穩定執行，一定程度上也有利于多模態感知控制節點對機械臂末端滑模的控制。

1.3 多協調控制軌跡設計

在完成對多模態感知控制節點的布設之后，接下來，需要設計多協調控制軌跡。通常情況下，多指令機械臂日常工作效率要比單指令機械臂更高，主要是由于其內部的程序可以同時針對多個目標處理，實現多維度的同步控制，還可以適應較多的應用場景，以此應用效果更佳。可以采用控制指令來代替傳統的數字化軌跡控制目標，形成穩定的指令集群，構建多協調的控制程序，將多個目標控制軌跡作為約束條件，增設在不同的主從控制和約束環境之中，結合混合控制算法，計算出機械臂間的同步誤差，具體如下所示：

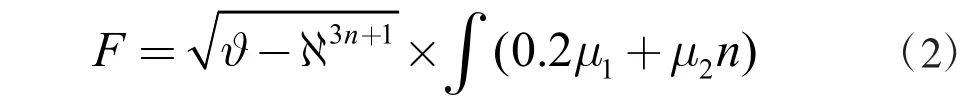
式中：F 表示機械臂間的同步誤差，? 表示同步響應時間，? 表示協調范圍，μ1表示約束軌跡距離，μ2表示無向圖放松約束軌跡距離，n 表示控制次數。通過上述計算，最終可以得出機械臂間的實際同步誤差。在標定的誤差范圍之內，可以合理調整移動機械臂的覆蓋區域和控制范圍，結合預設的控制約束條件，實現軌跡的定向同步。但是需要注意的是，針對于移動機械臂的控制軌跡，通過多協調的模式，營造拓撲軌跡測定約束框架，并形成一種定向的阻抗，加強末端滑模的移動速度，與末端的執行器響應接觸，提升工作精度，降低控制誤差。

1.4 構建深度強化學習末端滑模控制模型

在完成對多協調控制軌跡的設計之后，接下來，需要結合深度強化學習原理，構建末端滑模控制模型。首先，需要先將機械臂中的軸孔與軸入孔接觸，形成對應的操作空間，控制處理過程中，沖擊碰撞是難以避免的，為降低對末端滑模的影響以及損壞，可以引入Hogen 提出阻抗機制，在交互環境之中，結合所獲取的數據信息，計算出此時滑模的阻尼系數。隨著機械臂的移動與應用，測定分析滑模阻尼系數的變化狀態，調整滑模控制模型的指標數值，具體見表1。

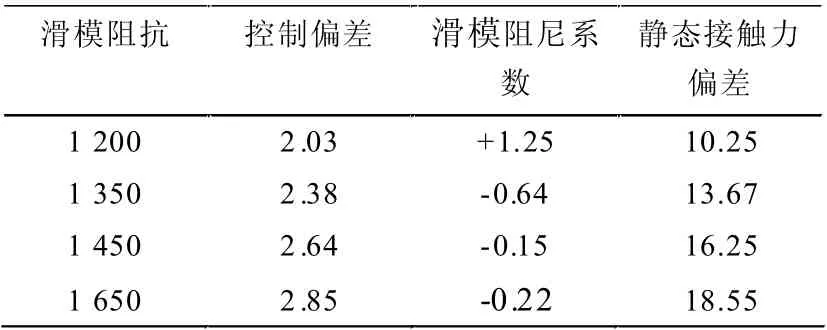
表1 滑模控制模型指標數值設定表

根據表1，可以完成對滑模控制模型指標數值的設定。隨后，根據調整的狀態，防止工件損壞，將滑模與接觸設備形成一種定向的動態聯系，設計末端滑模的阻抗控制結構。擴大實際的控制范圍，并對標定的控制程序和結構作出調整。通過改變慣性、阻尼系數以及剛度參數來調整動態控制聯系，實現多維度的深度強化學習處理。此時，采用深度強化技術，計算出標定的控制修正量，具體如下所示：

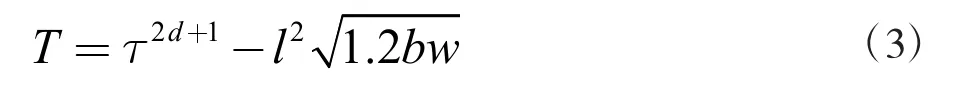
式中：T 表示控制修正量，τ 表示滑模深度強化距離，d表示單向移位時間，b 表示目標位置，w 表示測定位移，l 表示深度接觸力。通過上述計算，最終可以得出實際的控制修正量，設定模型的控制范圍，并與設定的控制節點相互關聯。

1.5 PD 雙向控制矩陣設計

結合PD 控制技術，根據末端滑模的控制需求、標準，設計對應的雙向控制矩陣。首先，利用控制模型，先獲取移動機械臂的實時數據及信息，并在標定的轉換范圍之內，測定出機械臂在移動過程中的穩態誤差，具體見表2。

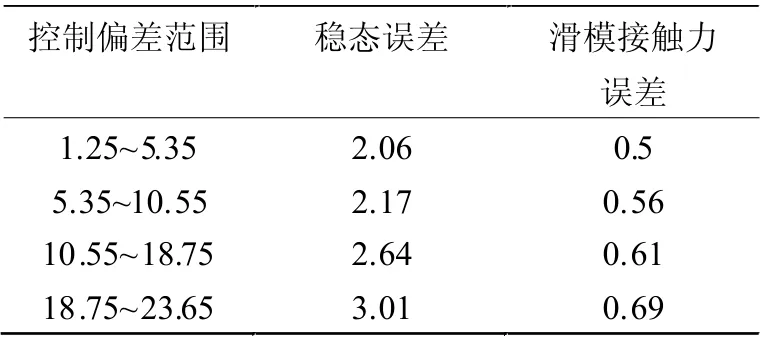
表2 機械臂移動穩態誤差測定表

根據表2，可以完成對機械臂移動穩態誤差的測定與分析。由于滑模在不同的環境下出現的偏差不同，因此，針對于滑模變動的剛度系數，測定出機械臂滑模的實際力位控制效果。但是需要注意的是，為了保證控制程序的穩態，好需要加強對滑模接觸狀態的控制，此時可以結合上述測定出的數值，設計PD 雙向控制矩陣，設定穩態誤差等于0 時，滑模的剛度系數為1.25 以下，控制程序的接觸力誤差為5.25；而當穩態誤差小于或者大于0 時，滑模的剛度系數為1.25 以上，控制程序的接觸力誤差為10.45～20.35 之間，此時末端滑模的控制軌跡為呈現出側向的曲線，利用阻抗模型關聯二階控制平臺，設定雙向控制環節，結合深強化學習技術，結合動態響應模式，構建矩陣的對應控制原理，具體見圖2。

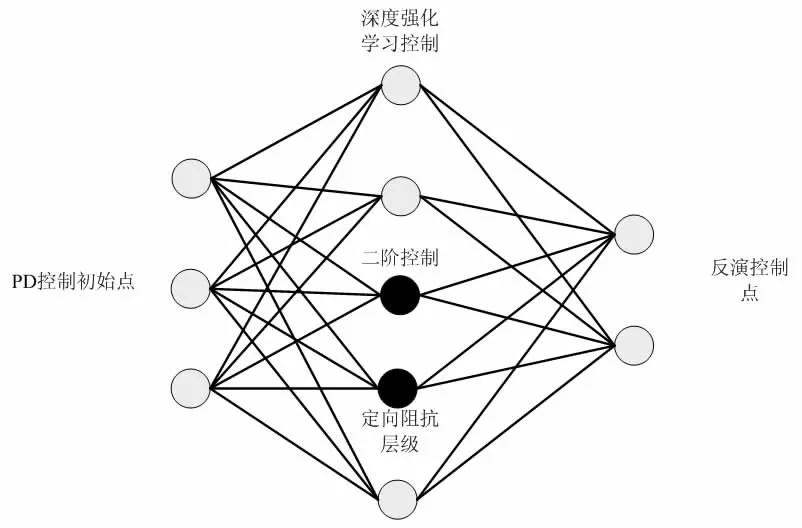
圖2 深度強化學習下PD 雙向控制矩陣原理圖示

根據圖2，可以完成對深度強化學習下PD 雙向控制矩陣原理的設計，結合上述環節，劃定末端滑模具體的控制矩陣，同時結合強化學習技術，建立ke 與xe 的誤差控制極限點，盡量控制減少穩態誤差，并在合理的范圍之內，對滑模的移位情況作出調節，增強末端控制的動態與靜態控制效果。

2 方法測試

2.1 測試準備

選擇G 企業的機械臂作為測試的主要目標對象，并設定傳統伺服定位控制技術（方法1）測試組、傳統改進分數控制技術（方法2）測試組以及本文所設計的深度強化學習控制技術測試組。結合自抗擾控制與深度強化學習技術，構建改進ESO 的滑模控制程序，并設定機械臂末端滑模的基礎指標參數：單元抖振次數5 次，有效控制距離15.35 m，末端變動誤差2.03。

2.2 測試過程及結果分析

在標定的測試環境之中，設定三個擾動節點，布設在機械臂的控制節點之中，在控制程序之中，設計滑模面的動態控制環節，確保達測定標準即可。設定標準的抖振比為1∶3.5，測定機械臂在移動的過程中控制系統的魯棒性，并測算末端滑模的轉動慣量，一般需要控制在1.75～6.45 之間，確保滑模可以順利移動，降低整體的移位偏差概率。結合深度強化學習技術，在周期之內，定位滑模的移動位置，并對其出現的穩態誤差進行分析，具體見圖3。

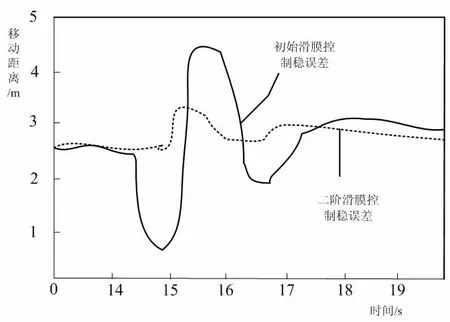
圖3 末端滑模穩態誤差局部變化圖示

根據圖3，可以完成對末端滑模穩態誤差局部變化的分析與研究。經過觀測可以的差值，經過控制調整和處理，末端滑模的穩態誤差得到了明顯的控制，逐漸趨于平穩，這表明誤差逐漸減少。此時，啟動設定的三個擾動節點，設定處理目標，確保在相同的環境之下，計算出單元控制時間，具體如下所示：

式中：R 表示單元控制時間，η1表示預設擾動范圍，η2表示實測擾動范圍，? 表示實時轉動慣量差值，V 表示等效控制距離。通過上述計算，最終可以得出實際的單元控制時間。結合上述的測試結果，采用對比的形式展開分析，具體見表3。

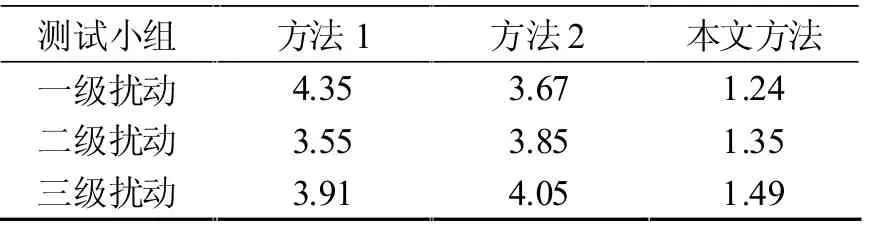
表3 單元控制時間測試結果對比分析表（s）

根據表3，本研究方法將單元控制時間均控制在了1.5 s 以下，控制的速度與效率表現較好，具有實際的應用價值。

3 結論

結合深度強化學習設計移動機械臂末端滑模控制技術。利用深度強化學習原理，逐步構建統一的滑模控制標準，從根源上降低整體的控制誤差，增強度滑模控制的反向作用能力，再加上異常定位技術與末端監測技術的輔助，可以營造更加細化的控制模式，為后續的技術創新奠定參考依據。