基于改進鯨魚算法和神經網絡的食品機器人能耗軌跡規劃

黃崇富 常 宇 劉力超

(1. 重慶工程職業技術學院，重慶 402260；2. 中煤科工集團重慶研究院有限公司，重慶 400037；3. 四川大學錦城學院，四川 成都 611731)

隨著工業機器人技術的快速發展，食品機器人逐漸被應用于食品原材料搬運、碼垛、揀取等領域[1-2]，對食品生產效率產生了深遠的影響[3-4]。食品機器人軌跡規劃的目的是通過合理支配末端執行器以及各個關節的位移、速度等參數，降低能耗、減少機械磨損、保證運動平穩和提高機器人性能[5]。

食品機器人運動軌跡規劃可劃分為末端執行器軌跡規劃和關節空間軌跡規劃2種類型[6]，末端執行器軌跡規劃需重復求解逆運動方程，計算量大；關節空間軌跡規劃將關節變量表示為時間函數，只需少量逆運動學計算，更適用于食品機器人點到點運動軌跡規劃問題[7]。普亞松等[8]提出了一種混合多項式插值的關節軌跡規劃方法，得到的規劃角速度波動更小，運行更平穩，但該算法需人為設定中間目標點角速度等參數；田國富等[9]采用內插法替代多項式插值，實現了對關節的連續運動軌跡規劃，但存在角速度峰值較大的缺陷。在食品加工環境中，機器人動力學參數往往是未知的，這就需要進行機器人動力學辨識[10-11]，然而，采用最小二乘法[12]、工具變量法[13]等傳統動力學參數估計方法，得到的動力學參數模型形式單一，只適用于特定場景。趙俊宇等[14]提出了一種基于平行BP網絡的動力學辨識模型，并采用LM算法對模型進行訓練，仿真結果驗證了該模型能夠有效擬合關節力矩，但該算法在訓練階段耗時較多，且模型參數探索容易陷入局部最優。

研究擬對食品工業機器人動力學參數未知情況下的節能軌跡規劃問題進行分析，提出一種基于鯨魚算法和神經網絡的點到點機器人關節能耗軌跡規劃方案，設計基于神經網絡的相似動力學辨識，采用改進的鯨魚優化算法(Whale Optimization Algorithm，WOA)[15]對動力學辨識模型參數進行優化；在此基礎上，利用四次多項式插值對關節軌跡進行規劃，將軌跡參數等效為WOA編碼，通過優化求解關節能耗目標函數，從而得到能耗最優的關節運動規劃軌跡，旨在有效實現動力學參數未知下的軌跡規劃，使軌跡能耗更低。

1 食品機器人節能軌跡規劃問題描述

食品機器人點到點(PTP)的運動模式適用于食品原材料揀取、碼垛、搬運等作業場景，此時只需規定末端執行器起點和終點的姿態、位置等信息即可。對于關節數為Nr的食品機器人，其基于拉格朗日形式的動力學模型[16]為：

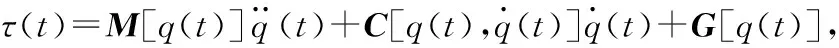
(1)

式中：

τ(t)——機器人關節力矩；

q(t)——關節角位置，rad；

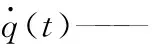
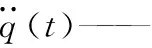
M(q)∈RNr×Nr——慣性矩陣(為對稱矩陣)；

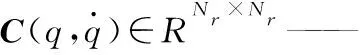
G(q)∈RNr——重力矢量。

根據文獻[16]，第i個(i∈[1,…,Nr])關節的功率pi(t)與力矩τi(t)的關系式為：

pi(t)=Ui×Di×τi(t)/Ki，

(2)

式中：

Ui——第i個關節的電壓值，V；

Di——第i個關節的傳動比系數；

Ki——第i個關節的電機轉矩常數。

由機器人關節功耗構建機器人軌跡規劃能耗目標函數f(s)：

(3)

式中：

s——給定關節路徑；

Tf——關節移動結束時間，s。

(4)

式中：

V=[v1,…,vn]T——隱含層輸出向量；

σi——第i個徑向基函數的擴展常數。

(5)

(6)

(7)

將式(5)～式(7)代入式(1)，得到關節近似動力學模型：

(8)

確定關節近似動力學模型后，采用改進的鯨魚優化算法(IWOA)對3個RBF神經網絡模型參數進行訓練。

2 改進鯨魚優化算法在食品機器人軌跡規劃中的應用

2.1 改進鯨魚優化算法的實現

鯨魚優化算法(WOA)模擬座頭鯨捕獵行為，進化過程劃分為局部搜索和全局搜索兩個階段，局部搜索采用螺旋和收縮包圍更新機制，全局搜索采用隨機搜索更新策略，有效平衡了算法探索與開發，具有較高的收斂精度和較快的收斂速度[19]。WOA存在的缺陷：① 指定全局最優解為所有個體學習進化對象，容易陷入局部最優；② 采用概率分布的方式種群初始化，影響了算法收斂速度。因此，提出改進的鯨魚優化算法(IWOA)，即采用混沌映射法對種群進行初始化，引入領域內優秀個體信息自適應更新學習進化對象。

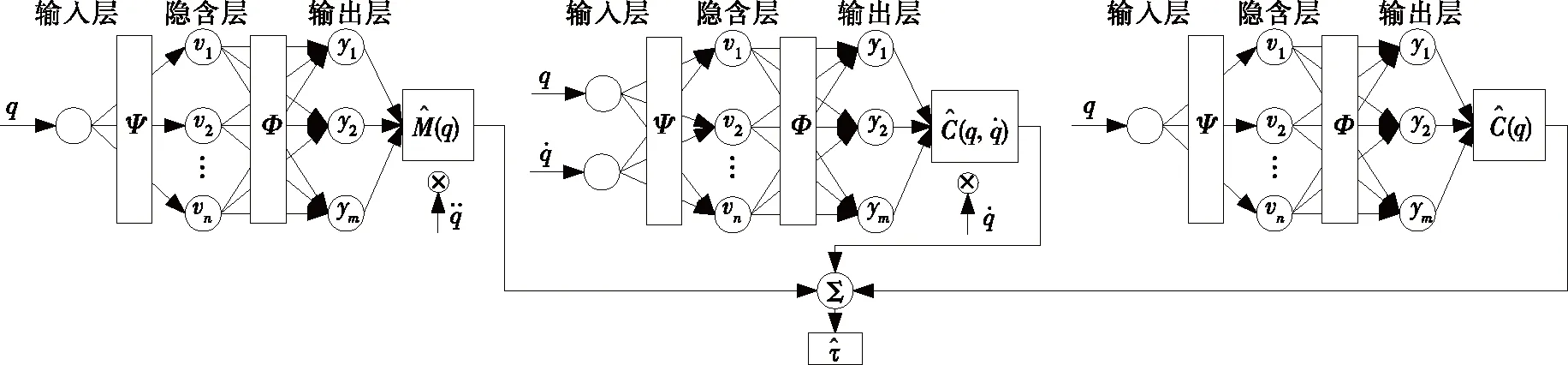
圖1 RBF神經網絡相似動力學辨識示意圖

2.1.1 混沌映射 隨機生成規模為Q的初始種群，采用Singer映射對種群內個體Xi(i∈[1,…,Q])進行混沌映射處理：

(9)

式中：

μ——混沌系數，當μ∈[0.9,1.08]時，Singer映射具有混沌行為。

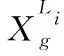
(10)

λ=1-et-Tmax，

(11)

式中：

X*(t)——WOA設定的Xi學習進化對象；

Xg(t)——當前種群目標函數值最優個體；

λ——自適應控制系數；

Tmax——最大迭代系數。

由式(10)、式(11)可知，個體Xi自適應調整向臨域內優秀個體和全局最優解學習程度，保證了種群多樣性，有助于提升算法收斂精度。選取Sphere單峰函數和Griewank多峰函數驗證IWOA收斂性能，并與基本WOA、布谷鳥算法(CA)[21]進行對比試驗，各函數收斂曲線如圖2所示。

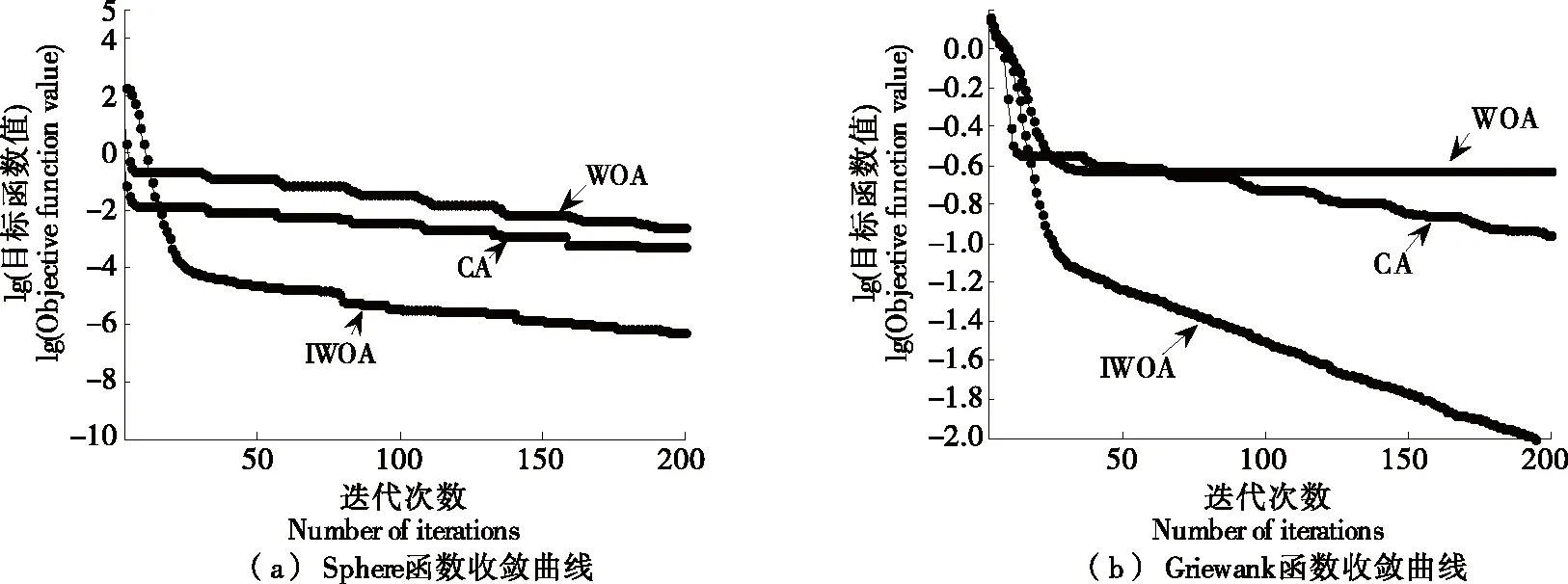
圖2 測試函數對比收斂曲線

Sphere函數用于驗證算法的收斂精度，Griewank函數用于驗證算法跳出局部極值的能力[22-23]。由圖2可知，IWOA算法全局尋優能力明顯優于CA和WOA算法，表明IWOA能夠較好地平衡局部搜索與全局搜索，收斂精度更優。

2.2 IWOA優化RBF神經網絡模型參數

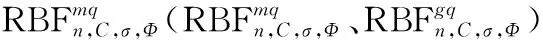
Xi=[n,c1,…,cn,σ1,…,σm,ω11,…,ω1m,…,ωn1,…,ωnm]。

(12)

將機器人關節力矩實際輸出值與網絡評估值之間的誤差平方和作為目標優化函數：

(13)

式中：

J——網絡訓練次數；

τi——第i次力矩實際輸出值。

采用IWOA優化式(13)目標函數，當算法迭代次數達到最大迭代次數Tmax或者網絡參數達到預期效果時，算法停止迭代進化，種群目標函數值最優個體對應最佳參數，代入RBF神經網絡進行學習，以實現軌跡規劃。

2.3 四次多項式關節運動軌跡規劃

利用四次多項式對食品機器人關節空間軌跡規劃過程進行描述，對于第i個關節(i∈[1,…,Nr])角度qi(t)：

qi(t)=ait4+bit3+kit2+dit+ei，

(14)

式中：

ai、bi、ki、di、ei——軌跡參數。

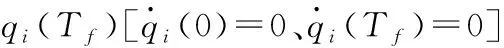
(15)

(16)

di=0，

(17)

ei=qi(0)，

(18)

將式(15)～式(18)代入式(14)得到關節軌跡描述：

(19)

(20)

(21)

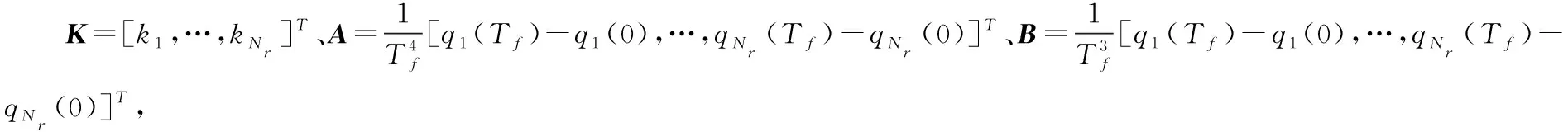
(22)

(23)

(24)

2.4 食品機器人節能軌跡規劃的實現

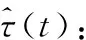
(25)

(26)

IWOA算法迭代次數達到最大值時，停止迭代進化，種群目標函數值最優個體對應最佳Kbest。根據式(15)～式(18)，利用Kbest求解A、B并代入式(14)，從而得到最優能耗軌跡規劃結果，食品機器人節能軌跡規劃實現示意圖如圖3所示。

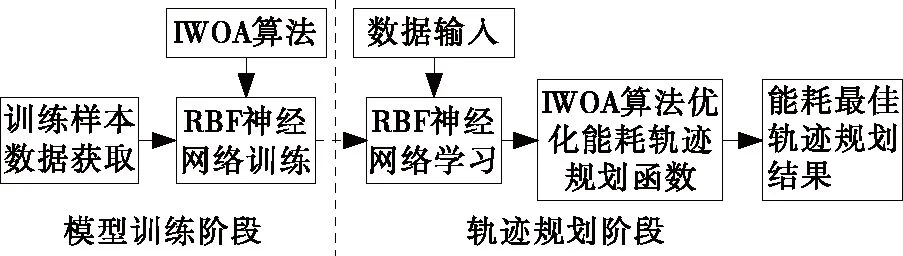
圖3 食品機器人節能軌跡規劃實現示意圖

3 仿真試驗

搭建如圖4所示的6關節食品機器人D-H坐標系(D-H參數見表1)，仿真環境為MATLAB2018a。IWOA算法參數設置：鯨魚規模Q=200，IWOA算法最大迭代次數Tmax=400，混沌系數μ=1.03，RBF網絡訓練次數J=20。

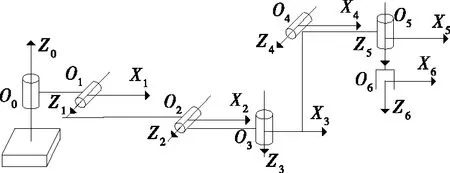
圖4 機器人D-H坐標系

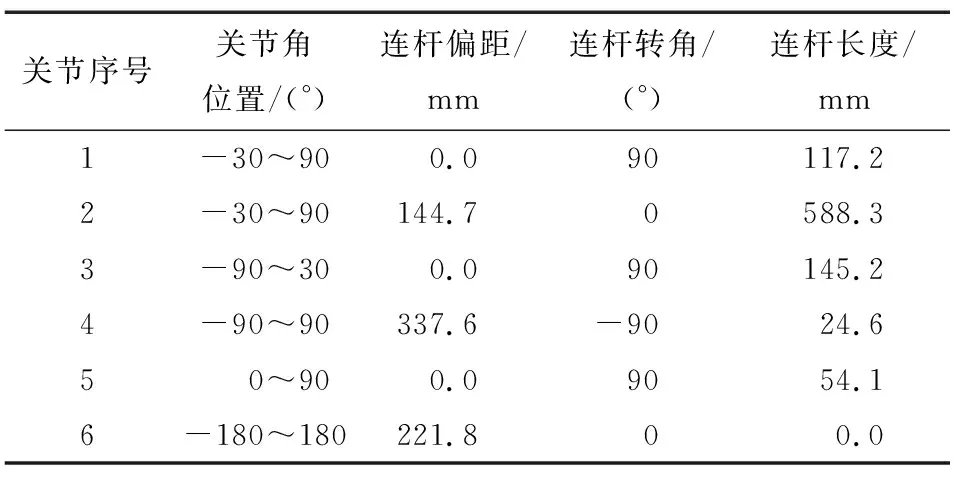
表1 D-H參數表

3.1 模型訓練

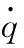
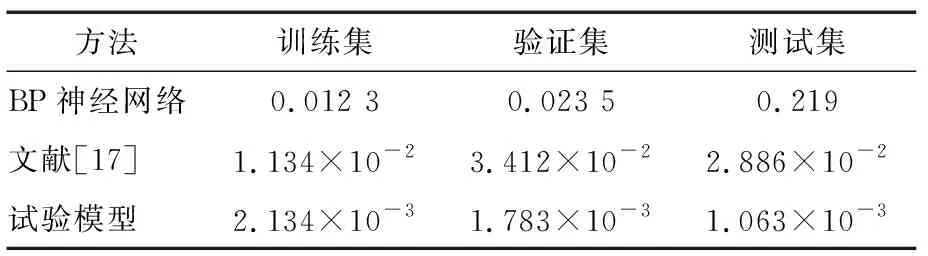
表2 模型訓練評價指標對比結果

由表2可知，無論是訓練集、驗證集還是測試集，試驗模型得到的相似動力學RMSE均優于其他兩種模型，達到了10-3N·m級別水平，表明基于試驗提出的IWOA優化RBF神經網絡的相似動力學辨識具有更好的擬合和預測能力。

3.2 軌跡規劃對比試驗

根據表1設定的機器人關節邊界條件，利用四次多項式對食品機器人關節空間軌跡進行描述，代入訓練后的RBF神經網絡，并采用IWOA對節能軌跡規劃目標優化函數進行求解，從而得到最佳食品機器人關節軌跡規劃結果。為進一步對比分析試驗所提IWOA-RBF軌跡規劃方法的性能，采取基于WOA的軌跡規劃方法WOA-RBF和文獻[6]提出的能耗軌跡規劃方法進行對比試驗，每種方法獨立運行20次。以關節5為例，不同軌跡規劃結果見圖5，不同軌跡規劃方法下關節角位置、角速度、角加速度等軌跡參數對比結果見圖6，力矩變化曲線如圖7所示，不同軌跡規劃方法指標對比結果見表3。

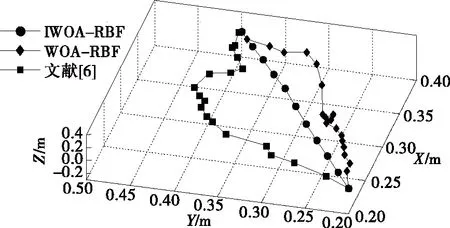
圖5 不同軌跡規劃方法軌跡規劃結果

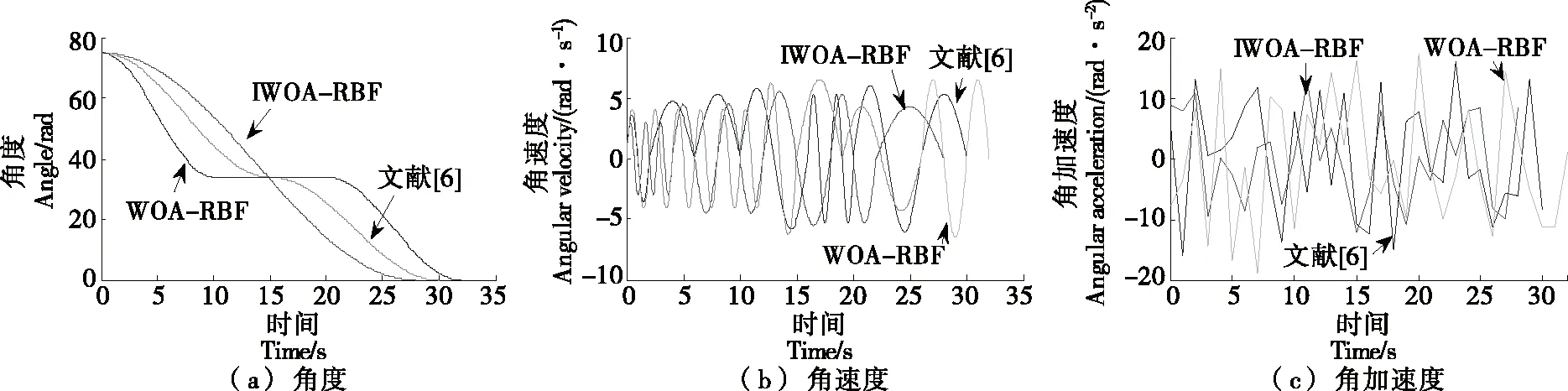
圖6 不同軌跡規劃方法軌跡參數對比

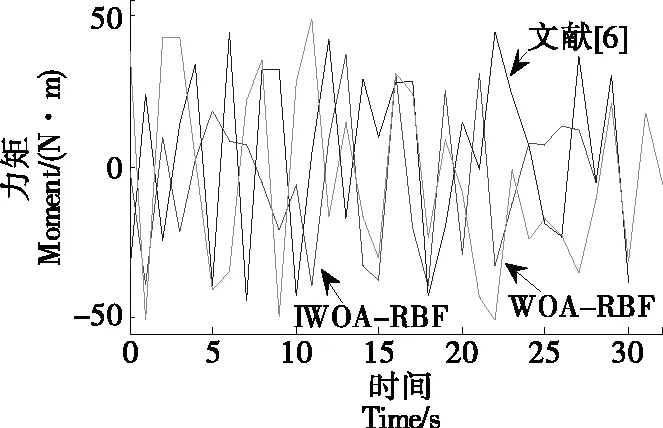
圖7 力矩變化曲線

由圖5可知，相比于其他兩種算法，IWOA-RBF得到的規劃軌跡更平滑，拐點變化更平穩，表明其更適用于關節空間移動。由圖6、圖7可知，對于關節角度位置變化，IWOA-RBF得到的軌跡角位移滿足約束條件，且變化更加平緩；對于角速度、角加速度和力矩，IWOA-RBF的峰值明顯小于其他兩種算法，且IWOA-RBF在力矩峰值時逗留的時間較短，即關節電機處于滿負荷運行的時間短于其他兩種算法，達到了節能的目的。由表3可知，對于同樣的末端起點與終點軌跡規劃問題，雖然IWOA-RBF求解時間不是最短的，但其得到的最優軌跡所消耗的移動時間最短，且軌跡能耗的平均值和最小值均明顯小于其他兩種算法，相比于文獻[6]的能耗結果，平均能耗和最優能耗降低了約15.02%，9.01%，而WOA-RBF表現得最差。

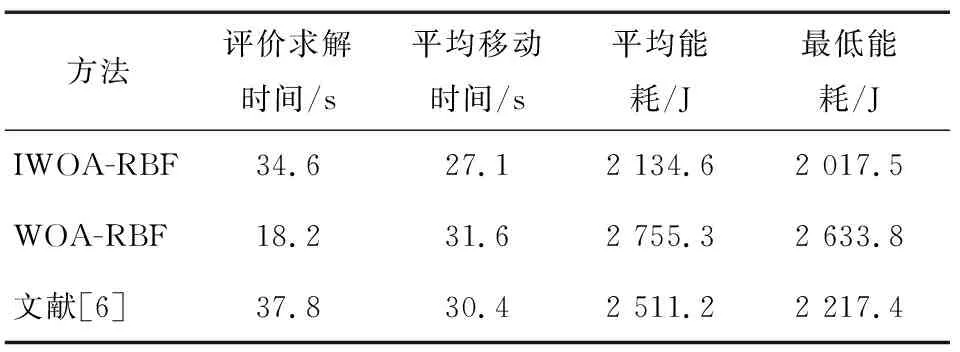
表3 不同軌跡規劃方法指標對比

4 結論

研究提出了一種采用改進徑向基函數神經網絡規劃食品機器人關節軌跡的方法，解決了動力學參數未知情況下的節能軌跡規劃問題，通過引入改進鯨魚算法，提高了徑向基函數神經網絡模型辨識精度，有效降低了關節能耗，該方法能夠應用于食品機器人工作場景。后續將重點研究在線節能軌跡規劃問題，以實現對臨時任務的節能軌跡規劃。