漂浮基空間機器人固定時間收斂主動容錯控制

湯萬興，艾海平, 2，陳力

(1.福州大學機械工程及自動化學院，福建 福州 350108; 2.江西理工大學能源與機械工程學院，江西 南昌 330013)

0 引言

隨著航天科技的發展和人類對外層空間的探索，空間機器人在太空任務執行中被賦予極其重要的地位.特別是近期中國空間站的建成，它被期望能夠扮演更加重要的角色并能執行更為復雜的工作，如將載荷從貨艙移動到指定位置釋放、 捕獲并回收自由飛行的有效載荷、 航天器的對接等，因此, 國內外眾多學者對其研究投入了大量精力[1-4].然而由于在執行這些任務過程中受宇宙射線、 太陽粒子束、 高溫差等惡劣環境特性影響，以及長期運行的需要，機械臂關節容易因老化磨損產生力矩失效故障和在搬運重大負載時發生偏置力矩故障，進而導致系統控制精度下降, 更有甚者，將會對空間機械臂造成損毀.考慮到航天工作的精確性、 穩定性要求及操作難度，對空間機器人進行容錯算法的研究具有重要意義，目前對該算法的研究也已經引起相關學者的重視[5-6].

在空間機器人系統中，機械臂各個關節處驅動連桿按照預定方向運動的伺服電機即執行器受到外界干擾信號、 故障或者由于自身老化磨損等原因，在其自身參數發生變化、 無法完全執行控制器輸出的指令時，可認為執行器發生故障[7]，而在可能發生的執行器故障中，失效故障和偏置故障發生概率最大.針對這兩種故障，空間機器人的容錯控制主要有被動容錯控制和主動容錯控制兩種.其中被動容錯控制是指在不改變控制器結構及參數的前提下，利用魯棒控制技術使整個閉環系統對某些確定的故障具有不敏感性.宋齊等[8]針對漂浮基三桿空間機械臂，結合高階滑模理論，提出一種反演滑模容錯控制.Zhang等[9]針對空間機械臂的失效故障，提出一種自適應固定時間收斂的容錯控制方法.Smaeilzadeh等[10]針對航天器的執行器故障、 外在干擾和模型不確定性問題，提出一種自適應魯棒控制.但是被動容錯控制需要對可能發生的故障進行預判并將預知內容概括到統一的故障模式下，導致設計過程極為復雜且過于保守，不可避免地要損失一定的精度，其性能將不可能是最優的，且若發生不在預知范圍內故障，系統原定要求的動態性能和穩定性將無法保證[11].

相對于被動容錯控制，主動容錯控制對能夠獲取準確的故障信息，在控制器的設計上和對故障的處理上，更為有效和巧妙.主動容錯控制是基于獲得的故障診斷信息對系統進行在線重組的控制策略，其主要設計步驟分為以下兩部分： 1) 設計適當的故障診斷方法，以獲取故障信息； 2) 設計控制器進行在線重構、 重設計和重調度，使系統重新穩定.為克服被動容錯的缺點，Zhong等[12]對遠程控制的空間機械臂單關節卡死故障，提出一種高效的路徑規劃方法，并將控制方法推廣至其他類型的空間機械臂.Chen等[13]對空間機械臂的關節故障提出一種多級監管策略，排查故障機械臂并用正常運行機械臂對期望軌跡進行跟蹤控制，但是上述方法未考慮空間機器人的動力學性能.為解決以上問題，主動容錯控制研究的意義巨大.Milad等[14]針對分數階非線性系統的未知執行器故障和干擾，利用神經網絡和故障診斷技術，設計了兩種自適應故障補償方案.Wang等[15]基于故障診斷和隔離技術，提出一種主動容錯方案用以解決一類非線性系統的傳感器故障.但是考慮到空間機器人的復雜應用場景和其本身的耦合性，上述兩種方案仍然具有其局限性.

考慮到研究現狀，針對空間機器人在搬運載荷過程中受到偏置力矩和力矩失效影響的情況，引入擴張狀態觀測器，對故障進行觀測反饋.相對于其他容錯控制，本方法由于觀測器的使用為控制器處理故障提供了反饋補償數據，無需在設計控制器過程中對所有可能產生的故障進行預判，有效提高系統對故障的處理能力.在此基礎上，設計新型固定時間收斂滑模控制器，保證系統能夠在任意初始狀態下固定時間內收斂，且系統收斂時間可通過調整系統控制參數進行調整.同時控制方法具有非奇異性，進一步提高系統穩定性[16-17].最后進行數值仿真，仿真結果驗證了該控制策略的有效性，相對其他算法其收斂時間更快、 穩態誤差更小、 容錯能力更強、 在故障發生時系統更加穩定.

1 動力學建模

單臂空間機械臂系統如圖1所示，系統為無根多體系統.載體(基座)B0浮動，機械臂由B1、B2和固定在B2末端的載荷P組成，系統位置不受控制.建立系統的慣性坐標系和各分體Bi(i=1, 2, 3)的主軸連體基(Oi,xi)(i=1, 2, 3).其中，Oci(i=1, 2)分別為B1,B2的質心，O1，O2分別為聯結B0與B1，B1與B2的關節轉動鉸的中心.假設系統載體的質量、 轉動慣量及臂長分別為mi,Ji和li(i=1, 2).θ0，θ1和θ2分別為載體姿態轉動角和剛性兩連桿關節轉動角.

空間機器人系統載體(基座)在太空中處于漂浮狀態，具有動力學耦合性.利用拉格朗日法及系統動量守恒原理對不考慮外在干擾、 內在不確定性和機械臂故障的空間機器人動力學方程[18-22]進行推導，可以表示為：

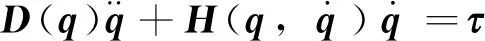
(1)

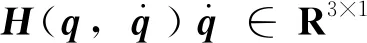
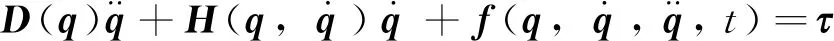
(2)

主要研究力矩偏置故障和力矩失效故障，即關節電機受到一個外在偏置力矩和因系統硬件磨損老化等原因導致的力矩失效故障影響，可將其表示為φ(t)，那么關節實際輸出力矩為：

τ0=[I-ρ(t)]τ+f(t)

(3)

其中：τ為理想輸出力矩；ρ(t)表示力矩失效比例常數；I為單位矩陣；f(t)為偏置力矩.令φ(t)=f(t)-ρ(t)τ，表示故障總和，針對故障φ(t)，提出假設1.

那么可將機械臂動力學系統方程改寫為：

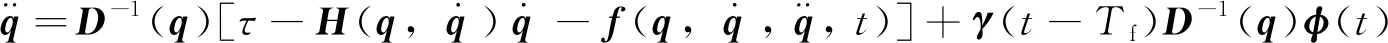
(4)

其中：γ(t-Tf)是一個對稱矩陣；Tf表示故障發生的時間，其表達形式為：

γ(t-Tf)=diag{γ1(t-Tf), …,γn(t-Tf)}

(5)

而γi(t-Tf)表示故障函數，其表達式為：

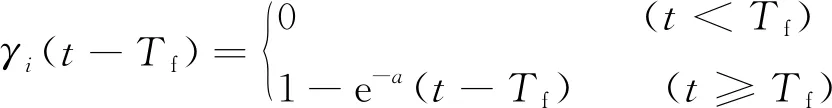
(6)

其中：a>0, 表示故障發生的程度，當a較小時，表示緩變故障，當a較大時，表示突變故障.

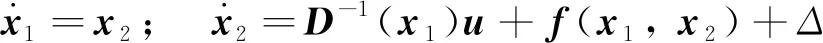
(7)

2 控制方法設計

2.1 觀測器設計

觀測器的設計用于觀測系統可能發生的故障、 外在干擾和內在不確定性的總和，即式(7)中的Δ.根據式(7)和文獻[23]，可將觀測器設計為:

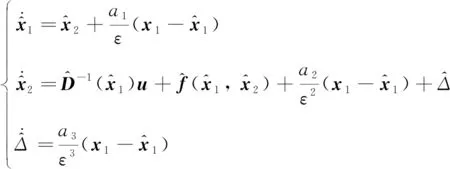
(8)

根據觀測器，可提出定理1.

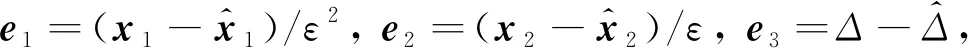
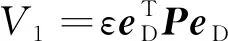
(9)

其中：P為對稱正定矩陣.

根據文獻[24]，對上式求導，可得：

(10)

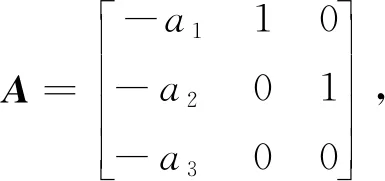
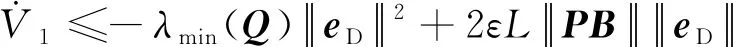
(11)

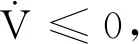
2.2 控制器設計

固定時間收斂原理[17]對于如下標量微分系統：

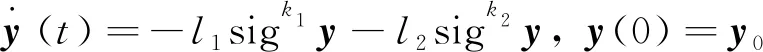
(12)

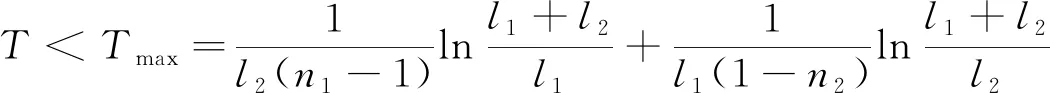
(13)

接下來將根據以上原理設計固定時間收斂滑模控制器.

根據式(7)和(8)，可將系統動力學方程重寫為：

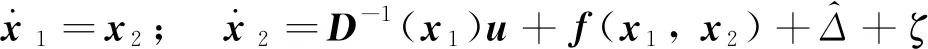
(14)

假設2假設觀測器誤差有界且其上界為Γ，即|ζ|≤Γ.

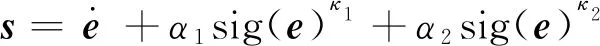
(15)

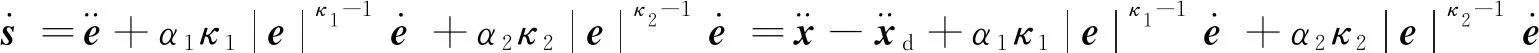
(16)

將式(7)代入其中，可得：

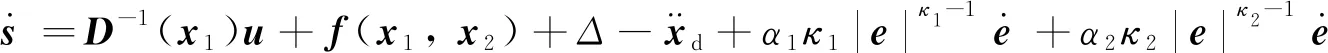
(17)

根據式(17)，可提出控制器：

u=ueq+us

(18)

其中：ueq為等效控制；us為切換控制，且

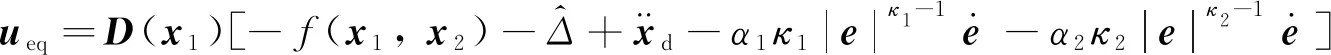
(19)

切換控制可選擇為：

us=D(x1)[-λ1sig(s)γ1-λ2sig(s)γ2-(Γ+υ)sign(s)]

(20)

那么此時可提出定理2.

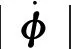
證明 根據以上所述，可設定Lyapunov函數為：

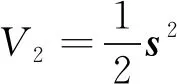
(21)

對其求導，可得：

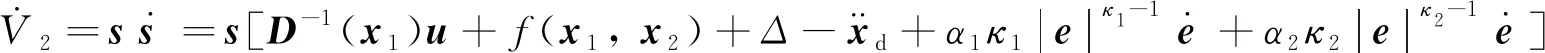
(22)

代入式(18)，可得：

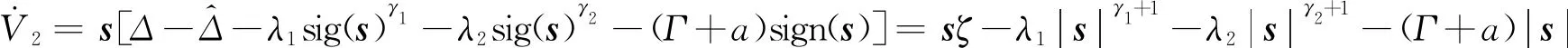
(23)

根據假設1，可得：

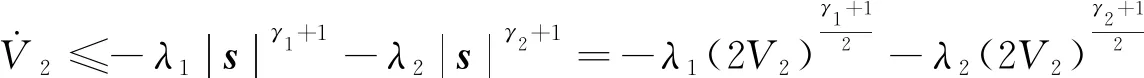
(24)

注意到當V2=0，s也將趨于零.根據固定時間收斂原理，系統將在固定時間內收斂.以下是證明過程.

證明 根據式(24)，V2趨近于零的時間為：

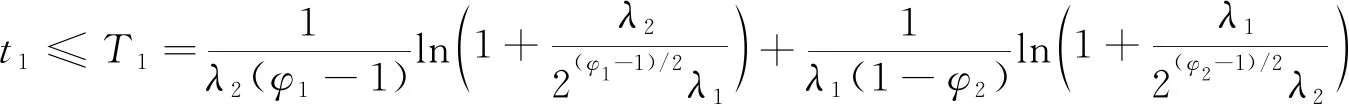
(25)

當V2趨近于零時，s也將趨近于零，此時有：

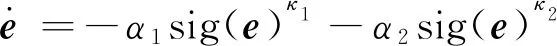
(26)

根據固定時間收斂原理，可知誤差e收斂至零的時間為：

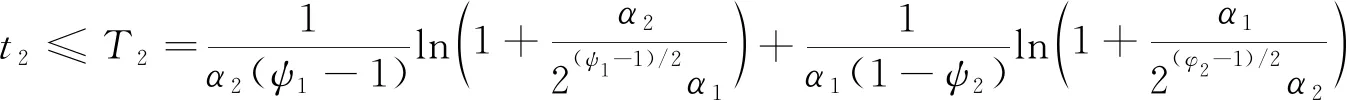
(27)

綜上所述，可知系統收斂時間估計值為：

T≤Tmax=T1+T2

(28)

從時間T的表達式中可知，T的上界與系統的初始狀態無關，而僅與設定的系統參數有關，易知通過改變系統參數，可以調整系統收斂的時間，相對其他算法，這具有極大的優勢.

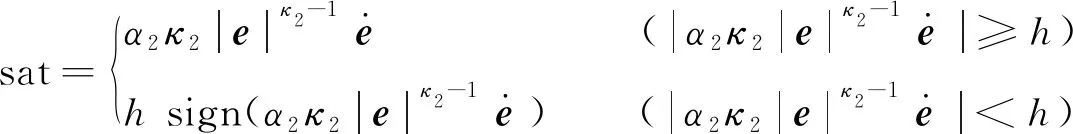
(29)

其中：h為一個大于零的常數.

控制器中的sign(s)項，由于其不連續性，容易導致抖振，這里提出以下函數替代符號函數，以解決抖振問題：

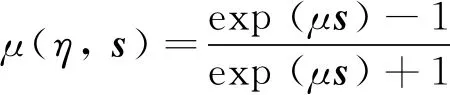
(30)

其中：μ為一個較小的正常數.

3 實驗仿真驗證

為驗證算法的有效性，以圖1所示的漂浮基兩桿空間機械臂為例，將提出的故障觀測器(8)和控制器(18)進行數值仿真，在Malab/Simulink環境中進行計算，采樣時間設為0.001 s，且系統的模型參數設計為：m0=40 kg，m1=5 kg，m2=5 kg，L0=1 m，L1=2 m，L2=2 m，J0=34 kg·m2，J1=1.5 kg·m2，J2=1.5 kg·m2.設空間機械臂載體和關節1、 關節2在關節空間內的期望運動規律為：

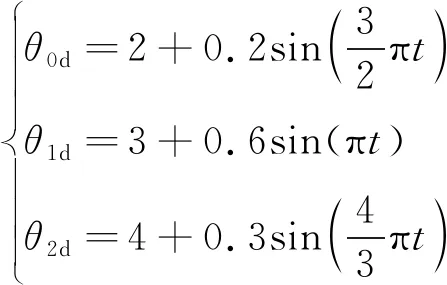
(31)

3.1 觀測器觀測能力驗證

為驗證算法對故障的處理能力并展示故障觀測器對故障的觀測能力，設定空間機械臂不存在外在干擾和摩擦項，即f(t)=0，此時觀測器觀測結果便只有故障項.

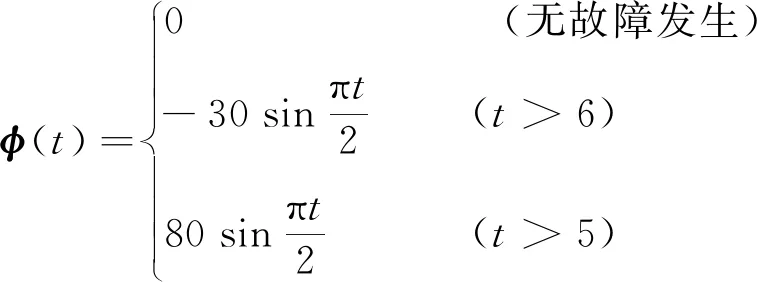
(32)

其中:φ(t)=0表示沒有故障發生，載體正常運行； 第6秒起關節1受到力矩偏置故障的影響，φ1=-30 sin(πt/2)； 第5秒起關節2受到力矩偏置故障的影響，φ2=80 sin(πt/2).

故障觀測結果如圖2所示.由于觀測器是基于狀態量更新迭代設計的，狀態量之間存在動力學耦合作用.由圖2可知，當關節1觀測到第5秒關節2故障出現時，會聯動導致關節1的故障觀測產生一定的浮動； 但當第6秒關節1故障出現之后，關節2在第5秒出現的浮動被很快穩定，且觀測器對故障進行了很好的跟蹤觀測.由此可知，觀測器的使用可對故障進行觀測反饋，提高了系統的魯棒性或容錯性能.

3.2 控制器能力驗證

表1 控制器控制參數

假定系統受到發送故障項及干擾項等多重因素影響，為了表明所提算法的主動容錯能力，采用上述算法進行仿真，仿真結果為機器人各關節誤差.故障項和集成干擾項如下式所示：

3種控制器軌跡跟蹤誤差如圖3所示.從圖3可知，存在干擾的情況下，與其他3種算法相比，本算法控制效果最好.圖3(a)顯示在無故障情況下，本算法穩態誤差最小，反映了本算法較好地控制性能； 圖3(b)顯示關節1在第6秒偏置力矩故障發生之后，PIDSMC和CTC控制方法的穩態誤差曲線都發生了較大的浮動，系統控制無法保持較好的穩態控制效果，但AFTC的誤差曲線在短暫的浮動之后繼續收斂，而FxSMC的誤差曲線則幾乎沒有浮動； 從圖3(c)中可以看出，關節2發生力矩偏置故障和失效故障之后，CTC算法誤差驟增，PIDSMC算法誤差曲線發生一定波動，AFTC誤差曲線浮動較小，而FxSMC算法誤差并未發生較大波動，進一步展示了FxSMC算法的優越性.

4 結語

針對空間機器人在搬運重大載荷過程中受到偏置力矩和由于關節老化磨損產生的關節力矩兩種失效故障影響的情況，基于固定時間收斂滑模設計了滑模控制器，并引入一類擴張狀態觀測器，設計一種主動容錯控制方法，對系統故障進行在線識別檢測以提高系統控制的精確度.本算法設想使用觀測器之后能夠使系統具有主動容錯能力, 固定時間收斂原理使其具有更快的收斂時間.為驗證算法的理論可靠性，將本算法與其他3種算法進行對比，結果證明本算法理論具有可行性，在控制精度、 響應速度和穩態誤差各項指標上均有所改善.在容錯能力的對比上，本算法在受到力矩失效故障和力矩偏置故障的影響時，所受影響較小，系統誤差保持在較小范圍內且無大幅波動，表明其具有較優的容錯性能.