摻復合鎳鐵渣混凝土梁柱中節點變形特性

陳尚鴻，祁皚，劉旭宏，黃增楠，林偉

(1.福州大學土木工程學院，福建 福州 350108；2.福州大學土木工程防震減災信息化國家地方聯合工程研究中心，福建 福州 350108)

0 引言

目前，我國每年在鎳鐵合金冶煉生產中排放出的鎳鐵渣在3 000萬t以上，已成為我國第四大冶煉工業廢渣[1-2], 開發利用鎳鐵渣具有重要意義.鎳鐵渣可與水泥發生二次水化反應用以生產混凝土[3-4].文獻[5-8]已分別對復合鎳鐵渣混凝土的基本力學特性、 與水平鋼筋的粘結特性、 梁的受彎承載力和變形特性、 梁柱節點的承載力進行了研究.復合鎳鐵渣為福建源鑫集團商業化生產的一種復合礦物摻和料，按鎳鐵渣∶礦渣=2∶1研磨至細粉.研究發現： 在復合鎳鐵渣混凝土與普通混凝土抗壓強度相等的情況下，二者的基本力學特性相同，與具體復合鎳鐵渣摻量無關[5]； 但隨著復合鎳鐵渣摻量增加，泌水效應凸顯，逐漸削弱了復合鎳鐵渣混凝土與水平鋼筋之間的粘結性能[6].復合鎳鐵渣混凝土與梁縱筋之間相對較小的粘結強度不影響梁的受彎承載力和變形特性[7]，但會使梁柱節點核心區內梁貫穿縱筋的粘結錨固力降低，需采取梁縱筋相對貫穿長度限值的措施[8].

基于前人的試驗數據，本文對摻復合鎳鐵渣混凝土梁柱中節點(后簡稱“鎳渣砼中節點”)的變形特性進行進一步研究，以期為復合鎳鐵渣混凝土在普通框架結構中的應用提供一定借鑒和參考.

1 試驗概況

1.1 材料及試件信息

文獻[9]已對4個半預制鎳渣砼中節點進行梁端加載的滯回試驗研究，試驗參數為復合鎳鐵渣摻量.試件所用混凝土配合比、 鋼筋材性、 試件信息及加載方式見表1～2和圖1.表1中，β、η分別表示每立方米混凝土中的復合鎳鐵渣摻量、 減水劑摻量占比；mw、mc、mf、ms、mg分別表示每立方米混凝土中的水、 水泥、 復合鎳鐵渣、 砂、 石的質量；fcu表示混凝土28 d齡期立方體抗壓強度.表2中，Es、fy、fu分別代表鋼筋的彈性模量、 屈服強度、 極限強度.試件的軸壓比均取0.1.試驗全程采用以位移控制的加載制度，分為彈性和屈服兩階段，如圖2所示.在彈性階段，試件的開裂荷載對微小位移變化敏感，因此，僅施加很小的初始位移，并逐漸增大所施加的位移，每級加載只循環一次.當鋼筋屈服或荷載-位移滯回曲線出現明顯拐點時，試件進入屈服階段，此后，施加的位移荷載為屈服位移的倍數，每級加載循環兩次.當試件的承載力下降至記錄的最大承載力85%時，即終止試驗.試驗的其他細節，參考文獻[9].

表1 試件混凝土配合比

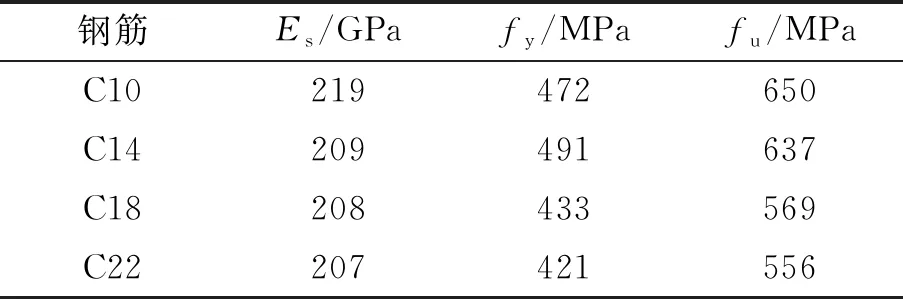
表2 鋼筋材性

1.2 主要試驗結果

試件最終的破壞現象均為梁端受壓區混凝土大面積剝落，柱體保持完整，并伴有節點核心區輕微“X”形裂縫，典型試件破壞現象見圖3.各試件梁端荷載-位移骨架曲線如圖4所示.JD1、 JD2、 JD3、 JD4的梁端加載點平均極限位移分別為42、 56、 50、 51 mm，這是由于不同強度等級混凝土脆性不同及不同混凝土與梁縱筋之間粘結力大小綜合影響的結果.需要進一步采用理論和數值分析方法研究混凝土與梁縱筋粘結強度降低，即復合鎳鐵渣摻量增多對節點整體變形的影響.因為混凝土脆性特征主要與強度有關，而與復合鎳鐵渣摻量無關[5]，因此，本文不對混凝土脆性因素展開分析.

2 鎳渣砼中節點變形分析

2.1 中節點變形的構成

梁端加載點的位移Δ由以下幾部分構成，即

Δ=Δb+Δc+Δx+Δs

(1)

式中：Δb、Δc分別表示由梁體、 柱體彎曲變形產生的梁端加載點位移；Δx表示由節點核心區剪切變形產生的梁端加載點位移；Δs表示由梁柱界面處鋼筋滑移產生的附加轉角對梁端加載點位移的貢獻.各變形分量對梁端加載點位移的貢獻如圖5所示.

在試件最終破壞時，柱體保持完整.按結構力學基本知識估算，在極限狀態，Δc僅為0.7 mm，可以忽略不計.按文獻[9]中的試驗數據，節點核心區的剪切變形最大值為0.003 rad左右，換算為Δx約為1.8 mm，同樣忽略不計.為達到較高的分析效率，式(1)簡化為下式.

Δ=Δb+Δs

(2)

式(2)是以“強柱弱梁”及“強節點、 弱構件”設計原則為前提的，本文所有分析及結論均建立在這一前提上.在文獻[7]中，已經論證了復合鎳鐵渣摻量(即梁縱筋粘結力削弱)對梁體變形Δb沒有影響，本文后續僅分析復合鎳鐵渣摻量對Δs值的影響.

2.2 復合鎳鐵渣摻量對梁柱界面附加轉角變形的影響

在梁柱界面處的梁受拉縱筋屈服后，隨著梁截面彎矩的增大，縱筋將進入強化階段，應力、 應變會繼續增大.隨著應變滲透[10]進入節點區、 梁內，受拉縱筋與節點區、 梁內的混凝土之間就會產生相對滑移，引起梁柱界面的張開而形成此區域的附加轉動θs，如圖6所示.當節點區無法提供足夠的粘結錨固力以抵抗梁縱筋逐漸增長的拉力時(即梁縱筋屈服應變滲透進全節點區)，其錨固將逐漸轉移到該節點另一側的梁內[11].梁柱界面張開大小δs(梁縱筋總滑移量)由梁內和節點內的縱筋滑移量疊加組成，根據文獻[12]的相關理論推導，得到下式.

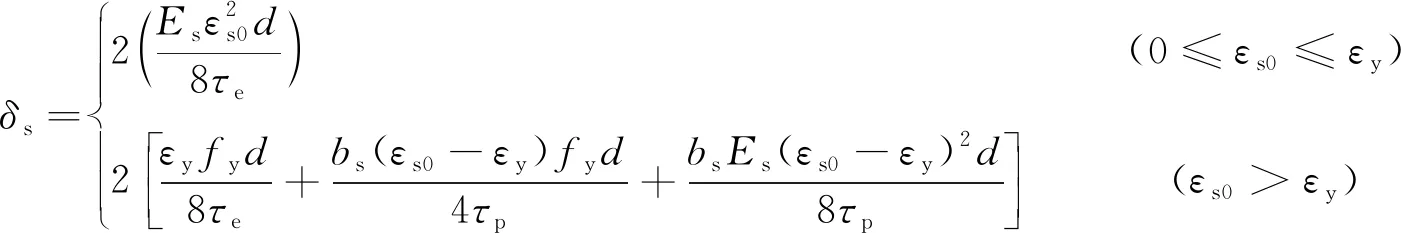
(3)

式中：Es為鋼筋彈性模量；d為梁縱筋直徑；εs0為梁柱界面處梁縱筋的應變;εy為鋼筋屈服應變；fy為鋼筋屈服應力；bs為鋼筋硬化率；τe、τp分別表示梁縱筋屈服前后兩階段粘結應力.

根據文獻[6]和[12]，對于復合鎳鐵渣混凝土，τe和τp可表示為：

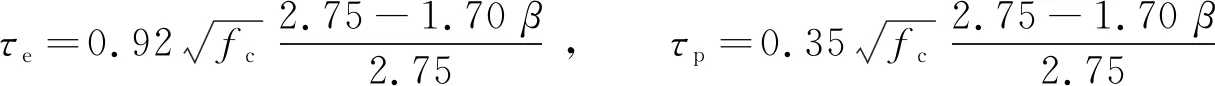
(4)

式中：fc為復合鎳鐵渣混凝土軸心抗壓強度；β為復合鎳鐵渣微粉摻量(質量分數)，%.

θs可表示為

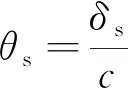
(5)

式中：c為受拉縱筋至中性軸的距離.

結合式(3)～(5)可以看出，在鋼筋材性一定的情況下，隨著τe、τp值降低，即隨著復合鎳鐵渣摻量增多，梁柱界面附加轉角變形增大.Δs可按下式進行計算.

Δs=θs·Lb

(6)

式中：Lb為加載點到梁柱界面之間的距離.

3 數值分析

3.1 基本方法

基本假定有： 平截面假定； 彎矩沿梁體呈線性分布； 鋼筋應力-應變關系采用雙折線模型，鋼筋硬化率取0.01，忽略混凝土拉應力； 當受拉鋼筋達到屈服應變時，將此時的截面曲率定義為屈服曲率，當受壓區混凝土最外層纖維受壓應力下降至混凝土受壓峰值應力0.1倍以下時，將此時的截面曲率定義為極限曲率.復合鎳鐵渣混凝土纖維的受壓應力-應變關系參見文獻[5].

節點變形計算的主要步驟可歸納為8步： ① 以εs0為基本變量，并設定增量步； ② 根據式(3)～(6)，計算與εs0相對應的Δs0； ③ 采用纖維截面法[13]計算梁柱界面處的截面彎矩M0、 截面曲率φ0； ④ 根據M0，確定相應的梁端加載力F0； ⑤ 根據梁上的線性彎矩分布，確定相應的曲率分布，通過數值積分確定與εs0相對應的Δb0； ⑥Δ0=Δb0+Δs0； ⑦ 判斷最外層受壓混凝土纖維應力是否小于0.1倍峰值應力，是則退出計算； ⑧ 得到(F0-Δ0)曲線.

3.2 結果及參數分析

采用節1的試驗結果對比驗證本文數值方法的準確性，如圖7所示，各試件的數值計算曲線與試驗骨架曲線基本吻合，說明本文所采用的數值計算方法是相對準確的，可進一步用于變參數的數值分析.

文獻[5]已對復合鎳鐵渣混凝土C30FX、 C35FX系列進行了詳細的材性試驗研究，其中，FX代表復合鎳鐵渣摻量為X%.在此設置兩個數值計算分析對比組.各對比組中試件尺寸、 配筋、 加載位置均與圖1相同.數值計算分析結果如圖8所示.

從圖8可看出，同一對比組內，隨著復合鎳鐵渣摻量的增多，梁端的極限位移逐漸增長.另外，第二對比組構件的整體位移略比第一對比組小，這是第二對比組中混凝土脆性較大的原因導致的.

進一步分析在構件屈服狀態和極限狀態時Δs和Δb分別對整體變形的貢獻比例，如圖9所示.可以看出，Δs占構件整體變形的比例較高.在構件屈服狀態及之前，Δs占比為30%～45%，而到了極限狀態，Δs占比上升到了50%～65%.在一些前人學者的研究中也發現了類似規律，例如，徐云扉[14]試驗考察了一榀1/2縮尺比例的三層兩跨RC框架的抗震性能，結果表明，在中柱節點內由梁縱筋粘結滑移所產生的轉角變形約占梁端塑性鉸區總轉角變形的35%.在圖3中，在極限狀態下，梁的上、 下外輪廓線幾近直線，梁柱界面附加轉角變形明顯，間接反應出Δb的變形量并不顯著.從參數變化上來看，同一組內，隨著復合鎳鐵渣摻量增多，Δs占比逐漸增大，這是因為混凝土與梁縱筋粘結力減小導致梁柱界面附加轉角增大的緣故.

4 梁端等效塑性鉸模型

理論上講，RC受彎構件極限變形能力可采用數值方法，但計算較為復雜，工程設計中一般采用簡化方法——等效塑性鉸模型[15].如圖10所示，在極限彎矩Mu作用下，RC受彎構件上的實際曲率沿長度L為非線性分布.將其簡化，認為實際極限曲率φu分布由沿構件全長線性分布的屈服曲率φy和在等效塑性鉸長度Lp范圍內均勻分布的塑性曲率φp疊加而成.則構件頂點極限位移Δu可由下式[16]計算.

(7)

式中：Δy、Δp分別表示構件頂點的屈服位移和塑性位移.

在“強柱弱梁”、 “強節點、 弱構件”設計原則下，可實現節點梁鉸破壞機制，變形均集中于梁鉸內.因此，可以建立梁端等效塑性鉸模型，以預測鎳渣砼中節點的極限變形.塑性鉸長度需要同時考慮梁彎曲效應和梁柱界面處鋼筋滑移效應，即公式中要涵蓋L、β和d項.對于節點試驗，L(梁長)指梁端加載點至梁柱界面之間的距離(前文Lb)，對于實際框架結構，指梁反彎點至梁柱界面之間的距離.由于，在目前實際建筑工程中，常用鋼筋等級為HRB400，本文將此作為應用前提，塑性鉸長度公式中將不再以fy作為變量.本文提出的塑性鉸長度的表達式：

Lp=λ1L+(λ2β+λ3)d

(8)

式中：λ1, 2, 3為待定系數.

為確定待定系數λ1, 2, 3，就需要一定量的數據庫用于擬合.由于大節點試驗的花費是昂貴的，因此，本文采用數值方法建立該數據庫.采用的節點試件原型與第1節相同，混凝土強度等級為C30、 C35，選取的變量有β(0%、 30%、 50%)、L(1 200、 2 000、 3 000 mm)、d(18、 20、 22、 25 mm).各參數取值互相組合，計算結果，以建立該數據庫(Li,βi,di, (Δu)i, (φy)i, (φu)i, (φp)i, …).

將式(7)變形為式(9).

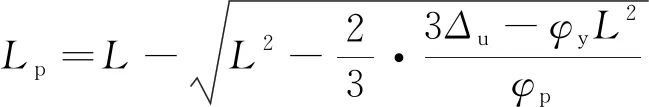
(9)

通過式(9)和計算得來的數據庫，可以得到不同參數(L、β、d)下的Lp值，這是采用數值計算方法得到的.采用式(8)對Lp值進行擬合，可以得到式(10).

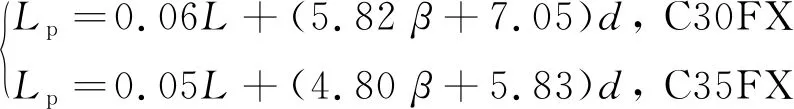
(10)

經過驗算，式(9)與式(10)之間的計算誤差均小于5%.通過計算得到的數據庫結果，可近似將φy、φu、φp擬合為下式.

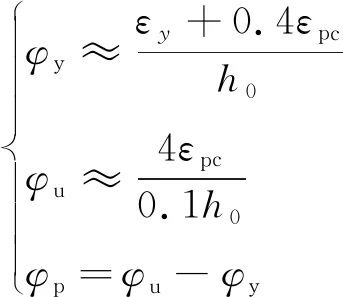
(11)

式中：εpc為混凝土峰值壓應變；h0為梁截面有效高度.

結合式(10)～(11)便可快速地計算鎳渣砼中節點的極限變形或塑性轉角(Lp、φp).可以看出，當β、d值增大時，塑性鉸長度增大，即節點的變形能力增強.因為，β值增大，梁縱筋與復合鎳鐵渣混凝土之間的粘結力降低，有利于梁縱筋產生滑移； 另外，梁縱筋的拉力與d2值成正比，梁縱筋與混凝土的粘結錨固力僅與d值成正比，d值增大也將有利于梁縱筋產生滑移.實際上，β、d值的增大提高了梁柱界面的附加轉動能力.

5 結語

1) 對鎳渣砼中節點的試驗研究發現，梁體的受彎變形并不明顯，而梁柱界面附加轉角變形明顯.

2) 從數值計算分析中發現，隨著復合鎳鐵渣摻量的增加，節點梁柱界面處附加轉角變形逐漸增加，占整體變形相當大的比例.在構件屈服狀態及之前，Δs占比為30%～45%，而到了極限狀態，Δs占比上升到了50%～65%.

3) 提出鎳渣砼中節點梁端等效塑性鉸模型，確定塑性鉸長度與梁長、 復合鎳鐵渣摻量、 梁縱筋直徑之間的關系.可以快速確定鎳渣砼中節點的極限變形能力.