一階全偏聯系數的計值公式及其應用
劉宗寶 LIU Zong-bao;陸廣地② LU Guang-di;趙克勤 ZHAO Ke-qin
(①江蘇聯合職業技術學院宿遷經貿分院,沭陽 223600;②江蘇科技大學計算機信息與技術學院,鎮江 215600;③諸暨市聯系數學研究所,諸暨 311800)
0 引言
系統是客觀存在的,具有普遍性。從系統組成要素的性質來看,可以劃分為自然系統和人造系統。自然系統是由自然物組成的,它的特點是自然形成的,如生態系統、星際系統等;人造系統是人們出于某種目的而制造的系統,如生產系統、交通系統、商業系統、管理系統等。還有從系統與環境的聯系程度來看,可以劃分為封閉系統和開放系統;從系統的狀態與時間的關系來看,可以劃分為靜態系統和動態系統等等。無論是何種分類的系統,它們都具有以下幾個共同的特征:整體性、層次性、目的性和適應性。系統總是在相互合作和不斷演化的過程中呈現的耗散結構。長期以來科技工作者總是嘗試捕捉大千世界的變化過程和演化強度,在變化的過程中把握其中的不變性。我國學者趙克勤先生1989年創立的集對分析理論為這方面研究提供了新思路;用一個聯系數刻畫一個系統中部分要素正常、部分要素異常、部分要素反常的狀態,簡稱同異反系統。聯系數的偏聯系數是刻畫這個系統部分要素正常、部分要素異常、部分要素反常這三部分之間相互遞進和衰減演化的伴隨函數,目前已得到廣泛應用,如覃杰、趙克勤(2007)將偏聯系數應用于醫療質量發展趨勢分析,王傳斌、王繼順(2011)將偏聯系數應用于對高職教師執行力的潛在分析,馬曉燕等人(2012)將偏聯系數應用于公眾信任度潛在分析,陸廣地等(2015)將偏聯系數應用于高校評價的排序與聚類分析,晏燕等(2018)把偏聯系數用于隱私風險態勢評估,門寶輝(2022)將偏聯系數應用于地下水開采評估,陳微,趙克勤(2022)將偏聯系數應用于學生近視分析,楊紅梅(2019)給出了多元聯系數的偏聯系數計算方法,于2021年出版專著《偏聯系數的哲學原理與應用》等。但三元聯系數的一階全偏聯系數中含有不確定性示性系數i和i,如何根據問題的已知條件客觀地給定i和i的值,直接影響到一階全偏聯系數的計算結果和聯系數系統的演化趨勢判定。趙克勤(2005)、楊紅梅(2019、2021)、陸廣地(2022)相繼給出了不同的取值方法。但是最近的研究表明,三元聯系數的一階全偏聯系數的不確定性示性系數i和i還存在新的算法,本文給出了這一新算法的原理,進而給出了三元聯系數的一階全偏聯系數計值公式,用實例說明這一新公式的應用。
1 三元聯系數及其一階全偏聯系數計值公式
1.1 三元聯系數
三元聯系數是集對的一種特征函數,其一般形式為μ=a+bi+cj,其中a、b、c∈[0,1],i∈[-1,1],j=-1,μ∈[-1,1](1)
由(1)式知,聯系數具有以下性質。
<性質1>系統性。聯系數μ包含a,bi,cj3個聯系分量,且分別處于+1,[-1,1],-1三個層次,“+”號表示a,bi,cj具有3個層次的空間聯系,i是b的示性系數,表明b的取值具有不確定性,j是c的示性系數,表示c與a具有正負對立性,在忽略不計i、j的示性系數意義時,“+”號表示單個聯系分量與三元聯系數整體的聯系;a,bi,cj分別稱為三元聯系數的同部、異部、反部。
<性質2>可計算性。從數學角度看,式(1)是一種結構函數,具有可計算的特點:既可以用來表征一個現實系統既有確定性測度a和c,又有不確定性測度bi的狀態,又可借助適當的伴隨函數,展示式(1)聯系數所示系統狀態的演化趨勢。
1.2 三元聯系數的偏聯系數
由文獻[3]知,三元聯系數的偏聯系數由趙克勤先生于2005年提出,其概念的形成和相應的計算規則主要依據聯系數的上述2條性質。具體又分成三元聯系數的一階偏正聯系數和三元聯系數的一階偏負聯系數,以及三元聯系數的一階全偏聯系數,這些概念用如下3個定義體現。
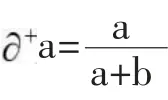
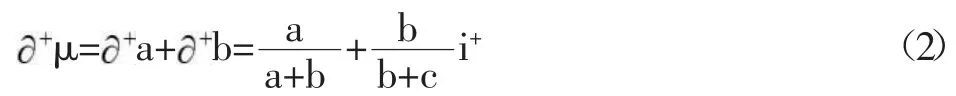

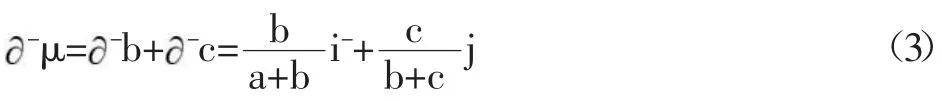

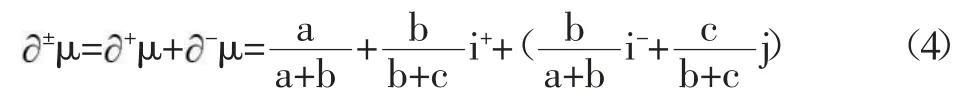
以上式(4)中,j=-1是式(1)所示三元聯系數μ=a+bi+cj在正負型對立問題中規定的取值,但i與i如何在i的定義域[-1,1]中取值,則是一個有待于進一步具體分析的復雜問題。
1.3 i與i的取值
趙克勤先生在2022年8月6-10日網絡在線舉辦的全國集對分析第16次學術研討會上提出了(5)式中i與i的一種新算法如下:
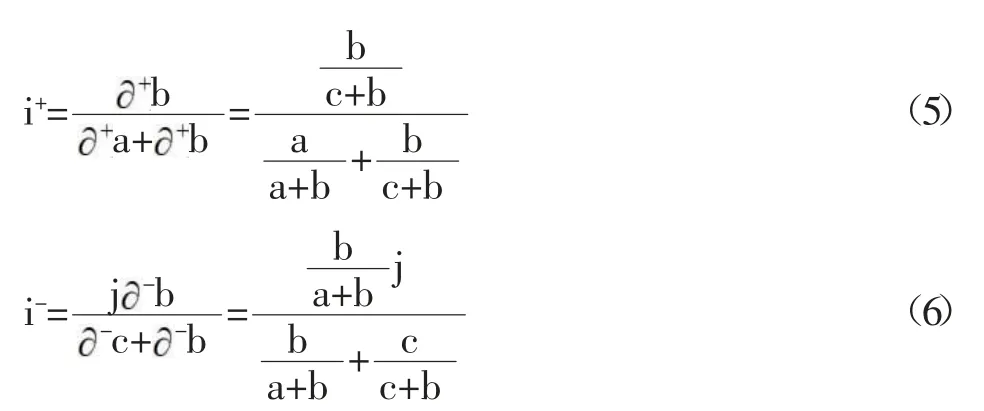
原理如下:
把(4)式所示的三元聯系數μ=a+bi+cj的一階全偏聯系數簡化為具有正極和負極兩個極性的一個線性系統S^。

圖1 線性系統的兩種工作狀態(正常+1與反常-1)表示


圖2 線性系統SAC^分解成兩個子系統SAB^和SBC^的圖示
再把圖2(1)與(1)式相比較,其演化分量的關系可以用如圖3(1)所示。

圖3 線性系統SAC^分解成兩個子系統SAB^和SBC^的演化分量圖示
根據量子糾纏、對立互補的思想,系統表面層是從B向A方向運動,但其微觀層是伴隨對立狀態,i起調節作用,所以i在微觀上遵從A向B作反向運動,按照其運動方向的“比例原則”進行計算。由圖3(1)可知i應該按照上式(5)進行計算。
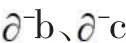
需要指出的是,式(6)中的分子中給出示性系數(jj=-1),體現了式(6)的絕對值是其演化內容包含為反方向時的強度;至于式(5)中的i本來是正向,所以不必要添加表示正方向的示性系數+1。
把式(5)式(6)代入式(4),得到

2 應用舉例
例:為了便于對照,這里引用文獻[7]中的例題,其原始數據全部在文獻[14]中,是我國曾經的985工程建設高校中的8所學生滿意度調查數據處理成標準化的三元聯系數之后,再按照本文的公式(2)(3)聯系數處理如表1所示。
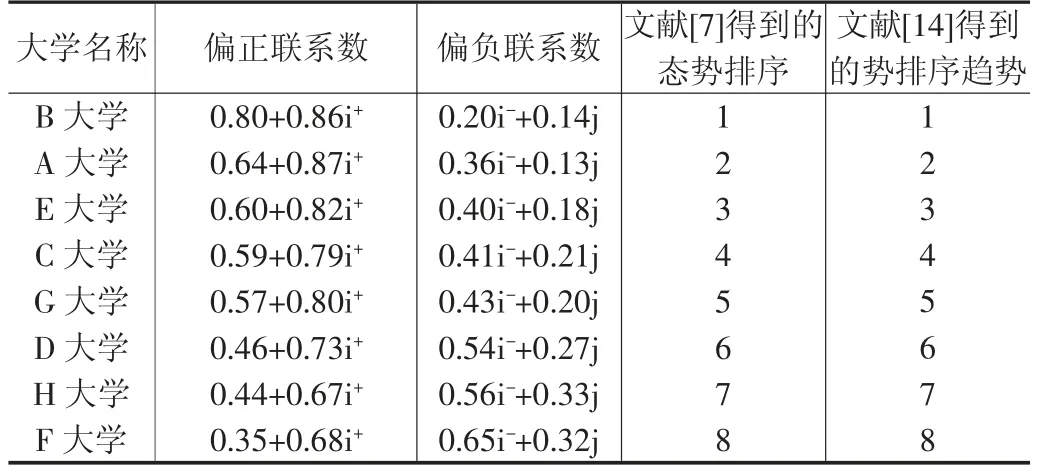
表1 學生對8所著名高校本科教育評價滿意度的偏聯系數態勢排序
將表1中聯系數中i與i使用本文給出的算法代入算出偏正聯系數、偏負聯系數,按照公式(4)求出全偏聯系數值,再據其值進行態勢排序,與文獻[14]進行比較,如表2所示。
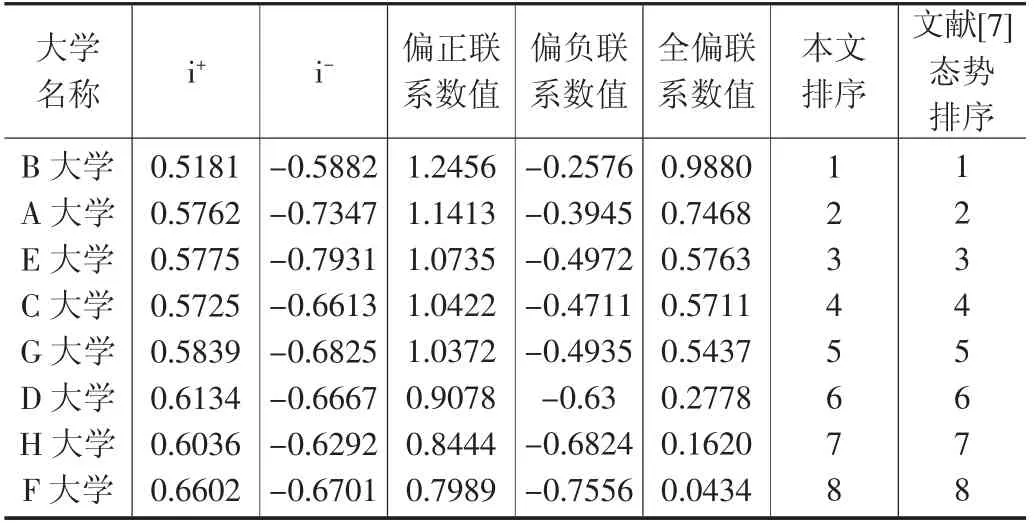
表2 學生對8所著名高校本科教育滿意度的偏聯系數中i+、i-按本文取值的態勢排序
從表2可以清楚地反映出,本文對i和i的新方法與文獻[7]的態勢排序具有內在的一致性,差別在于文獻[7]把三元聯系數μ=a+bi+cj中的i看成是不確定性聯系分量b的示性系數,本文則從三元聯系數μ=a+bi+cj整體角度對i取值,殊途同歸,相互證明了兩種取值方法的科學性。
3 討論與結論
3.2 結語 本文給出三元聯系數的一階全偏聯系數計值公式及其原理,用實例說明其應用的有效性。但三元聯系數已應用到水文水資源、地質礦山、交通物流、社會經濟等不同領域,不同領域不同問題中的三元聯系數有不同的物理意義,如何根據不同領域不同實際問題要求計算三元聯系數的一階全偏聯系數數值,需要不同領域專家根據不同問題要求從不同角度探索,本文提出的的計算公式僅作為一家之言,作為引玉之磚供有關專家參考。

