Tunable second-order sideband effects in hybrid optomechanical cavity assisted with a Bose–Einstein condensate
Li-Wei Liu(劉利偉) Chun-Guang Du(杜春光) Guo-Heng Zhang(張國恒) Qiong Chen(陳瓊)Yu-Qing Shi(石玉清) Pei-Yu Wang(王培煜) and Yu-Qing Zhang(張玉青)
1College of Electrical Engineering,Northwest Minzu University,Lanzhou 730000,China
2Visiting Scholar,Department of Physics,Tsinghua University,Beijing 100084,China
3State Key Laboratory of Low-Dimensional Quantum Physics and Department of Physics,Tsinghua University,Beijing 100084,China
4School of Physics and Electronics Science,Hunan University of Science and Technology,Xiangtan 411201,China
Keywords: second-order sideband,Bose–Einstein condensate,cavity optomechanical
1. Introduction
Cavity optomechanical system(COMS)describes the interaction between the radiation pressure and mechanical degrees of freedom, which has been developing rapidly in recent years.[1–3]These COMS can induce exciting phenomena,such as optomechanical-induced transparency (OMIT),[4–7]slow and fast light,[8,9]optical bistability,[10–13]higher-order sidebands (HS),[14–19]sideband comb,[20–23]optomechanical chaos,[24–26]quantum entanglement,[27,28]and so on. Some phenomena can be explained by the linearized optomechanical interactions, while the others need to be explained by the nonlinear interactions. In recent years,the second-order sideband(SS)or even HS effect induced by the nonlinear optomechanical interactions have attracted much attention. However, SS and HS effects are generally much weaker than the detected signal, it is difficult to detect or exploit in COMS.Therefore, generating and amplifying the SS and HS become an essential task in many physical fields, including precision measurement of DNA molecules properties,[29]precise sensing of charges[30–32]and mass,[33]weak force and single particle detection,[34,35]excellent optical frequency combs,[36–39]and so on.
There are many COMS that share the same properties,such as Fabry–P′erot cavity with moving end mirror or a membrane in the middle,[40–47]and a Bose–Einstein condensate(BEC) trapped inside an optical cavity.[48–53]Great progress has been made in the study of various characteristics of a hybrid COMS composed of BEC, such as quantum entanglement generation,[54–57]quantum ground-state cooling,[58–61]coherent quantum noise cancelation,[62,63]Fano resonances and OMIT with single and multiple windows,[64–66]quantum router,[67]and so on.
In this paper,we study the tunable SS effects in a hybrid COMS, where a cigar-shaped BEC is trapped inside an optical cavity with a moving end-mirror.[68]In our model, the laser field in the cavity has two functions: it excites the momentum side mode of the BEC, and the cavity mode will act as a spring between ultra-cold atoms of BEC and mechanical resonator and couples the motion of both.[6]In Section 2,we give the Hamiltonian of the hybrid COMS consisting of a BEC with s-wave scattering interaction trapped inside a cavity with a moving end mirror under the condition of discrete mode approximation. We derive the analytic expression of the transmission intensity|tp|2of the probe field and the dimensionless amplitudeηsof the SS by the quantum-Langevin equations.Because of the atom–atom interaction,the interaction between atoms–cavity can be enhanced by the atoms collectively couple to the same optical cavity.[49,50]Moreover, the frequency of the Bogoliubov mode depends on the s-wave scattering frequencyωsmof the atomic collision, we can obtain the controllability of the frequency of the Bogoliubov mode by the swave scattering interaction.[69,70]The numerical results show that the effect of the transmission intensity and the dimensionless amplitude of the SS can be controlled effectively by the control field intensities, the nonlinear atom–atom interaction,the effective detuning, the effective coupling strength of the optical field with the Bogoliubov mode in Section 3. Finally,our summary is given in Section 4.
2. System and method
The hybrid COMS we considered is shown schematically in Fig. 1, consisting of a cigar-shaped BEC ofNtwolevel atoms with massmaand transition frequencyωainside a single-mode, high-finesse Fabry–P′erot cavity with lengthLwhose end mirror is free oscillated with frequencyωm. The cavity field is driven by a strong pump laser field with frequencyωpuaccompanying a weak probe laser field with frequencyωprthrough one of its mirror. We assume the BEC to be confined in a cylindrically symmetric trap with a transverse trapping frequencyω⊥and negligible longitudinal confinement along thexdirection.Then we can describe the dynamics within an effective one-dimensional model by quantizing the atomic motional degree of freedom along thexaxis only. Furthermore,the laser pump is far detuned from the atomic resonance,i.e.,Δa=ωpu-ωa?γa,hereγais the atomic linewidth,then the excited electronic state of the atoms can be adiabatically eliminated and spontaneous emission can be neglected,so the atomic wave function can be described by the scalar quantum fieldΨ(x).[60]The Hamiltonian can be written as
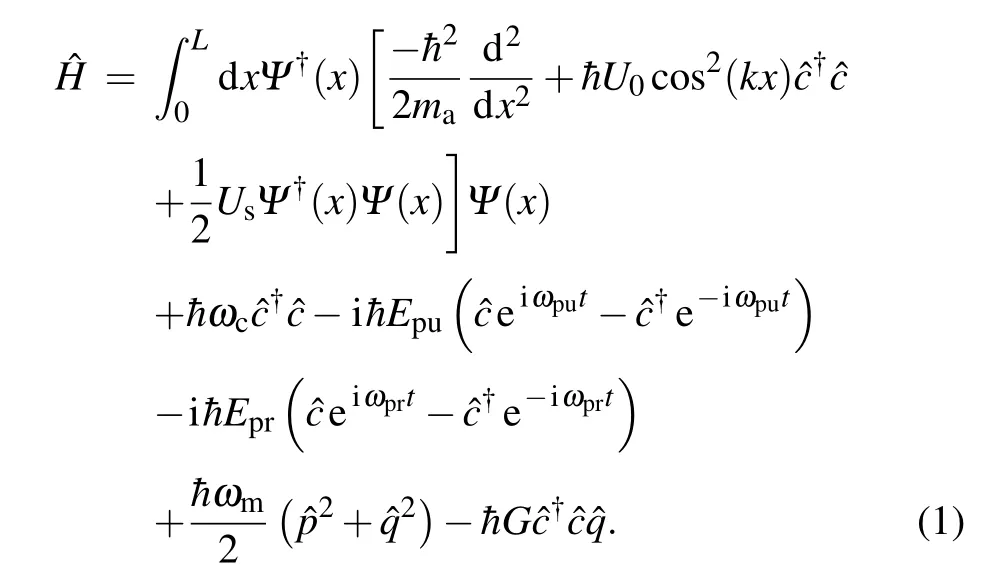


Fig. 1. The hybrid optomechanical system consisting of a BEC trapped inside an optical cavity with a moving end-mirror. The cavity is driven by a strong pump laser with frequency ωpu and a weak probe laser with frequency ωpr.
In the following, we will use the discrete mode approximation for the expansion of the matter–wave functionΨ(x).Firstly, because of the interaction of the matter field with the optical field, the atoms are excited from the ground state of the condensate into states with momentap=±2ˉhk,±4ˉhk,...which means that each of them may form a number of quasimomenta, wherekis the wave vector of the cavity photons.Furthermore, in the simplest case, it is considered that the weakly interacting regime,U0〈?c??c〉 ≤10ωr(ωr= ˉhk2/2mais the recoil frequency of the condensate atoms). Then only the first two symmetric momentum side modes with moment±2ˉhkwere excited by fluctuations as a result of the atom–light interaction. Considering the parity conservation and the Bogoliubov approximation, the atomic field operator can be expanded as follows:[50]


whereγcandγmare the decay rates of atoms and the mechanical resonator, respectively. For simplicity, using the mean field assumption〈c?c〉=〈c?〉〈c〉,〈Xc〉=〈X〉〈c〉, and〈Qc〉=〈Q〉〈c〉, and ignoring some small quantum correlations but without loss of generality. In the weak laser driving regime,especially in the strong coupling region of a single photon,the nonlinear interaction between the cavity field and atomic Bogoliubov mode and the mechanical mode affect the response of the system to the probe field. Next,using the perturbation method to deal with Eqs.(5)–(9). The total solution of cavity and atomic Bogoliubov mode and the mechanical mode can be written as〈c〉=c0+δc,〈X〉=X0+δX, and〈q〉=q0+δq. The steady-state solution of Eqs. (5)–(9) can be obtained as

whereΔ=Δc+ξX0-Gq0is the effective detuning,c0is the steady state amplitude of the cavity field,X0andq0are the new equilibrium position of the collective oscillation of the BEC and mechannical displacement for the static solution,respectively. Next, we consider the perturbation made by the probe field and ignore the high-order terms,the equations for the fluctuations can be obtained as

Under the second-order sideband approximation, the solutions of Eqs.(13)–(17)can be written as[14–19]

The physical picture of Eq.(18)is that when the control field and the probe field incident into the cavity, due to the nonlinear interaction termsδcδX,δcδq, andδcδc*, a series of frequencies output fieldsωpr±nδare generated, wherenis an integer representing the sideband order. In Eq. (18) the parametersc-1andc+1are the coefficients of the first upper sideband (the anti-Stokes field with frequencyωpr+δ) and lower sideband(the Stokes field with frequencyωpr-δ).Similarly,c-2andc+2in Eq.(18)are the coefficients of the second upper (with frequencyωpr+2δ) and lower sidebands (with frequencyωpr-2δ). It is well known that the coefficient of the SS is much smaller than that of the first-order sideband. We only consider first-order and SS and ignore the HS effect.[14–19]
And then we use the following input–output relation:

3. Results and discussion
In order to explicitly illustrate the properties of the transmission intensity of the probe field and the dimensionless amplitudes of the SS in the hybrid COMS, the realistic parameters of our system are selected as follows.[49,50]ConsideringN= 2.3×10487Rb atoms inside a single-mode cavity with lengthL=1.78×10-4m,which is driven by the external field with wavelengthλp=780 nm and with decay rateκ= 2π×1.3 kHz. Further, the recoil of atomic mode isωr=2π×3.8 kHz with damping rateγc=0.001κ. The moving end mirror with frequencyωm=1.1Ωcand damping rateγm=0.001κ. We are based on the following two conditions:one is known as the resolved sideband conditionωm?κ, to ensure that we can distinguish the normal mode splitting. The second one is that the cavity is driven by the red-detuned cavity fieldΔ=(ωm+Ωc)/2= ˉω.
Physically, when the coupling fieldωcis red detuned by an amount ˉωandωprapproach the cavity frequency in the three-mode COMS, the level scheme of the standard COMS is similar to that of a three-level medium as shown in Fig. 2.The|1〉?|3〉transition is the excitation at the weak probe laser, and the strong pump laser is red detuned by an amountˉω= (ωm+Ωc)/2 to induce OMIT. Due to radiation pressure, additional coherence is created between the mechanical modes, resulting in OMIT splitting. From Fig. 2, the destructive interference has two paths when the two resonant frequencies are different, which means that the probe field has two OMIT Windows. Because of the radiation pressure,OMIT is analogous to driving hyperfine transitions in a Λ-type three-level atomic system via a radio-frequency or microwave field.[42]
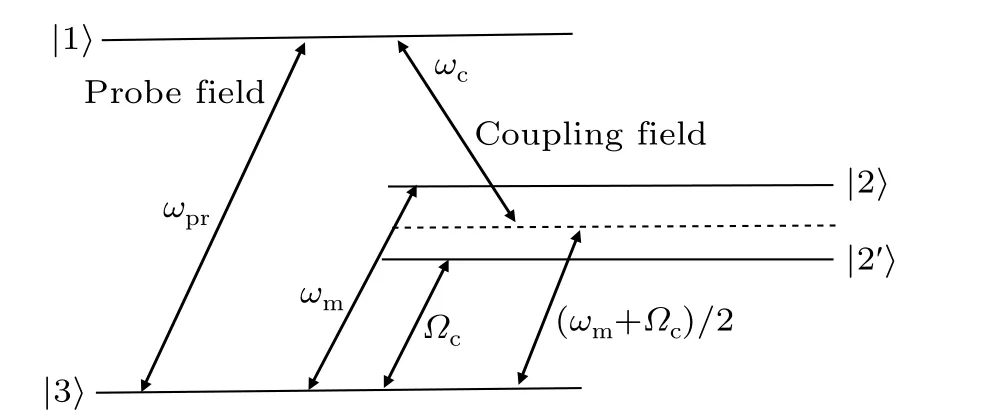
Fig. 2. The level diagram of the optomechanical system. The |1〉?|3〉transition is the excitation at the cavity frequency, the coupling laser is red detuned by an amount ˉω =(ωm+Ωc)/2 to induce OMIT.
Next,we focus on the features of the transmission intensity and the dimensionless amplitude of the SS in this hybrid COMS based on the analytical expressions in Eqs. (25) and(26).In order to modulate the hybrid COMS,we will study the dependence of the transmission intensity and the dimensionless amplitude of the SS on the COMS parameters,including the control field intensity, the nonlinear atom–atom interaction,the effective detuning,the effective coupling strength of the cavity field with the Bogoliubov mode.
Firstly, the transmission intensity|tp|2of the probe field and the dimensionless amplitudeηsof the SS are plotted as a function of the probe–pump detuningδ/ˉωfor different the control field intensities: (i)Epu=0.075ωm,(ii)Epu=0.1ωm,(iii)Epu=0.4ωmin Fig. 3. As clearly seen from Figs. 3(a)and 3(d), figure 3(a) shows that there is only one transparent window at theω= ˉω-ω0, that means the probe field is almost completely absorbed in another transparent window atω= ˉω+ω0. From Fig. 3(d), the dimensionless amplitude of the SS exhibits two normal dips atω= ˉω+ω0andω= ˉω-ω0, hereω0is the small deviation from the central frequency ˉω. Figures 3(b) and 3(e) show the dimensionless transmission intensity|tp|2and the dimensionless amplitudeηsof the SS vary withδ/ˉωunder a stronger control fieldEpu=0.1ωm. Figure 3(b)shows that there are two transparent windows atω= ˉω±ω0, which, however, are not very deep.Figure 3(e) shows the dimensionless amplitudeηsof the SS under the same control field,one can see thatηsalso becomes obvious near exhibit two normal dips at theω= ˉω±ω0. Figures 3(c)and 3(f)show the transmission intensity|tp|2and the dimensionless amplitudeηsof the SS vary withδ/ˉωunder much stronger control fieldEpu=0.4ωm. On the one hand,the transmission intensity|tp|2and the dimensionless amplitudeηsof the SS exhibit two normal dips at theω= ˉω±ω0.On the other hand,one obvious phenomenon is that the SS also shows two windows,and the windows become more and more obvious with the increase of the intensity of the control field.The physical effects can be explained by the radiation pressure coupling of cavity modes. OMIT relies on quantum interference,the coupling between the cavity field and the Bogoliubov mode and the mirror breaks the symmetry of the OMIT interference,then a single OMIT window is split into two.
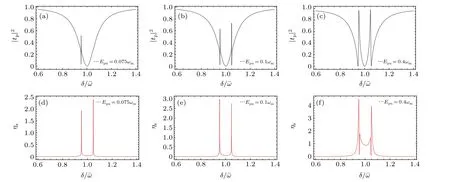
Fig.3. Calculation results of the transmission intensity|tp|2 and the dimensionless amplitude of the second-order sideband ηs vary with δ/ˉω for different control field intensities: in panels (a) and (d), we use Epu =0.075ωm; in panels (b) and (e), we use Epu =0.1ωm; and in panels (c) and (f), we use Epu=0.4ωm. The other parameters are g0=2π×10.9 MHz,N=2.3×104,Ωc=2π×15.2 kHz,ωm=1.1Ωc,Δa=2π×32 GHz,κ =2π×1.3 kHz,and γc=γm=0.001κ.

Fig.4. Calculation results of the transmission intensity|tp|2 and the dimensionless amplitude of the second-order sideband ηs vary with δ/ˉω for different control field intensities: Epu=0.1ωm (black line),Epu=0.3ωm (red dash line),Epu=0.8ωm (yellow line),meanwhile,calculated for different atom–atom interactions: in panels (a) and (d), we use ωsm =0; in panels (b) and (e), we use ωsm =0.5ωr; and in panels (c) and (f), we use ωsm =ωr. The other parameters are the same as those in Fig.3.
Secondly,in order to observe the effect of atom–atom interaction on the transmission intensity|tp|2and the dimensionless amplitudeηsof the SS,we have plotted|tp|2andηsof the system whether in the absence of BEC or in the presence of BEC in Fig. 4. There are three different interaction values:ωsm=0 (Figs. 4(a) and 4(d)),ωsm=0.5ωr(Figs. 4(b) and 4(e)),andωsm=ωr(Figs.4(c)and 4(f)). Meanwhile,we have plotted the transmission intensity|tp|2and the efficiency amplitudeηsof the SS, versus the normalized cavity-pump detuningδ/ˉωfor different control field intensities:Epu=0.1ωm(black line),Epu=0.3ωm(red dash line),Epu=0.8ωm(yellow line).


The effective frequency detuning is an important parameter for modulating the hybrid COMS.So we show the transmission intensity|tp|2(see Figs.5(a)–5(c))and the dimensionless amplitudeηsof the SS(see Figs.5(d)–5(f))varying with probe–pump detuningδ/ˉωand the effective atom–pump detuningΔ/ˉωfor three different atom–atom interaction values:ωsm=0.5ωr(Figs. 5(a) and 5(d)),ωsm=ωr(Figs. 5(b) and 5(e)),andωsm=1.5ωr(Figs.5(c)and 5(f)). We can find that|tp|2andηssensitively depend on the effective atom–pump detuningΔ. With the atom–atom interaction strength increasing,the local maximums of|tp|2andηshave greatly enhanced at the non-resonant position of the probe–pump detuning. In fact,the detuning regulation of nonlinear response plays a very important role in optical nonlinear modulation. The effective frequency detuning between the cavity field and the control field can change the transmission intensity and affect the dimensionless amplitude of the SS output. Comparison of|tp|2in Figs.5(a)–5(c)withηsin Figs.5(d)–5(f),the maximums of|tp|2andηsare always located in the very narrow frequency range for a fixed probe–pump detuning,and their corresponding transmission intensity|tp|2andηspresent an asymmetric dip,as shown in Fig.4.

Fig.5.Contour maps of the transmission intensity|tp|2 including[(a)–(c)]and the dimensionless amplitude of the second-order sideband ηs including[(d)–(f)]as a function of the effective atom–pump detuning Δ/ˉω and the control field detuning δ/ˉω with different atom–atom interaction strengths: ωsm =0.5ωr in panels(a)and(d),ωsm=ωr in panels(b)and(e),and ωsm=1.5ωr in panels(c)and(f). The other parameters are the same as those in Fig.3.
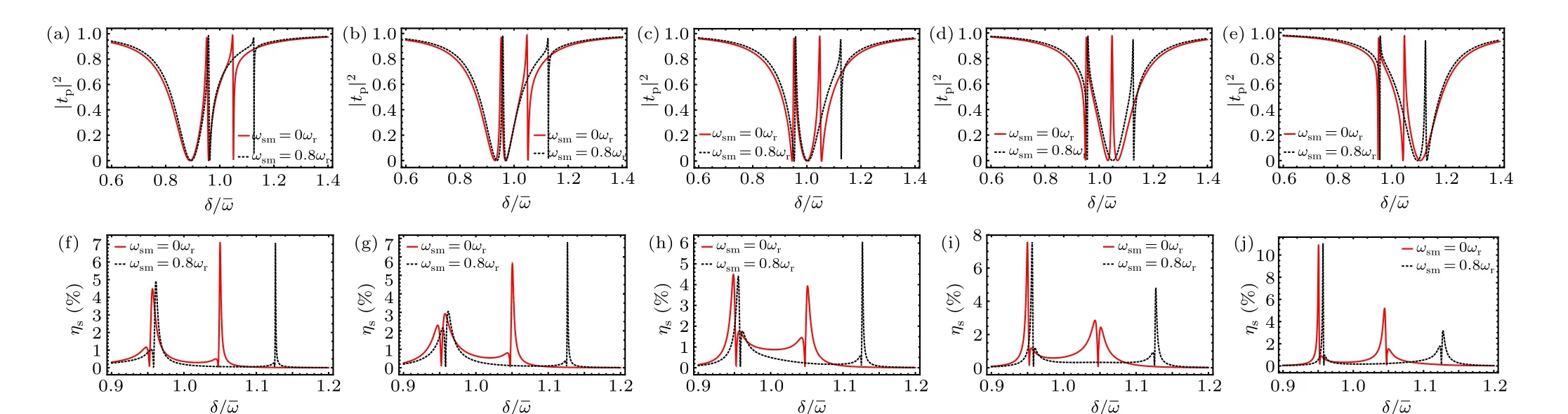
Fig. 6. Calculation results of the transmission intensity |tp|2 and the dimensionless amplitude of the second-order sideband ηs vary with δ/ˉω for different atom–pump detunings: Δ =0.9ˉω,Δ =0.95ˉω,Δ = ˉω,Δ =1.05ˉω,and Δ =1.1ˉω. The red line for ωsm =0 and the black dash line for ωsm =0.8ωr. The other parameters are the same as those in Fig.3.

Fig. 7. Calculation results of the transmission intensity |tp|2 and the dimensionless amplitude of the second order sideband ηs vary with δ/ˉω for different effect coupling strengths: ξ =0.5ξ0,ξ =ξ0,ξ =3ξ0. The other parameters are the same as those in Fig.3.
The results also confirm that the effective frequency detuning of the control field is a very significant parameter,which enables us to change the transmission intensity|tp|2and improve the dimensionless amplitudeηsof the SS.In order to see the effective atom–pump detuningΔon the transmission intensity|tp|2and the dimensionless amplitudeηs,we plot|tp|2andηsas a function of the probe–pump detuningδ/ˉωfor different atom–pump detunings:Δ=0.9ˉω,Δ=0.95ˉω,Δ= ˉω,Δ=1.05ˉω,andΔ=1.1ˉωin Fig.6. We can see clearly from the figure, the transmission intensity|tp|2of the probe field and the dimensionless amplitudeηsof the SS generation can be modulated efficiently by adjusting the effective detuningΔ.Comparing|tp|2in Figs. 6(a)–6(e) withηsin Figs. 6(f)–6(j),when the effective atom–pump detuningΔ= ˉω, the transmission intensity|tp|2of the probe field and the dimensionless amplitudeηsof the SS generation presents symmetrical profile with two splitting peaks. However, whenΔ=0.9ˉω,Δ= 0.95ˉωis tuned to less than ˉω, or whenΔ= 1.05ˉω,Δ=1.1ˉωis tuned to more than ˉωon the atom–atom interaction strengthωsm=0,on the one hand,a very obvious phenomenon is that symmetrical transparency windows become asymmetrical;on the other hand,whenΔ <ˉω,the right peak of the effective amplitudeηsprofile is enhanced remarkably which can see Figs.6(f)and 6(g),whileΔ >ˉω,the left peak of the effective amplitudeηsprofile is amplified significantly which can see Figs.6(i)and 6(j). However,even the effective atom–pump detuningΔ= ˉω,when the atom–atom interaction strengthωsm=0.8ωr, comparing the red line with the black dash line in Figs.6(c)and 6(h),there are two pronounced phenomena,one is that the symmetry of the profile is broken,another one is that the right peak is away from the center. In addition, when the effective atom–pump detuningΔ/=ˉω, the phenomenon is the same as that without the atom–atom interaction strength. It is well known that the exchange between phonons and photons can be effectively controlled by modulating efficient atom–pump detuningΔ. Thus, the density of the photons in the cavity and the photon pressure on the mechanical resonator can also be tuned to each other by effective atom–pump detuningΔ. So the transmission intensity|tp|2and the dimensionless amplitudeηsof the SS generation will be adjusted significantly.
Finally, the transmission intensity|tp|2and the dimensionless amplitudeηsare plotted as the probe–pump detuningδ/ˉωfor the effect coupling strengths:ξ=0.5ξ0,ξ=ξ0,ξ=3ξ0in Fig.7. With the increase of effect couplingξbetween Bogoliubov and optical mode, not only the SS effect can be produced,but also the left peak value increases significantly. The stronger of the effective coupling strength is,the higher of the peak will get. It can be seen that the stronger SS effect can achieve in such kind of a hybrid COMS.By controlling the coupling intensity between Bogoliubov and the optical mode, the generation efficiency of the SS can improve obvious.
4. Conclusion
In conclusion,we theoretically and numerically analyzed the nonlinear optical transmission characteristics of a hybrid COMS in which a BEC is trapped inside an optical cavity with a moving end mirror. First of all, we obtained the analytical expressions of the transmission intensity|tp|2and the dimensionless amplitudeηsof the SS. The tunable SS effects can be obtained by using the atom–atom two-body interaction as a new handle. It is one of the most exciting features of such hybrid COMS containing the BEC,we can obtain the controllability of the frequency of the Bogoliubov mode which can be altered by using the s-wave scattering interaction. Moreover, it has been shown that numerical results show that the transmission intensity|tp|2and the dimensionless amplitudeηsof the SS can be adjusted by the COMS parameters,including the control field intensities,the effective detuning,and the effective coupling strength.
To demonstrate that the transmission intensity|tp|2and the dimensionless amplitudeηsof the SS investigated here are within the experimental reach, we discussed the experimental parameters from Refs. [49,50], a BEC of typicallyN=2.3×10487Rb atoms is coupled to the light field of an optical ultra-high finesse Fabry–P′erot cavity. The atom–field couplingg0=2π×10.9 MHz and typically atom–pump detuning isΔa=2π×32 GHz. We choose a particular set of parameters and procedures very close to the present experimental ventures,which makes our study experimentally feasible. We believe that this new method of generation of the SS proposed in this paper will implemente by the present experiments shortly.
Appendix A:Derivation of SS analytical expressions
Here we provide some details about the SS analytical expressions. We substitute Eqs. (16)–(20) into Eqs. (11)–(15),and compare the coefficients in the same order. After some calculations, we can obtain the first-order sideband equations as follows:


Acknowledgments
Project supported by the National Natural Science Foundation of China (Grant Nos. 11564034 and 21663026), the Natural Science Foundation of Gansu Province,China(Grant No. 20JR5RA509), the Fundamental Research Funds for the Central Universities of College of Electrical Engineering, Northwest Minzu University (Grant Nos. 31920210016,31920190006,and 31920200006),and the Scientific Research Project of Hunan Educational Department, China (Grant No.19B206).
- Chinese Physics B的其它文章
- Design of vertical diamond Schottky barrier diode with junction terminal extension structure by using the n-Ga2O3/p-diamond heterojunction
- Multiple modes of perpendicular magnetization switching scheme in single spin–orbit torque device
- Evolution of the high-field-side radiation belts during the neon seeding plasma discharge in EAST tokamak
- Phase-matched second-harmonic generation in hybrid polymer-LN waveguides
- Circular dichroism spectra of α-lactose molecular measured by terahertz time-domain spectroscopy
- Recombination-induced voltage-dependent photocurrent collection loss in CdTe thin film solar cell

