Kondo screening cloud in a superconductor with mixed s-wave and p-wave pairing states

Zhen-Zhen Huang(黃真真), Xiong-Tao Peng(彭雄濤), Wan-Sheng Wang(王萬勝), and Jin-Hua Sun(孫金華)

School of Physical Science and Technology,Ningbo University,Ningbo 315211,China

Keywords: Kondo effect,Rashba spin–orbit couplings,p-wave superconductors,Anderson model

1. Introduction

The Kondo effect arises when local magnetic impurity spins couple antiferromagnetically with conduction electron spins. As a prototypical strong correlation problem,Kondo effect in normal metals has been widely studied and well understood.[1,2]If the temperature is above the so-called Kondo temperatureTK,the magnetic impurities can be treated perturbatively. However, at temperatures well belowTK, perturbation theory fails, and it has been confirmed, using the numerical renormalization group study,that the magnetic impurity spins are entirely screened by the conduction electron spins.[3]

When the magnetic impurity couples to an s-wave superconductor,the low-energy transport is dominated by the spininduced Yu–Shiba–Rusinov (YSR) state,[4–6]which is determined by the competition between the Kondo effect and the superconductivity. The ground state will be a Kondo singlet ifTK＞Δ,otherwise the ground state will be a magnetic doublet ifTK＜Δ, whereΔis the superconducting gap. The interest in magnetic doping in superconductors persists because it can provide information to understanding the properties of superconducting states. The properties of YSR states is one of the major methods to characterize the pairing symmetry of the superconducting states,and has been widely studied in the high-temperature cuprate superconductors,[7–10]iron-based superconductors,[11–13]chiral p-wave superconductors,[14,15]topological superconductors,[16,17]nematic superconductors,[18]etc. More recently, the pairing symmetry dependent YSR states are studied in the superconducting phase of twisted bilayer graphene.[19]

Besides the YSR states, the formation of the Kondo screening cloud, which is characterized by the spin–spin correlation function between the magnetic impurity and the conduction electrons, is also a fascinating problem. In aDdimensional normal metal, the spin–spin correlation function follows a power law decay 1/rDifr ＜ξK, but 1/rD+1ifr ＞ξK, withξKbeing the Kondo coherence length.[20–22]Numerical renormalization group study shows that in an swave superconductor, the Kondo screening cloud is formed in both the screened and unscreened phases, and decays with respect to 1/rin the vicinity of the magnetic impurity, and the decay rate in larger distances depends on the magnitude of the superconducting gap.[23]Note that the signatures of the Kondo screening cloud extending over a length of micrometers has been confirmed recently via Fabry–P′erot oscillations in conductance.[24]

In unconventional superconductors, the magnetic impurity behavior is more complicated. Numerical renormalization group study shows that despite sharing the p+ip pairing symmetry,intrinsic and extrinsic topological superconductors host different physical processes that produce distinct Kondo signatures.[25]The magnetic doping in the intrinsic p-wave pairing states corresponds to a strong spin doublet ground state with partially screened magnetic impurity spin. In the extrinsic p-wave pairing states, the Kondo screening involves both the electron and orbital degrees of freedom to produce rich and prominent Kondo phenomena. In the presence of Rashba spin–orbit coupling(RSOC),the YSR state exhibits Zeemandependent splitting behaviors.[26]

The purpose of this paper is to investigate the properties of the binding energy and the spatial Kondo screening cloud in a superconductor with coexisting s-wave and p-wave pairing states. The variational method we apply has been used to study the ground state of the Kondo problem in normal metals,[27,28]antiferromagnet,[29]2D helical metals,[30]various 3D topological semimetals.[31–35]It has also been applied to study the magnetic impurity effects in the s-wave and dwave superconductors.[36–39]Due to the combined effects of the RSOC and the Zeeman field,the Kondo screening cloud is expected to show very interesting features,such as the spatial anisotropy and the emergence of the off-diagonal components of the spin–spin correlation function.

The paper is organized as follows. We introduce the Anderson model Hamiltonian in Section 2.In Section 3,we apply the variational method to study the binding energy. In Section 4, we investigate the spin–spin correlation between the magnetic impurity and the conduction electrons in the superconductor with coexisting s-wave and p-wave pairing states.Finally,the discussions and conclusions are given in Section 5.

2. Anderson model Hamiltonian

The mixed s-wave and p-wave pairing states can be generated in a heterostructure fabricated by a combination of an s-wave superconductor and the two-dimensional electron gas (2DEG) with RSOC.[40–42]The Zeeman field induced by the ferromagnetic insulator can significantly alter the superconducting states, and even lead to a topological phase transition.[43,44]

We use the well-known Anderson impurity model to study the Kondo screening of a spin-1/2 magnetic impurity coupled to the mixed s-wave and p-wave pairing states. The Anderson model Hamiltonian reads

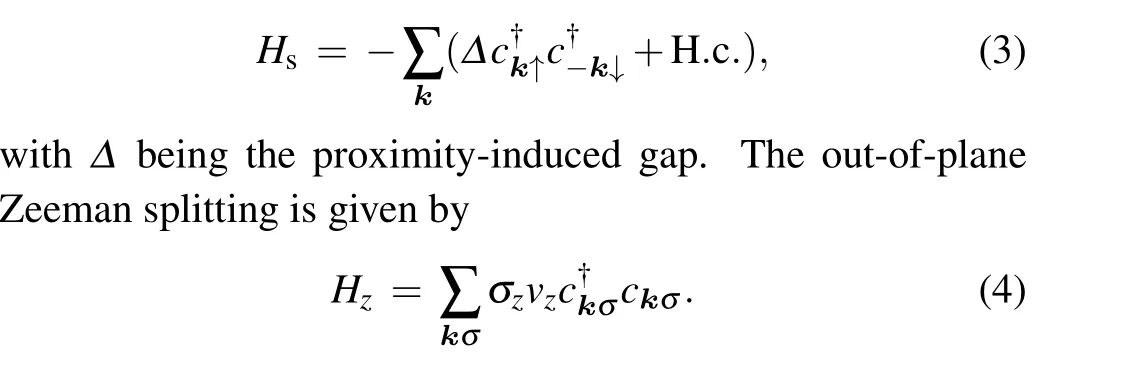
σzis thez-component of the spin Pauli matrix. The p-wave pairings can be induced in the 2DEG with the aids of RSOC and s-wave pairing states.[40–42]In fact,the Zeeman field shall couple both to the spins of the bulk electrons and to the delectrons,depending on thegfactors which need not be equal for the two cases. It is well-known that the spin degeneracy of the impurity energy level shall be lifted by the Zeeman field,leading to a Kondo peak splitting. However, to eliminate the additional complexity caused by the Zeeman splitting of the impurity energy level and mainly concentrate on the interplay between the Kondo effect and the mixed s-and p-wave pairing states,we assume that thegfactor for the magnetic impurity is zero. This case has been discussed before[26,45,46]and seems to be achievable in quantum dots.[47]The Hamiltonian of the magnetic impurity is

whereVis the hybridization strength. For simplicity, we set the position of the impurity as the originr=0, so that the hybridizationVis in fact independent of spin and momentum.

To deal with the RSOC term and the superconducting pairings,we switch to a continuum representation

3. The self-consistent calculation

To investigate the eigenstate property, we utilize a trial wavefunction approach.The Coulomb repulsionUis assumed to be large enough, andεdis below the Fermi energy, so that the impurity site is always singly occupied by a local moment.When a magnetic impurity is coupled to an s-wave superconductor,the ground state will be a Kondo singlet ifTK＞Δ,otherwise the ground state will be a magnetic doublet ifTK＜Δ,whereΔis the superconducting gap. The ground state is determined by the competition betweenTKandΔ. However,quite distinctly,magnetic impurities in an intrinsic p-wave superconductor always form a magnetic doublet ground state.When the s-and p-wave pairings coexist,the ground state becomes very interesting, and a quantum phase transition from a magnetic doublet to a singlet ground state takes place as the RSOC increases.[26]In our calculations,we consider very large RSOC(λ)and hybridization strength(V)in comparison to the superconducting gap, and assume that the ground state is a Kondo singlet. The trial wavefunction is given by[36–39]

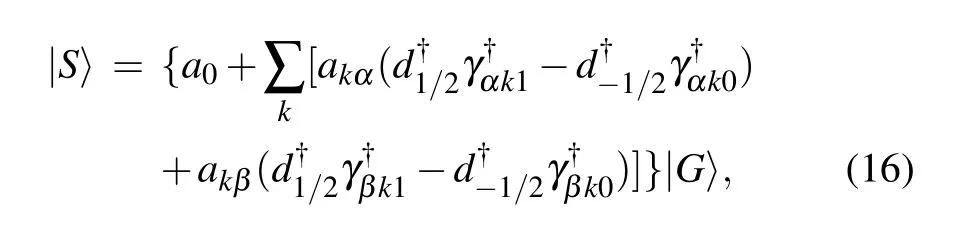
wherea0,akα,akβare the variational parameters to be determined through self-consistent calculations.|G〉is the ground state of the superconductor, andγαki|G〉=γβki|G〉=0 (i=0,1). In fact,virtual excitations to the doubly occupied intermediate state can affect the spin exchange process in the Anderson model. Using the Schrieffer–Wolff transformation and to the lowest order of hybridizationV,the Anderson model in thend=1 subspace turns to be equivalent to the s–d exchange model with the effective couplings containing both the doubly occupied intermediate state and the singly occupied states.However, in strong repulsion limit,U →∞, the contribution of the doubly occupied intermediate state becomes negligible.Hence in the trial wavefuncion, we assume a singlet ground state with two terms: the first term describes the amplitude for the filled Fermi sea with an empty impurity site, and the second term with the summation overkdescribes the superposition of states with a singly occupied impurity level.

The energyESof the total Hamiltonian in the singlet state|S〉is

In all our calculations,Δ0=W/2500 indicates a typical superconducting gap size,andWis the bandwidth far from the Fermi surface, such that the energy cutoff has minor impact on the low-energy physics. The chemical potential is fixed asμ=0, and the impurity energy level is slightly below the Fermi surface thatεd-μ=-Δ0/20.

In Fig.1 we show the self-consistent results of the binding energy of a superconductor with mixed s-wave and p-wave pairing states. The results are obtained by numerically solving Eq. (22). In Fig. 1(a) we show the self-consistent results of the binding energyΔbwith respect to hybridizationVforΔ=Δ0for various combinations of parametersλandvz. We can see that with the increase ofλ,the binding energyΔbalso increases, indicating that Kondo singlet is favored for large RSOC. The Kondo screening of a magnetic impurity in an otherwise clean 2DEG with RSOC has been studied in previous works using various methods, and it was shown that in general,the RSOC has weak influence on the Kondo temperature. The Kondo temperature displays a quasilinear dependence on the square of the RSOC with a slope that is positive forεd+U/2＞0, and negative forεd+U/2＜0.[46,48,49,55]There also exists another scenario for an isolated system with a constant band filling and a Fermi energy that varies with the RSOC,once the RSOC exceeds a critical value proportional to bottom of the bands in the absence of the RSOC, the system enters the helical metal regime andTKrises rapidly.[46]However,the binding energyΔbdecreases for larger Zeeman fieldvz. In general, for all the cases,Δbincreases monotonically with respect toV, indicating that the Kondo singlet states are more easily formed with larger hybridizations. This behavior is in general consistent with the results given in the s-wave superconductor. The formation of the ground state is determined by the competition between the Kondo temperatureTKand the superconducting gapΔ,and largerTKcorresponds to largerV.If the hybridization is strong enough, the ground state is always a Kondo singlet, while weak hybridization corresponds to the magnetic doublet ground state where the impurity remains partially screened. Figure 1(b)is the self-consistent results of the binding energyΔbwith respect to superconducting gapΔforV=27.5Δ0. As we can see,Δbgrows monotonically withλ,but decreases ifvzbecomes larger. Furthermore,the binding energyΔbreduces as the superconducting gapΔincreases, indicating that the larger the superconducting gap is, the more difficult it is for the impurity electrons to break the superconducting pair and form a Kondo singlet.

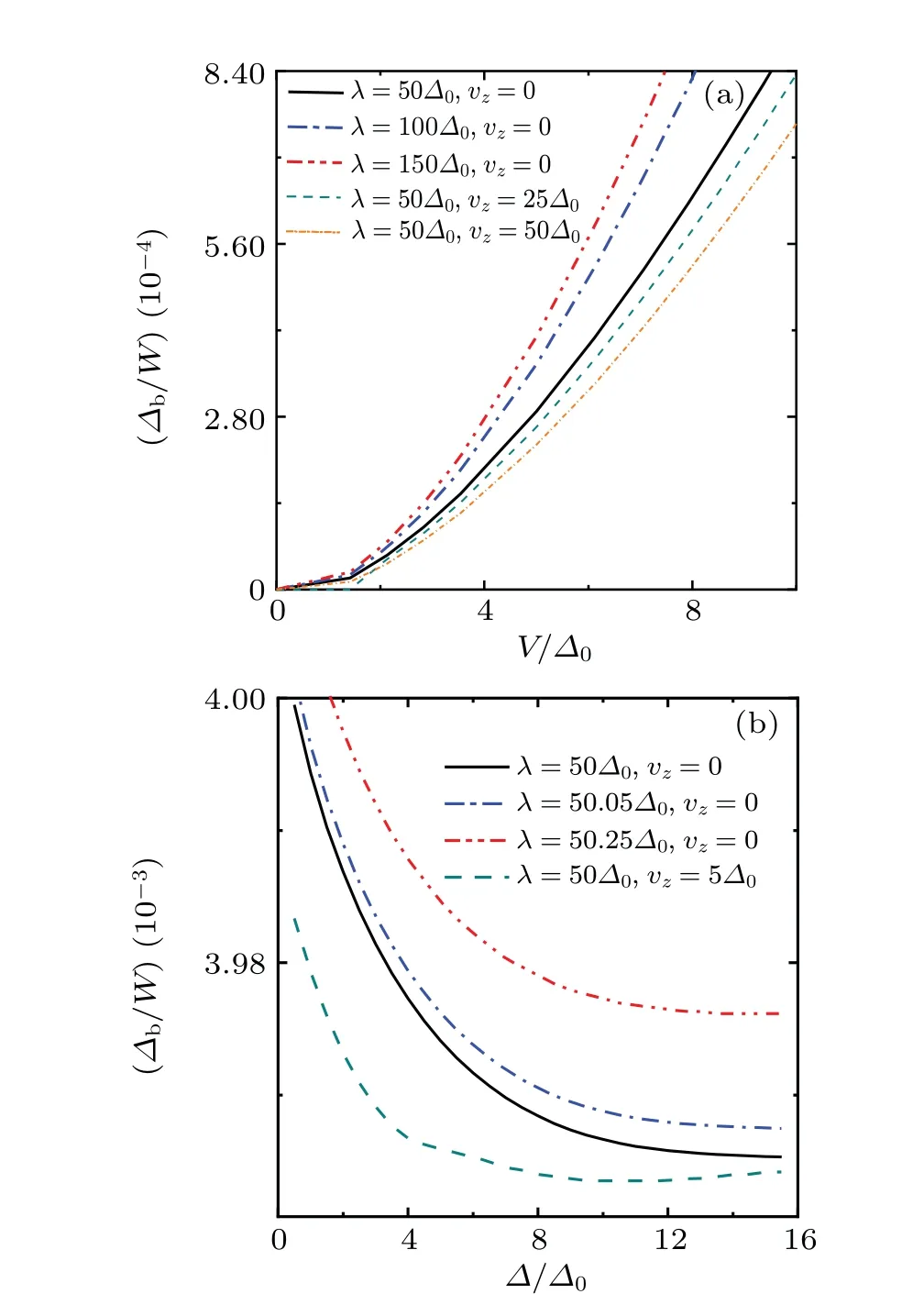
Fig.1. Self-consistent results of the binding energy Δb(a)with respect to hybridization V for Δ =Δ0 and(b)with respect to superconducting gap Δ for V =27.5Δ0. The results are given for various combinations of parameters λ, vz, Δ. In all the calculations, Δ0 =W/2500 indicates a typical superconducting gap size, and the bandwidth and chemical potential are fixed at W =2500Δ0 ?Δ0 and μ =0.

4. The spin–spin correlation

wheremandnare the orbital angular momentum quantum number,φis the polar angle of spatial coordinater, that is,φ= arctan(ry/rx). The parametersCii′(r,m,n) (i,i′=1,2,3,4) are defined in Appendix B. Ifvz=0, it is easy to obtainβ1k=β-1k, and thenC12(r,m,n)=C13(r,m,n) such thatJxy(r)=Jyx(r). In all the results of spin–spin correlation function we present below,the binding energy is fixed asΔb=5Δ0. Actually the magnitude of the binding energy depends on various parameters of the Hamiltonian. However,the spatial patterns of the spin–spin correlation function are not much affected by the values ofΔbexcept the magnitudes.

In Fig.2 we show the diagonal and off-diagonal terms of the spin–spin correlation between the magnetic impurity and the conduction electrons in the coordinate space. Here we fixV= 27.5Δ0,λ= 50Δ0,Δ=Δ0, andvz= 0, andkcis the momentum cutoff chosen with respect to the energy cutoffW.One can see thatJxx(r)andJyy(r)are anisotropic,whileJzz(r)is isotropic for the diagonal term. In addition,Jyy(r) can be obtained by rotatingπ/2 byJxx(r). For off-diagonal terms,Jyx(r)=Jxy(r),Jzx(r)=-Jxz(r),andJzy(r)=-Jyz(r),andJxz(r) can be obtained with rotatingπ/2 angle byJyz(r).These results agree well with those of our symmetry analysis.

In Fig. 3 we show the decay ofJzz(r) along thex-axis with different parameters ofλ,Δ0andvzforV= 27.5Δ0.Jzz(r)is rotational symmetric in thex–yplane. Whenvz=0,Jyy(r)=Jzz(r)along thex-axis andJxx(r)=Jzz(r)along they-axis. One can see thatJzz(r)decays faster with the increase ofλ, energy gapΔand magnetic fieldvz. Numerical renormalization group study shows that in an s-wave superconductor,the Kondo screening cloud is formed in both the screened and unscreened phases, and decays with respect to 1/rin the vicinity of the magnetic impurity,and the decay rate in larger distances depends on the magnitude of the superconducting gap.[23]

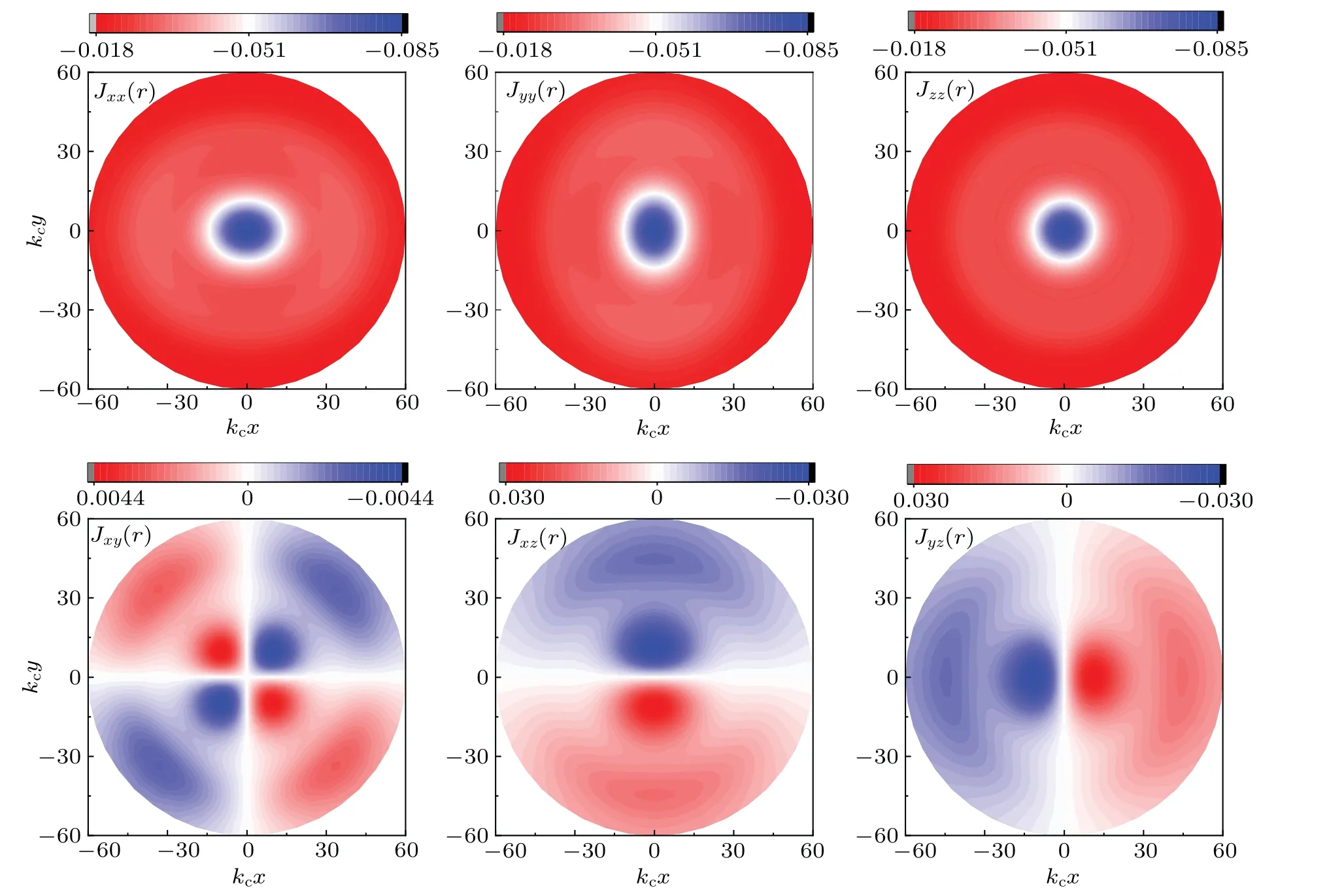
Fig.2. Terms of the spin–spin correlation Juν(r)(u,ν=x,y,z)in coordinate space for V =27.5Δ0,λ =50Δ0,Δ =Δ0,and vz=0,where kc is the momentum cutoff chosen with respect to the energy cutoff W. The off-diagonal terms not shown here have the relations Jyx(r)=Jxy(r),Jzx(r)=-Jxz(r),and Jzy(r)=-Jyz(r).

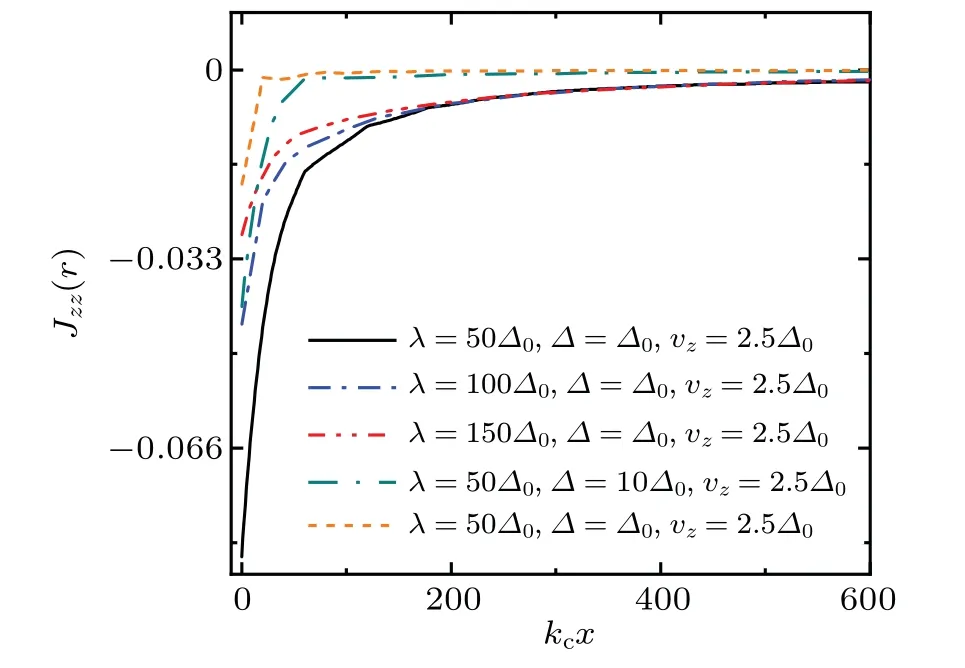
Fig.3. Spatial decay behavior of Jzz(r)along the x-axis with different parameters of λ,Δ0 and vz for V =27.5Δ0.

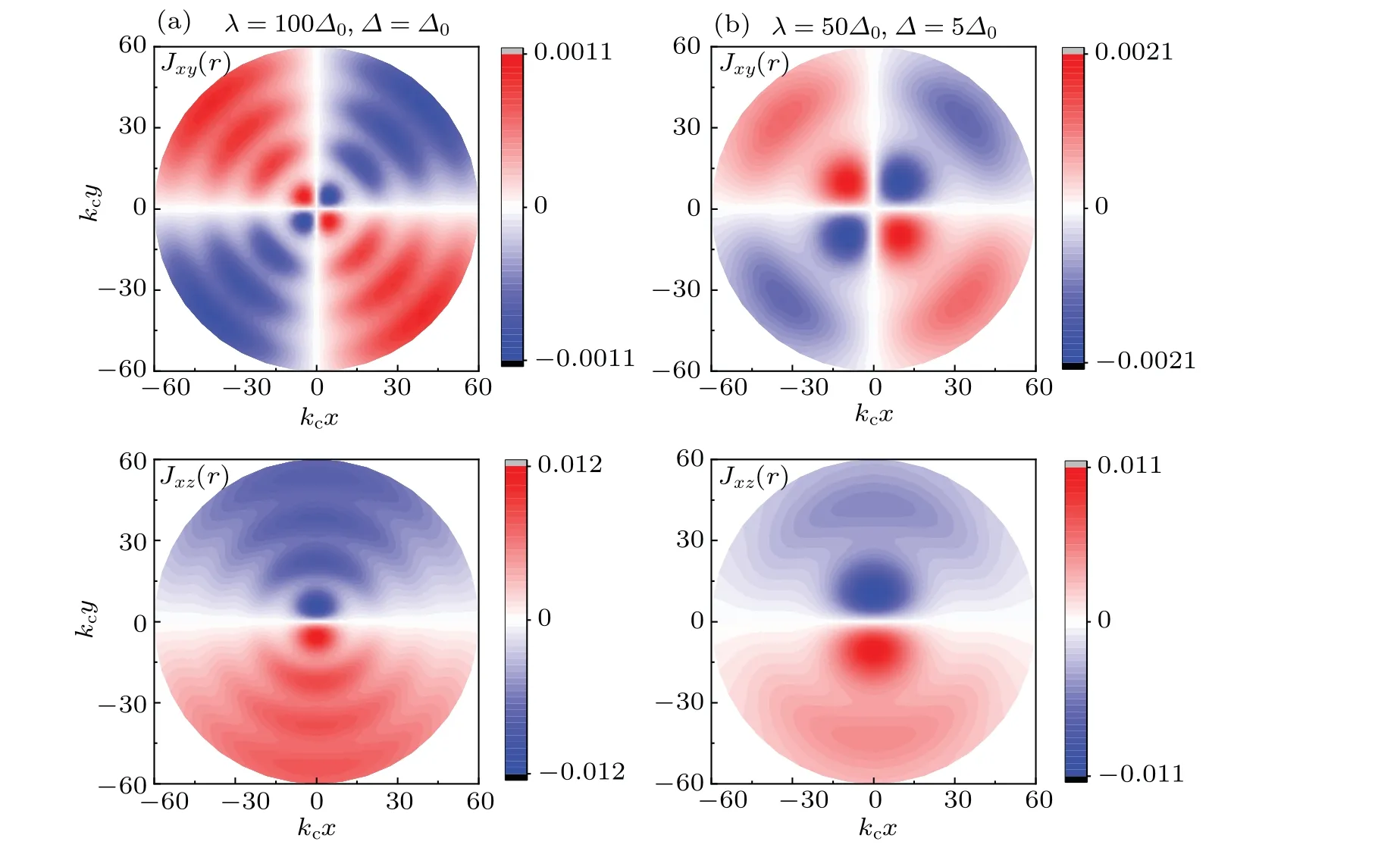
Fig.4. Off-diagonal terms of spin–spin correlation for(a)λ =100Δ0,Δ =Δ0(the left column)and(b)λ =50Δ0,Δ =5Δ0(the right column).The hybridization is V =27.5Δ0,and Zeeman field is vz=0. Jyz(r)=Jxz(?z(π/2)r),so it is not shown here.

Fig.5. The change of Juν(r)when vz/=0,with λ =50Δ0,Δ =Δ0,V =27.5Δ0. The Zeeman field is(a)vz=2.5Δ0 and(b)vz=50Δ0.

5. Discussion and conclusion

In summary, we have utilized the variational wavefunction method to study the binding energy and the spatial anisotropy of the Kondo screening cloud in a superconductor with coexisting s-wave and p-wave pairing states. The host system is constructed from a combination of an s-wave superconductor, a ferromagnet which produces a Zeeman field,and a semiconductor with RSOC.The ground state of a magnetic impurity in a conventional s-wave superconductor or a intrinsic p-wave is a well-studied problem.When the two pairings are mixed, the Kondo screenings show interesting features. We concentrate on the binding energy and the spin–spin correlation function which describes the so-called Kondo screening cloud, and systematically study the effects of the RSOC, Zeeman field, and superconducting gap size on the Kondo screening. From the results of the binding energy calculations, we find that Kondo screening is favored for strong RSOC and weak Zeeman field cases. In general, the binding energy grows monotonically with the hybridization strength,and decreases when the superconducting gap increases,which is in consistence with the picture that the ground state is determined by the competition betweenTKandΔ. Due to the RSOC,the diagonal components become anisotropic,and various off-diagonal components emerge. The spin–spin correlation decays fast in the real space,and Zeeman field induces extra asymmetry to the off-diagonal components. So far, we assume a singlet ground state,which is reasonable ifV ?Δ.If we fix other parameters and gradually increaseV,the ground is expected to experience a transition from a magnetic doublet to a Kondo singlet. In the binding energy calculations, this transition can be detected by comparing the binding energy in the two ground states, and will be investigated in our future work.

Appendix A

By diagonalizing the Hamiltonian in Eq. (11), one can obtain the band structure

Appendix B

Acknowledgements

The computation is performed in the Supercomputer Center of Ningbo University.

Project supported by the Zhejiang Provincial Natural Science Foundation of China(Grant No.LY19A040003).