Finite-time synchronization of uncertain fractional-order multi-weighted complex networks with external disturbances via adaptive quantized control
Hongwei Zhang(張紅偉), Ran Cheng(程然), and Dawei Ding(丁大為)
School of Electronics and Information Engineering,Anhui University,Hefei 230601,China
Keywords: fractional-order complex networks, uncertain parameter, finite-time synchronization, quantized control
1. Introduction
In the last decade,as a new discipline of complexity science,complex networks(CNs)have attracted extensive attention and discussion in the academic field. The theories of CNs have been applied in biology,[1]social science,[2]computer science[3]and power system,[4,5]and some excellent achievements have been obtained. In real life,the connection among network nodes is often multi-weighted.[6,7]For example,in the information exchange between persons,in addition to the use of mobile phones to send messages, people also use e-mail,network chat software, and other party for information communication. It can be seen that the CNs with multi-weighted node connection have more practical significance and application value. However, at present, most of the studies only consider the dynamical behavior of CNs with a single weight and lack the in-depth study of multi-weighted CNs. Given the importance of this issue,some researchers have focused on it and achieved some results.[8–10]
Synchronization,as a crucial behavioral feature in the dynamic system, is a hot research field in CNs. In general, network synchronization refers to the process in which the states of all coupled dynamical systems tend to behave together over time.[11]Over the last several years,researchers have explored a variety of synchronization in CNs, such as complete synchronization,[12]projective synchronization,[13,14]quasi synchronization,[15,16]cluster synchronization,[17–19]and exponential synchronization.[20]In engineering applications,due to the requirements of security and efficiency,it is important to know the maximum synchronization time of the network.[21]Therefore, compared with the general synchronization mode without the upper limit of synchronization time,the finite-time synchronization is more meaningful and can be used in a wider range of scenarios.[22–25]In Ref. [23], Yinget al.articulated a new method to solve the problem of CNs synchronization within a limited time with Markovian switching topologies. In Ref.[24],Heet al.established a synchronization criterion for input delay CNs in limited time via non-fragile controller. In Ref. [25], Zhang researched the synchronization problem of CNs with disturbances in finite time when the node states are uncertain.
It is worth mentioning that in the above literature, some parameters of CNs are assumed to be known. But in practical applications, these parameters are often uncertain because of the constraints of some actual conditions. Furthermore, these parameters often have a significant effect on the whole network synchronization process.[26]Therefore, considering the synchronization of CNs with uncertain parameters has stronger practical significance.[27–29]In Ref. [27], Meiet al.investigated the identification and synchronization of finitetime structures in drive-response systems with uncertain parameters in finite time. In the case of delayed coupling networks, the Lyapunov stability theory has been used to obtain the outer synchronization criterion while the uncertain parameters were considered in Ref.[28].
Fractional calculus is an extension of calculus in the real number field. Compared to integer-order calculation, it takes into account the historical and non-local distributed influence. In other words,fractional calculus has the characteristics of memory and inheritance.[30,31]Because of this satisfactory property,fractional calculus can describe the physical model in practical applications more accurately,such as neural network[32,33]and chaotic memristor circuit.[34,35]Therefore,it is more valuable to consider the dynamic behavior of CNs under fractional-order perspective.[36–38]In Ref.[36],Liet al.studied the synchronization phenomenon of fractional order CNs using the method of graph theory and proposed a new finite-time synchronization theorem. In Ref. [37], the author accomplished finite-time synchronization and parameter identification of uncertain fractional-order CNs using fractional calculus principles and certain analytical approaches.
To make the network reach synchronization, many effective control methods have been proposed, such as pinning control,[39]intermittent control,[40]and event-triggered control.[41]However,there are few studies on quantitative control at present. As is well known, the signal transmission between network nodes depends on the transmission channel and channel bandwidth. Sometimes, due to the limitation of the channel itself,the signal in the transmission process results in the decline of the performance of the network.[42,43]Therefore, the quantification of the signal before transmission is an effective method to improve the transmission performance and enhance the stability of network communication.[44–46]In Ref. [44], authors considered the finite-time quantized synchronization for CNs with quantized time-varying delayed coupling. In Ref. [45], according to the use quantized output control method,the synchronization of the neural network with output coupling was realized.
Motivated by the aforementioned considerations, the issue of finite-time synchronization of FMCNs under adaptive quantization control is mainly studied. At the same time,uncertain parameters, coupling delay, and external interference are also taken into account, which makes the results of the study more practical. The main contributions of this paper are listed as follows:
(i) Different from Refs.[20,22,23],this paper not only considers the synchronization of CNs under the properties of fractional calculus,but also considers the influence of multiple weights on the synchronization of CNs, which is more practical.
(ii) Based on the logarithmic quantizer, this paper designs a new adaptive quantized controller, which enables the network to achieve synchronization in finite time,and the upper bound of synchronization time can be calculated.This paper also considers the finite-time synchronization problem of adaptive quantized control under no-coupling delay and coupling delay conditions, making the theory obtained in this paper more universal.
(iii) Uncertain parameters and external disturbances are taken into account simultaneously in the FMCNs studied in this paper. Under the conditions of coupling delay and no-coupling delay, through the logarithmic quantizer,we obtain parameter update laws and control methods,which can accurately identify the uncertain parameters of the system and eliminate the influence of external disturbances.
The remainder content is structured as follows. In Section 2,some necessary definitions and lemmas are given,and the FMCNs model is established.In Section 3,finite-time synchronization theorems for no-coupling delay and coupling delay are given, respectively. The correctness of the theorem is shown in Section 4 via illustrations of numerical simulation.Finally,the conclusion is given in Section 5.
Notions The rational set of real numbers is denoted by R, Rm×ndenotes the set of allm×nreal matrices, and Rmrepresents them-dimensional Euclidean space.‖·‖=(∑mp=1|x2p|)1/2denotes Euclidean norm.Imdenotes themorder identity matrix. For any matrixA,A >0 represent the matrixAis positive whileA <0 represents the matrixAis negative. Besides, theλmaxdenotes the maximun eigenvalue of the matrix.
2. Preliminaries
In this section, with the purpose of setting the problem preferably,some essential definitions of logarithmic quantizer and Caputo fractional calculus are reviewed, some helpful lemmas are presented,and the mathematical model of FMCNs is developed.
2.1. Logarithmic quantizer and Caputo fractional calculus
Definition 1[22]The logarithmic quantizerχ(τ):R→Π is built in the following way:


2.2. Model description
Consider FMCNs with time-delay coulped byMnodes,which would be summarized by the following mathematical formula:
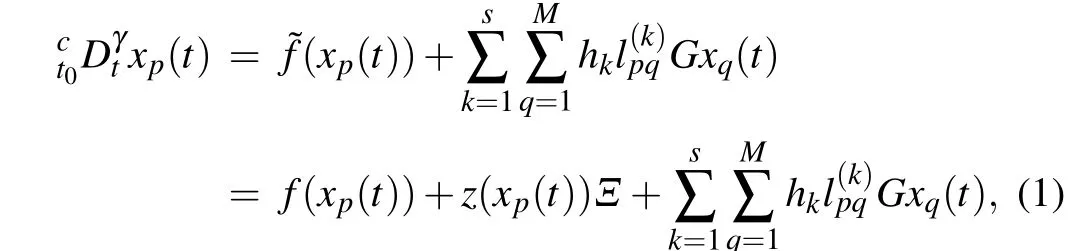




3. Main result
In this section,fractional calculus and the Lyapunov stability theory are used to establish the CNs model,and the sufficient synchronization criteria of FMCNs with uncertain parameters in finite time are obtained.
3.1. Finite-time synchronization of FMCNs with uncertain parameter
Theorem 1 Suppose that Assumptions 1 and 2 are satisfied. If there exist constantε1>0 and gainm*>0 such that



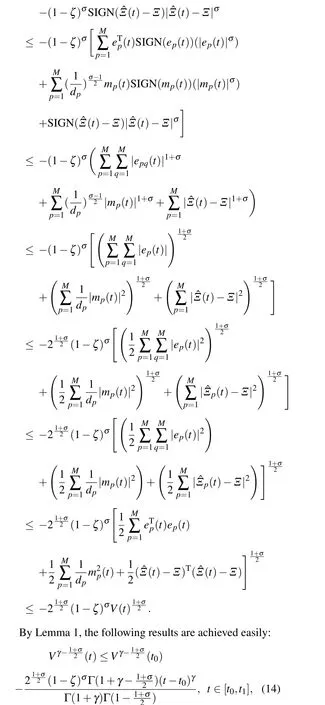
thenV(t)≡0 fort >t1, and the drive and response network can be synchronized in finite timet1, which can be estimated as follows:
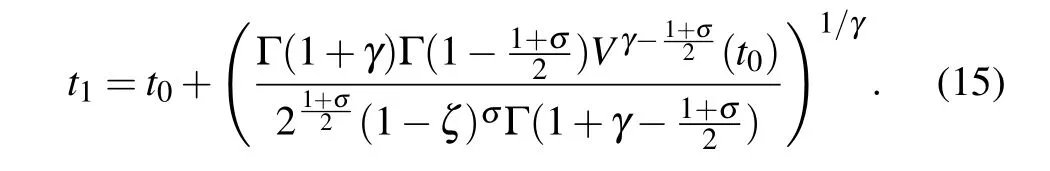
This completes the proof.
3.2. Finite-time synchronization of FMCNs with coupling delay and uncertain parameter
Consider the following FMCNs composing ofMidentical nodes with uncertain parameter and coupling delay described by
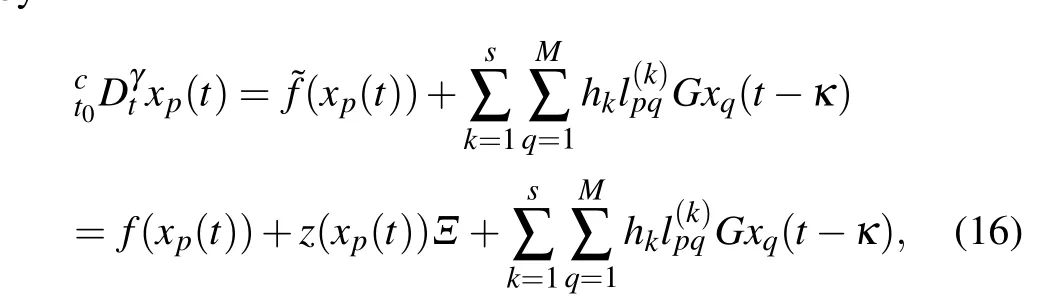
whereγ ∈(0,1),xp(t) = (xp1(t),xp2(t),...,xpm(t))T∈Rm,(p= 1,2,...,M) represents the state vector ofp-th node,f(xp(t)) : Rm →Rmare continuous functions andz(xp(t)) :Rm →Rmare continuous function matrix.Ξ ∈Rmrepresents the vector of system uncertain parameters,and ?f(xp(t)):Rm →Rmare continuous vector functions which consists of two parts.hkrepresents the coupling weight value of thekth weight network, andL(k)=(l(k)pq) is the weight matrix ofk-th weight network. If a connection betweenq-th node top-th node (p/=q) exist, thenlpq ≥0, otherwiselpq=0, and the diagonal elementslpp=-∑Mq=1,q/=p lpq,(p=1,2,...,M),G=diag(g1,g2,...,gm)∈Rmis the internal coupling strength matrix andgp ≥0,andκrepresents the coupling delays.
The system (16) can be used as a drive system, and the system(17)can be used as a response system with controller and external disturbance,which is formulated in the following way:


where ?Ξ(t) denote the estimations of uncertain parameterΞ,ε2anddpare positive constants,andσ ∈(0,γ),then the finite timet2is estimated by

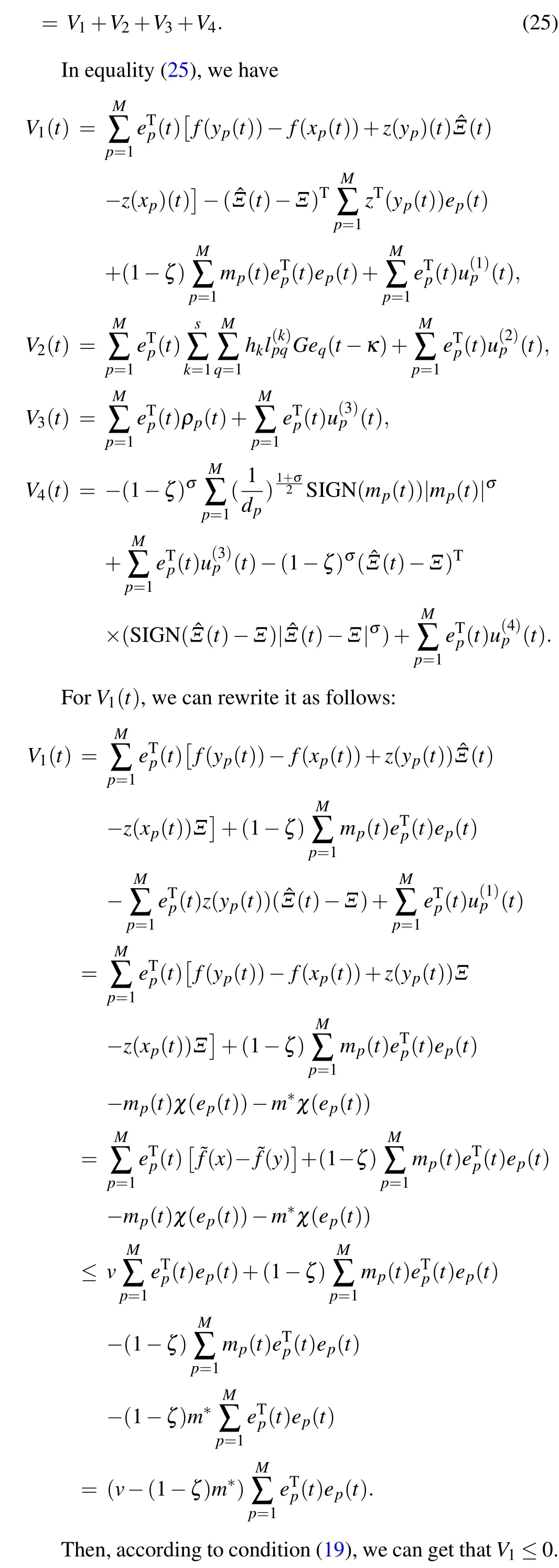
thenV(t)≡0 fort >t2, and drive and response network can be synchronized in finite timet2, which can be estimated as follows

4. Numerical simulations
This section contains two simulation examples that demonstrate the correctness of Theorem 1 and Theorem 2 respectively.
Example 1 Consider the driver network composed of 4 nodes,each of which is a fractional-order Lorenze system
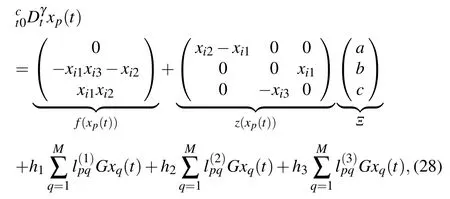
whereγ=0.995,G=diag(1,1,1),h1=0.1,h2=0.2, andh3=0.3,then the chaotic attractor of Lorenze system is shown in Fig. 1. System parameterΞ= (a,b,c)T= (10,8/3,28),xp(0)=(6.2+0.2p,6.4+0.2p,6.6+0.2p)T, (p=1,2,3,4),where three weighted matrices are listed as follows:

Figure 2 depicts the topological structures of network,then the corresponding response network is constructed by the following formula:

where ?Ξ(t)is the estimation for vectorΞ,and external disturbanceρ(t)=(sin(t),cos(t),sin(t)cos(t)).
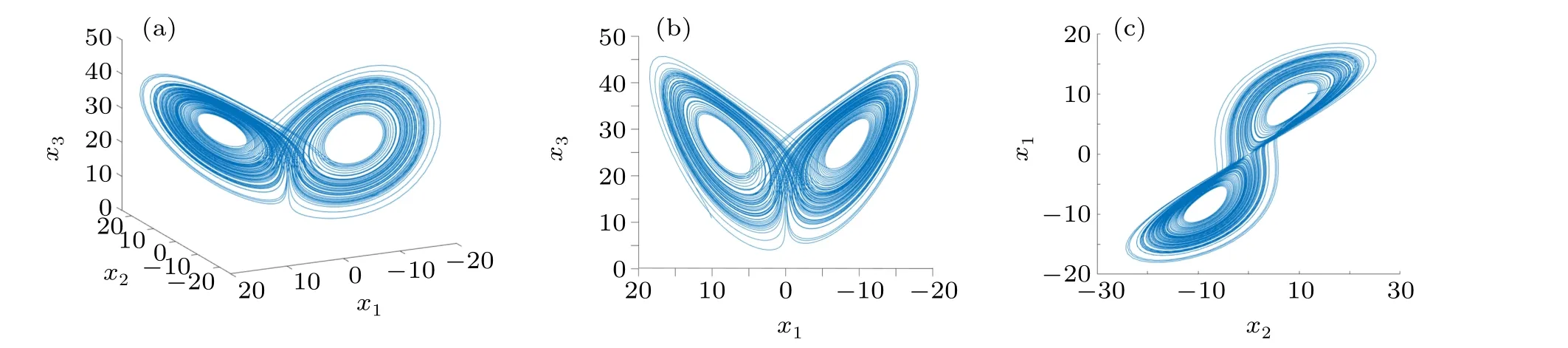
Fig.1. Phase plot of the Lorenze system(γ =0.995).

Fig.2. The topological structures of weighted matrices L(k), k=1,2,3. (a)is matrices L(1),(b)is matrices L(1),and(c)is matrices L(3).


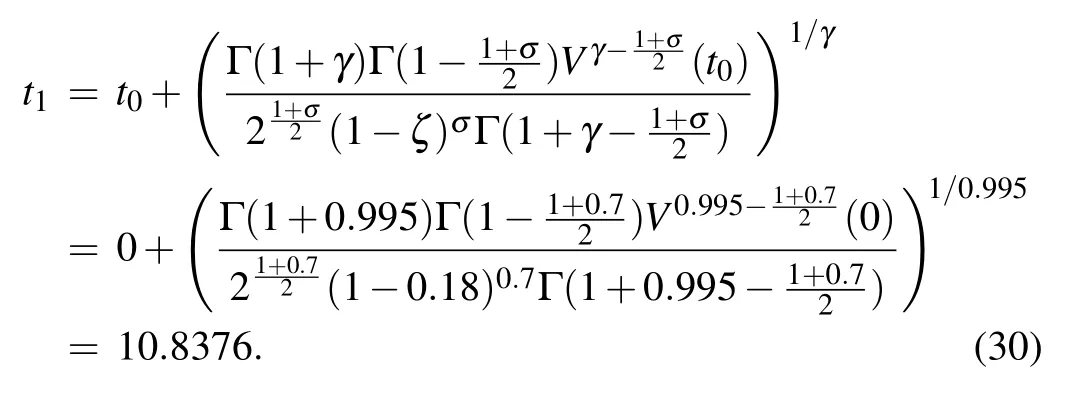
Figure 3 depicts the synchronization errorsep(t)converge to zero, which indicates that synchronization has been realized. Figure 4 shows the synchronization quantized errorsχ(ep(t))converge to zero. Figure 5 displays the identification curve of the uncertain system parameter vectorΞ(t). We can see that the uncertain parameters of the system are successfully identified in finite time. Figure 6 shows the trajectory of adaptive feedback gainmp(t), which converges to zero eventually. Figure 11(a) describes the surface graph of maximum synchronization timet1of Theorem 1 with the change of parameterσand parameterγ.

Fig.3. The ep(t)of the error system.
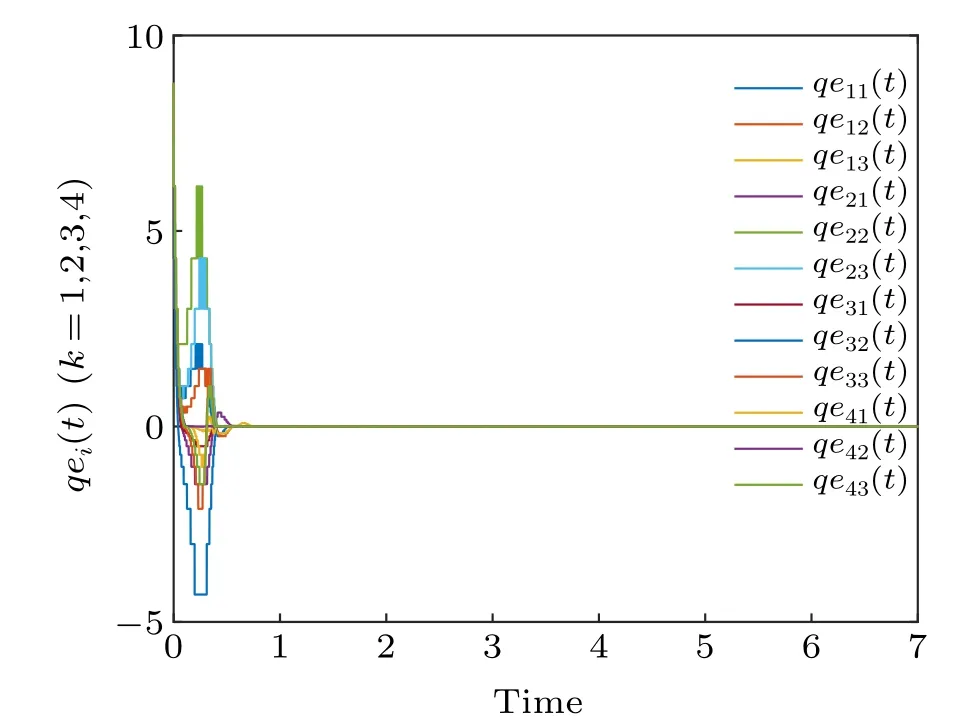
Fig.4. The χ(ep(t))of the error system.
Fig.5. The feedback gain mp(t), p=1,2,3,4 of the adaptive controller.

Fig.6. Identification of the system parameter Ξ.
Example 2 The uncertain FMCNs with coupling delayκ=0.1 are considered, and the drive network can be shown as


By Theorem 2, whent >t2, the response network (17)can synchronize with drive network (16), and the timet2can be estimated as follows:
When synchronization is implemented, both synchronization errorep(t) and synchronization quantization errorχ(ep(t))converge to zero, as shown in Figs.7 and 8,respectively. Figure 9 shows the identification curve of the uncertain system parameter vectorΞ(t), and it can be seen that in the case of coupling delay,the uncertain parameters of the system are still identified correctly. Figure 10 shows the trajectory of adaptive feedback gainmp(t), which also converges to zero eventually. Figure 11(b)describes the surface graph of maximum synchronization timet2of Theorem 2 with the change of parameterσand parameterγ.
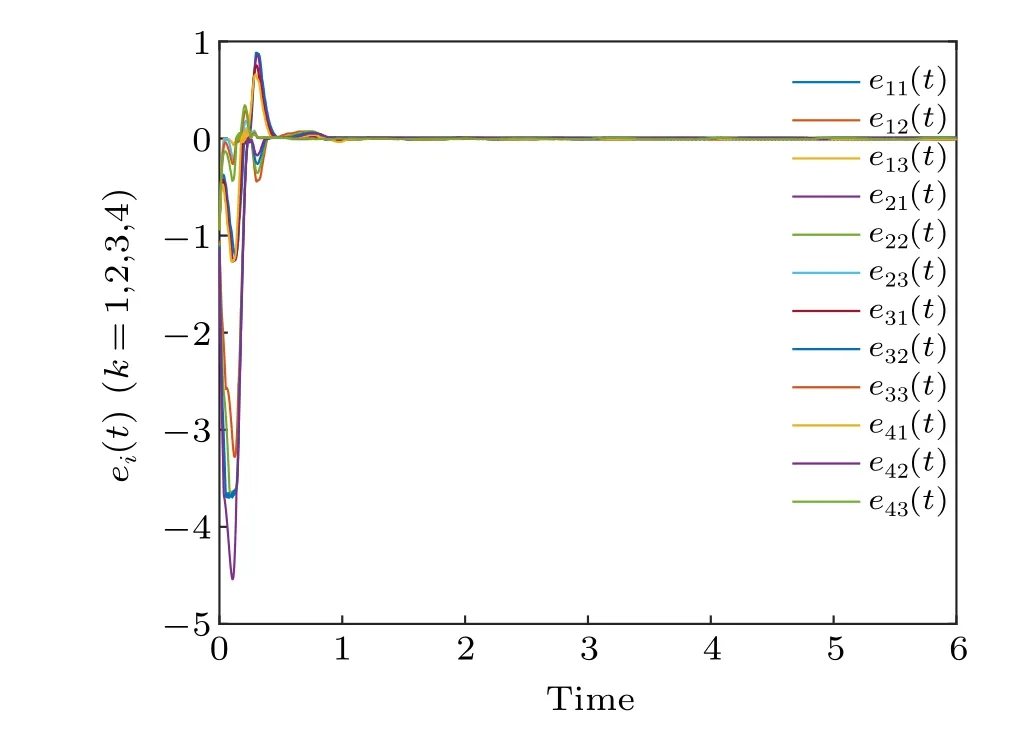
Fig.7. The ep(t)of the error system with coupling delay κ =0.1.

Fig.8. The χ(ep(t))of the error system with coupling delay κ =0.1.
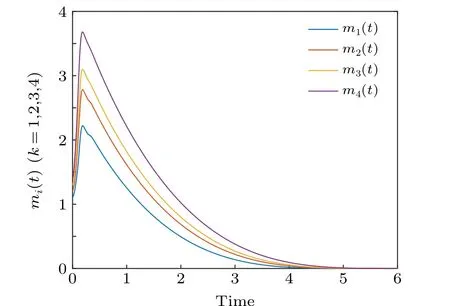
Fig.9. The feedback gain mp(t), p=1,2,3,4 of the adaptive controller with coupling delay κ =0.1.
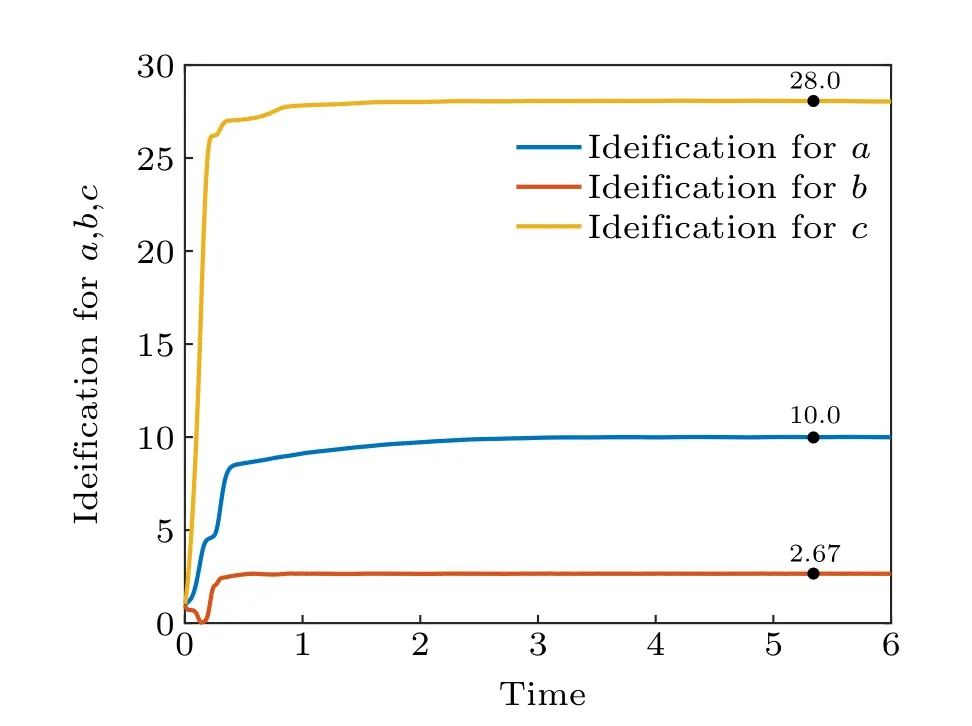
Fig. 10. Identification of the system parameter Ξ with coupling delay κ =0.1.

Fig.11. (a)Setting time t1 of Theorem 1,(b)setting time t2 of Theorem 2.
5. Conclusion
This paper is engaged in the finite-time synchronization problem of FMCNs with uncertain parameters and external disturbances.Firstly,considering the two different cases of nocoupling delay and coupling delay,the corresponding adaptive quantized controller is designed to solve this problem. Then fractional calculus and Lyapunov stability theory are used to obtain theoretical results related to finite-time synchronization and parameter identification.It is worth noting that the time required for parameter identification and network synchronization can be estimated. Finally, numerical simulations of several chaotic systems are given, demonstrating the correctness and effectiveness of the theorem we obtained.Our future work will focus on designing appropriate quantization controllers to solve exponential synchronization problems of multi-layer networks.
- Chinese Physics B的其它文章
- Design of vertical diamond Schottky barrier diode with junction terminal extension structure by using the n-Ga2O3/p-diamond heterojunction
- Multiple modes of perpendicular magnetization switching scheme in single spin–orbit torque device
- Evolution of the high-field-side radiation belts during the neon seeding plasma discharge in EAST tokamak
- Phase-matched second-harmonic generation in hybrid polymer-LN waveguides
- Circular dichroism spectra of α-lactose molecular measured by terahertz time-domain spectroscopy
- Recombination-induced voltage-dependent photocurrent collection loss in CdTe thin film solar cell

