對2022年高考數學全國甲卷一道真題的解讀
?河南省周口市淮陽紅旗中學 余良濤
1 引言
眾所周知,全國卷因覆蓋面廣、重基礎、重能力而精彩,近幾年它又注重對數學本質的考查,使之更具有探究性和挑戰性,集中體現出了“活”的特點.高考命題始終堅持“源于課本,高于課本,不拘泥于課本”的命題導向.筆者在閑暇之余,意外發現了2022年一道高考試題在課本上的“影子”,現結合案例進行解讀,以饗讀者.
2 高考真題呈現
(2022年全國甲卷文科第14題) 設點M在直線2x+y-1=0上,點(3,0)和(0,1)均在⊙M上,則⊙M的方程為________.
3 真題解析
分析:設出點M的坐標,利用點(3,0)和(0,1)均在⊙M上,求出圓心及半徑,即可得圓的方程.
解析:因為點M在直線2x+y-1=0上,所以不妨設點M坐標為(a,1-2a).
又點(3,0)和(0,1)均在⊙M上,則點M到點(3,0)和(0,1)的距離相等且為半徑r.
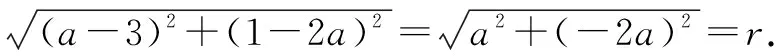
整理,得a2-6a+9+4a2-4a+1=5a2.
解得a=1.
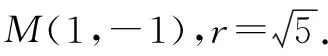
因此,⊙M的方程為(x-1)2+(y+1)2=5.
4 考題出處
筆者通過認真比對,驚奇地發現它的“影子”.它是源自普通高中課程標準實驗教科書(必修)《數學2(A版)》(人民教育出版社,2007年2月第3版)第120頁的例3.題目如下:
已知圓心為C的圓經過點A(1,1)和B(2,-2),且圓心C在直線l:x-y+1=0上.求圓心為C的圓的標準方程.
分析:本題采用2022年全國甲卷的解法肯定是可行的,而教材的解法是采用幾何性質法,即利用“圓中任意弦的垂直平分線必過圓心”“圓內的任意兩條弦的垂直平分線的交點一定是圓心”,然后再利用兩點間的距離公式求出半徑r即可.筆者在這里就不再詳細解答了,具體過程讀者可參考課本例題的解答.
通過以上分析,我們不難發現,2022年全國甲卷這道高考試題是教材例3的“影子”.當然,2022年全國甲卷這道高考題也可采用教材例3的解法求解.筆者在這里真誠地希望讀者要重視“影子”類問題,而教師也更應該重視“影子”類問題的教學.
5 變式探究
這種類型問題除了上述分析中提到的兩種解法外,不妨試想一下它還有沒有其他的解法?因此,我們可以放開手大膽探究一下.下面結合教材中的例3進行解讀.
教材例3體現了是圓的標準方程的靈活應用,特別是要強調圖形在分析問題中的輔助作用.我們知道確定一個圓的要素主要是圓心位置和半徑長.借助圖形再結合題設條件,發現這類問題的關鍵是找出圓心位置,圓心位置一旦確定,就可以利用距離公式求出半徑r,從而再求解.
需要指出的是,在求線段AB的垂直平分線的方程時也可以不求線段AB的中點坐標與直線l′的斜率,而是根據線段垂直平分線的性質“線段垂直平分線上的點到線段兩端點的距離相等”這一結論得到(x-1)2+(y-1)2=(x-2)2+(y+2)2,然后再經過化簡整理可得直線l′的方程為x-3y-3=0.
請讀者記住上述方法,以后我們再求圓的方程就可以采用以上三種方法解答,同時還要密切關注解法的靈活性.
6 自我提升
例題已知圓心C在直線x-2y-3=0上,且過點A(2,-3)和B(-2,-5),求圓心為C的圓的標準方程.
解法1:待定系數法.
設所求圓的標準方程為(x-a)2+(y-b)2=r2.
由題設條件,可得
①
②
③
聯立方程①②③,解得
a=-1,b=-2,r2=10.
故所求圓的標準方程為(x+1)2+(y+2)2=10.
解法2:幾何性質法.
由圓心C在直線x-2y-3=0上,可設點C的坐標為(2t+3,t).
因為該圓經過A,B兩點,所以|CA|=|CB|,即
解得t=-2.
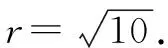
故所求圓的標準方程為(x+1)2+(y+2)2=10.
解法3:幾何性質法.
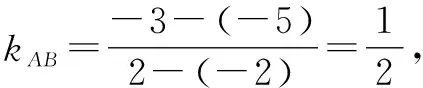
所以,弦AB的垂直平分線的方程為y+4=-2x,即2x+y+4=0.
又圓心C是直線2x+y+4=0與x-2y-3=0的交點,易解得交點坐標為(-1,-2).
所以,圓心C坐標為(-1,-2).
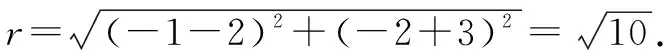
故所求圓的標準方程為(x+1)2+(y+2)2=10.
點評:此題是“一題多解”類問題,通過求解后發現,“待定系數法”思維簡單,運算量較大,但此法易于理解掌握.而“幾何性質法”略顯抽象,掌握起來有一定難度,此法需結合圓的有關性質進行考慮,如垂徑定理等.但這兩種解法備受命題人青睞,請讀者一定要掌握.
你真的掌握了嗎?下面兩個題目讀者不妨嘗試一下.
(1)(2001年全國高考題改編)過點A(1,-1),B(-1,1)且圓心在直線x+y-2=0上的圓的方程是.
分析:對于求解圓的方程問題,我們首先要善于挖掘題設條件中隱含的幾何要素,即圓心坐標和半徑長,但圓心坐標的確定是難點,通常確定圓心位置在弦的垂直平分線上、直徑的中點上或中心對稱點上等等,再利用兩點間距離公式求半徑長即可.
(2)(2019年甘肅酒泉中學二模)已知圓M與直線x-y=0及x-y+4=0都相切,且圓心在直線y=-x+2上,則圓M的標準方程為.
分析:根據題設條件很容易想到設出圓心M的坐標,然后利用圓心M到兩直線距離相等,建立等量關系式,求出圓心M的坐標,從而解出圓M的半徑即可.
上述兩個題目,請讀者自行完成.可以結合本文所述的內容,做好解題反思,因為它們都具備一定的“模型化”和“套路化”的特點,所以以后要注意“影子”類問題,深刻理解,靈活把握,從而達到“舉一反三”的效果.
7 解讀啟示
通過以上解讀,我們知道數學因“問題”而生,探究因“問題”而明,課堂因“問題”而精彩.筆者建議教師要做到:課前帶著“問題”精備,課上帶著“問題”精講,課后帶著“問題”精練,促使“問題”式探究教學法貫穿教學始終,有效穿插“一題多解”“一題多變”“一題多問”“一題多聯”等多種解題方法的靈活運用,穩步提高教學效果.

