函數巧同構 導數妙應用
?東營市第一中學 張琳琳
1 引言
同構意識是破解一些相關數學問題比較常用的一類解題意識與技巧.特別在解決一些函數與方程、不等式等相關問題時,結合相關關系式進行合理轉化或變形,提取出其中相同或相似的結構,尋找結構的同型或共性,進而合理同構相應的函數模型,結合導數的應用來解決相應的數學問題.
2 導數妙用
2.1 巧求范圍
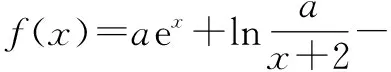
分析:結合條件中不等式的恒等變形與轉化,使不等號兩邊的結構均衡、同型,從而合理同構函數,通過求導,結合函數的單調性與最值的應用來確定對應的參數的取值范圍.
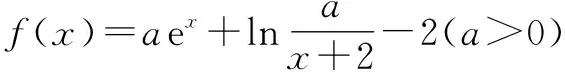
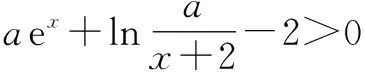
所以ex+lna+x+lna>x+2+ln(x+2),即ex+ln a+x+lna>eln(x+2)+ln(x+2).
由于函數y=ex+x在R上單調遞增,則有x+lna>ln(x+2),即lna>ln(x+2)-x.
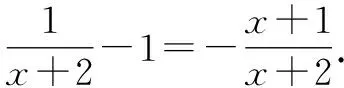
當x∈(-2,-1)時,g′(x)>0,函數g(x)單調遞增;當x∈(-1,+∞)時,g′(x)<0,函數g(x)單調遞減.
故lna>gmax(x)=g(-1)=1,即a>e.
所以實數a的取值范圍為(e,+∞).
故填答案:(e,+∞).
點評:在解決一些相關含參不等式恒成立問題時,往往可以考慮從函數自身出發,巧妙恒等變形,合理同構相應的函數,利用導數及其應用,結合函數的單調性去分析與解題,簡潔自然.
2.2 妙判大小
例2(2022屆江蘇省南師附中、淮陰中學、天一中學、海門中學四校高三年級12月聯考數學試卷·8)已知a=5,b=15(ln 4-ln 3),c=16(ln 5-ln 4),則( ).
A.a C.b 分析:結合三個數所對應的關系式的合理恒等變形,先結合重要不等式性質確定a與b的大小;再通過同構函數,結合求導處理與轉化,利用函數的單調性來確定b與c的大小. 綜上可得,a>b>c.故選擇答案:B. 點評:在判斷一些比較復雜的代數式的大小關系問題時,可以考慮從對應代數式的共同特征入手,合理同構函數,借助同構函數來構造相應的新函數,利用函數的單調性等基本性質來巧妙轉化,進而判斷大小,從而將原問題中所蘊含的內在規律外顯化,揭示問題豐富的背景和內涵,展示同構函數的巨大魅力. 例3[2022屆江蘇省G4(蘇州中學、常州中學、鹽城中學、揚州中學)高三年級12月聯考數學試卷·8改編]若不等式2ex-2>-aln(x+1)+(a+2)x對x∈(0,+∞)恒成立,其中e為自然對數的底數,則實數a的最大值為______. 分析:根據題目條件中的不等式加以移項變形,合理同構函數,結合重要不等式性質確定自變量的大小關系,進而確定函數的單調性,結合求導處理,利用導函數所對應的不等式恒成立來構建不等式,進而確定參數的最大值. 解析:由2ex-2>-aln(x+1)+(a+2)x,移項可得2ex-ax>-aln(x+1)+2(x+1),整理可得 2ex-ax>2eln(x+1)-aln(x+1). 同構函數f(x)=2ex-ax,則有 f(x)>f(ln(x+1)). 而結合重要不等式性質“對于x>0恒有lnx≤x-1,當且僅當x=1時等號成立”,可得x>ln(x+1)>0,則知函數f(x)=2ex-ax在(0,+∞)上單調遞增. 求導可得f′(x)=2ex-a,則只需f′(x)=2ex-a≥0在(0,+∞)上恒成立,所以2-a≥0,解得a≤2. 故實數a的最大值為2.故填答案:2. 點評:在確定一些參數的最值時,關鍵是利用不等式的巧妙變形與轉化,合理同構函數,借助函數的圖象與性質,合理構建相應代數式的大小關系,為進一步求解代數關系式或參數的最值提供條件.在解決此類問題時,對于等式、不等式不同視角的變形,不同的同型形式往往可以同構不同的函數. 例4(2021年高考數學新高考Ⅰ卷第22題)已知函數f(x)=x(1-lnx). (1)討論f(x)的單調性; 分析:第(1)問首先求得導函數的解析式,結合導函數的正負取值符號即可確定函數的單調性;第(2)問利用同構關系將原問題中不等式的證明轉化為極值點偏移的問題,結合變形的關系式的特征同構相應的函數,結合求導處理,利用函數的單調性與極值問題來證明對應的不等式. 解析:(1)由函數的解析式可得f′(x)=-lnx. 則當x∈(0,1)時,f′(x)>0,f(x)單調遞增;當x∈(1,+∞)時,f′(x)<0,f(x)單調遞減. 所以,f(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減. 由(1)可知函數f(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減,所以fmax(x)=f(1)=1,且f(e)=0. 先證2 令函數h(x)=f(x)-f(2-x),x∈(0,1). 求導可得h′(x)=f′(x)+f′(2-x)=-lnx-ln(2-x)=-ln[x(2-x)],則h′(x)在(0,1)上單調遞減. 所以h′(x)>h′(1)=0,即函數h(x)在(0,1)單調遞增.所以h(x1) 再證x1+x2 同理,根據(1)中函數f(x)的單調性,可知即證f(x2)=f(x1)>f(e-x1). 同構函數φ(x)=f(x)-f(e-x),x∈(0,1). 求導可得φ′(x)=-ln[x(e-x)].令φ′(x0)=0.則當x∈(0,x0)時,φ′(x)>0,φ(x)單調遞增;當x∈(x0,1)時,φ′(x)<0,φ(x)單調遞減. 又0 故x→0,φ(0)>0,φ(1)=f(1)-f(e-1)>0. 所以φ(x)>0恒成立,即x1+x2 點評:在證明一些不等式時,經常借助所要證明的不等式的結構特征,合理同構對應的函數,結合函數的導數及其應用,利用相應函數的單調性、極值或最值,進而合理轉化巧妙證明相應的不等式. 在破解一些函數與方程、不等式等相關問題時,需要借助我們的慧眼去識別問題中代數式等的結構特征,尋找同型,巧妙同構,證實共點,妙用共性,合理同構相應的函數模型,結合導數及其應用來巧妙解決,從而實現應用共性解題,增強化歸思想、創新意識、同構意識,合理進行數學知識交匯,讓數學思維與數學品質得以飛躍,形成數學能力,培養數學核心素養.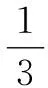
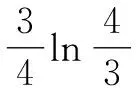
2.3 巧定最值
2.4 妙證不等式
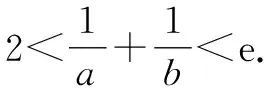
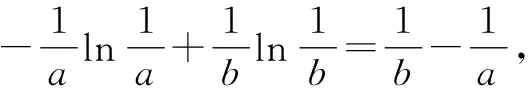
3 結語

