巧思妙法,破解不等式“恒成立”問題
?甘肅省天水市張家川回族自治縣第三高級中學 范 烯
涉及不等式“恒成立”的問題,是高中數學函數與不等式的一個重點與難點,往往以含參不等式的形式出現,是一類極具交匯性、綜合性與創新性的復雜應用問題,難度較大,形式多樣.不等式“恒成立”問題知識融合性強,解決時有一定的經驗規律與技巧方法可循,能有效考查學生各方面的數學基礎知識、數學思想方法與數學能力等,具有較好的選拔性與區分度,倍受各方關注.
1 利用判別式法解決不等式“恒成立”問題
判別式法是通過引入參數進行待定系數法轉化,利用二次方程有根來合理構建判別式,進而結合不等式的求解來分析與解決.
例1對于任意的正數a,b,不等式(2ab+a2)k≤4b2+4ab+3a2恒成立,則實數k的最大值為________.
分析:根據題目條件等價轉化對應的“恒成立”不等式,構建涉及分式不等式的恒成立問題,轉化為關于b的二次方程,利用方程有根并結合判別式構建對應的不等式,通過不等式的求解來確定參數的最值,進而得以確定實數k的最大值.
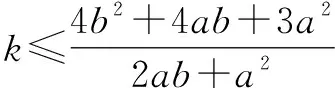
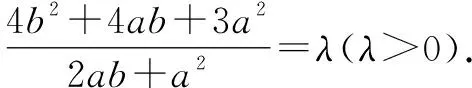

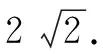
點評:利用判別式法解決不等式“恒成立”問題,關鍵是通過不等式的恒等變換等進行處理,巧妙引入參數轉化為涉及某一變元的一元二次方程,利用方程有實根所對應的判別式非負來構建不等式,進而確定參數的取值范圍,從而得以解決相應的不等式“恒成立”問題.
2 利用數形結合法解決不等式“恒成立”問題
數形結合法的關鍵就是將“恒成立”不等式合理轉化為一個常規函數或一個含參函數的問題,通過函數圖象的“形”來直觀分析與處理.
例2已知函數f(x)=ex-mx,當x>0時,(x-2)f(x)+mx2+2>0恒成立,則實數m的取值范圍為________.
分析:據題目條件對相應的不等式進行等價化歸與轉化,結合參變分離法進行處理,并通過構造兩個函數,把對應的函數的“數”轉化為兩個函數圖象的“形”的問題,進而數形結合,考察含有參數的動直線與定曲線的位置關系,從而建立相應的關系式來確定對應的參數值.
解析:由(x-2)f(x)+mx2+2>0,得(x-2)·ex>-2mx-2,則問題等價于“當x>0時,(x-2)ex>-2mx-2恒成立”.

圖1
構造g(x)=(x-2)ex,h(x)=-2mx-2.
如圖1所示,根據條件,只要考察當x>0時,曲線g(x)=(x-2)ex的圖象恒在直線h(x)=-2mx-2的上方即可.
對g(x)求導,可得g′(x)=(x-1)ex.
當x∈(0,1)時,g′(x)<0,g(x)單調遞減;當x∈(1,+∞)時,g′(x)>0,g(x)單調遞增.
又當x∈(0,+∞)時,g″(x)=xex>0,所以g(x)在(0,+∞)上是凹函數.
而g(0)=h(0)=-2,所以只要滿足直線h(x)=-2mx-2的斜率不大于曲線g(x)=(x-2)ex在x=0處的切線的斜率即可.
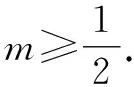


點評:利用數形結合法解決不等式“恒成立”問題,關鍵是結合“恒成立”的不等式進行恒等變形與轉化,構建與之對應的兩個函數,通過一條定曲線與一動直線的位置關系,利用圖形直觀確定臨界位置,這是數形結合處理此類問題的關鍵所在.
3 利用分離參數法解決不等式“恒成立”問題
分離參數法是解決含參不等式“恒成立”問題最常用的一類技巧方法,結合不等式進行恒等變形,分離出相應的參數,再從另一邊所對應的函數來切入與處理.
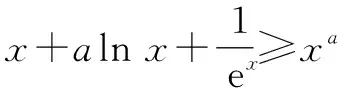
分析:合理結合題目條件中不等式的等價變形與轉化,再結合不等號兩邊的函數結構特征,利用函數的同構處理,通過函數求導確定函數的單調性,進而巧妙分離參數,最后利用函數的構建以及其單調性,進而確定相關參數的取值范圍.
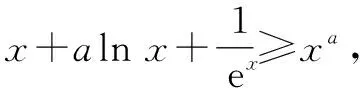
設函數f(x)=x+e-x(x>1),可知f(lnx-a)=lnx-a+e-lnx-a=lnx-a+xa.
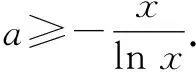

所以函數g(x)在(1,e)上單調遞增,在(e,+∞)上單調遞減.
故g(x)≤g(e)=-e,從而a≥-e.故選擇:C.
點評:利用分離參數法解決不等式“恒成立”問題,關鍵是對含參不等式進行合理恒等變形與轉化,巧妙分離出參數,進而構建對應的函數,通過基本初等函數的單調性或借助函數求導處理來確定對應函數的單調性,進而確定對應函數的極值或最值,從而得以確定參數的取值范圍.
4 利用主參變換法解決不等式“恒成立”問題
主參變換法就是改變常規的主元與參數之間的關系與性質,轉換思維角度,從“旁觀者”的視角來切入,實現問題的化歸與轉化.
例4已知函數y=mx2-mx-6+m,若對于1≤m≤3,y<0恒成立,則實數x的取值范圍為________.
分析:根據題目條件,構建不等式恒成立所對應的不等式,借助主參變換處理,轉化為涉及參數m的一次不等式,利用題目條件以及參數m的限制條件構建涉及參數x的不等式,進而利用題目條件轉化相應的一元二次不等式,通過求解不等式來確定對應實數x的取值范圍.
解析:由y<0,得mx2-mx-6+m<0.借助主參變換處理,整理可得(x2-x+1)m-6<0.
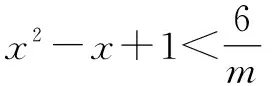
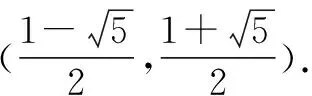
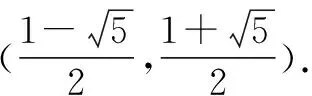
點評:利用主參變換法解決不等式“恒成立”問題,關鍵是利用題目中的不等式進行恒等變形與巧妙轉化,合理轉化主元與參數之間的關系,進行主參變換處理,結合不等式恒成立加以巧妙化歸,進而轉化為不等式、函數等其他相關問題加以分析與處理.
涉及不等式“恒成立”的問題,解決的基本策略就是“含參”轉化與“分參”處理兩個基本思維角度.具體解決時,或通過“數”的視角,利用判別式法、分離參數法、主參變換法等處理;或通過“形”的視角,數形結合法等處理.綜合不等式的性質以及函數的基本性質等,合理構造,巧妙轉化為較為熟悉的數學模型,從而得以破解不等式“恒成立”問題,提升學生數學品質、數學能力,培養數學核心素養.

