函數零點問題解決策略
?四川省達州市第一中學校 向 峰 任宏昇 張 帥
人教版教材必修1第三章“函數與方程”內容體現了聯系與轉化的思想,方程的根、函數的零點、圖象的交點相互化歸轉換,就是將不能直接解決的問題向簡潔、容易解決的問題轉化.教材上明確給出結論:方程f(x)=0有實數解?函數y=f(x)有零點?函數y=f(x)的圖象與x軸有交點.這個結論實質上體現的就是聯系轉化、化歸轉化、數形結合等數學思想,要求學習者綜合運用數學知識,培養轉換思想,開拓解題思路,提高數學能力.
下面結合具體案例,對函數零點問題的解決策略進行探究.
1 轉化為函數圖象與x軸的交點問題
由函數零點定義可知,方程f(x)=0的實數解就是函數f(x)的零點,即為函數y=f(x)的圖象與x軸交點的橫坐標.于是,可直接通過函數f(x)的圖象與x軸的交點情況來研究函數y=f(x)的零點情況.
例1已知函數f(x)=xex-a(lnx+x),a∈R.若f(x)有兩個零點,求實數a的取值范圍.
分析:先研究函數f(x)的特征和性質,得出函數f(x)的圖象,注意函數f(x)的單調區間、極值點、界點,觀察函數f(x)圖象與x軸的交點情況,即可解決問題.
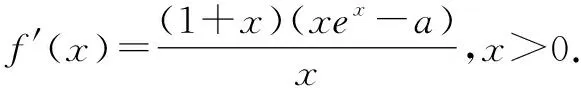
①易知a≤0不合題意.
②當a>0時,設g(x)=xex-a,x>0,則g′(x)=(x+1)ex>0,即g(x)在(0,+∞)上單調遞增.又g(0)=-a<0,當x→+∞時,g(x)→+∞.則存在唯一x0∈(0,+∞),使g(x0)=0,即x0ex0-a=0.當0
則由題意可知,只需
fmin(x)=f(x0)=x0ex0-a(lnx0+x0)<0.又x0ex0-a=0,則只需
a-a(lnx0+x0)=a(1-lnx0-x0)<0.
又a>0,則只需1-lnx0-x0<0.而t(x0)=1-lnx0-x0在(0,+∞)上單調遞減,又t(1)=0,故需x0>1.進而研究a=x0ex0的值域,即可得到實數a的取值范圍是(e,+∞).
2 轉化為函數圖象與直線y=a的交點問題
教材上“函數y=f(x)有零點?函數y=f(x)的圖象與x軸有交點”,體現了將函數y=f(x)有零點轉化為函數y=f(x)的圖象與直線y=0有交點.其中y=0是最為特殊的直線,而在具體問題中,有時候將問題轉化為函數y=g(x)的圖象與直線y=a有交點,解決過程更為簡潔.
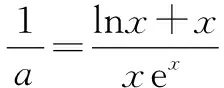
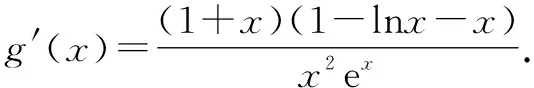
故實數a的取值范圍是(e,+∞).
3 轉化為兩個函數圖象的交點問題
有時候,分析函數結構特征,可將函數y=f(x)的零點問題轉化為方程f(x)=0的實數解問題,再轉化為方程g(x)=φ(x)的實數解問題,最后轉化為函數y=g(x)與y=φ(x)圖象的交點問題.
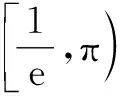
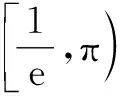
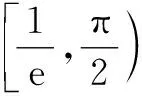
當a=0時,f(x)=xlnx,直接可得零點x=1,符合題意.
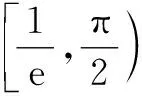
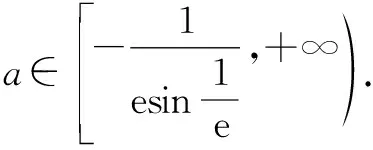
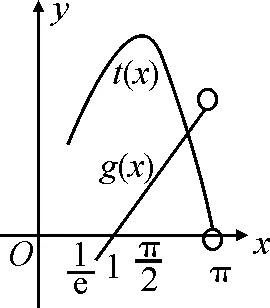
圖1
4 轉化為方程的實數解問題
函數零點問題本質上就是方程的實數解問題.而有的復雜函數對應方程的結構復雜,基本轉化難以解決問題.要先把函數y=f(x)的零點問題轉化為方程f(x)=0的實數解問題,注意等式兩邊構造相同結構;再把方程f(x)=0有實數解轉化為方程g[h(x)]=g[t(x)]有實數解,通過g(x)的單調性把問題轉化為方程h(x)=t(x)的實數解問題,達到化繁為簡,化難為易的目的;最后把方程h(x)=t(x)的實數解問題轉化為函數y=s(x)的圖象與直線y=m的交點問題(或函數y=φ(x)的圖象與x軸的交點問題).
例3已知f(x)=xex+x-axalnx-alnx在(1,+∞)上有零點,求實數a的取值范圍.
分析:此函數結構復雜,直接求導研究單調性困難,不易轉化為函數y=f(x)的圖象與x軸有交點.另外,由于函數結構限制,不能分離參數a,無法轉化為函數y=g(x)的圖象與直線y=a的交點問題,也難以轉化為函數y=g(x)與y=φ(x)圖象的交點問題.這里,f(x)=xex+x-axalnx-alnx有零點等價于方程xex+x=axalnx+alnx有實數解,變形結構,原問題等價于xex+x=(alnx)ealn x+alnx有實數解.根據等式兩邊的結構,設函數g(x)=xex+x,x>1,由函數g(x)單調性可知原問題等價于x=alnx在(1,+∞)上有實數解.
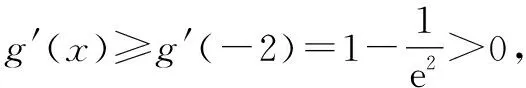
5 轉化為復合函數內外函數的圖象問題
對于復合函數y=f[g(x)]的零點問題,我們可以從內層和外層來認知,設t=g(x),則問題轉化為方程f(t)=0與方程t=g(x)的實數解問題,再在兩個平面直角坐標系中分別作出函數y=f(t)與t=g(x)的圖象,通過觀察兩函數圖象關系即可解決問題.
對于例1,我們通過分析lnx+x與xex的結構,找到聯系,即xex=eln x+x.設t=lnx+x,x>0,則g(t)=et-at,t∈R.而t=lnx+x在(0,+∞)上單調遞增,t和x一一對應,則原問題等價于g(t)=et-at在t∈R上有兩個零點.這種類型問題就是要抓住內外層函數圖象的關聯性,利用兩圖象對應的位置關系解決問題.例1的第三種解法如下:
略解:易知a=0時g(t)=et-at無零點;
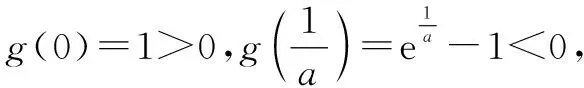
當a>0時,由g′(t)=et-a<0,得t
gmin(t)=g(lna)=a(1-lna).
再以0
不難看出,函數零點個數問題,核心就是考查化歸轉化思想和數形結合思想.具體做法就是把函數零點個數問題轉化為兩個函數圖象交點個數問題.先通過求導(基本函數就不需求導)研究函數的單調性、最大值、最小值、變化趨勢等,按題目要求,畫出函數圖象的走勢規律,標明函數極(最)值的位置,最后借助數形結合思想,觀察兩個函數圖象關系,觀察其交點的個數,其中交點的橫坐標有幾個不同的值,函數就有幾個不同的零點.這樣利用化歸轉化和數形結合的思想方法去處理問題,可以使問題的求解有一個清晰、直觀的整體展現.

