用“點差法”解題,切記嚴謹*
——兼談二次曲線的另一種分類方法
?北京豐臺二中 甘志國
1 引言
“點差法”是平面解析幾何的一種重要解題方法,特別是在求圓錐曲線的中點弦所在直線的斜率時很簡潔且程序化,備受青睞.但筆者欲闡述的觀點是:用“點差法”解題,切記嚴謹!
2 用“點差法”解題,切記嚴謹
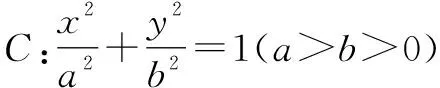
命題者給出的參考答案如下:
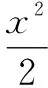
b2(x1+x2)(x1-x2)=-a2(y1+y2)(y1-y2)
①
②

分析:由①到②必須先說明②中的兩個分母均不為0.若x1=x2或y1=-y2,則均可得該橢圓上的兩點A,B關于x軸對稱,這與“點M(-1,1)是線段AB的中點”矛盾!所以②成立.
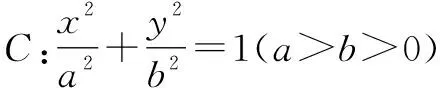
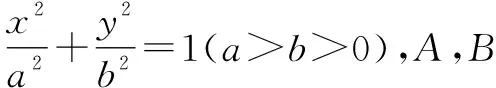
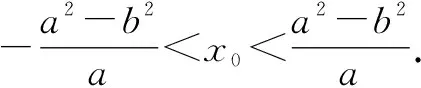
解:設兩點A(x1,y1),B(x2,y2),同題1的“解”可得②成立,所以線段AB的垂直平分線方程為
由線段AB的垂直平分線過點P(x0,0),可得
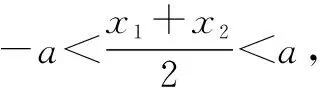
分析:由“線段AB的垂直平分線與x軸相交”可得直線AB的斜率存在,所以②在這里成立(但在解題過程中應交代清楚).
當且僅當直線AB的斜率不為0即x1+x2≠0時③成立,從④推得⑤還要說明y1+y2≠0.當然這可由⑤成立(但在解題過程中應有所交代),此時以上解答正確.
當直線AB的斜率為0即x1+x2=0時,由橢圓的對稱性及“線段AB的垂直平分線過點P(x0,0)”可得x0=0,此時欲證結論也成立.
綜上所述,可得欲證結論成立.
題3[《普通高級中學教科書·必修·數學·第二冊(上)》(人民教育出版社,2006)第133頁第7題的反問題]設直線l與拋物線y2=2px相交于兩點P(x1,y1),Q(x2,y2),若y1y2=-p2,求證:直線l過該拋物線的焦點.
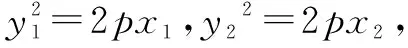
(y1+y2)(y1-y2)=2p(x1-x2) ⑥
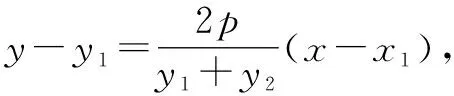
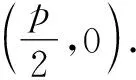
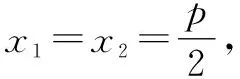
綜上所述,可得欲證結論成立.
總之,用“點差法”解題,切記嚴謹:
(1)把等積式變成比例式時(比如把①變成②,⑥變成⑦),要注意分母不為0(若分母的值為0,則中點弦所在直線的斜率不存在,須另行研究,比如題3);
(2)除非題設中有“中點弦所在的直線與圓錐曲線交于不同的兩點”(比如題2與題3),否則要檢驗中點弦所在的直線與圓錐曲線確實交于不同的兩點(比如題1);
(3)遇到中點弦的垂線問題時,中點弦所在直線的斜率為0的情形要單獨討論,因為此時中點弦的垂線的斜率不存在(比如題2).
3 眾多文獻給出的“二次曲線中點弦所在直線的方程”欠嚴謹
定理1[3][4]設f(x,y)=Ax2+Bxy+Cy2+Dx+Ey+F(A2+B2+C2≠0),若P(x0,y0)是二次曲線f(x,y)=0的弦P1P2的中點,則直線P1P2的方程是
⑧
證法1[3]:設點P1(X,Y),由P(x0,y0)是弦P1P2的中點,可得點P2(2x0-X,2y0-Y).再由兩點P1,P2均在二次曲線f(x,y)=0上,可得
AX2+BXY+CY2+DX+EY+F=0,
A(2x0-X)2+B(2x0-X)(2y0-Y)+C(2y0-
Y)2+D(2x0-X)+E(2y0-Y)+F=0.
把它們相減后再除以4,可得
由此可驗證兩點P1(X,Y),P2(2x0-X,2y0-Y)均在直線⑧上,再由“兩點確定一直線”可得欲證結論成立.
證法2[4]:設兩點Pi(xi,yi)(i=1,2),由P(x0,y0)是弦P1P2的中點,可得x1+x2=2x0,y1+y2=2y0.再由兩點P1(x1,y1),P2(2x0-x1,2y0-y1)均在二次曲線f(x,y)=0上,可得
A(2x0-x1)2+B(2x0-x1)(2y0-y1)+C(2y0-y1)2+D(2x0-x1)+E(2y0-y1)+F=0.
把它們相減后,可得
(2Ax0+By0+D)(x1-x0)+(Bx0+2Cy0+E)·(y1-y0)=0
⑨
再由(x0-x1,y0-y1)是直線P1P2的一個方向向量,可得直線P1P2的一個法向量是(2Ax0+By0+D,Bx0+2Cy0+E),進而可求得直線P1P2的方程是(2Ax0+By0+D)(x-x0)+(Bx0+2Cy0+E)(y-y0)=0即⑧.
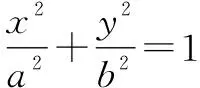
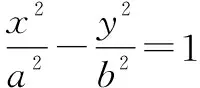
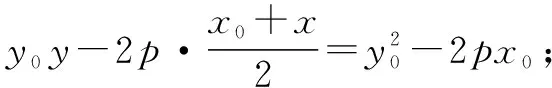
分析:由題文[5]例7(1)及例8(1)的結論可知定理1[3][4]、推論1~3[3]均欠嚴謹,因而,它們相應的證法1[3]、證法2[4]也均欠嚴謹.下面再給予分析.
“定理1[3][4]”及其“證法1[3]”必須建立在“關于x,y的方程⑧確實表示直線”(即
不成立)、“直線⑧與二次曲線f(x,y)=0確實是交于兩個不同的點P1,P2”(否則不能得出“兩點確定一直線”)這兩個前提下才是正確的,否則不正確.
“定理1[3][4]”及其“證法2[4]”必須建立在“直線P1P2的一個方向向量(x0-x1,y0-y1)不是0”[即Pi(xi,yi)(i=1,2)確實是兩個不同的點]、“直線P1P2的一個法向量(2Ax0+By0+D,Bx0+2Cy0+E)不是0”(即不成立)及“關于x,y的方程⑧確實表示直線”(即⑨不成立)這三個前提下才是正確的,否則不正確.
由定理1[3][4]或推論1[3]可得:橢圓4x2+y2-1=0以坐標原點為中點的弦所在直線l的方程是0x+0y=0[而該方程不表示直線.事實上,由文[5]例7(1)及(3)(i)的結論,可得直線l的方程是αx+βy=0(α,β是不同時是0的常數)].由定理1[3][4]或推論2[3]可得:雙曲線4x2-y2-1=0以坐標原點為中點的弦所在直線l的方程是0x-0y=0[而該方程不表示直線.事實上,由文[5]例7(1)及(4)(i)的結論,可得直線l的方程是y=kx(-2 注:若“關于x,y的方程⑧確實表示直線”(即⑨不成立)、“直線⑧與二次曲線f(x,y)=0確實是相交于兩個不同的點”,則定理1[3][4]正確. 定理2[4]若f(x,y)=Ax2+Bxy+Cy2+Dx+Ey+F(A2+B2+C2≠0),則二次曲線f(x,y)=0在點P(x0,y0)處切線方程是 證明[4]:當二次曲線f(x,y)=0的弦P1P2的兩個端點Pi(xi,yi)(i=1,2)重合即三點P1,P,P2重合時,直線P1P2就是曲線f(x,y)=0在點P(x0,y0)處切線.再由f(x0,y0)=0及定理1[3][4],可得欲證結論成立. 分析:因為定理2[4]的證明[4]是建立在定理1[3][4]的前提下的,而定理1[3][4]不嚴謹,所以定理2[4]及其證明[4]均不嚴謹. 由定理2[4]可得:二次曲線y2=0在坐標原點處的切線l的方程是0y=0[而該方程不表示直線.事實上,由導數的幾何意義可知直線y=kx+b(k,b均是常數)在該直線上任意一點處的切線均是該直線本身,可得切線l的方程是y=0].由定理2[4]可得:二次曲線x2-y2=0在坐標原點處的切線l的方程是0x-0y=0[而該方程不表示直線.筆者還不能斷定切線l的方程是什么.有兩種想法:(1)由二次曲線x2-y2=0以坐標原點為中點的弦所在直線是y=x或y=-x及“當中點弦兩個端點重合時的中點弦所在直線是切線”(參見定理2[4]的證明[4]),可認為切線l的方程也是y=x或y=-x;(2)由曲線y=|x|在坐標原點處的切線不存在及曲線x2-y2=0與曲線y=|x|的聯系,可認為切線l不存在]. 注:若“關于x,y的方程確實表示直線”(即不成立)、“直線與二次曲線f(x,y)=0確實相切”,則定理2[4]正確. 證明:設兩個切點分別是Pi(xi,yi)(i=1,2),由定理2[4]可得二次曲線f(x,y)=0在點Pi(i=1,2)處的切線方程是 由點P(x0,y0)同時在這兩條切線上,可得 所以兩點Pi(xi,yi)(i=1,2)均在直線上,再由“兩點確定一直線”可得欲證結論成立. 注:由定理1[3][4]及定理2[4]的“注”可知,定理3[4]及其證明均是嚴謹的. 設f(x,y)=Ax2+Bxy+Cy2+Dx+Ey+F(A2+B2+C2≠0),記 則二次曲線f(x,y)=0的分類結果(共九種)如表1所示[5]: 表1 二次曲線f(x,y)=0分類結果 下面再給出其另一種分類方法及其結果. 參見定理1[3][4]證法2[4]的⑨式,可得二次曲線f(x,y)=0關于點(x0,y0)對稱的充要條件是f(x,y)=f(2x0-x,2y0-y)即(2Ax0+By0+D)(x-x0)+(Bx0+2Cy0+E)(y-y0)=0,也即 也即 (1)當關于x0,y0的方程組有唯一一組解即Δ≠0(參見)時,二次曲線f(x,y)=0(包括軌跡不存在的情形,下同)有唯一的對稱中心(即表1中的前兩個型別也即前五個類別); (2)當關于x0,y0的方程組有無數組解即Δ=Θ=0(參見)時,二次曲線f(x,y)=0有無數個對稱中心且這些對稱中心的集合是直線2Ax+By+D=0(即表1中的后三個類別); (3)當關于x0,y0的方程組無解即Δ=0,Θ≠0(參見)時,二次曲線f(x,y)=0無對稱中心(即表1中的第六個類別).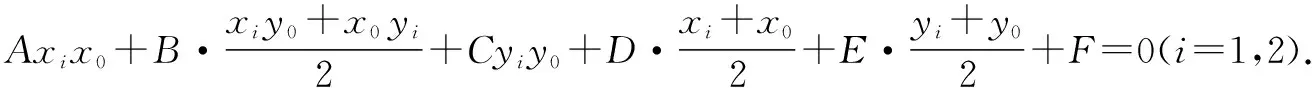
4 二次曲線的另一種分類方法及其結果