基于改進免疫優化算法的冷鏈多式聯運路徑優化研究

段力偉，李震

（重慶交通大學交通運輸學院，重慶 400064）

目前，隨著冷鏈運輸的迅速發展，冷鏈運輸結構單一的問題也愈發明顯。我國冷鏈運輸90%以上由公路完成，而鐵路占比不足1%[1]，同時冷鏈運輸路徑不合理加劇了途中損耗。因此，優化冷鏈市場的運輸結構，發展多式聯運，發揮不同運輸方式的優勢，確保冷鏈貨物的運輸質量，能夠更好地滿足我國不斷增長的冷鏈運輸需求。

多式聯運路徑優化問題是一個NP-hard 問題，已有很多學者對該問題的求解做出了相關研究，如李飄等提出了一種綜合k-最短路徑算法和逼近理想解排序法的混合算法，以求解時變條件下的多目標路徑優化模型[2]；劉雪萍采用了模擬退火算法對多應急救援點、多受災點的救援物資的運送路徑選擇問題進行了研究[3]；劉松在蟻群算法中設計Ant-Cycle 模型來更新信息素，以最短時間為目標解決應急救援物資的路徑優化問題[4]；朱欣媛設計了基于遺傳算法和粒子群算法的混合算法，探討了碳排放約束下的時間模糊路徑選擇問題[5]；Diabat 提出了一種基于禁忌搜索的周期性分配-庫存問題（PDIP）的啟發式算法，該算法性能優于95%以上基于列生成并考慮數據集的啟發式算法[6]。

通過相關文獻可以看出，目前啟發式算法被廣泛應用于求解多式聯運路徑優化問題，然而傳統的啟發式算法存在陷入局部最優解和優化效率低的問題。該文綜合考慮冷鏈多式聯運的特點和影響因素，采用Weibull 三參數分布函數來描述冷鏈貨物運輸途中的變質損耗變化情況，并提出了混合粒子群算法雙尋優的免疫優化算法，對模型進行求解，通過對算例的分析計算表明，優化后的算法能夠有效解決此類問題，并具有更快的收斂速度。

1 冷鏈多式聯運路徑優化模型構建

1.1 問題描述

以集裝箱運送冷鏈貨物，在中途節點可進行運輸方式的中轉，相鄰節點之間有多種運輸方式，中轉會產生相應的時間、費用。同時，由于貨物在途中運輸時間不同，貨物產生的損耗和制冷成本也不同。模型以總成本最小為目標，確定OD 間最佳的運輸路徑，并滿足時限要求。

1.2 條件假設

1）貨物在運輸中始終處在冷藏集裝箱中，作為一個整體不被分開運輸。

2）運輸工具與中轉能力充足，能夠滿足這次運輸。3）貨物在節點能夠及時開始轉運工作。

1.3 符號說明

1.4 模型構建

目前在對多式聯運路徑優化問題的模型構建上，大多采用的是將路段選擇和中轉節點選擇作為規劃路徑的（0，1）變量，以此構建目標函數為總成本最小的整數線性規劃模型[7-8]。該文在現有研究的基礎上，考慮損耗成本和制冷成本，以總物流成本最低，建立多式聯運路徑優化模型，相關成本分析如下：

1）基礎運輸成本CY

在使用運輸工具在路徑上運輸時，基礎運輸費用與所選路徑的運輸距離呈正相關線性關系。

2）中轉成本CZ

當時城市節點中轉變量為1 時，產生中轉成本。

3）損耗成本CS

該文參考Weibull 三參數分布函數來描述冷鏈貨物途中的損耗變化情況，該函數被證明能夠適用于各種情況，如物品的變質損耗情況、電子元件的失效、物品的銷售壽命等[9]，具有極強的普適性，其分布函數如下：

式中，α是函數的尺度因子，α＞0；β是函數的形狀因子，β＞0；γ為函數的位置因子，t為時間。由該分布函數得到貨物的損耗率，以計算損耗成本。

4）時間窗懲罰成本C(t)

約束時間內不收取懲罰費用，貨物提前送達而沒有超出允許最早時間時，收取相應的倉儲費用，其他時間段懲罰成本無限大：

5）制冷成本CL

該文制冷成本參考相關文獻[10-11]中的計算方法，通過計算冷藏車產生的熱負荷換算成制冷所產生的燃油消耗，熱負荷來源于車廂內外溫度差，計算公式為：

其中，S為箱體表面積，通常通過車廂內表面積和外表面積求出，即。

根據以上各成本分析，加入相關約束條件，即可建立如下的冷鏈路徑優化模型：

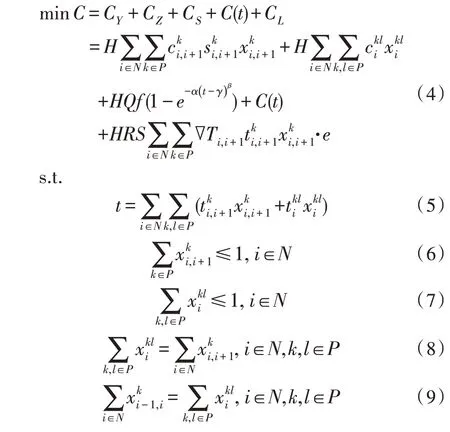
其中，式（4）為目標函數；式（5）表示總運輸時間；式（6）為運輸方式限制；式（7）為轉運次數約束；式（8）-（9）為前后選擇平衡約束。

2 算法設計

2.1 算法簡介

免疫優化算法是利用免疫系統的多樣性和維持機制來保持群體的多樣性，并強調群體中個體間的信息交換，從而實現對解空間搜索的一種智能計算方法[12]，在實際求解時，雖然將優秀抗體保存到記憶細胞中，使迭代全程收斂，但未能避免單個抗體的退化現象，使得算法的收斂速度受到影響。基于此，該文參考粒子群算法中雙尋優的特性，創建個體最優抗體庫，在每一次迭代中更新每一個抗體所經歷的最優位置，并將其與每代形成的新抗體進行適應度值比較，從而更新抗體群，加快算法的收斂速度。

2.2 求解步驟

1）抗體編碼。城市節點選用0 和1 編碼，即經過該城市為1，否則為0；運輸方式用1、2、3 進行編碼，分別代表公路、鐵路、水路。進行F 次編碼初始化F 個抗體形成初始抗體群。抗體的編碼示意圖如圖1 所示。

圖1 粒子編碼示意圖

2）抗體的多樣性評價。抗體適應度Av：將適應度函數設置為目標函數的倒數，并初始化抗體個體最優庫。

抗體相似度Simv,s：當兩個抗體編碼中相同編碼的位數大于設定的閾值ps，則表示這兩種抗體相似。

抗體濃度Conv：由抗體與抗體之間的相似度來計算，每個抗體的濃度為群體中與該抗體相似個體占群體總數的比例。

期望繁殖概率：由抗體的適應度值和濃度計算每個抗體的期望繁殖概率，即：

其中，Av為抗體v的適應度值，θ為多樣性評價參數。

形成父代群體：將抗體中期望繁殖概率最高的r個抗體存入記憶庫中作為記憶細胞，期望繁殖概率最高的（F-r）個抗體構成父代群體。

3）遺傳操作。遺傳操作包括選擇、交叉和變異。

4）更新抗體群。計算經過遺傳操作形成的子代群體和記憶細胞的適應度值，更新抗體的個體最優庫，并從個體最優中找出適應度最大的群體最優抗體并記錄。將子代細胞的個體最優與記憶細胞結合生成新的抗體群，返回步驟2）進行下一次迭代。滿足終止條件時，輸出記錄的群體最優抗體適應度值。

3 案例分析

3.1 案例設計

現假設有櫻桃、海蝦、柑橘三種農產品在運輸網絡中流通，運輸具體信息如表1 所示，運輸途中的損耗參數參考相關文獻[11,13-14]。提前到達的貨物將收取100 元/t·h 的倉儲費用。制冷費用參數[13]中熱傳率R為2.49 kCal/（h·m2·℃），車廂內表面積為22.70 m2，外表面積24.67 m2，單位制冷成本e為1 元/kCal。

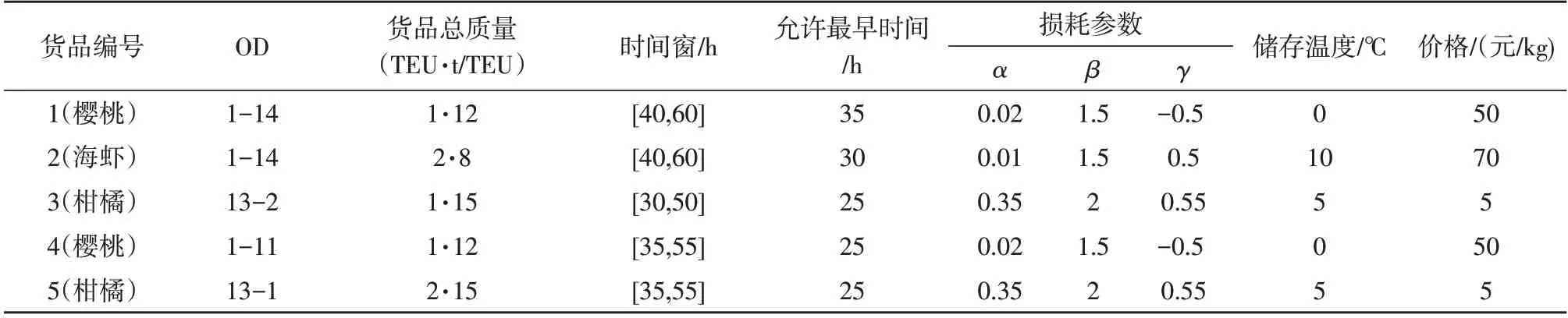
表1 冷鏈貨物運輸信息表

運輸網絡共有14 個節點城市，如圖2 所示。各節點運輸距離和各運輸方式轉運信息如表2 所示，各運輸方式的具體參數如下：公路運輸平均速度為90 km/h，費率為9.39 元/（TEU·km），鐵路運輸平均速度為60 km/h，費率基價一為572 元/（TEU·km），基價二為4.14 元/（TEU·km），水路運輸平均速度為40 km/h，費率為2.34 元/（TEU·km）；公路與鐵路、水路互相轉運的費用分別為150元/TEU、225元/TEU，時間都為0.5 h，鐵路和水路轉運的費用為826 元/TEU，時間為1 h。

表2 節點間路段各運輸方式運輸距離

圖2 運輸路徑網絡

3.2 案例求解

利用數學軟件Matlab 對算例進行求解，設抗體種群規模為80 個，記憶庫容量為20 個，交叉概率0.7，變異概率0.5，相似度閾值ps 為0.8，多樣性評價參數θ為0.95，迭代次數100 次。同時，選用第一批貨物為例使用免疫優化算法與改進后的算法進行對比，如圖3 所示，路徑優化結果見表3。

表3 路徑優化結果

圖3 算法迭代對比圖

從圖3 可以看出，改進的免疫優化算法可以通過對抗體染色體的變化，來描述運輸方式和路段的選擇優化，能夠有效契合多式聯運路徑優化問題；與原算法相比，改進后的算法具有更快的收斂速度和更好的收斂效果。

4 結論

該文采用Weibull 分布函數來描述不同類型產品的損耗率，并構建冷鏈多式聯運路徑優化模型，進而利用粒子群算法雙尋優的特點，對免疫優化算法進行改進，從而加快了算法的收斂速度。最后通過多OD 的算例進行模擬，結果證明改進后的算法能夠有效地解決多式聯運路徑優化問題，并具有較快的收斂速度，同時在考慮損耗因素時，選用的Weibull三參數分布函數也能夠對不同貨物的損耗狀況進行描述，具有很好的適用性。