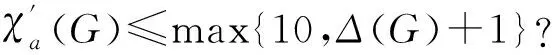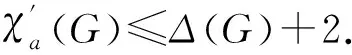無相鄰3-圈平面圖的鄰點可區別邊染色

蔡洪鋒, 黃丹君

(浙江師范大學 數學與計算機科學學院,浙江 金華 321004)

0 引 言

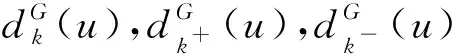
Zhang等[1]在2002年提出圖的鄰點可區別邊染色這一概念,并對一些特殊圖類(樹、路、圈、完全圖、完全二部圖等)的鄰點可區別邊色數進行了刻畫.基于這些結果,他們給出了關于圖的鄰點可區別邊染色問題的猜想.

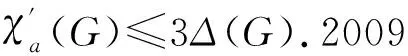
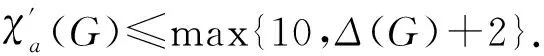
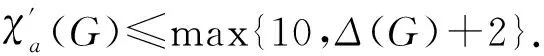
1 定理1的證明

假設G是定理1中關于邊數達到最小的一個極小反例.顯然,G是連通的.先分析G的結構性質,再運用權轉移方法得出矛盾,從而定理1得證.令T(G)=max{10,Δ(G)+2},C={1,2,…,T(G)}表示顏色集合.顯然|C|≥10.

斷言1[15]圖G中1-點不與5--點相鄰.

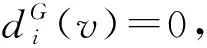
注2設uv∈E(G)為G中的輕k-邊,k∈{2,3,4}.若H=G-uv存在一個T(G)-avd-邊染色φ且Cφ(u)≠Cφ(v),則|C(Cφ(u)∪Cφ(v))|≥10-2(k-1)≥4.由斷言2知,?α∈C(Cφ(u)∪Cφ(v)),使得邊uv可染α色且滿足u不與NG(u)中的點沖突,v不與v的鄰點沖突.因此,可以將φ擴染為G的一個T(G)-avd-邊染色.

證明記NG(v)={v1,v2,…,vk},NG(v1)={v,v2,u1,u2}且NG(v2)={v,v1,w1,w2}.令H=G-v1v2.由注1知,H有一個T(G)-avd-邊染色φ.設φ(vvi)=i,i∈[1,k].

先證:若G中存在(4,4,k)-圈v1v2vv1,則k≥7.用反證法.假設k≤6.由斷言2和斷言3知,k=6.由注2知,Cφ(v1)=Cφ(v2).不妨設Cφ(v1)=Cφ(v2)={1,2,a}且a∈[3,7].可以用{8,9,10}中的任意一種顏色改染vv1或vv2,導出v的6個不同的顏色集合，而v至多只有4個沖突點，所以必存在一種改染方式φ′,使得v不與其鄰點產生沖突且Cφ′(v1)≠Cφ′(v2).由注2知,φ可以擴染為G的一個T(G)-avd-邊染色.矛盾.

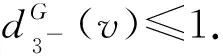
斷言6設dG(v)=7,則

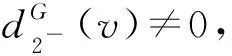
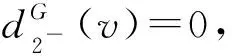
3)v不與(3,3,7)-圈關聯.

證明令NG(v)={v1,v2,…,v7}.由文獻[15]的斷言6知,1)成立.

3)用反證法.假設v與(3,3,7)-圈關聯.設dG(v1)=dG(v2)=3且v1v2∈E(G).令H=G-v1v2.由注1知,H有一個T(G)-avd-邊染色φ.設φ(vvi)=i,i∈[1,7].由注2知,Cφ(v1)=Cφ(v2)={1,2}.用{8,9,10}中的任意一種顏色改染vv1或vv2,得到v的6個不同的顏色集合.而v至多只有5個沖突點，所以必存在一種改染方式φ′,使得v不與其鄰點產生沖突且Cφ′(v1)≠Cφ′(v2).由注2知,φ可以擴染為G的一個T(G)-avd-邊染色.矛盾.斷言6證畢.

斷言7設dG(v)=k且k≥8,則

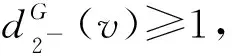
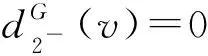
證明記NG(v)={v1,v2,…,vk}.

2)設dG(v1)=dG(v2)=3且v1v2∈E(G).令H=G-v1v2,由注1知,H有一個T(G)-avd-邊染色φ.設φ(vvi)=i,i∈[1,k].由注2知,Cφ(v1)=Cφ(v2)={1,2}.

3)設dG(v1)=dG(v2)=4且v1v2∈E(G).令H=G-v1v2,由注1知,H有一個T(G)-avd-染色φ.設φ(vvi)=i,i∈[1,k].由注2知,Cφ(v1)=Cφ(v2)={1,2,a}.

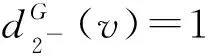
令H為G中刪去所有2--點所得到的點數最多的一個連通分支,因此,δ(H)≥3且H是無相鄰3-圈的平面圖.根據斷言1和斷言5～斷言7可推斷出dG(v)和dH(v)的關系如表1所示.

表1 dG(v)和dH(v)之間的關系

斷言81)若dH(v)=k且3≤k≤4,則dG(v)=dH(v);

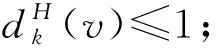
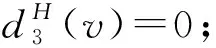
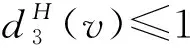
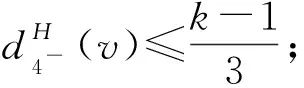
9)任意3-面f至少關聯1個5+-點v.

證明根據表1和斷言1～斷言3可知,1)～3)和9)顯然是正確的.

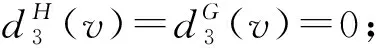
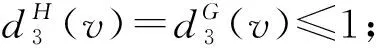
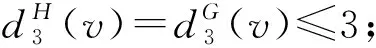
下面利用權轉移方法推出矛盾.首先,對任意x∈V(H)∪F(H),定義初始權函數w(x)=dH(x)-4.根據歐拉公式|V(H)|-|E(H)|+|F(H)|=2,有

下面定義適當的權轉移規則.在權轉移過程中,總權和保持不變.記新的權函數為w′(x),x∈V(H)∪F(H).若能證明對任意x∈V(H)∪F(H),有w′(x)≥0,則有如下矛盾:

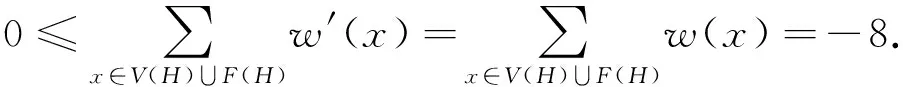
因此,圖H不存在,從而極小反例圖G不存在,即定理1成立.

定義如下權轉移規則:

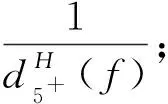
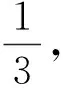
下面證明對?v∈V(H),有w′(v)≥0.

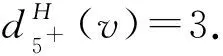
設dH(v)=4.則w′(v)=4-4=0.

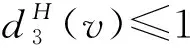
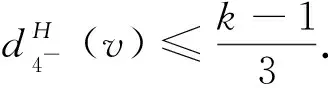
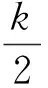
因此,完成了定理1的證明.

2 結 語