關節臂式坐標測量機熱誤差仿真建模及補償

曾志江，高貫斌，馬文金

（650500 云南省 昆明市 昆明理工大學 機電工程學院）

0 引言

隨著現代制造水平的不斷提高，對精密儀器的精度要求也越來越高，溫度變化對精密儀器的測量精度影響十分顯著[1]。關節臂式坐標測量機是一種新型的多自由度非正交式坐標系測量機，由于其靈活性高和便攜性好，現已逐步應用于航空航天、機械制造、汽車船舶等領域。測量精度是制約關節臂式坐標測量機發展的一個主要因素，溫度變化帶來的熱變形誤差是影響關節臂式坐標測量機精度的重要因素[2-3]，采取相應措施減小其影響對提高關節臂式坐標測量機的精度具有重要意義。

由于熱誤差補償研究對硬件條件要求高，且需要長時間、大數據樣本的測試分析，目前關節臂式坐標測量機熱誤差研究的文獻較少。Santolaria[4]等在不同的溫度下對關節臂式坐標測量機的運動學參數進行辨識，以20 ℃下的運動學參數作為參考基準值，采用四次多項式擬合預測其它溫度下運動學參數相對于參考值的偏差，并補償到關節臂式坐標測量機的控制器中，實現熱誤差補償。胡毅[5]通過對一標準桿件的長度測量，分析了在環境溫度改變及內部熱源對測量精度的影響，并建立了基于神經網絡的補償模型對關節臂式坐標測量機熱變形誤差進行修正。于連棟[6]等提出了一種新型圓光柵測角誤差補償方法，基于諧波方法建立了含有環境溫度影響因子的圓光柵測角誤差補償模型，以提高關節臂式坐標測量機的測量精度。

綜上所述，目前對關節臂式坐標測量機熱誤差研究均是通過實驗的方法獲得溫度變化后的運動學參數，并研究運動學參數變化量與溫度的關系，尚缺乏數值模擬與理論上的支撐，溫度變化對關節臂式坐標測量機測量精度影響的機理還不夠明確。

為探明關節臂式坐標測量機熱變形規律及其對運動學參數的影響，本文建立了關節臂式坐標測量機的有限元分析模型，得到了熱變形分布圖，提出一種虛擬坐標測量方法，在有限元分析后測得關節臂式坐標測量機的運動學參數，并以此建立熱誤差模型，驗證了模型的正確性。

1 關節臂式坐標測量機建模與有限元分析

1.1 運動學建模

關節臂式坐標測量機是由連桿串聯多個關節組成的一種空間開鏈式機構。通常采用D-H（Denavit-Hartenberg）法來建立關節臂式坐標測量機的運動學模型[7]。運動學模型實現了關節臂式坐標測量機關節空間到坐標空間的變換，是關節臂式坐標測量機測量的數學基礎。

本文實驗對象如圖1 所示。關節臂的型號為ROMER RA-7125。根據D-H 法在各關節處建立了關節臂式坐標測量機的坐標系統，如圖2 所示。通過計算關節臂式坐標測量機兩個相鄰關節間的齊次變換矩陣Ti-1,i，見式（1），逐個相鄰關節變換矩陣連乘后再乘以測頭偏置（lx，ly，lz，1）T，見式（2），就可得到末端測頭中心在基坐標系下的坐標（x,y,z,1）T。

圖1 關節臂式坐標測量機Fig.1 Articulated arm coordinate measuring machine

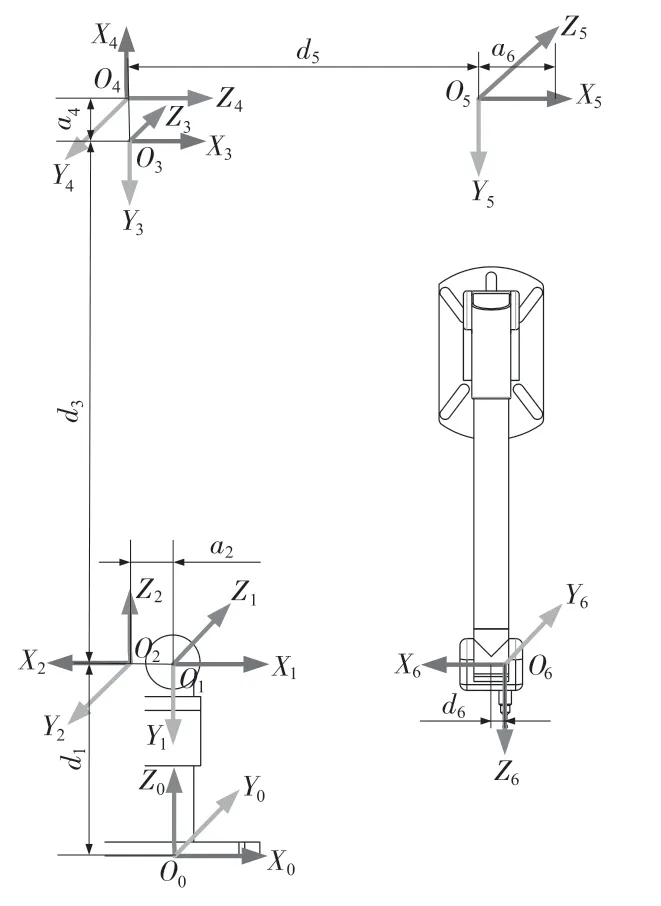
圖2 關節臂式坐標測量機的坐標系統圖Fig.2 Coordinate systems of articulated arm coordinate measuring machine

式中：i=1～6——關節序號；θi——關節轉角，為變量，其值可由安裝在軸端的編碼器測得；αi——關節扭轉角；di——連桿偏距；ai——桿長。

式中：lx，ly，lz——測頭中心在第6 關節坐標系中的位置。

1.2 關節臂式坐標測量機熱誤差有限元分析

關節臂式坐標測量機的工作溫度范圍通常為10～40 ℃，本文以25 ℃為參考基準，在10～40 ℃范圍內分析關節臂式坐標測量機各關節運動學參數隨環境溫度變化的規律。

相比實際關節臂式坐標測量機，對外置平衡機構、外殼、防護罩部分進行簡化，建立簡化的三維模型。這些零件對運動學參數的熱變形沒有影響，簡化的模型不影響熱誤差分析結果。關節臂式坐標測量機主要由2 種材料組成，關節處的零件主要為7075 鋁合金，連桿為碳纖維，相關屬性如表1 所示。關節臂式坐標測量機的運動學參數如表2 所示。

表1 關節臂式坐標測量機主要材料屬性Tab.1 Properties of main materials of articulated arm coordinate measuring machine

表2 運動學參數值Tab.2 Values of kinematic parameters

將關節臂式坐標測量機簡化三維模型導入有限元分析軟件，對模型的各部分材料進行設置。ANSYS 自動網格劃分的網格自適應能力較強，本文采用其自動網格劃分，網格大小也采用智能設置。固定關節臂式坐標測量機基座，并施加溫度載荷，分析施加溫度載荷后關節臂式坐標測量機的整體形變。

本文在3 種位姿下分析關節臂式坐標測量機熱變形情況。3 種位姿分別采取較近、適中、較遠位置，以此覆蓋關節臂式坐標測量機的主要工作空間。在關節臂式坐標測量機的工作溫度范圍10～40 ℃下每隔3 ℃采集一次數據做分析，由于40 ℃下關節臂式坐標測量機的熱變形誤差最大，所以選用40 ℃下3 個位姿的熱變形圖作為例子展示其熱變形情況，分別如圖3—圖5 所示。

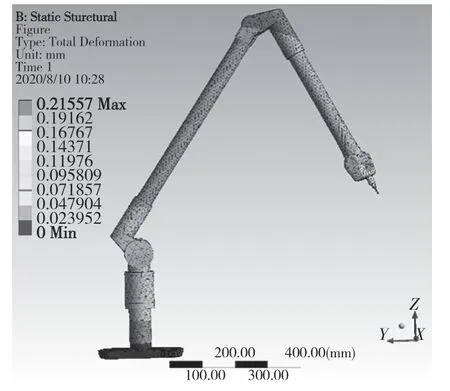
圖3 40 ℃下位姿一熱變形Fig.3 Thermal deformation of pose 1 at 40 ℃

圖4 40 ℃下位姿二熱變形Fig.4 Thermal deformation of pose 2 at 40 ℃

圖5 40 ℃下位姿三熱變形Fig.5 Thermal deformation of pose 3 at 40 ℃

由圖3—圖5 可以看到，隨著末端位置遠離基座，熱變形越大，熱變形隨著機構呈現逐級放大的情況[8-9]，在較遠位置的最大變形量為0.213 mm。

2 熱誤差補償建模與仿真驗證

2.1 關節空間參數虛擬測量及熱誤差補償模型建立

為量化熱誤差對關節臂式坐標測量機參數的影響，提出一種虛擬坐標測量方法。基于坐標測量原理提取有限元分析后的節點位置數據，利用點擬合線和面等幾何元素，再通過對擬合的幾何元素之間距離和夾角的計算，得到關節臂式坐標測量機的運動學參數。如圖6 所示，通過虛擬測量，發現關節臂式坐標測量機的角度參數θi，αi不變，而長度參數di，ai變化較明顯。

圖6 有限元節點提取及幾何元素擬合Fig.6 Extraction of finite element nodes and geometric element fitting

由于溫度變化對長度為0 的幾何參數不會產生影響，所以本文只對關節臂式坐標測量機中不為0 的長度量d1，d3，d5，d6，a2，a4，a6進行測量，分析溫度變化對它們的影響規律。經分析發現，關節臂式坐標測量機3 個位姿在同一溫度下的各參數的測量值基本一致，取3 個位姿測量的平均值。在不同溫度下測量得到的結果如表3 所示。可以看出，隨著溫度的升高，長度參數總體呈逐漸增加的趨勢。

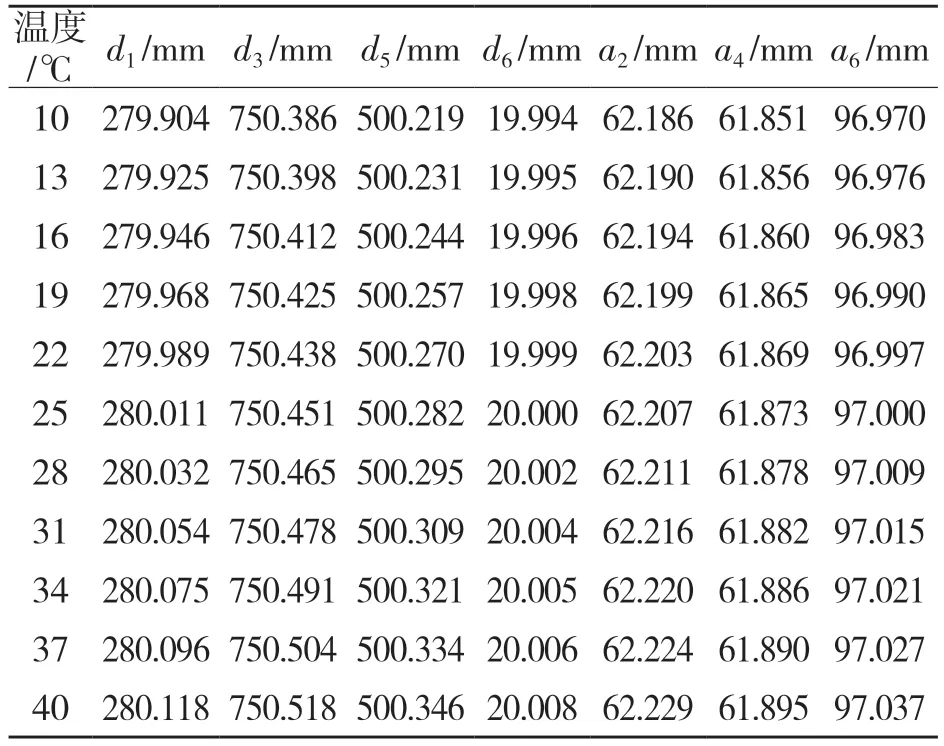
表3 各溫度下長度參數Tab.3 Length parameters at different temperatures

根據表3 中長度參數值的變化可發現，長度參數隨溫度升高呈近似線性增加的現象。由材料平均線膨脹系數計算式[10]對關節臂式坐標測量機6 個關節各用一個對應的溫度系數Ci來描述長度參數隨溫度變化的關系，如式（3）所示。根據虛擬測量的結果計算得到各關節的溫度系數如表4 所示。通過各關節溫度系數可以計算各關節在工作溫度范圍內任意溫度下的長度參數。

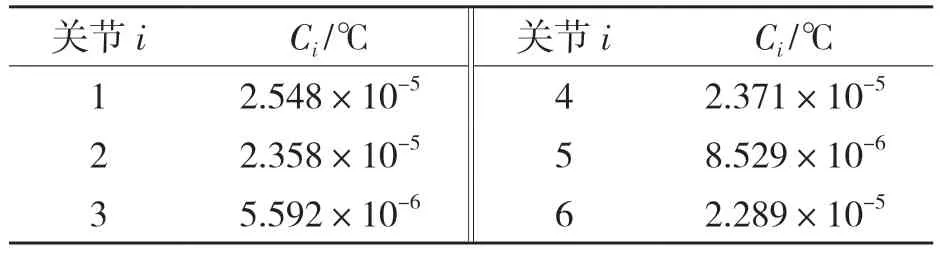
表4 各關節溫度系數Tab.4 Temperature coefficients of the joints

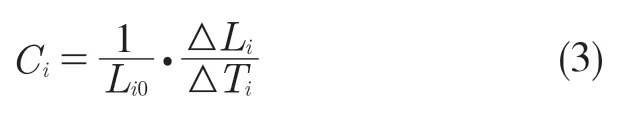
式中：L0——基準溫度下的長度；ΔL ——長度的變化量；ΔT——溫度的變化量；i=1～6——關節1～6。

由有限元分析后得到溫度系數Ci可計算關節臂式坐標測量機各關節在工作溫度范圍內任意溫度下的長度參數變化量，從而建立基于運動學參數的關節臂式坐標測量機熱誤差補償模型，如式（4）和式（5）。

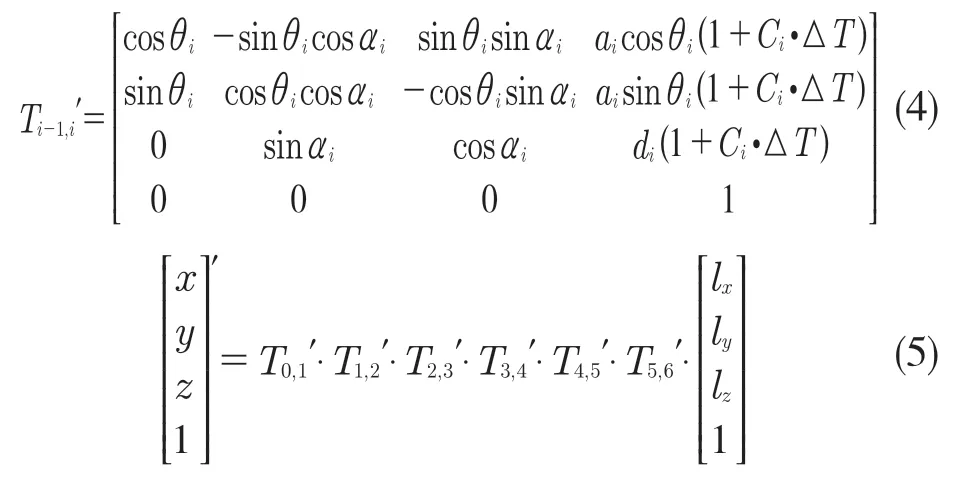
式中：i=1～6 ——關節1～6。

2.2 熱誤差仿真補償

使用式（5）中給出的誤差補償模型，對關節臂式坐標測量機熱誤差進行補償仿真。為了避免使用建立誤差補償模型時用過的溫度數據，分別在15，20，30，35 ℃下通過虛擬測量的方法采集數據并進行驗證。將25 ℃作為參考溫度，在此溫度下位姿一、二、三的測頭中心坐標分別為P1（-44.026，-705.601，448.854），P2（105.438，-1 186.060，230.614），P3（252.507，-812.426，356.097）。六自由度關節臂式坐標測量機是冗余機構，測頭中心保持在同一個位置時，可以通過改變各關節的轉角來改變其姿態。為了將姿態對測量結果的影響納入進來，在上述P1，P2，P3位置處，通過運動學逆解計算出每個位置的任意5 組關節轉角，將這些關節角代入式（5），可以分別計算出熱誤差補償前后15，20，30，35℃下的末端位置。對每個位置的5 組末端位置數據分別求其平均值作為該溫度下補償后的位置，3 個補償后的位置再計算相互之間的空間距離，通過在15，20，30，35 ℃下的仿真距離，分析與補償后的距離差值驗證空間距離精度提高的情況。圖7—圖9 分別為距離1、距離2、距離3在上述驗證組溫度下補償前后空間距離精度對比圖，熱誤差補償后3個空間距離精度分別從0.025，0.024，0.035 mm 提高到了0.008，0.012，0.014 mm，空間距離精度得到顯著提高。

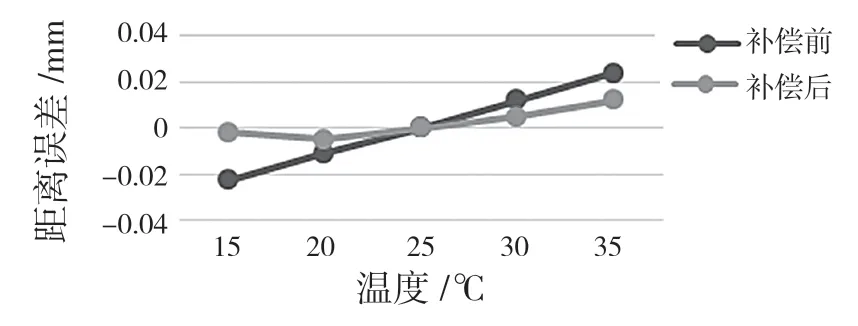
圖7 距離1 補償前后精度對比Fig.7 Accuracy comparison before and after compensation for distance 1

圖8 距離2 補償前后精度對比Fig.8 Accuracy comparison before and after compensation for distance 2

3 結論

對關節臂式坐標測量機的熱誤差進行有限元分析，得到了熱變形分布圖；提出一種虛擬坐標測量方法測得熱變形后的運動學參數隨溫度的變化規律，對每個關節提出一個溫度系數并建立相應的熱誤差補償模型，使關節臂式坐標測量機的精度及穩定性得到了極大的提高。

采用有限元分析手段及數值仿真技術對關節臂式坐標測量機熱誤差進行分析，彌補了目前缺乏數值模擬與理論支撐的缺陷；通過運動學參數的虛擬測量進一步明確了熱誤差對關節臂式坐標測量機精度的影響機理，對關節臂式坐標測量機后續的熱誤差分析提供了有效指導。