基于影響矩陣增設虛擬張拉工況優化施工索力的方法分析

■張 凱

（上海市市政公路工程檢測有限公司，上海 201108）

斜拉橋的斜拉索作為主梁的彈性支承使主梁彎矩減小，水平分相當于主梁的體外預應力，從而大大增加了斜拉橋的跨越能力，而且兼顧景觀功能使斜拉橋成為大跨徑橋梁的優先選擇[1]。 斜拉橋可以通過調整施工索力優化結構截面的內力、位移或應力等效應[2-6]，將拉索索力組成的列向量作為施調向量， 結構的效應組成的列向量作為受調向量，通過影響矩陣建立受調向量與施調向量之間的相關關系[7-8]。

Midas civil 可以通過“未知系數法[9]”和“調整索力”2 種功能進行調索，其原理都是基于影響矩陣法調整索力，“未知系數法”可以以某個施工階段的內力、位移和反力為控制目標，求出施工索力調整的“未知系數”， 最終施工索力=原初拉力×未知系數，以新求得最終施工索力正裝分析即可達到目標成橋狀態。 “未知系數法”不能以最直觀的應力為目標進行調整。 而“調整索力”功能可以以某個施工階段的內力、位移和應力為控制目標，一般適合于微調索力，其根據調整范圍進行搜索尋找調整值，調整范圍即為現在索力上下浮動的百分比，調整前很難掌握索力的調整范圍， 如果固定調整范圍的百分比，會造成原來索力大的調整幅度更大，原來索力小的索力變化很小，進一步增加了“搜索”滿足“約束條件”的困難。

本文提出一種基于Midas civil 的施工索力優化方法，以某斜拉橋為實例，使用影響矩陣法以主梁應力的可行域為目標，在實際張拉工況后增加虛擬索力張拉工況，使得成橋狀態主梁應力滿足預定要求，再使用“未知系數法”以主塔位移為目標微調索力，從而使主塔彎矩不會太大，最后手動微調索力最終達到索力分布均勻、 主梁應力在 “可行域”內，主塔彎矩不太大等合理成橋目標[10]。

1 工程概況

某斜拉橋主橋為雙塔雙索面結合梁斜拉橋，跨徑組合為54 m+114 m+400 m+114 m+54 m， 總長736 m，橋面寬29.2 m，橋面采用10 cm 瀝青混凝土鋪裝。 主塔采用寶瓶形橋塔，北塔高為123.52 m，南塔高為124.52 m。 主梁采用鋼—混凝土結合梁，由縱梁、橫梁、小縱梁等組成，縱梁與橫梁間、縱梁與小縱梁節段間采用栓接連接， 結合梁混凝土橋面板板厚26 cm。 預制混凝土橋面板采用C60 混凝土；后澆筑接縫采用低收縮C60 混凝土，主橋的主體結構鋼材采用Q345qD 鋼。 斜拉索采用扭絞型平行鋼絲斜拉索，空間扇形雙索面布置，全橋共84 對斜拉索。 主橋輔助墩為分離式矩形空心墩。 主塔上支座為2 個雙向活動支座，主梁與主塔間設置橫向抗風支座，輔助墩支座為2 個單向活動支座， 邊墩支座為1 個單向活動支座和1 個雙向活動支座，支座布置圖見圖1。

圖1 支座布置圖

橋梁施工流程：基礎施工→主塔及邊墩輔助墩施工→L0#、LZ1#、LB1# 梁段支架搭設→安裝L0#、LZ1#、LB1# 鋼梁并掛索→設置塔梁臨時固結→拼裝橋面吊機→支架安裝LB2#～LB21# 節段并安裝橋面板→安裝LZ2# 標準梁段、Z2# 與B2# 掛索（橋面吊機整體吊裝）→Z2# 與B2# 斜拉索初張→安裝LZ2# 橋面板→Z2# 與B2 斜拉索二張→澆筑LZ2#與LB2# 濕接縫→Z2# 與B2# 斜拉索三張……依此類推施工LZ3#～LZ21#節段（邊跨同上）……→安裝主跨合龍梁段（提前搭設梁段支架）→安裝主跨合龍梁段橋面板→澆筑主跨合龍梁段濕接縫→拆除橋面吊機→預應力張拉→二期恒載鋪裝→全橋調索→成橋。 圖2、圖3 為主梁節段劃分圖。

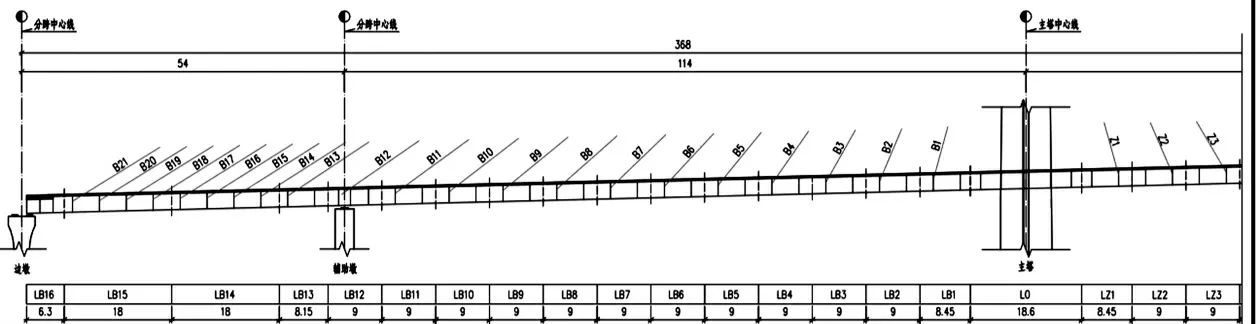
圖2 主梁節段劃分（一）

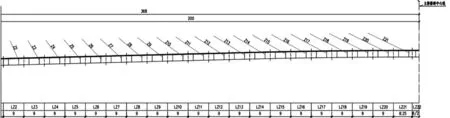
圖3 主梁節段劃分（二）

2 施工索力優化

2.1 有限元模型的建立

采用有限元軟件Midas civil 建立該橋施工階段正裝模型。 主塔用梁單元模擬，主梁為疊合梁，主梁疊合梁的鋼梁和橋面板分別用梁單元模擬，采用共節點法將橋面板和鋼主梁耦合在一起，并在截面屬性中修改偏移量從而避免了設置橋面板和鋼梁之間的剛臂。 拉索采用索單元模擬，線性分析時，索單元按等效桁架單元進行分析；在幾何非線性分析時，索單元按彈性懸鏈線索單元進行分析。 使用影響矩陣法前提是不考慮幾何非線性，按等效桁架單元進行分析時，索單元根據恩斯特公式在分析時計入索垂度效應。

2.2 成橋目標可行域

本文選擇主梁橋面板和鋼梁的上下緣應力作為控制目標。 為保證在最不利狀況下主梁應力都不超過規范規定的允許值，主梁的恒載應力大小應控制在一定的范圍內（這個范圍即為“可行域”）。 根據規范規定，混凝土的法向壓應力應符合：

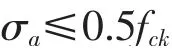
影響主梁正應力的荷載因素一般為永久作用和可變作用兩大部分，根據規范可得：

式中σ—成橋狀態主梁截面應力； σd—成橋狀態主梁截面各項永久作用產生應力總和；σl—成橋狀態主梁截面各項可變作用產生應力總和；σa—主梁容許應力。

由（1）式可得

而成橋狀態主梁截面可變作用應力也在一定的范圍內，即σlmin≤σl≤σlmax，故

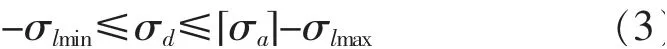
不等式（3）分別是主梁應力的上下限，其之間區域就是成橋狀態下主梁截面恒載應力的可行域。

根據設計，橋面板混凝土的主梁壓應力容許應力為[σa]=0.5×（-38.5 MPa）=-19.25 MPa，圖4 所示活載作用下橋面板應力范圍為-4.35～3.39 MPa，根據上文計算各橋面板單元成橋使用階段恒載作用下的應力可行域為-14.90～-3.39 MPa； 圖5 所示活載作用下鋼梁底部應力范圍為-60.10～66.69 MPa，取鋼梁容許應力[σa]=0.7×（±345 MPa）=±241.5 MPa，根據上文計算各橋鋼梁單元成橋使用階段恒載作用下的應力可行域為-174.81～154.40 MPa。

圖4 活載作用下橋面板應力包絡圖

圖5 活載作用下鋼梁底部應力包絡圖

2.3 影響矩陣法優化施工索力

斜拉橋施工過程中的初張拉索力主要平衡當前施工階段的自重或施工荷載，如圖6 所示，掛鋼梁索力和安裝橋面板后二次張拉力按索力豎向分力與節段當前豎向力平衡確定，澆筑濕接縫后鋼梁與橋面板共同工作，施工階段每根索最后張拉力即澆筑濕接縫后第三次張拉力初步擬定為設計成橋狀態索力，然后根據分析結果對第三次張拉力進行優化。

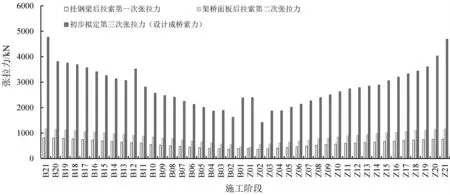
圖6 施工階段拉索初拉力

按施工順序建立正裝分析模型，施工工況中每個張拉工況邊跨拉索和中跨拉索是同時張拉的，給使用影響矩陣法分別調整邊跨索力和中跨索力帶來了不便。 Midas civil“調整索力”功能中的“搜索”功能，根據索力“調索前”索力的大小和“調索范圍”計算“開始值”和“結束值”，如圖7 所示，“調索前”索力為1000，“調索范圍”為20%，則索力調整范圍就是在1000 的基礎上上下浮動20%，則“開始值”是800，“結束值”是1200，在800～1200 之間尋找接近目標值的“調索后”索力。 為了尋找目標函數收斂的解，“搜索”功能需要反復執行，直到“調索前”和“調索后”中的計算結果不再變化。 因各拉索“調整前”索力不同，調整范圍難以把握，若為同一調整范圍，如“調整范圍”均為20%，“調索前”索力大的變化范圍更大，索力小的變化范圍更小，有時候更難找到需要的優化索力。 為了便于調索，在每個節段第三次拉索張拉完畢后新增2 個虛擬張拉工況，分別為該節段單獨張拉邊跨拉索和中跨拉索的虛擬工況，最終施工索力即為原澆筑濕接縫后第三次拉索張拉力與虛擬張拉工況索力值之和。 新增張拉虛擬工況張拉力為1 kN，同時也方便后期使用“未知系數法”調索。 通過調節新增虛擬張拉索力工況的索力使成橋狀態達到目標狀態，避免了“調索前”索力大的拉索調整范圍更大、“調索前”索力小的調整范圍反而更小的情況出現，使每根拉索的調整范圍都在同一“起跑線”上，降低了對“調索前”索力值的敏感性[11]。

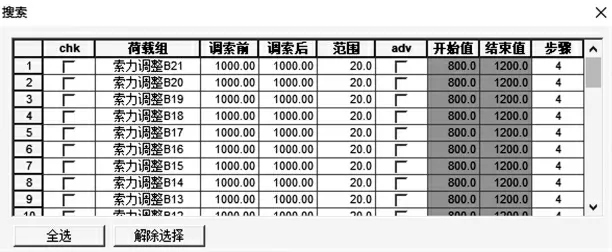
圖7 Midas civil“調索功能”

Midas civil 調整索力功能可以查看“施調量”與“目標量”之間的影響矩陣，通過查看影響矩陣找出對目標值較敏感的“施調量”，即虛擬張拉工況的索力值，利用“調整索力”功能中的“搜索”功能調節虛擬張拉力， 初步滿足應力可行域的約束條件。 表1為虛擬張拉工況索力值與最終成橋索力值之間部分影響矩陣。 因索單元不能輸入壓力即負值，有的拉索虛擬張拉工況索力值計算值為負值，將初步擬定索力與上一步求出的虛擬張拉工況索力疊加后作為每個節段新的第三次張拉力，其后仍然保留虛擬張拉工況以備后續調整索力使用，虛擬張拉工況索力索力改為原來的1 kN，進行正裝分析。使用“未知系數法”調節主塔位移，虛擬張拉工況索力作為未知量，主塔位移作為約束條件，求出未知系數，虛擬張拉工況索力值即為未知系數×單位力； 同樣按第二步的方法將所求得的虛擬張拉力與第三次張拉力疊加作為每個節段新的第三次張拉力，其后仍然保留虛擬張拉工況以備后續調整索力使用，虛擬張拉工況索力改為原來的1 kN，繼續進行正裝分析。再次使用影響矩陣法微調虛擬張拉力，使用“調整索力”功能手動微調使得索力分布均勻、主梁應力仍然在“可行域”內。 求出的虛擬張拉工況的張拉力，再次與上步所得第三次張拉力進行疊加，作為每個節段新的第三次張拉力，進行正裝分析，該張拉力即為最終優化后施工索力。

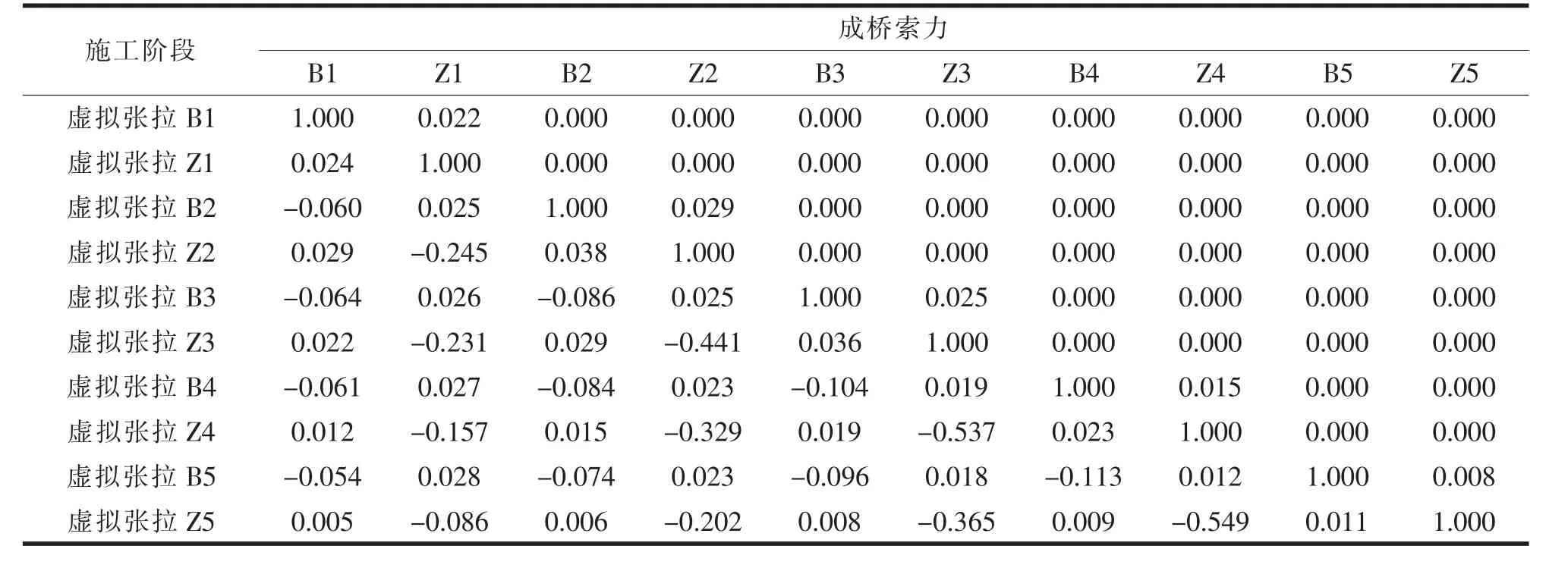
表1 調整索力與成橋狀態索力對應的部分影響矩陣

表2 為按照以上方法優化后的施工索力，即施工過程中澆筑濕接縫后每根拉索最終的施工張拉力。 按優化后的施工索力正裝分析成橋索力分布均勻。

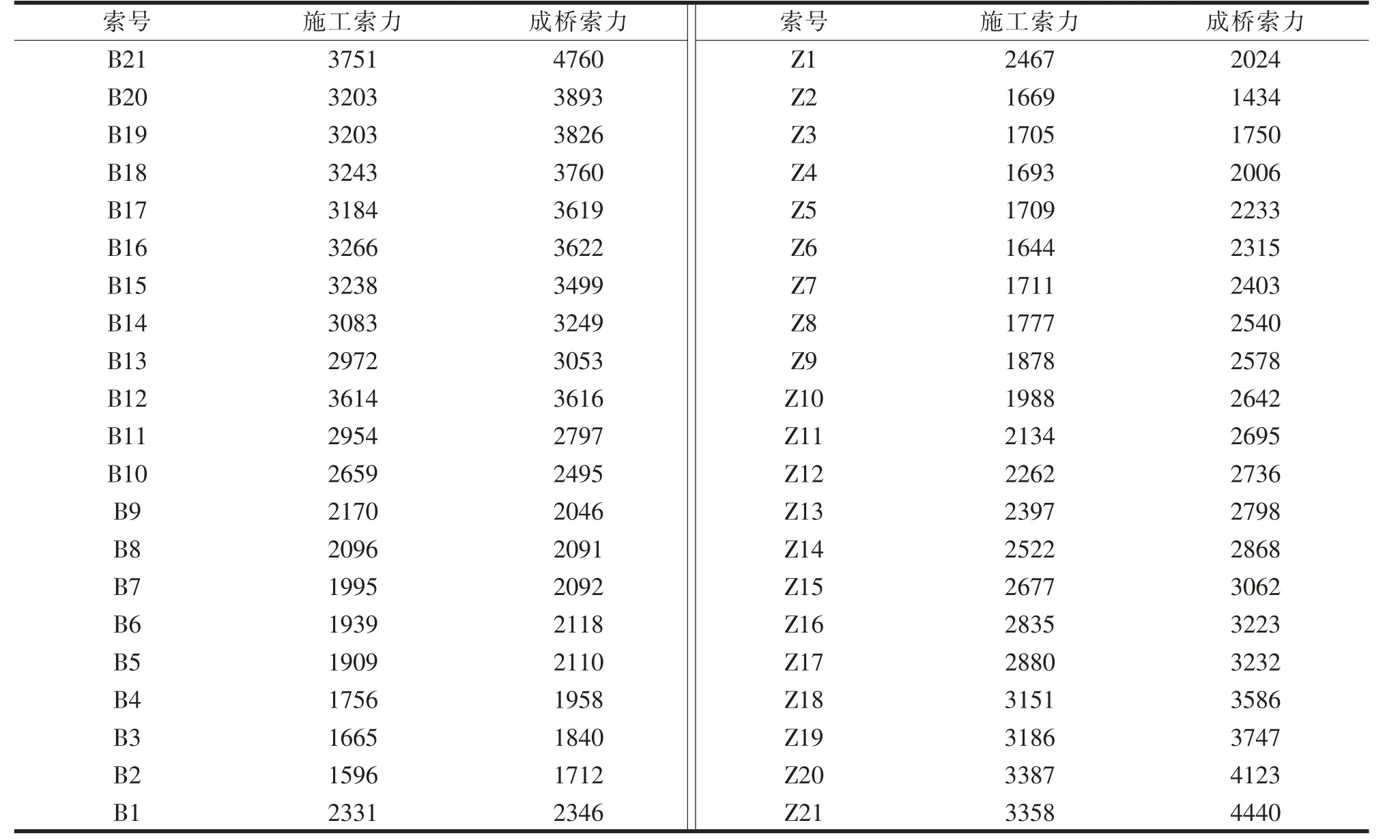
表2 優化后施工索力與成橋狀態索力 （單位：kN）

圖8 為按最終優化施工索力正裝分析后成橋狀態下橋面板最大應力圖和拉索索力圖，優化施工索力后成橋狀態橋面板壓應力為-9.6～-3.1 MPa，滿足橋面板應力可行域為-14.9～-3.39 MPa 的要求。圖9、圖10 為按最終優化施工索力正裝分析后成橋狀態鋼主梁上、下翼緣應力圖，鋼主梁應力為-141.2～43.7 MPa，滿足應力可行域為-174.81～154.40 MPa的目標要求。 圖11 為成橋狀態彎矩分布圖，主塔彎矩不大。 通過優化施工索力后成橋索力分布均勻，主梁橋面板和鋼梁應力均在“可行域”內，索力分布均勻，主塔彎矩不大，通過優化施工索力達到了成橋狀態合理的目標。

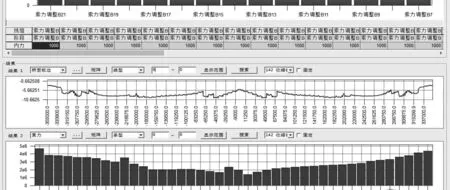
圖8 索力優化后成橋狀態主梁應力和拉索索力

圖9 成橋狀態主梁鋼梁上翼緣應力

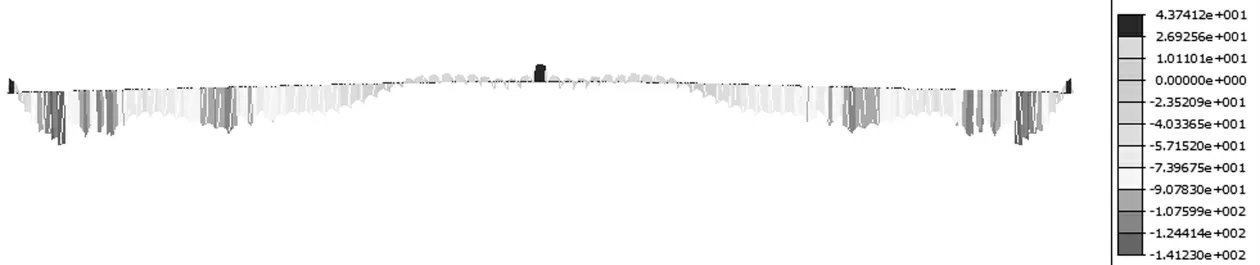
圖10 成橋狀態主梁鋼梁下翼緣應力

圖11 優化后成橋彎矩

3 結論

基于影響矩陣法使用Midas civil 有限元軟件進行施工索力優化分析，為了能在Midas civil 軟件中分別以混凝土橋面板和鋼梁的應力可行域為目標進行優化施工索力， 分別建立橋面板和鋼梁單元， 采用共節點法將橋面板與鋼梁耦合在一起，操作簡單方便。 用索單元模擬拉索，在線性分析中考慮了拉索的垂度效應，使計算精度更高。 Midas civil的“調整索力”功能一般適合微調，“未知系數法”適合大幅度調整，“調整索力”功能可以以應力為調整目標，但“未知系數法”只能以內力和位移作為“約束條件”，不能以應力為目標進行調整。 本文提出在施工階段每根拉索張拉完畢后新增相應拉索的虛擬索力張拉工況，最終施工索力為每根拉索原施工張拉力與新增虛擬張拉工況索力之和。 只調整虛擬張拉工況索力值克服了“調整索力”功能調整前索力大的拉索調整范圍大、索力小的拉索調整范圍小的缺點，使該方法更具有實用性和優越性。