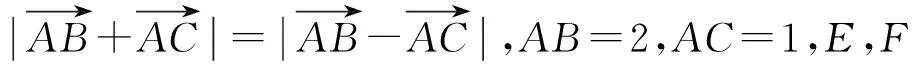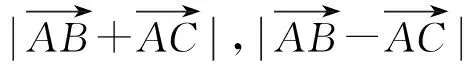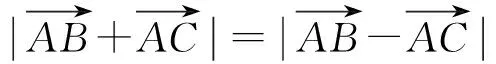高中數學課堂教學中落實直觀想象素養培養的設計
201600 上海市松江一中 曹素玲
伴隨著新一輪課程改革的推進及新教材的實施,如何落實數學核心素養,提高課堂教學效率成為廣大教師面臨和亟需解決的問題.與此同時,課堂教學作為落實教育教學的“主戰場”,便自然而然地成為培養學生核心素養的主要陣地.直觀想象素養作為數學六大核心素養之一,是學生數學學習過程中必不可少的一種基本素養,它是指借助幾何直觀和空間想象感知事物的形態與變化,利用空間形式特別是圖形理解和解決數學問題的素養.筆者結合具體實例,闡述直觀想象素養在高中數學課堂教學中的培養.
一、 注重教學情境的創設,激發學生學習的興趣
在教學中要合理創設直觀情境,其中包括實際情境、科學情境、數學情境、歷史情境等.合理創設情境便于學生理解學習內容和要完成的任務,能夠激發學生的興趣和熱情,也有利于提高學生應用數學的能力.例如,對于“函數的單調性”一節的引入環節進行如下設計.
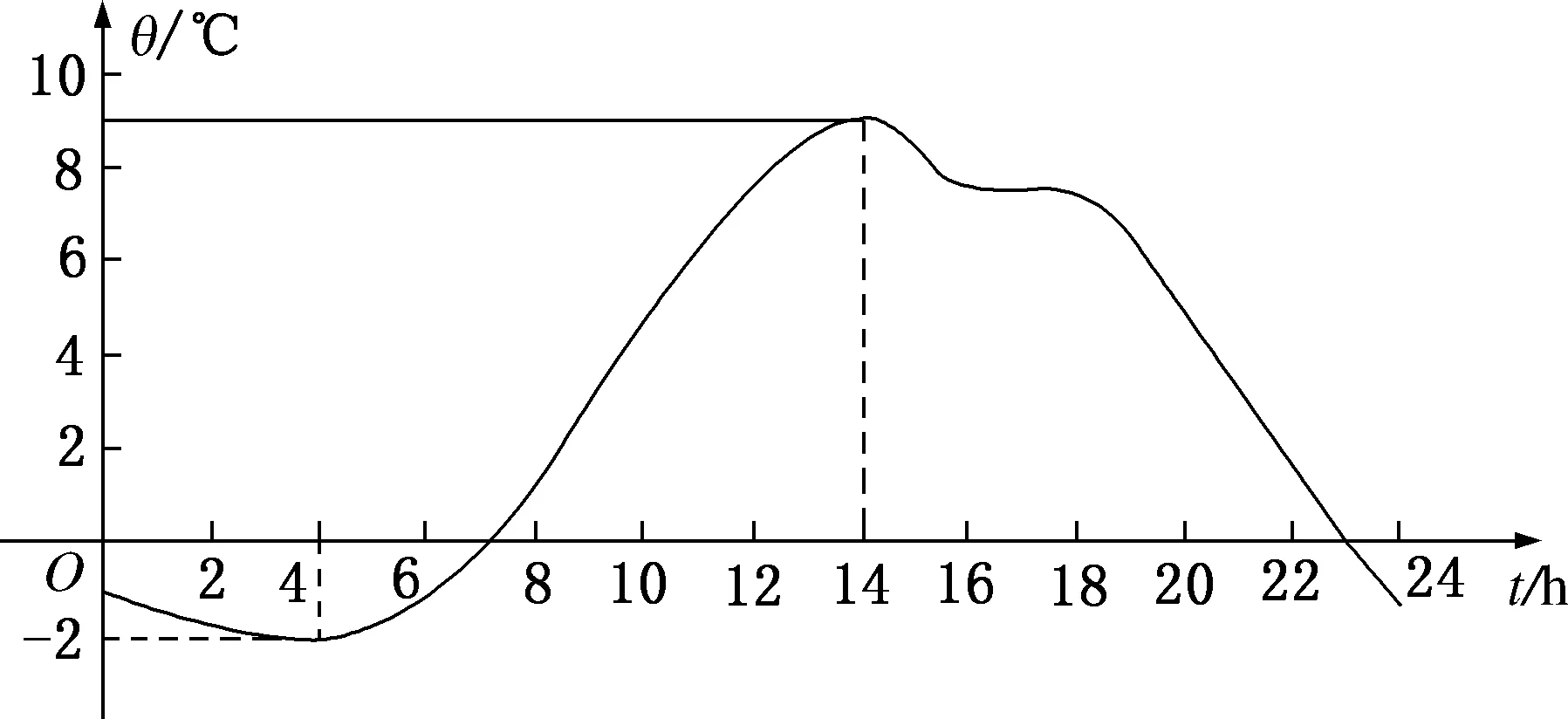
情境1回顧我們之前學習過的指數函數與對數函數的圖像,分別說說當a>1和0 指數函數圖像如表1所示. 表1 對數函數圖像如表2所示. 表2 設計意圖:新教材對函數的編排做了很大的調整,將指數函數和對數函數提到函數的概念之前,體現了由特殊到一般的思想,順應學生的認知發展規律,便于學生由具體函數直觀地認識函數的性質.本節課從學生熟悉的指數函數、對數函數圖像入手創設情境,讓學生直觀感受圖像中“當a>1時,y隨x的增大而增大”和“當0 情境2氣溫曲線 你注意過一天之內的氣溫變化嗎?請根據我市某日氣溫隨時間變化的曲線圖(如圖1所示),說說氣溫的變化情況. 圖1 設計意圖:氣溫波動是學生在現實生活中能夠切實感受到的,借助學生實際生活的感受經驗引入,讓學生感受氣溫在某個時間段“上升”“下降”的趨勢與圖像單調性的聯系,初步獲得對函數單調性的感性認識,為理性概念的生成做鋪墊. 理解函數單調性的形式定義僅僅是理解函數性質的一部分,在教學中,教師也要培養學生的模型意識,使學生在頭腦中“留住”一批具體的函數模型,這樣不僅可以幫助學生提升直觀想象素養,還可以對輔助函數性質的教學起到事半功倍的效果. 從平面幾何過渡到立體幾何時,思維方式會發生較大的變化.從以往學生的數學學習經驗來看,很多學生不具備從二維空間迅速切換到三維空間的能力,尤其對于空間想象能力欠發達的學生來說,他們遇到的困難更大.因此,教師在進行立體幾何教學時,可引導學生親手制作立體幾何模型,通過觀察現實模型,恰當運用類比思想,不斷培養、發展和完善學生的直觀素養.例如,讓學生動手制作圓錐模型,觀察從圓錐側面沿母線剪開得到的展開圖是扇形,在此基礎上,教師再啟發引導學生尋找平面幾何與立體幾何之間的關系,發現扇形弧長與底面圓周長相等,從而掌握二者間的轉化.除了制作模型,教師還要引導學生通過對模型的理解與洞察將問題直觀化.例如,在講解“多面體的表面積”時,筆者布置了一道2005年的高考題作為拓展題. (1)用它們能拼成什么樣的幾何體? (2)在所有可能拼成的直四棱柱情形中,全面積最小的是哪一個?全面積是多少? (3)在所有的情形中,全面積最小的是一個四棱柱,求a的取值范圍. 設計意圖:模型是想象的基礎,通過利用模型,學生可以更容易地理解和推理數學問題,本題主要考查棱柱的側面積和表面積,學生通過動手制作模型,拼接模型,很快就會發現這兩個直三棱柱可以拼成一個直三棱柱和三個直四棱柱,接著根據公式分別求出棱柱的側面積和表面積,通過比較,問題就迎刃而解了.空間想象能力的培養不是一蹴而就的,在學習立體幾何之初,教師一定要多注重實物模型演示,讓學生多運用直觀感知、操作確認、度量計算等認識和探索空間圖形的性質,逐步發展空間想象能力,培養直觀想象素養. 圖2 方法1:先伸縮后平移(如圖3-1所示). 方法2:先平移后伸縮(如圖3-2所示). 圖3-1 圖3-2 設計意圖:函數y=Asin(ωx+φ)的圖像與性質是三角函數中的一個較為抽象的內容,在較為抽象的數學知識的教學過程中,應該充分利用多媒體技術,形象地揭示知識的產生或變化過程,在動態的分析探究中深化對概念的認知,促進學生直觀表象能力的形成. 直觀想象是學生發現和提出數學問題,分析和解決數學問題的重要手段,是探索和形成論證思路、進行邏輯推理、構建抽象結構的思維基礎.直觀想象素養的培養不是一朝一夕能夠完成的,它需要教師在教學過程中不斷引導學生深入挖掘題目的條件,發現條件背后隱藏的數學思想方法,并盡可能幫助學生形成一些有用的“數學模型”.學生遇到新問題時,能對問題直觀地進行判斷,甚至無需論證推理就能直接看出一些結論,然后再運用相關結論解決問題.筆者在向量的習題課中選取了這樣一道例題. 圖4 設計意圖:知識的積累依賴于直觀,數形結合思想正是數學核心素養中“直觀想象”的體現.在處理本題時,正因為抓住了“公共始點”“和”“差”“模”“數量積”等關鍵詞,把向量問題轉化成三角形或四邊形中的“距離”問題,才達到了數形轉化的目的.在教學中,要增強學生運用“直觀想象”思考問題的意識,提高學生數學素養. 直觀想象素養的培養不是在短時間內就能完成的,它需要依托具體的數學知識與方法,在數學知識的學習、數學思想方法的掌握過程中,通過逐步積累、領悟、內省形成.對于絕大多數學生來說,數學能力的形成與數學核心素養的提升主要依賴于(或源于)數學課堂,因此,在結合新教材備課的過程中,教師要多思考教材編寫者的意圖是什么,教師應該向學生教什么,怎么教,這樣才能使直觀想象素養的培養得到有效體現與落實.

二、 注重實物模型的制作,增進直觀想象素養的發展
三、 注重多媒體技術的運用,促進直觀表象能力的形成
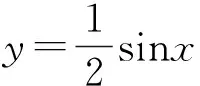
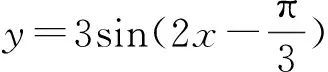

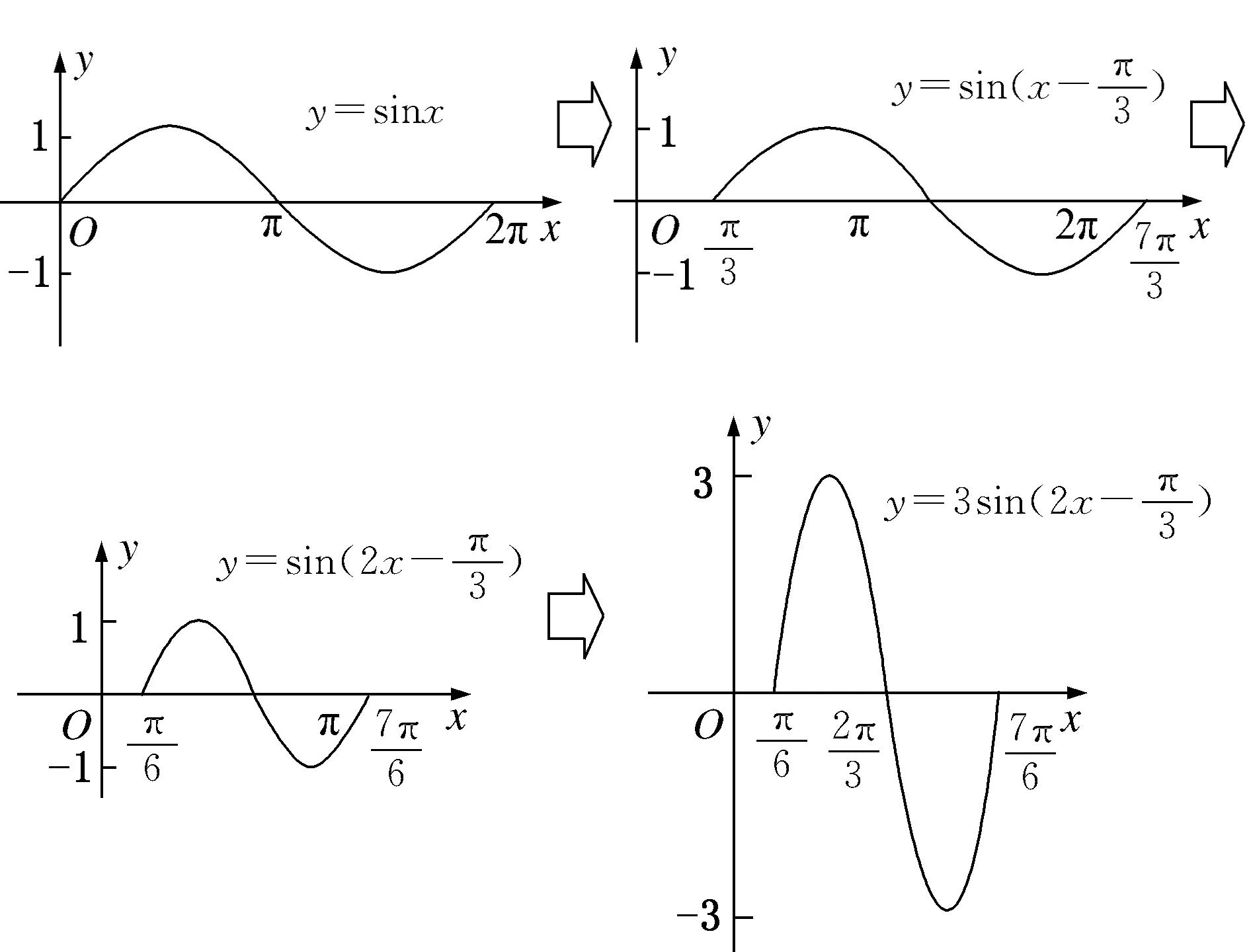
四、 注重數形結合的滲透,促進直觀素養的提升