基于二階元分析的教育游戲對學生學習效果的影響研究*

趙篤慶 沈 超 余 亮

基于二階元分析的教育游戲對學生學習效果的影響研究*

趙篤慶 沈 超 余 亮[通訊作者]

（西南大學 教育學部，重慶 400715）

教育游戲作為一種支持學生學習和提升學生學習績效的重要手段，其有效性長期以來受到研究者和教師的廣泛關注。以往關于教育游戲對學生學習效果影響的元分析研究通常是基于一階元分析，但其存在一定的抽樣誤差，且容易受到發表偏倚影響，致使研究結論的可信度受到質疑。相對于一階元分析，二階元分析在更大范圍整合實證研究，能夠進一步提升研究結果的準確度。基于此，文章首先梳理了教育游戲對學生學習效果影響的一階元分析研究，并闡述了二階元分析的基本原理；然后使用二階元分析定量綜合分析了11篇一階元分析文獻，探索教育游戲對學生學習效果的整體影響及其調節因素；最后基于研究結果，對教育游戲的設計與應用提出了建議，并總結了二階元分析的優勢和局限，以期為教育游戲和元分析研究發展提供參考。

二階元分析；教育游戲；學習效果；二階抽樣誤差

引言

教育游戲是教育和游戲相互融合的產物，是為了支持學生學習而專門設計的數字游戲。近年來，隨著信息技術的發展和教學理念的更新，研究者充分認識到了教育游戲提升學生學習績效的潛力，關于教育游戲的實證研究和教學應用逐年遞增[1]。在此背景下，教育游戲的有效性成為教育研究者和學校教師關注的重點之一。元分析是對某一研究領域內多項研究結果的定量綜合，是一種系統分析與評價整體研究情況的統計分析方法[2]。通過整合研究主題相近的實證研究結果，元分析研究可以精確地計算合并效應量，歸納多項實證研究反映的共同效應，并在一定程度上降低抽樣誤差的影響，得到較為綜合、準確的研究結論，從而證明某項干預措施的有效性。教育游戲領域內的元分析研究可以追溯到1981年[3]，在此之后，相近主題的元分析研究數量迅速增加。然而，盡管當前已經出現大量關于教育游戲有效性的元分析研究，且幾乎都表明教育游戲對學生學習效果具有提升作用，但在研究結論上仍存在一定爭議。這些爭議一方面來自數據分析結果的差異，即研究者對教育游戲能在多大程度上提升學生的學習效果尚未達成共識，不同元分析研究的調節效應分析結果存在分歧甚至相互矛盾；另一方面源于對元分析方法的質疑，即由于元分析研究的樣本總數有限，始終存在一定的抽樣誤差，使元分析研究結果不可避免地存在偏差，且容易受到發表偏倚影響，因此元分析研究結論的準確性有待商榷[4]。

為了盡可能減少抽樣誤差對研究結果的影響，彌合不同元分析研究結果之間的差異，獲得更全面、可靠的研究結論，有研究者提出可對已有相似主題的元分析研究再次進行元分析，以降低研究樣本中的二階抽樣誤差（Second-Order Sampling Error，即元分析研究樣本中存在的抽樣誤差，是指整合多項實證研究，消除一定抽樣誤差后剩余的抽樣誤差），這種分析方法被稱為二階元分析（Second-Order Meta-Analysis）[5]。與一階元分析（為區分傳統意義的元分析與二階元分析，使用一階元分析來表述此概念）相比，二階元分析能夠定量綜合分析已有元分析研究的結果，實現在更大范圍內整合實證研究結果，形成建立在更大樣本基礎上的可靠結論。當前，二階元分析已經應用于檢驗翻轉課堂的有效性和在線學習對學生學習效果的影響等研究[6][7]，這些研究證明了在教育領域中應用二階元分析的可行性。在教育游戲領域，雖然研究者借助一階元分析得到了一些有價值的研究結論，但其尚不能說明教育游戲對學生學習效果的整體影響。因此，本研究嘗試通過二階元分析探索教育游戲對學生學習效果的整體影響及其調節因素，以期形成對教育游戲有效性的更準確認識，為教育游戲和元分析研究發展提供參考。

一 研究現狀及問題提出

1 教育游戲對學生學習效果影響的一階元分析研究

梳理相關一階元分析文獻后，本研究發現雖然絕大多數研究表明教育游戲正向影響學生的學習效果，但對于其影響程度，研究者尚未達成共識。早期一些研究者發現教育游戲對學生學習效果的影響較小[8]，而近幾年越來越多的研究結果表明，教育游戲對學生學習效果的影響能夠達到中等程度甚至較大程度[9][10]，這似乎能夠說明教育游戲的有效性隨著時間的推移不斷提升。然而，在2019年發表的兩項一階元分析研究中，Tokac等[11]發現教育游戲對學生學業成就的影響極小，合并效應量只有0.13，遠低于其他研究者發現的影響效應；Riopel等[12]也發現教育游戲對學生學習效果只有較小程度的正向影響，合并效應量為0.31——這與前文提出的關于時間作用的研究推斷相矛盾。由此可以看出，不同一階元分析研究得到的合并效應量存在較大差異，當前尚未形成對教育游戲有效性的綜合判斷。另外，盡管大量研究先后檢驗了不同變量的調節效應，但得到的研究結論相互矛盾甚至截然相反。以學科為例，段春雨[13]提出教育游戲在科學中的應用效果優于數學，與之相反，李玉斌等[14]發現教育游戲在數學中的應用效果優于科學，說明兩者在對學科調節作用的認識上存在一定分歧，而諸如此類的分歧在當前的一階元分析研究結果中相對常見。上述現象的產生，可能是由一階元分析研究樣本覆蓋范圍有限造成的，也可能受研究視角和文獻篩選標準影響。從抽樣的角度來說，上述推斷可以概括為一階元分析研究結果的差異源于一階元分析研究樣本中存在的二階抽樣誤差，而二階抽樣誤差又會直接影響研究結論的準確性和可信度[15]。因此，基于“尋找最佳證據”的立場考慮，需要進一步整合這些一階元分析研究結果，減少二階抽樣誤差的不利影響，以形成對教育游戲有效性的準確認識。

2 二階元分析

二階元分析也稱“元—元分析”或“元分析的元分析”，是對某一領域內相似主題一階元分析研究的定量綜合，是對多項一階元分析研究結果的元分析。它通過計算不同一階元分析研究合并效應量差異的可信度，來估算各一階元分析研究的真實合并效應量，并降低二階抽樣誤差對合并效應量的影響[16]。相較于一階元分析，二階元分析有以下優點：①通過整合不同一階元分析研究結果，可以生成建立在更大樣本量基礎上的可靠結論；②能夠比較不同一階元分析研究之間的差異，檢驗各一階元分析研究結果的信效度[17]；③可以利用一階元分析研究的異質性，來檢驗更多調節變量（如出版信息、研究質量等）的影響[18]；④能夠彌補一階元分析研究的不足，如未解釋效應量獨立性影響、消除的發表偏倚有限等[19]；⑤研究成本相對較低（包括樣本搜集的時間、經費等），并能夠大范圍總結現有研究的整體情況，說明未來研究的發展趨勢[20]。

效應量是二階元分析的主要關注對象，它是衡量影響效應強度或變量關聯強度的統計量。根據效應量的統計學意義，可將其劃分為組間差異類效應量、相關類效應量和組重疊效應量[21]。Steenbergen-Hu等[22]提出，二階元分析中的組間差異類效應量計算分為三步：①從一階元分析研究中提取合并效應量；②將合并效應量統一轉化為Hedges’s g；③整合各一階元分析研究的合并效應量，經加權處理后得到Hedges’s g均值，該方法目前在二階元分析研究中常用。另外，相較于小樣本，大樣本合并效應量的可信度往往更優，標準誤更小。因此，許多研究者提倡選取包含實證研究樣本數較多的一階元分析研究作為研究對象以保障二階元分析的研究質量[23]。

統計獨立性是開展二階元分析的重要前提，它意味著應盡可能地避免不同一階元分析研究中的樣本信息重疊。盡管當前已經出現一些控制樣本信息重疊比例的方法，但并不能確定哪種方法是最佳處理方式。一些研究提出，可以通過剔除樣本信息高度重疊的一階元分析研究[24]，或只選擇研究方法最嚴謹、最新發表的一階元分析研究作為研究對象來保障統計獨立性[25]。然而，上述處理方法往往受到其他研究者質疑，因為納入樣本信息重疊的一階元分析研究能夠檢驗不同調節變量的影響[26]。一些研究發現，違背統計獨立性原則幾乎不會影響研究結果，在此基礎上有研究者提出可以選擇忽略樣本信息重疊問題[27]。然而，該觀點并未得到廣泛認同，很多研究者認為統計獨立性對二階元分析研究結果的影響程度尚不明確，需要進一步檢驗[28]。Wilson等[29]提出，由于無法完全消除一階元分析研究中存在的樣本信息重疊問題，因此將每項一階元分析研究的樣本重疊比例控制在25%以內并盡可能最小化即可接受，如果重疊比例大于25%，則需要有選擇地刪除相似一階元分析研究，目前該觀點被較多研究者采納。除此之外，開展二階元分析研究往往還需要考慮發表偏倚情況的影響。理想狀態下，二階元分析的研究對象應具有較高的研究質量和透明度，并且沒有發表偏倚，否則需要研究者做出相應調整[30]。

綜上，本研究提出“教育游戲對學生學習效果的整體影響如何？”“哪些因素會調節教育游戲對學生學習效果的影響？”兩個研究問題，并通過二階元分析予以回答。

二 研究設計

1 文獻檢索

本研究以中國知網、ProQuest、Science Direct等數據庫作為文獻來源，選取2002年1月～2022年2月發表的相關文獻作為研究對象，檢索時間截至2022年2月3日。中文文獻檢索標題為“元分析”“系統評價”“綜述”，關鍵詞為“教育游戲”“數字游戲”“嚴肅游戲”，并含“學習效果”“學習成績”“學業成就”。外文文獻檢索標題為“review”“meta-analytic”“meta-analysis”，主題詞為“educational game”“serious game”“digital game”，并含“learning outcome”“learning achievement”“academic performance”。另外，本研究還通過參考文獻回溯、專家咨詢等方式納入未發表的“灰色文獻”。完成檢索后，歸納并剔除重復文獻，最終得到131篇一階元分析文獻。

2 樣本篩選

本研究對得到的文獻進行篩選，標準如下：①文獻中的教育游戲指的是計算機游戲或數字游戲；②研究主題為教育游戲對學生學習效果的影響，需比較使用教育游戲和不使用教育游戲對學生學習效果的影響；③研究方法為元分析；④包含完整的數據信息，如樣本量、效應量、標準誤等；⑤研究對象是在校學生；⑥出版語言為中文或英文。按照標準篩選后，本研究提取并對比了所有一階元分析文獻包含的實證研究信息。為保證統計獨立性，本研究剔除了2篇樣本信息重疊率超過25%的文獻，最終剩下11篇一階元分析文獻（包含14個效應量），樣本信息重疊率為7.95%。如果完全排除實證研究重復項，則研究樣本包含1984年～2020年間開展的336項實證研究，參與者人數為36948人。

3 特征值編碼

接下來，本研究對文獻的特征值編碼，以便于后續統計分析和效應量計算工作的開展。本研究根據出版情況，將作者姓名、出版年份和來源按照實際情況錄入，將語言編碼為中文和英文；根據文獻信息，將學科按照原始類別錄入（如果包含多個學科，則編碼為綜合類），效應量類型編碼為Cohen’s d和Hedges’s g，樣本量和效應量按原始數值錄入，發表偏倚情況編碼為有偏倚、無偏倚和未說明。另外，標準誤分兩種情況編碼：如果原文提供標準誤，則按原始數值錄入；如果原文中未提供標準誤，則通過95%置信區間上下限差值計算標準誤[31]，公式如下：

(95%upper limit95%lower limit)/3.92公式（1）

編碼由本團隊兩名具有教育技術專業背景的研究者完成，一致性系數（Cohen’s kappa）為0.86，說明編碼一致性程度較高。對于異議項，經多次討論后達成一致。編碼結果如表1所示。

表1 編碼結果

4 調節變量設置

完成特征值編碼后，本研究結合Hew等[32]的研究設置調節變量，包含情境性因素和方法論因素：①情境性因素即學科和出版年份。大量研究者通過一階元分析檢驗教育游戲應用學科對效應量的影響，但得到的研究結論并不相同，這意味著學科作為調節變量的影響有待進一步探究。另外，有二階元分析研究提出一階元分析研究的出版時間可能會對合并效應量產生影響[33]，因此本研究將檢驗學科和出版時間對合并效應量的影響。②方法論因素即效應量獨立性和研究質量。其中，效應量獨立性是指一階元分析研究樣本中的效應量獨立，其對應的實證研究樣本只能使用一次。Borenstein等[34]提出，使用非獨立效應量可能會導致研究結果出現偏差。考慮到特征值編碼過程中發現的使用非獨立效應量現象，本研究將檢驗效應量獨立性作為調節變量的影響。而研究質量是指一階元分析研究的規范性。本研究使用Kung等[35]提出的一階元分析研究質量評價工具R-AMSTAR評價研究質量，并將評價結果劃分為優、良、中、差四個等級。由于各一階元分析研究的得分相近，故將劃分標準設置為：得分在百分位數75以上為優，得分在百分位數50～75之間為良，得分在百分位數25～50之間為中，得分在百分位數25以下為差。研究質量評價同樣由團隊的兩名研究者共同完成。

5 數據分析

本研究的數據分析過程如下：①計算合并效應量。參考Steenbergen-Hu等[36]提出的二階元分析效應量計算方法，從每項一階元分析研究中提取樣本量、效應量和標準誤，并按照原始數據錄入。考慮到納入研究的樣本相對較少，因此將這些效應量統一轉化為Hedges’s g值。在此基礎上，結合樣本量加權處理得到合并效應量。合并效應量的計算方式根據異質性檢驗結果決定，即若存在較高異質性，則使用隨機效應模型；反之使用固定效應模型。②判斷是否存在發表偏倚。發表偏倚（Publication Bias）是指與無統計學上顯著性意義的研究結果相比，有統計學上顯著性意義的研究結果更可能被發表，它直接影響元分析研究結果的可信度和說服力。發表偏倚情況一般通過漏斗圖、Egger’s回歸和Begg’s檢驗等方式判斷，上述檢驗方式均將在本研究中使用。③檢驗調節效應。即通過亞組分析檢驗調節變量的影響，其判斷依據在于觀察組間效應的計算結果是否顯著。合并效應量計算、發表偏倚檢驗和調節效應分析均采用CMA 2.0軟件。

三 研究結果

1 合并效應量分析

本研究首先進行異質性檢驗，結果如表2所示，I2=82.123%、Q=72.719（＜0.001），說明研究樣本存在較高異質性，因此選擇隨機效應模型計算合并效應量。從計算結果來看，合并效應量（Hedges’s g）為0.513，95%置信區間為0.393～0.632（＜0.001）。

表2 異質性檢驗結果

效應模型效應量標準誤95%置信區間異質性檢驗結果 下限上限QdfpI2 固定效應模型0.40.0230.3550.44672.719130.00082.123 隨機效應模型0.5130.0610.3930.632

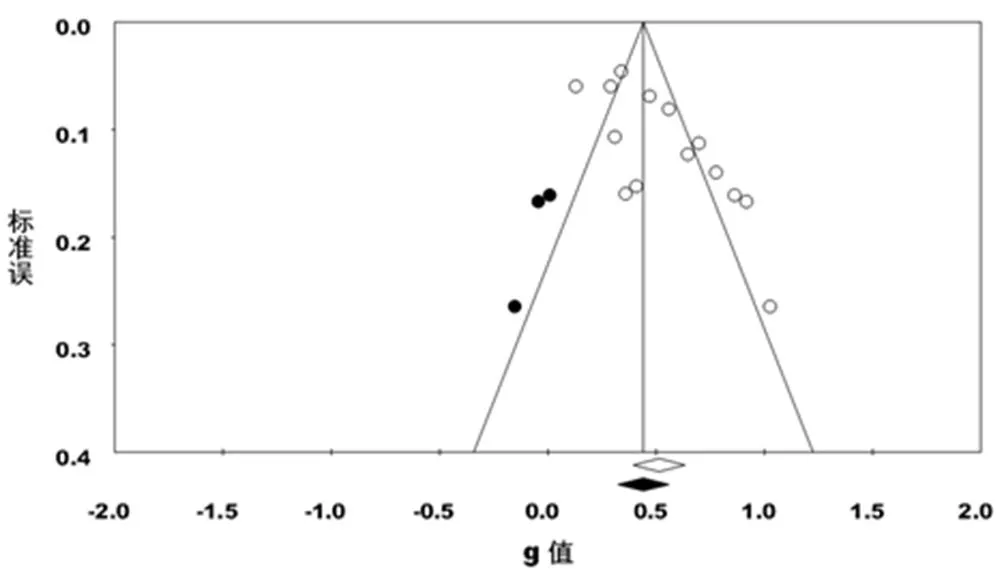
圖1 漏斗圖

2 發表偏倚檢驗

本研究得到的漏斗圖如圖1所示，可以發現修正前研究樣本并未均勻分布在左右兩側，且不具有對稱關系。Egger’s回歸結果為=3.465（＜0.05），Begg’s檢驗結果為Z=2.628（＜0.05），說明可能存在一定發表偏倚。因此，為了保障研究的準確性和可信度，采用剪補法修正合并效應量。估算和填充缺失值后，合并效應量由0.513調整為0.441，95%置信區間為0.323～0.558。

3 調節效應分析

本研究得到的調節效應分析結果如表3所示，可以看出學科、效應量獨立性和研究質量的組間效應顯著（＜0.05），出版時間的組間效應不顯著（＞0.05）。在學科方面，語言類學科（=0.759）具有較高的效應量，科學（=0.403）和數學（=0.13）的效應量相對較低。在效應量獨立性方面，效應量獨立的一階元分析研究效應量（=0.592）高于效應量非獨立的一階元分析研究（=0.294），且標準誤更小。在研究質量方面，研究質量為差的一階元分析研究具有最高效應量（=0.831），其次是研究質量為良（=0.547）和研究質量為優（=0.515）的一階元分析研究，研究質量為中的一階元分析研究效應量最低（=0.403）。

表3 調節效應分析結果

調節變量類型效應量數效應量（g）標準誤95%置信區間組間效應Qb(p) 下限上限 學科科學40.4030.0690.2680.53841.38*** 數學10.130.060.0120.248 語言類30.7590.0830.5950.922 綜合類60.5440.0880.370.717 出版時間2013～201740.4850.1090.2720.6992.49（0.288） 2018～201960.4410.10.2460.637 2020～202140.6350.0850.4690.802 效應量獨立性是110.5920.0710.4540.7316.283* 否30.2940.0960.1070.482 研究質量優50.5150.0960.3260.7039.677* 良30.5470.2490.061.035 中40.4030.0620.2810.524 差20.8310.1240.5891.074

注：*＜0.05，***＜0.001。

四 結果討論

1 教育游戲對學生學習效果的整體影響

研究結果表明，教育游戲對學生學習效果具有正向影響（=0.441），說明與不使用教育游戲相比，使用教育游戲后學生的學習效果更好，這可能與教育游戲的情境性、交互性、趣味性和高參與度有關。通過游戲場景搭建和挑戰性任務設置，教育游戲能夠為學生創設虛擬學習情境，提供及時、有效的干預與反饋，有助于激發學生參與興趣，提高學生的內在學習動機，降低無關認知負荷，進而提升學生的學習效果[37]。根據Cohen[38]提出的效應量統計標準，0.441可被看作具有中等程度的正向影響效應，與早期的元分析研究結果相比有所提升[39][40]，但提升的效應量不大（約0.1）。對此，教育工作者可能會對使用教育游戲抱持觀望態度，原因在于此前很多教師持有游戲與學習對立的觀念。根據趙永樂等[41]提出的教師對教育游戲的接受模型，中等程度的正向影響效應雖然在一定程度上有助于轉變教師對教育游戲的使用傾向和主觀態度，增加教師對教育游戲積極作用的認同，但由于教師長期以來形成的對游戲的懷疑與抵觸以及部分學校缺少必要的軟硬件資源支持和教學實踐機會，故實現教師完全采納并合理使用教育游戲仍有一定距離。從長遠來看，教育游戲有效性的持續提升是轉變教師觀念的重要推動力。

2 教育游戲對學生學習效果影響的調節因素

在情境性因素上，學科的調節作用顯著，并且教育游戲在語言類學科的應用效果較好，在數學學科的應用效果相對較差。已有的一階元分析研究也發現了類似現象[42]，究其原因，可能與學科屬性及游戲機制有關。語言感知和語言應用是語言學習的重要環節，根據雙重編碼理論[43]，教育游戲中包含的視覺和聽覺元素能夠更好地解釋單詞或短語含義。同時，一些角色扮演類游戲還能提供特定場景下使用語言交流的機會，有助于學生語言理解能力和應用能力的提升。而在數學學科，當前教育游戲對學生學習提供的幫助多集中在數字計算、圖形識別等基礎能力的培養上，難以支持邏輯推理、數學抽象等高階思維能力的培養[44]。因此，相對有限的游戲類型可能制約了教育游戲在數學學科中的應用效果。此外，數學教育游戲在開發過程中缺少充分理論支持也可能是造成上述現象的原因。具體來說，數學認知是研究個體在完成數學任務時大腦內在工作機制的學科，然而當前尚未形成數學認知與數學教育之間的有效轉化途徑[45]，這導致教育游戲開發者對學生數學學習的內在規律認識不足，所設計游戲的科學性難以得到保障，進而影響了應用效果。對于出版時間的調節作用不顯著這一結果，可能的解釋是受到一階元分析研究的樣本分布情況影響。具體來說，一項近年發表的一階元分析研究很可能包含十幾年前或更早出現的實證研究，而這些實證研究很可能已被納入早期發表的其他一階元分析研究樣本。從數據分析的角度來說，上述做法導致二階元分析研究很難準確判斷時間對合并效應量的影響，以及不同時期教育游戲對學生學習效果影響的差異。因此，建議后續一階元分析研究調整文獻檢索方式，將檢索年限縮小，以近五年或近十年開展的實證研究或以在具有特殊研究意義時間段出現的實證研究為研究對象，通過整合這些研究獲得更具代表性的研究結論。

在方法論因素上，效應量獨立性和研究質量均能夠調節教育游戲對學生學習效果的影響。效應量獨立性方面，本研究發現相較于包含非獨立效應量的一階元分析研究，只包含獨立效應量的一階元分析研究能獲得更高的效應量，且標準誤更小，這一結果印證了已有研究的推斷，即將非獨立效應量納入數據分析，可能會導致分析結果出現偏差[46]。對此，研究者可通過計算非獨立效應量均值、選擇最重要的效應量或使用多層元分析模型分析數據等方式，降低非獨立效應量的不利影響。研究質量方面，本研究結果與教育領域其他二階元分析研究相比[47]，既有相同點，也有不同點——相同點是研究質量為差的一階元分析研究效應量相對較高，不同點是研究質量為優的一階元分析研究效應量并非最低。對于相同點，可能的解釋是研究質量較差的一階元分析研究在研究方法嚴謹程度上不足，會導致合并效應量計算出現偏差，出現效應量過高、標準誤過大等不可靠的結論。對于不同點，可能的解釋是研究質量較好的一階元分析研究嚴格遵循元分析研究標準，合理控制了人為因素對研究結果的干擾，能保障研究結果的穩定性并得到較高的合并效應量[48]。另外，在使用R-AMSTAR量表劃分研究質量等級的過程中，由于樣本中一階元分析研究得分相近，本研究截取百分位數25、50、75所在的分值來劃分等級區間，這是一種“相對”的等級劃分方式。而Young[49]使用固定區間來劃分等級，這是一種“絕對”的等級劃分方式。研究質量等級劃分標準的不同，很可能是導致研究結論存在差異的主要原因。

五 研究啟示與反思

根據研究結果，本研究提出有關教育游戲設計與應用的啟示。同時，結合研究過程，本研究反思了二階元分析的優勢與局限，并闡述了研究者使用二階元分析時需要注意的事項。

1 研究啟示

本研究發現，教育游戲對學生學習效果具有中等程度的正向影響效應，且在不同學科的應用效果存在差異。因此本研究認為，對教育游戲開發者來說，應與時俱進更新游戲設計理念，積極借鑒教育神經科學、學習科學研究成果，豐富游戲數量及類型，開發面向特定學科、特定主題的教育游戲，特別是與數學學科核心素養培養相關的教育游戲；應根據學生個性化需求調整教育游戲運行機制，圍繞學生在游戲過程中可能出現的認知負荷過高、注意力不集中等問題構建應對策略。此外，可以在游戲開發過程中充分融入虛擬現實、自適應學習等技術，增強游戲的沉浸感和代入感，通過搭建豐富多樣的游戲場景和設置難度適宜的游戲任務，促進學生學習效果的提升。對教師來說，應轉變對教育游戲的認識，正視教育游戲在提升學生學習成效的積極作用，積極推進教育游戲應用。同時，教師在使用教育游戲的過程中，應基于學科特征和游戲特征，合理選擇游戲類型，精心設計教學活動，在實踐中探索基于教育游戲的教學方式。

2 二階元分析的應用反思

相比于一階元分析，二階元分析能夠降低二階抽樣誤差和發表偏倚的不利影響，減少合并效應量偏差，但也存在一定局限：①研究范圍相對有限，能檢驗的調節變量較少。二階元分析以一階元分析研究為研究對象，意味著研究主題相近是樣本篩選的重要標準。為避免出現研究樣本不足的情況，二階元分析的研究主題通常需要具備良好的一階元分析研究基礎，而對文獻數量的要求無形中也縮小了可選擇的研究范圍。另外，由于相似主題的一階元分析研究往往存在一定的研究設計差異，導致很難從中提取出普遍具有的變量，因此二階元分析能夠檢驗的調節變量往往較少。②對樣本信息的要求較高，導致實際納入的研究數量較少。如果一階元分析研究無法提供必要的樣本信息，則該文獻很可能被排除在外。原因在于二階元分析需要保障統計獨立性，而統計獨立性的檢驗標準是實證研究重疊比例保持在可控范圍內。樣本信息不全的一階元分析研究很難提取出實證研究項，因此也無法與其他一階元分析研究對比，明確樣本信息重疊情況。綜上，未來開展二階元分析研究，一方面要注意所選擇的研究主題是否具備良好的研究基礎，并根據一階元分析研究信息尋找新的調節變量，探究合并效應量背后的規律；另一方面要嚴格制定研究樣本納入標準，合理控制樣本信息重疊比例，以保障研究結果準確可靠。

[1][37][40]Clark D B, Tanner-Smith E E, Killingsworth S S. Digital games, design, and learning: A systematic review and meta-analysis[J]. Review of Educational Research, 2016,(1):79-122.

[2][29]Wilson D B, Lipsey M W. The role of method in treatment effectiveness research: Evidence from meta-analysis[J]. Psychological Methods, 2001,(4):413-429.

[3]Dekkers J, Donatti S. The integration of research studies on the use of simulation as an instructional strategy[J]. The Journal of Educational Research, 1981,(6):424-427.

[4][5][15][16][28][30]Schmidt F L, Oh I S. Methods for second-order meta-analysis and illustrative applications[J]. Organizational Behavior and Human Decision Processes, 2013,(2):204-218.

[6][19][32]Hew K F, Bai S, Huang W, et al. On the use of flipped classroom across various disciplines: Insights from a second-order meta-analysis[J]. Australasian Journal of Educational Technology, 2021,(2):132-151.

[7][25]Martin F, Sun T, Westine C, et al. Examining research on the impact of distance and online learning: A second-order meta-analysis study[J]. Educational Research Review, 2022,36:100438.

[8][39]Wouters P, Van Nimwegen C, Van Oostendorp H, et al. A meta-analysis of the cognitive and motivational effects of serious games[J]. Journal of Educational Psychology, 2013,(2):249-265.

[9]和文斌,董永權.教育游戲對學生學習效果的影響研究——基于41項實驗和準實驗的元分析[J].現代教育技術, 2021,(4):44-50.

[10]Chen M H, Tseng W T, Hsiao T Y. The effectiveness of digital game‐based vocabulary learning: A framework‐based view of meta‐analysis[J]. British Journal of Educational Technology, 2018,(1):69-77.

[11]Tokac U, Novak E, Thompson C G. Effects of game‐based learning on students’ mathematics achievement: A meta‐analysis[J]. Journal of Computer Assisted Learning, 2019,(3):407-420.

[12]Riopel M, Nenciovici L, Potvin P, et al. Impact of serious games on science learning achievement compared with more conventional instruction: An overview and a meta-analysis[J]. Studies in Science Education, 2019,(2):169-214.

[13][42]段春雨.教育游戲對學生學業成就影響研究——基于48項實驗與準實驗研究的元分析[J].開放教育研究,2017,(4):65-75.

[14]李玉斌,宋金玉,姚巧紅.游戲化學習方式對學生學習效果的影響研究——基于35項實驗和準實驗研究的元分析[J].電化教育研究,2019,(11):56-62.

[17][22][36]Steenbergen-Hu S, Makel M C, Olszewski-Kubilius P. What one hundred years of research says about the effects of ability grouping and acceleration on K-12 students’ academic achievement: Findings of two second-order meta-analyses[J]. Review of Educational Research, 2016,(4):849-899.

[18][33]Causadias J M, Korous K M, Cahill K M. Are Whites and minorities more similar than different? Testing the cultural similarities hypothesis on psychopathology with a second-order meta-analysis[J]. Development and Psychopathology, 2018,(5):2009-2027.

[20]Tamim R M, Bernard R M, Borokhovski E, et al. What forty years of research says about the impact of technology on learning: A second-order meta-analysis and validation study[J]. Review of Educational Research, 2011,(1):4-28.

[21]鄭昊敏,溫忠麟,吳艷.心理學常用效應量的選用與分析[J].心理科學進展,2011,(12):1868-1878.

[23][26][27]Cooper H, Koenka A C. The overview of reviews: Unique challenges and opportunities when research syntheses are the principal elements of new integrative scholarship[J]. American Psychologist, 2012,(6):446-462.

[24][47][49]Young J. Technology-enhanced mathematics instruction: A second-order meta-analysis of 30 years of research[J]. Educational Research Review, 2017,22:19-33.

[31]Higgins J, Thomas J, Chandler J, et al. Cochrane handbook for systematic reviews of interventions[M]. Hoboken: John Wiley & Sons, 2019:143-176.

[34]Borenstein M, Hedges L V, Higgins J P T, et al. Introduction to meta-analysis[M]. Hoboken: John Wiley & Sons, 2009:215-216.

[35]Kung J, Chiappelli F, Cajulis O O, et al. From systematic reviews to clinical recommendations for evidence-based health care: Validation of revised assessment of multiple systematic reviews (R-AMSTAR) for grading of clinical relevance[J]. The Open Dentistry Journal, 2010,4:84-91.

[38]Cohen J. A power primer[J]. Psychological Bulletin, 1992,(1):155-159.

[41]趙永樂,蔣宇,何瑩.我國教師對教育游戲的接受與使用狀況調查[J].開放教育研究,2022,(1):51-61.

[43]Clark J M, Paivio A. Dual coding theory and education[J]. Educational Psychology Review, 1991,(3):149-210.

[44]Byun J, Joung E. Digital game-based learning for K-12 mathematics education: A meta-analysis[J]. School Science and Mathematics, 2018,(3-4):113-126.

[45]裴蕾絲,尚俊杰.學習科學視野下的數學教育游戲設計、開發與應用研究——以小學一年級數學“20以內數的認識和加減法”為例[J].中國電化教育,2019,(1):94-105.

[46]Nakagawa S, Santos E S A. Methodological issues and advances in biological meta-analysis[J]. Evolutionary Ecology, 2012,(5):1253-1274.

[48]Ioannidis J P A. How to make more published research true[J]. Revista Cubana de Información en Ciencias de la Salud (ACIMED), 2015,(2):187-200.

Research on the Impact of Educational Games on Students’ Learning Effects Based on the Second-order Meta-analysis

ZHAO Du-qing SHEN Chao YU Liang[Corresponding Author]

As an important way to support students’ learning and improve their learning performance, educational games have been widely concerned by researchers and teachers for a long time. Previous meta-analysis studies on the impact of educational games on students’ learning effects are usually based on first-order meta-analysis,but have some sampling errors and are easily affected by publication bias, and the credibility of their findings is often questioned. Compared with the first-order meta-analysis, the second-order meta-analysis can improve the accuracy of research results by integrating empirical research on a large scale. Based on this, this paper reviewed the first-order meta-analysis of the impact of educational games on students’ learning effects, and explained the basic principles of second-order meta-analysis. Subsequently, this paper used second-order meta-analysis to analyze 11 first-order meta-analysis papers to explore the overall effect of educational games on students’ learning effects and its moderators. Finally, based on research results, this paper put forward suggestions on the design and application of educational games, and summarized the advantages and limitations of second-order meta-analysis, expecting to provide a reference for the development of educational games and meta-analysis research.

second-order meta-analysis; educational game; learning effect; second-order sampling error

G40-057

A

1009—8097（2022）10—0043—10

10.3969/j.issn.1009-8097.2022.10.005

本文受2019年度教育部人文社會科學研究規劃基金項目“基于情境融合的泛在學習資源個性化推薦方法研究”（項目編號：19XJA880011）、2020年度重慶市高等教育教學改革研究重點項目“構建‘互聯網+’條件下的新型課堂教學模式研究”（項目編號：202051）資助。

趙篤慶，在讀碩士，研究方向為學習科學與技術，郵箱為zhaoduqing@email.swu.edu.cn。

2022年3月25日

編輯：小時