斷控層析速度建模方法研究與應用

鄧勇， 李芳， 彭海龍， 任婷， 劉國昌

1 中國石油大學(北京)油氣資源與探測國家重點實驗室， 北京 102249 2 中海石油(中國)有限公司湛江分公司， 湛江 524057 3 中海石油(中國)有限公司海南分公司，海口 570000

0 引言

隨著勘探開發力度的逐步加大，準確獲取地下地質構造形態及展布特征是當前油氣藏開采工作的重要基礎.尤其在復雜斷塊區域，真實的地震成像是推動區域油氣藏勘探開發的重要保障(張昌榕等，2018).然而，常規的成像方法難以獲取該區域準確的成像，使復雜斷塊區域的勘探開發陷入瓶頸.為更好的應對上述挑戰，目前采用疊前深度偏移(Prestack Depth Migration，PSDM)方法解決上述問題(秦寧，2020).

在疊前深度偏移方法中，速度模型的精度制約著偏移成像的準確度，常用的速度建模方法包括速度分析法、層析反演方法、波動方程類方法等(王艷香等，2021).分析類方法存在條件假設，速度分析結果精度低，一般只用于初始速度建模(劉定進等，2019).波動方程方法的反演結果依賴于初始速度模型的精度，且需要多次迭代才能完成速度反演，效率較低(曹呈浩等，2020).而層析反演方法應用過程簡單方便，具有較好的反演精度和反演效率，是當前應用最為廣泛的速度建模方法(徐嘉亮等，2021).

傳統的射線類走時層析反演方法一般采用規則網格單元的模型參數化方式表征空間坐標問題，在復雜地質構造速度場反演過程中，需要對網格進行精細剖分(郭振波等，2019)，但是在不規則阻抗界面區域中，該方法容易出現誤差，給反演結果帶來假象(徐嘉亮等，2020).目前常規解決策略是采用不規則網格單元進行模型參數化，可以較好地表征不規則異常體的波阻抗界面(何雷宇等，2017).但上述方案并沒有完全解決斷層引起的速度差異性問題，限制了斷層區域速度建模精度的提升.除此之外，應用模型正則化方法，將地質構造特征引入層析進行約束，能夠提升層析質量，但是在復雜斷塊區域中，該方法由于缺少斷層的約束控制，反演結果中缺少高波數的速度成分，因此該方法有待進一步提升速度反演精度(李輝等，2015).

為解決斷層區域的速度精度問題，Birdus(2007)以斷層作為條件，在密集的疊前深度偏移道集網格上進行非雙曲剩余曲率分析，然后約束速度更新過程.該方法需要高密度道集，且只能在與斷層對應的有限區域內進行約束控制.Rodriguez等(2011)將斷層上下盤分為兩個區域分別進行速度反演，但該方法僅更新斷層附近的速度，且在更新過程中難以實現有效迭代.Guo等(2015)提出用斷層附近道集的剩余曲率來約束層析正則化過程，能夠更新整個模型.但是準確拾取斷層附近反射信息的剩余曲率較為困難，因此，該方法在應用中存在一定的挑戰.

為更好地改進層析成像在復雜斷塊區域速度建模的精度問題，本文在模型正則化層析的基礎上，提出一種基于斷層控制的層析方法，該方法對成像過程中的斷層進行識別判斷，利用斷層數據構建預條件矩陣，然后采用TV正則化方法改進目標泛函，從而避免層析過程中斷層兩側速度的平滑過渡，提升斷層兩側的速度場精度，得到分辨率較高的斷塊區域速度.經實際鉆井數據驗證，該方法得到的速度場和實際速度場匹配度高，具有較好的應用效果.

1 方法理論

在地震反演過程中，多個不同的解都適合作為同一個地球物理問題的解，使得反演問題具有不確定性.為解決上述問題，層析反演一般采用先驗約束降低多解性，常用的方法是正則化(張力起等，2019).正則化是將逆問題的先驗信息和逆解估計的期望加入到反演過程中，從而消除反演過程的病態問題，提高反問題求解的魯棒性和適定性(代榮獲等，2019).地球物理反問題中，通過增加正則約束來解決病態反演問題取得了很好的效果.盡管無法獲得描述真實地下介質的完全精確解，但可以得到滿足應用需求的近似最大似然解(蘇揚等，2021).

正則化技術是獲得有地質意義解的有效方法，按照應用條件一般可分為模型正則化和數據正則化.模型正則化利用地下構造信息約束模型參數，實現改善估計模型參數的目的(張兵和王華忠，2019)；數據正則化是在層析中加入空間介質參數的數據關聯性(李輝等，2015)，但是收斂效率較低，收斂效果較差，目前應用較少.按照正則化函數的不同，正則化技術可以分為Tikhonov正則化和總變差(TV，Total Variation)正則化.相比較而言，Tikhonov正則化計算過程穩定，但是難以保持層析過程中的速度邊界，TV正則化能夠較好的保持速度的邊緣信息，但是穩定性較差(王永奎等，2022).

在反演過程中引入模型的相關認識，即構成模型正則化.模型正則化的實現策略主要包括Tikhonov模型正則化和預條件模型正則化，預條件模型正則化方式收斂性又優于模型約束的Tikhonov模型正則化，且計算效率較高，因此本文采用預條件正則化進行層析矩陣構建，得到精度相對較高的初始速度.然后以此為基礎，對成像數據中的斷層進行識別判斷，通過識別的斷層數據建立預條件矩陣并采用TV正則方法改進目標泛函，實現速度場的更新，得到復雜斷塊區域的高精度速度場.

(1)預條件模型正則化

層析反演采用匹配射線走時的方法來得到速度值，應用射線追蹤方法擬合地震數據中的反射信息走時，并通過走時差的反投影得到速度的更新量(范白濤等，2022).對于實際地震數據而言，拾取的地震走時可以表示為：

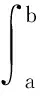
(1)

式中，τobs表示拾取的走時，s表示觀測數據慢度，dl表示沿著射線路徑ab的射線長度.如果已知背景慢度，則計算的走時可以表示為：

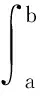
(2)

式中，τcal表示計算的走時，s0表示背景慢度，則走時擾動和慢度擾動具有如下關系：

(3)

將式(3)轉為矩陣，則基于射線的線性走時層析反演表達式為：

Lδs=δτ，

(4)

式中，L表示線性化算子.由(4)式可知，每一條射線都存在一個對應的公式，所有射線所代表的公式則構成一個射線層析方程組，因此基于貝葉斯反演理論的最大后驗概率密度思想，層析反演的目標泛函為：

(5)

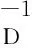
層析反演在迭代過程中，采用線性化方式對目標函數進行優化，則線性迭代方程為：

(6)

式中，矩陣A表示A(m)的線性化算子，Δm表示當前迭代次數下的模型更新量，Δd表示當前迭代中的數據殘差.

通過公式(5)和公式(6)中的數據協方差矩陣和正則化參數，能夠對層析反演過程實現正則化.在不考慮正則化的情況下，即協方差矩陣為單位矩陣且阻尼因子為0，意味著僅用數據殘差進行層析反演，則公式(6)退化為一般的層析方程：

Δd=AΔm.

(7)

ASu=Δd，

(8)

Δm=Su，

(9)

式中：S表示預條件算子，u為預條件的解.考慮阻尼因子ε，則層析方程的阻尼最小二乘方程可以表示為：

STATASu+εu=STATΔd.

(10)

將預條件下的解u=S-1A-1Δd代入方程(10)并適當變換得到：

SSTATAΔm+εΔm=SSTATΔd，

(11)

對于公式(11)而言，如果將地質構造信息引入預條件算子S，則公式(11)就是構造約束正則化的層析方程.所以，提取地質構造信息，并將其引入預條件算子所表示的光滑矩陣是上述步驟的關鍵點.

在同一個空間坐標系下，不同的散射點的位置和傾角信息具有較大的差異性，為構建一個空間上的光滑矩陣，可以通過坐標變換的方式將上述地質信息融入到變換后的光滑矩陣中(萬弘等，2017)，空間坐標的轉換示意圖如圖1所示.

圖1 坐標變換示意圖Fig.1 Schematic diagram of coordinate transformation

圖1中，逆時針方向表示旋轉的正方向，局部地質坐標系原點為散射點中心，記為T(u,v,w)，u軸的方向就是反射界面的走向，w軸方向是反射界面垂直方向；空間坐標系記為T′(x,y,z).然后參照李輝等人提出的坐標轉換方法，空間坐標經過一系列的旋轉、平移后變換為局部地質坐標系(李輝等，2015).記散射點的原始空間坐標為T′(x0,y0,z0)，則旋轉后的局部地質坐標可以表示T(u0,v0,w0)，兩個坐標系存在以下關系：

采訪正值“第十九屆國產高濃度磷復肥產銷會”期間，楊三可來到甕福集團展臺，向國內外客商推介甕福集團“DAP+”、磷酸二氫鉀、聚磷酸銨等新型增效肥料。

(u0,v0,w0)=T(x-x0,y-y0,z-z0)，

(12)

式中，T為旋轉矩陣，滿足條件：

(13)

式中：φ和θ分別表示坐標變換中x和z坐標軸的旋轉角度.兩參數在地質意義中分別表示地層方位角和傾角.

光滑矩陣的某一行元素就是一個光滑函數，用于描述不同介質點之間的聯系，令此光滑函數為高斯光滑函數，則光滑矩陣中第i行第j列的元素為：

(14)

式中，σui,σvi,σwi分別是高斯函數在局部地質坐標系中不同方向上的標準差.實際應用過程中，通常默認地下介質為均勻層狀結構，認為反射界面方向模型參數基本一致，垂直于反射界面方向的模型參數變化劇烈，因此水平方向對應的光滑范圍相對較大，即σui、σvi要大于σwi，則相應的標準差可以通過式(15)、(16)計算：

σui=σvi=abs(sin(φ))，

(15)

σwi=ξσui，

(16)

式中，ξ表示參數因子，通常取0.2～0.5的一個常數，至此將地質構造信息引入光滑矩陣.由于高斯函數的方差求取簡單快速，可以作為一個已知量，所以構建光滑矩陣的關鍵點就是求取地質構造的傾角和方位角信息.

(2)地層傾角方位角計算

在成像剖面中，可以拾取主要反射同相軸作為某一套地層的頂底界面，以此為基線進行界面之間層位的插值，通過計算頂底界面的相關地層信息，然后結合地層接觸關系則可以依次得到整套地層的傾角和方位角信息.開展上述工作時，首先要判斷頂底界面之間地層的接觸關系，通過地層關系實現整套地層信息的計算.根據地層沉積規律，頂底界面之間的地層應當存在連續沉積、侵入式沉積、剝蝕沉積等地層關系，具體如圖2所示.

確定好頂底地層接觸關系后，頂底地層之間的其他地層可以通過插值進行恢復，從而建立整個工區的地層架構.地層架構一旦確立，可以根據幾何定理得到人工解釋層位數據的傾角方位角，地層傾角方位角的幾何關系如圖3所示.圖3中，θx表示x方向的視傾角，θy表示y方向的視傾角，θ表示地層的真傾角，ω表示地層的方位角.利用人工解釋地層數據信息，分別在x方向和y方向建立網格，目標點位于中心，解釋數據位于網格交點上，則數據位置分布如圖4所示.

通過圖3和圖4，則目標點的視傾角、真傾角和方位角的公式為：

tanθx=Δx/Δz，

(17)

tanθy=Δy/Δz，

(18)

(19)

(20)

式中，Δx、Δy和Δz分別表示目標點和四周8個點不同方向上坐標的差值加權結果.完成頂底解釋地層的方位角傾角計算后，則解釋地層之間的地層傾角方位角可以采用圖5的原理進行計算.

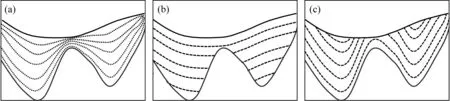
圖2 不同沉積模式示意圖(a) 等比例連續沉積； (b) 等厚底面侵入沉積； (c) 等厚頂面剝蝕沉積.Fig.2 Schematic diagram of different sedimentary modes(a) Equal proportion continuous deposition； (b) Equal thickness bottom intrusive sedimentation； (c)Equal thickness top denudation deposition.

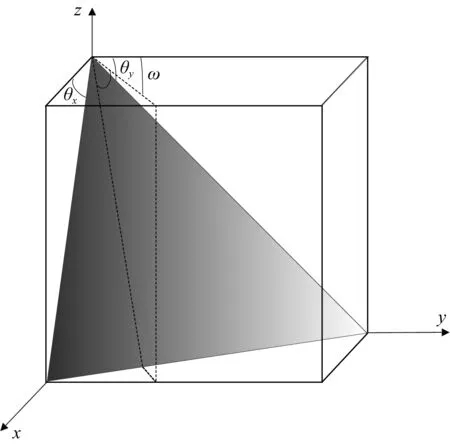
圖3 地層傾角方位角幾何信息示意圖Fig.3 Schematic diagram of geometric information of formation dip angle and azimuth angle

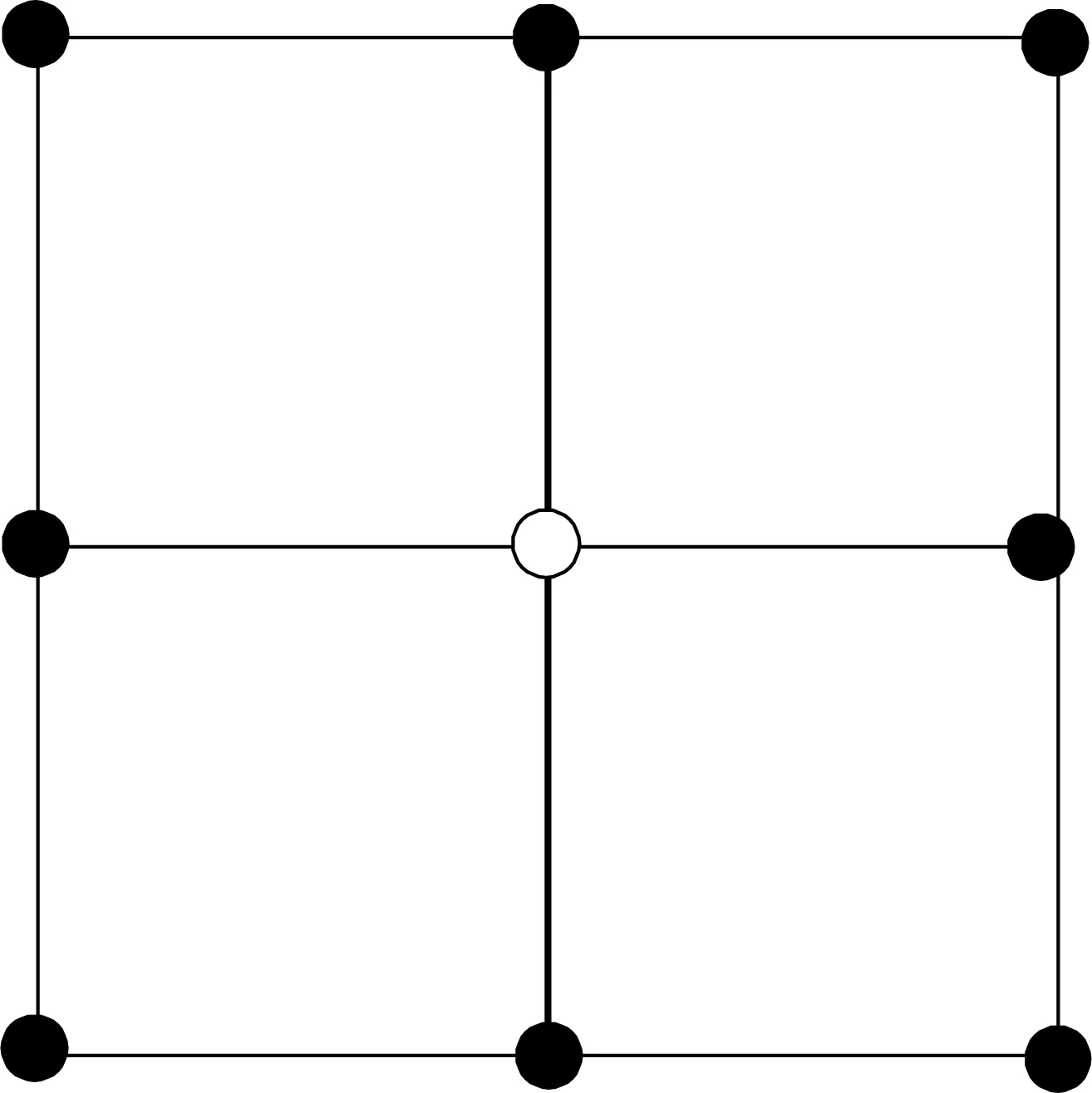
圖4 層位網格示意圖Fig.4 Schematic diagram of horizon grid

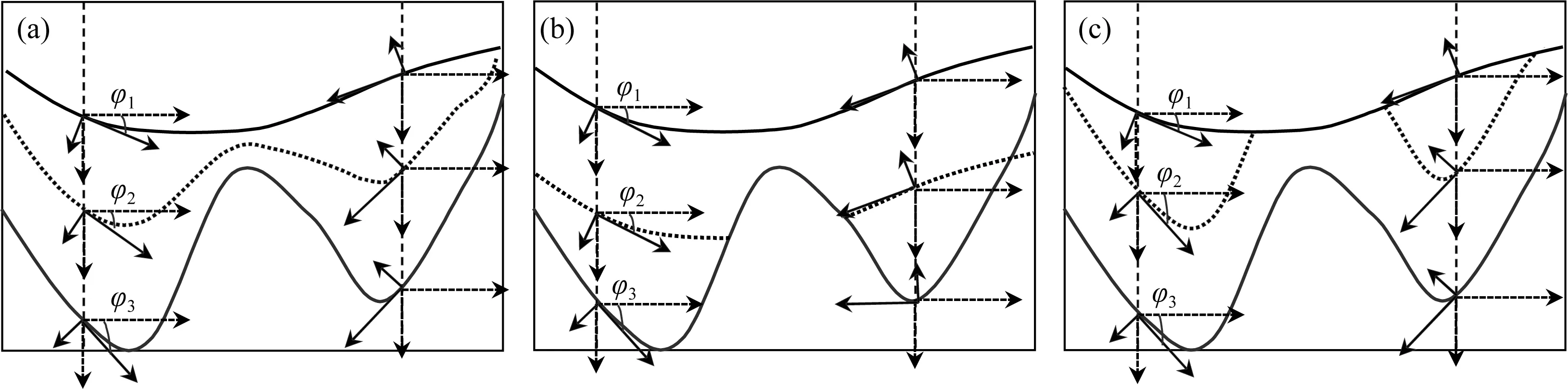
圖5 不同沉積模式下地層傾角計算示意圖(a) 等比例連續沉積地層信息關系； (b) 等厚底面侵入沉積地層信息關系； (c) 等厚頂面剝蝕沉積地層信息關系.Fig.5 Calculation diagram of formation dip angle under different sedimentary modes(a) Information relationship of equal proportion continuous sedimentary strata； (b) Information relationship of sedimentary strata invaded by equal thickness bottom； (c) Information relation between denudation sedimentary strata of equal thickness top surface.

在圖5a表示等比例連續沉積，設定頂界面在平面坐標某位置處的角度為φ1，同一平面坐標位置處，底界面角度為φ3，則同一平面坐標位置處的中間某一深度的地層角度φ2為：

(21)

式中，H1表示頂界面的深度值，H3表示底界面的深度值，H2表示目標位置處的深度值，在圖5b中，地層接觸關系為等厚底面侵入關系，則中間地層的地質信息和頂界面地層一致.在圖5c中，展示的是等厚頂面剝蝕地層的接觸關系，中間地層的地質信息和底界面地層一致.結合圖5所示的不同地層接觸關系，運用公式(21)可以計算整個工區的構造信息.

(3)斷層控制正則化

公式(11)引入構造信息后，可以得到較為準確的速度反演結果，但斷層區域速度精度依舊有待提升，因此如何構建一個斷層控制的目標泛函是關鍵.

預條件模型正則化方法會使得斷層區域的速度邊界模糊，難以保持斷層兩側的速度差異性，因此有必要采用新方法提高斷層兩側速度的精度.考慮TV正則化具有保持邊緣信息的特征，可以在預條件模型正則化的基礎上引入TV正則化.TV正則化在重構模型參數過程中，能夠得到更為準確和豐富的參數信息，但是需要異常邊界信息的支持，從而加快收斂速度，提高收斂精度，因此可以在重構算法中引入斷層邊界約束控制方法.根據當前迭代成像結果中斷層邊界位置信息，構建權重矩陣并將其用于下一次迭代，從而形成邊界約束的TV正則化方法，則改進后正則化的目標泛函可以表示為：

(22)

式中，‖‖1表示L1范數，D表示三維梯度算子稀疏矩陣，其主要作用是對速度模型中的每一個速度值做梯度運算，在每次迭代過程中，使探測得到的參數邊界避免正則化，從而保持該位置附近的參數邊界；S表示預條件光滑矩陣.然而，在實際計算過程中，TV正則化存在著不穩定性，因此需要將公式(22)轉為線性化方式進行求解，然后通過多次迭代并不斷修正模型參數，使最終的反演結果不斷逼近真實值.

對于模型參數的修正，需要采用迭代加權方式求解，通過對一系列權系數不斷更新的加權最小二乘問題進行計算，得到目標函數的最優解.采用加權方式將L1范數松弛轉為L2范數，則公式(22)轉變為：

(23)

式中，ε和β表示正則化參數，取值為[0,1]，用于調節不同約束項的權重，w表示對角矩陣，其公式可以表示為：

(24)

對于一個Nx×Ny×Nz的層析網格，當i=1,2,…,Nx，j=1,2,…,Ny，k=1,2,…,Nz時，則梯度算子矩陣可以表示為：

(25)

由實際地質特征可知，斷面左右的速度具有一定的差異性，要想保持斷層兩側速度突變的真實性，就需要公式(23)在計算速度值梯度算子時不能跨越斷層兩側，也就是位于斷面網格位置處的速度值不能和斷面兩側的速度值同時參與梯度計算，因此可以將上述斷層代表的邊界信息以權重矩陣的形式參與下一次迭代.即將此邊界與公式(23)正則化過程結合，基于上述思想，則構建的對角權重數組表達式為：

(26)

式中P(xi,yj,zk)表示xi,yj,zk位置處網格坐標，F(Φ)表示解釋的斷層數據坐標集，W表示三維矩陣.

由公式(26)可知，矩陣的建立不受斷層類型的影響，一旦獲取到斷層的位置坐標，就可以建立對角權重矩陣.定義斷層控制的三維誘導矩陣Γ為：

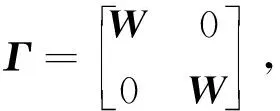
(27)

將上述權重矩陣公式代入公式(23)，則公式變為：

(28)

隨著速度場更新，斷層在空間上會發生飄移，斷層更新后的實際位置已經偏離最初解釋的斷層位置，因此需要對斷層位置進行推測識別，采用新的斷層信息對層析過程進行約束控制.

為提升斷層的識別精度和提取效率，本文采用各向異性擴散方程中的梯度結構張量來提取地質構造特征，通過特征向量的情況來識別斷層，則三維網格中梯度結構張量的計算公式為：

(29)

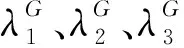
(30)

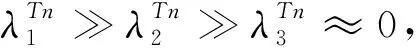
圖6 特征值和空間地質結構關系圖Fig.6 Relationship between eigenvalues and spatial geological structure

為提升流程效率，只需對目標區域的主斷層區域進行斷層控制模型更新，因此需要應用人工解釋的斷層數據F(Φ)對計算得到的斷層位置集合Fn進行預估，其中F表示斷層數據(三維)集合，Φ表示人工解釋斷層，n表示第n次迭代.速度模型的更新對于斷層位置偏移量影響相對較小，因此可以定義偏移量來時預估新的斷層位置集，如果推測出的斷層位置集合Fn∈F(Φ+Δf)，則認為是目標斷層區域.根據該處定義可知，即使人工解釋斷層刻畫位置存在誤差，只要在一定范圍內，可以通過后續更新后的斷層來約束斷層位置.其中Δf表示定義的空間位置誤差項，然后將計算得到的斷層數據引入公式(24)和公式(27)，并結合公式(23)，則建立的斷層控制矩陣的目標泛函可以表示為：

(31)

LW(mn)=(TΓn)Tdiag[max(ΓnTmn,γ)p-2]ΓnT，

(32)

+βLW(mn)mn，

(33)

(35)

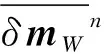
(36)

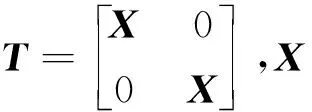
通過上述方法，速度更新過程可以很好的保護斷層區域速度的差異性，可以解決常規層析反演方法在該區域中遇到的難題，得到斷層區域較為準確的速度值.

2 理論模型

為驗證本文方法，建立一個含有復雜斷層構造的地質模型，該模型含有多個斷層，然后在此基礎上開展正演，進行速度分析后執行疊前深度偏移.其中，真實速度模型剖面以及采用常規速度層析方法得到的偏移結果剖面如圖8所示.

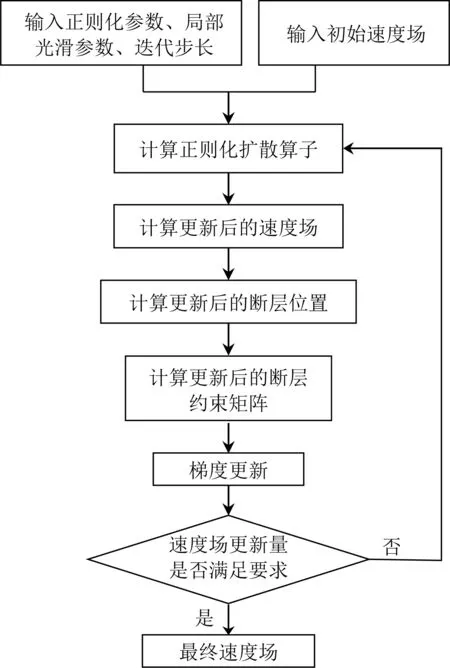
圖7 斷控層析速度建模流程算法示意圖Fig.7 Schematic diagram of fault constrained tomography flow algorithm

對比圖8可知，常規層析速度建模方法得到的成像剖面，其構造形態和原始速度模型大體一致，但是斷層下方區域成像質量較差.因此該區域的成像質量有待進一步改善.在圖8成像剖面的基礎上，解釋層位和斷層數據，然后計算地層的傾角(所有地層方位角為同一數值)，則計算的地層傾角數據剖面如圖9所示.在上述解釋數據、傾角和方位角數據的基礎上，建立斷層約束算子，則速度更新前后的剖面對比如圖10所示.最后將基于斷控層析速度建模方法得到的速度應用于PSDM，則兩種不同速度反演方法得到偏移成像結果如圖11所示.

對比圖10和11可知，采用斷控層析反演方法得到速度，能夠更好的描述斷層區域的速度分布情況，斷層兩邊的速度截斷和實際情況也較為匹配.采用斷控層析速度進行PSDM，斷面成像更清晰，斷層下部的地層成像更為連續，成像質量更好.

3 實際數據應用

選取南海某工區的實際地震數據進行測試，該區域斷裂系統發育，斷裂結構復雜，導致很難獲取該工區準確的速度場，從而使得偏移成像結果不可靠，嚴重影響該區域的勘探開發進程.為解決上述問題，本文采用斷控層析速度建模方法獲取準確的速度場，從而有效提高PSDM成像準確度.

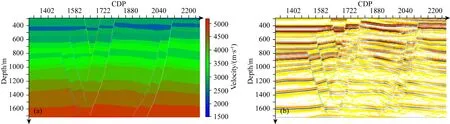
圖8 速度模型及PSDM成像剖面Fig.8 Velocity model and PSDM imaging profile

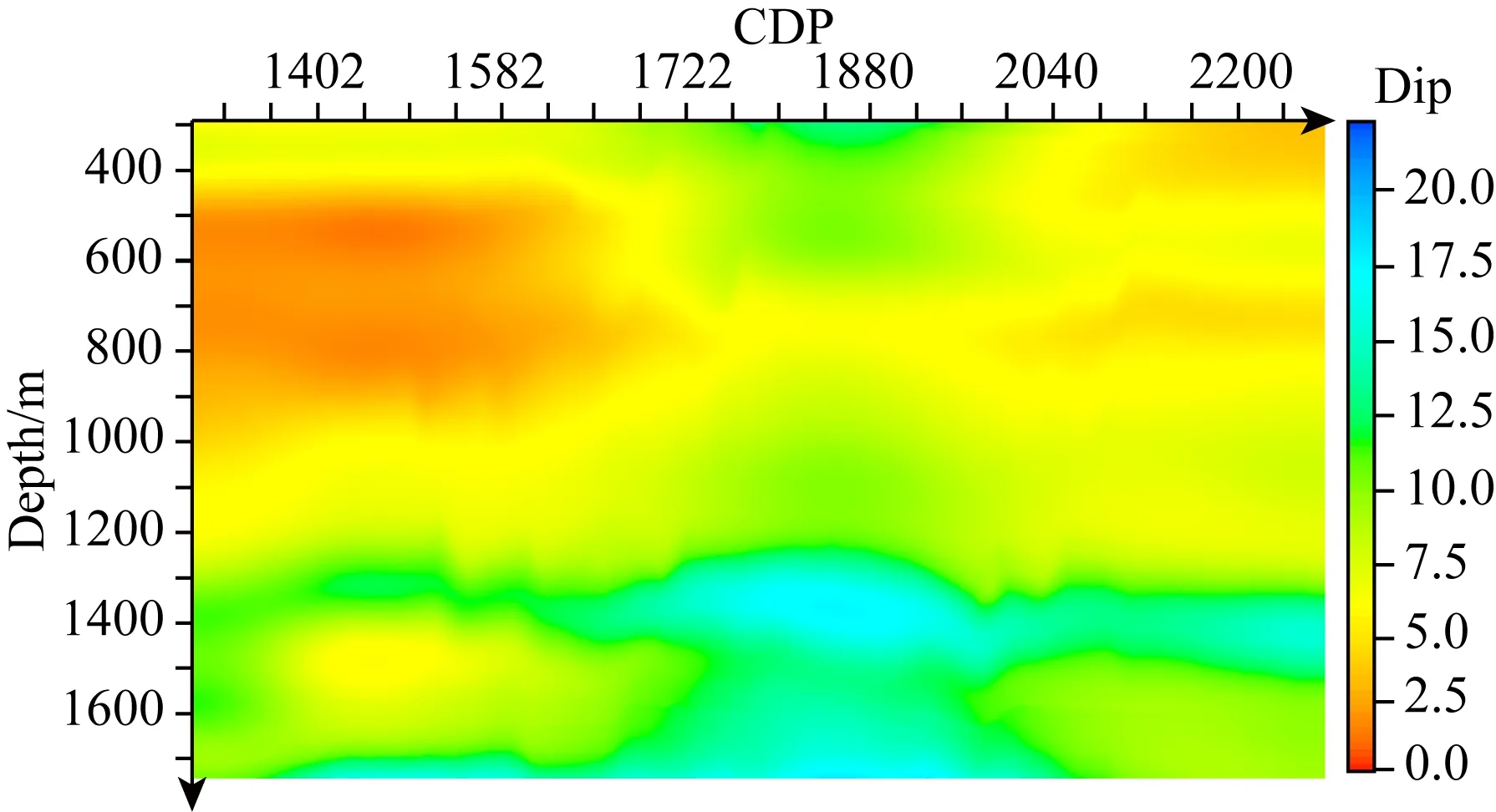
圖9 計算的地層傾角數據剖面Fig.9 Calculated dip data profile

(1)地層傾角方位角數據的計算

為準確計算地層的傾角和方位角，首先需要根據地質沉積規律來準確判斷地層之間的接觸關系，其次分析區域的實際地質情況，考慮地層和斷層、地層與地層、斷層與斷層之間的接觸關系，圖12展示一條二維線上主要斷層解釋數據分布情況.

由圖12可知，該區域地層和地層之間都是等比例沉積，所以只需要計算出區域主地層的傾角和方位角即可，然后利用公式(17)計算該區域所有地層傾角和方位角，計算的地層傾角和方位角如圖13和圖14所示.

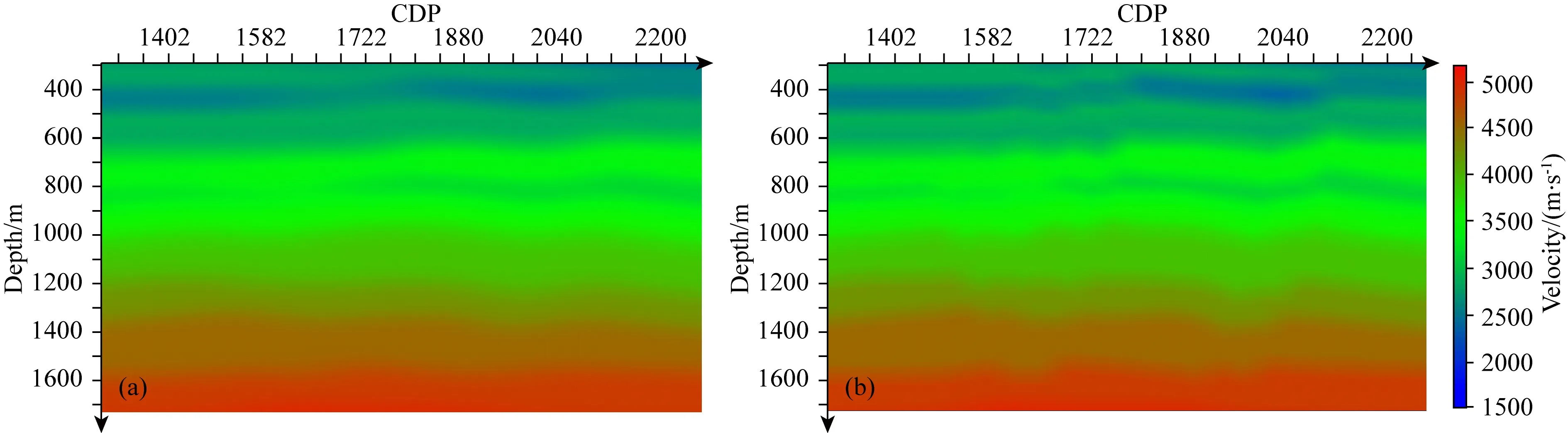
圖10 不同速度反演方法結果對比(a) 常規層析方法反演結果； (b) 斷控層析反演結果.Fig.10 Comparison of results of different velocity inversion methods(a) Inversion results of conventional tomography； (b) Fault controlled tomography inversion results.

圖11 不同速度建模方法的到的PSDM剖面(a) 常規層析反演方法得到PSDM剖面； (b) 斷控層析反演方法得到PSDM剖面.Fig.11 PSDM profiles with different velocity modeling methods(a) PSDM profile obtained by conventional tomography inversion method； (b) PSDM profile obtained by fault controlled tomography inversion method.

圖12 解釋數據剖面Fig.12 Interpretation data profile

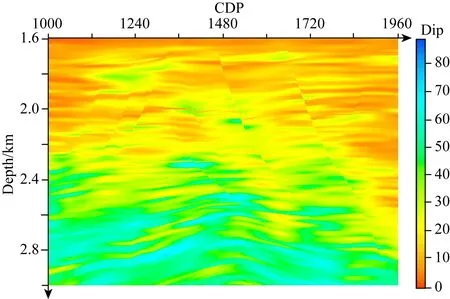
圖13 計算的地層傾角剖面示意圖Fig.13 Calculated dip profile

在速度更新過程中，需要采用梯度結構張量對斷層的位置進行重新識別.隨著速度的變化，部分斷層的位置發生飄移，但是整體偏移位置不大.經過速度更新后，采用梯度結構張量來識別工區內的斷層，則本研究工區中識別的斷層位置和原始人工解釋斷層的疊合情況如圖15所示.

由圖15可知，速度更新后，梯度結構張量自動識別的斷層位置和原始人工解釋斷層位置存在一些差異，但是位置的差異量不大.且根據識別結果可知，在部分區域，即使沒有人工解釋斷層，很多小斷層也被識別出來.為了盡可能提升計算效率，目前只需將解釋斷層附近被識別出斷層數據引入層析過程.根據解釋斷層的位置，選取附近更新后并被識別出的斷層數據，將其用于斷控層析速度建模，從而實現速度的更新.對于識別出來其他非目標區域的斷層，其斷層數據則不用建立斷層約束算子.根據上述方式，可以利用初始解釋斷層數據匹配自動識別的斷層，采用新的斷層數據建立斷層約束算子，將其引入改進的目標函數用于速度場的迭代更新.

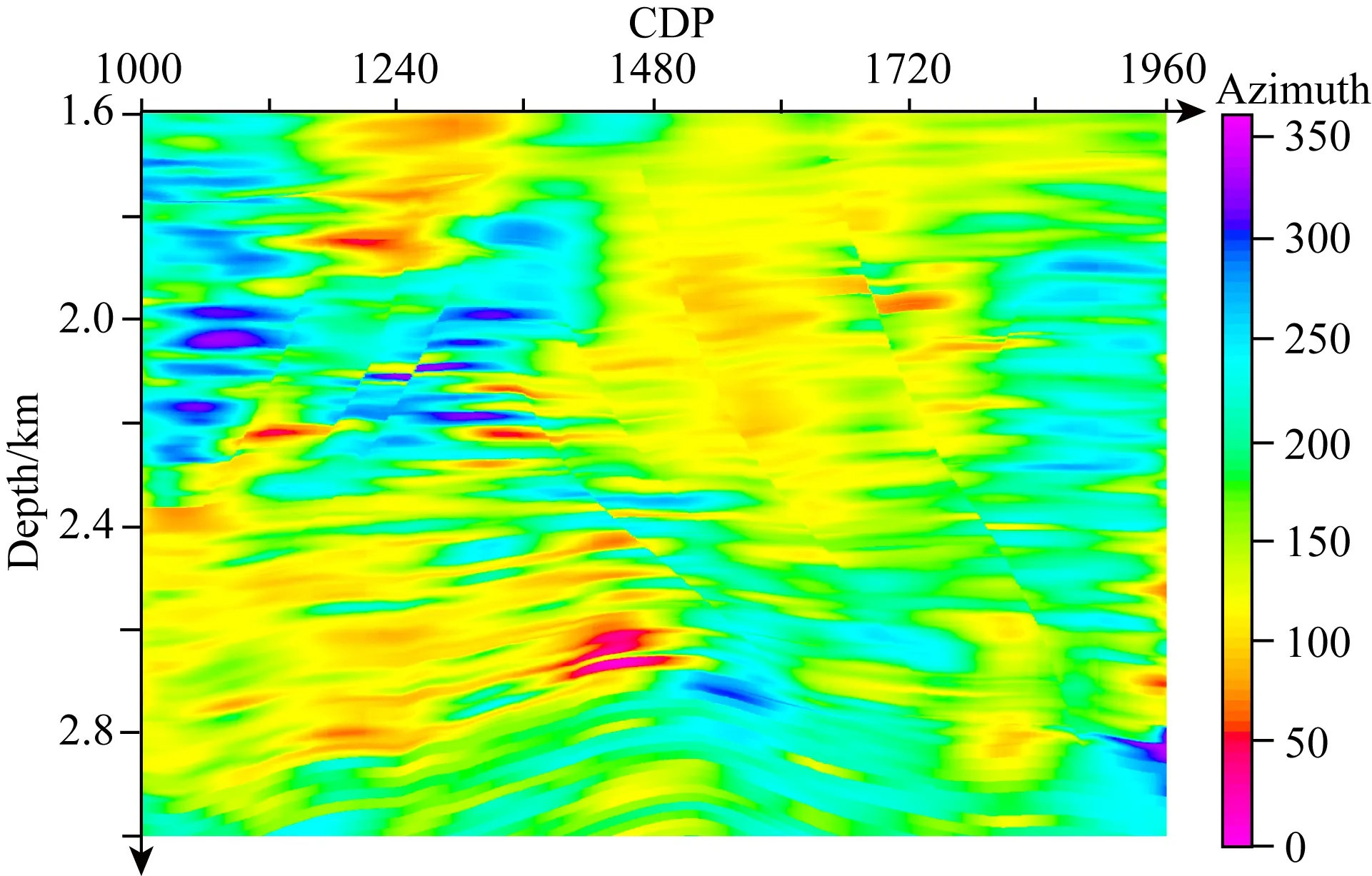
圖14 計算的地層方位角剖面示意圖Fig.14 Calculated stratigraphic azimuth profile

圖15 層析反演前后的斷層邊界示意圖Fig.15 Fault boundary before and after tomographic inversion profile

(2)斷控層析速度建模以及偏移成像

利用提出的斷層控制正則化層析速度反演方法對南海復雜斷塊區進行速度建模，在此基礎上進行疊前深度偏移.圖16和圖17分別展示了常規層析速度、斷控層析速度的剖面對比和水平切片.

斷層區域由于斷層兩側對接巖性的年代差異，會表現出速度突變現象.然而，在圖16a和圖17a中，斷層兩側速度是平滑漸變，斷層兩側速度差異不明顯.斷層約束層析反演速度建模結果中，斷層兩側速度突變明顯，斷面等其他物理性質影響體現的更為準確.為進一步分析兩種層析結果，對其成像結果再次對比，結果如圖18所示.

對比圖18可以發現，在常規方法的成像剖面中，斷層區域(藍色線框和黑色線框區域)的反射同相軸出現扭曲錯段的現象，甚至出現一條垂直的虛假斷層，上述現象的存在，嚴重干擾對斷層區域地質狀況的認識.經過分析可知，常規速度建模方法導致斷層附近的速度不準確，使得成像剖面出現虛假的垂直斷層和地層扭曲錯斷的現象.而在斷控層析反演成像結果中，虛假的垂直斷層消失，反射同相軸更加清楚和平整，表明斷層附近的速度更為準確，剖面成像質量提升明顯.

圖16 不同速度建模方法的地震-速度疊合剖面(a) 常規層析速度； (b) 斷控層析速度.Fig.16 Profile of different velocity inversion methods(a) Conventional chromatographic velocity；(b) Fault constrained tomography velocity.

圖17 不同速度建模方法的地震-速度疊合水平切片(a) 常規層析速度； (b) 斷控層析速度.Fig.17 Time slices of different velocity inversion methods(a) Conventional chromatographic velocity； (b) Fault constrained tomography velocity.

圖18 不同速度建模方法的成像剖面對比示意圖(a) 常規層析PSDM剖面； (b) 斷控層析的PSDM剖面.Fig.18 Comparison diagram of imaging sections with different inversion velocities(a) Conventional tomographic PSDM profile；(b) PSDM profile of fault controlled tomography.

為進一步分析本文方法對于成像的影響，提取兩種方法偏移成像結果的相干體屬性進行對比，結果如圖19所示.

從相干體切片中，斷控層析反演速度建模方法的成像結果優勢更加明顯.在圖19a的常規層析速度成像結果中，圓圈中斷層的識別較為模糊，地層的反射也較為紊亂，難以識別斷層的組合.然而，在圖19b結果中，地層反射規律性強，斷層位置識別清晰.

為檢查速度反演質量，進一步量化反演速度結果，利用穿過斷層的某實際鉆井數據進行驗證，井軌跡位置如圖20所示.然后采用相同的地震子波和不同的地震速度模擬地震記錄，將模擬結果和測井速度的合成地震記錄進行相關，通過相關性來判斷當前速度的精確度.圖21展示的是測井數據合成記錄同兩種速度的正演結果對比，結果表明，斷控層析速度的合成地震記錄和測井地震記錄的相關系數為0.75，常規層析速度的合成地震記錄和測井地震記錄的相關系數為0.58，證實斷控層析速度建模方法的速度結果和實際鉆井速度吻合度更高，最符合實際速度場分布情況.

4 結論

本文提出了一種基于斷層控制的層析反演速度建模方法，該方法通過地震解釋數據計算相關模型參數，建立斷層約束的正則化約束算子，以此為基礎建立斷層控制的層析反演目標泛函，利用斷層數據作為速度建模的先驗信息，采用迭代最小二乘優化方法逼近L1范數的目標泛函，提高速度建模的精度.應用本文方法獲取的速度模型，斷層區域的速度分布更加符合地質認識，模型與真實情況吻合度更高.將反演得到的速度場用于PSDM，提高了復雜斷塊區域的成像質量，為后續目標評價提供了可靠的地震成像數據，從而有助于提高復雜區油氣勘探成功率.由于相關研究條件限制，本方法的模型參數表征采用了矩形網格方式，因此在描述模型邊界的精度方面依舊存在提升空間，下一步研究計劃采用三角網格進行模型參數表征，開展層析反演的正則化研究工作.

圖19 不同反演速度的成像剖面相干體提取結果對比(a) 常規層析成像結果提取的相干體； (b) 斷控層析成像結果提取的相干體.Fig.19 Comparison of coherent volume extraction results of imaging profiles with different inversion velocities(a) Coherent volume extracted from conventional tomography results； (b) Coherent volume extracted from fault control tomography results.

圖20 穿越斷層的井軌跡示意圖Fig.20 Schematic diagram of well trajectory crossing fault

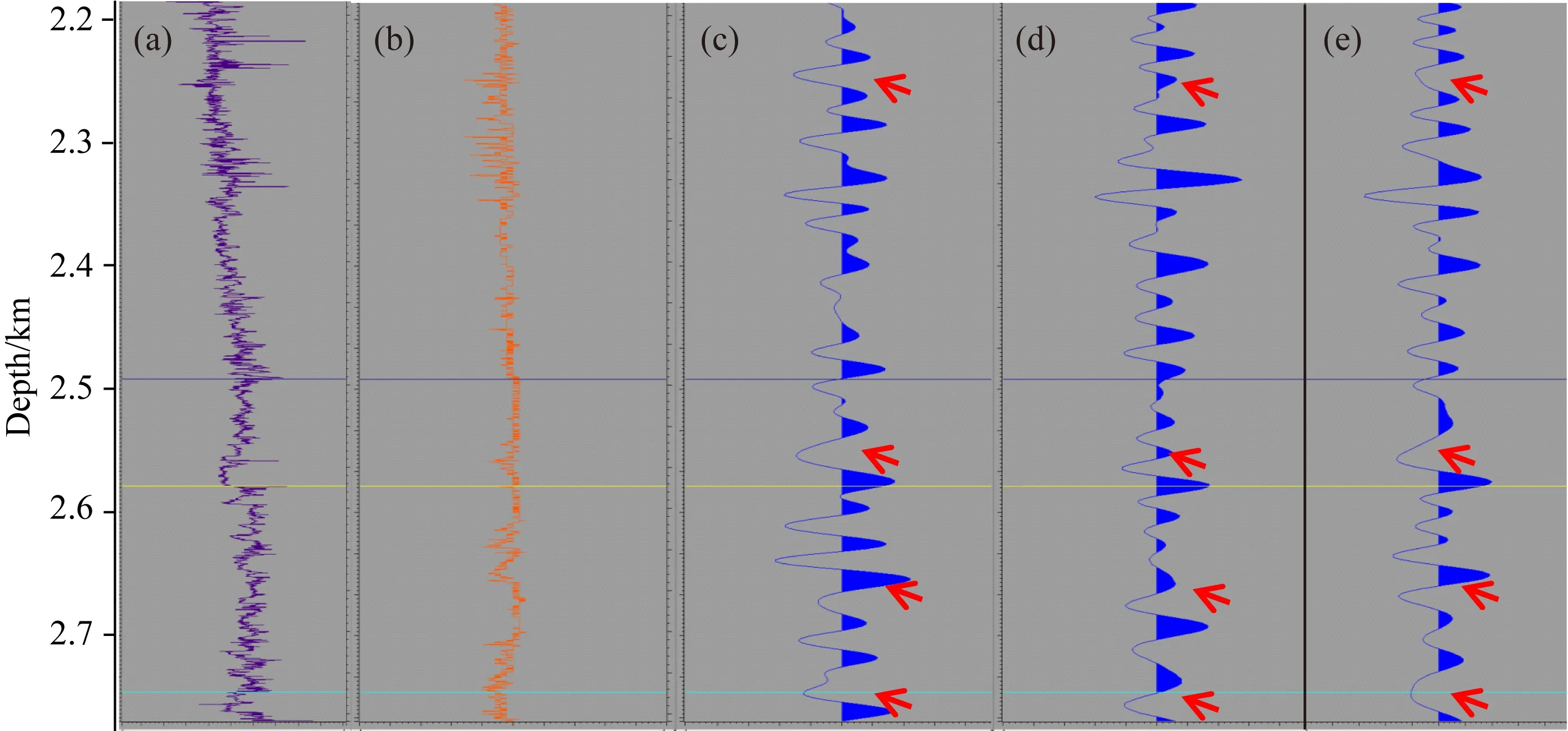
圖21 不同速度的合成記錄對比示意圖(a) 測井聲波數據； (b) 測井密度數據； (c) 測井合成記錄； (d) 常規層析反演速度合成記錄； (e) 斷控層析速度合成記錄.Fig.21 Forward comparison diagram of different velocity(a) Logging acoustic data； (b) Logging density data； (c) Logging synthetic record； (d) Conventional tomographic inversion velocity synthesis record； (e) Fault controlled tomography velocity synthesis record.