基于數字巖心孔喉特征的等效孔隙縱橫比有效性研究

譚開俊， 趙建國， 滕團余， 劉欣澤， 閆博鴻

1 中國石油勘探開發(fā)研究院西北分院， 蘭州 730020 2 中國石油大學(北京)油氣資源與探測國家重點實驗室, 北京 102249 3 中國石油天然氣股份有限公司玉門油田環(huán)慶分公司， 甘肅酒泉 735019

0 引言

巖石微觀孔隙結構形態(tài)對巖石物性具有重要的影響，以定量化儲層預測為目標，油氣勘探中對巖石微觀孔隙結構研究的要求日益提高.碳酸鹽巖儲層由于成巖后期強膠結、溶蝕、以及礦物充填等作用次生孔隙非常發(fā)育，這使其孔隙結構極其復雜(Bathurst, 1972; Lucia, 1983)，常見的有鑄模孔、粒內溶孔、粒間溶孔、晶間孔、裂縫等，Anselmetti和Eberli(1993, 1997)發(fā)現這些復雜多變的孔隙結構對彈性性質的控制作用甚至比孔隙度還大；Zhang等(2015)研究發(fā)現在中國四川碳酸鹽巖儲層中，在相同孔隙度下由于多種孔隙結構的發(fā)育其縱波速度會出現約有1000 m·s-1的速度差異；Sayers(2008)也指出具有相同飽和度、孔隙度的數據點在解釋量版上的分布并不集中.這導致我們在儲層預測時很容易將孔隙結構對速度、彈性性質造成的影響歸結在孔隙度、孔隙流體等其他因素上，使結果產生很大的偏差(李宏兵等，2019).另一方面，Anselmetti和Eberli(1999)、Eberli等(2003)還通過分析裂縫與孔洞的分布發(fā)現裂縫發(fā)育會顯著增強滲透率這一規(guī)律，并試圖用之來近似預測巖石滲透率.因此，孔隙結構特征的研究對碳酸鹽巖等巖性的儲層預測、含油性評價具有重要意義.

為了盡可能定量化地預測與表征孔隙結構，國內外許多學者從多種角度進行了大量的實驗與理論研究.從巖石物理實驗研究的角度出發(fā)，Anselmetti等(1998)通過圖像數字分析技術(Digital Image Analysis，DIA)提取了17塊白云巖鑄體薄片的孔隙尺寸分布、孔隙形狀(孔隙周長與孔隙面積的比值)等作為孔隙結構表征參數，隨后又使用Wyllie時間平均方程計算速度與實測速度的差值為標準，定義了300多塊碳酸鹽巖巖心的孔隙結構變化情況，最后將孔隙結構用于滲透率的預測(Anselmetti and Eberli，1999；Eberli et al.，2003).Verwer等(2010)分析指出具有較高孔隙比表面的碳酸鹽巖樣品剪切模量會明顯降低.目前使用高分辨率的掃描電鏡還能夠更進一步研究納米級的微小孔隙，三維全巖心CT成像技術可以更準確地獲得巖石內部骨架與孔隙的復雜幾何形狀(Coenen et al.，2004)，建立真實的巖石模型.此外隨著實驗手段的進步，Volokitin等(2001)將核磁共振技術應用于巖心的孔隙結構描述：首先通過離心過程獲取巖心處于不同飽和情況時的橫向弛豫時間T2譜，再由一定的標定方法與理論轉換得到孔喉半徑分布頻率.還可以對巖心進行恒速或高壓壓汞，通過進汞與退汞壓力變化曲線與相應理論依據能夠較準確地推算孔隙、喉道、孔喉比大小及含量分布，實現孔隙結構定量化研究(Wang et al.，2019；王永詩等，2021).

在巖石物理理論模型方面，眾多學者通常采用等效介質理論將孔隙結構與彈性性質聯系起來.經典的等效介質理論主要有K-T模型(Kuster and Toks?z，1974)、Mori-Tanaka(MT)模型(Benveniste，1987)和微分等效介質(Differential Equivalent Medium，DEM)模型(Berryman et al.，2002)等，這些模型均將孔隙理想化為縱橫比不同的橢球體，在此基礎上計算多孔巖石等效彈性模量.Xu和White(1995)考慮碎屑巖中的孔隙在砂巖組分與泥巖組分中具有不同的結構(孔隙縱橫比)，以DEM、K-T模型為基礎發(fā)展了著名的Xu-White模型，用以估算碎屑巖儲層的橫波速度.Kumar和Han(2005)引入了大、中、小三種縱橫比的孔隙，給出了聯合DEM模型與Wyllie時間平均方程估算三種孔隙的縱橫比及體積分數的實施流程.Xu和Payne(2009)應用Kumar的工作思路并加入泥巖孔隙，對碳酸鹽巖測井曲線進行了三種孔隙結構及含量的預測，其對孔隙結構的刻畫通過實測橫波速度與預測值的對比得到驗證.Zhao等(2013)將Kumar的孔隙分類及計算方法應用于地震數據，并通過電阻率成像測井對孔隙結構進行了驗證.Pan等(2015)、趙建國等(2021a，b)基于數字巖心也對地震孔隙結構預測方面進行了研究.而李宏兵等(2013)認為在研究孔隙結構對彈性性質的影響時，即使巖石中含有多種孔隙類型都可將其等效為具有單一縱橫比的孔隙來表示，并通過具有多重孔DEM模型與單一孔隙類型DEM模型之間的對比證明了這種等效的合理性.除了上述將巖石中孔隙等效為一種或有限的幾種結構外，David和Zimmerman(2012)考慮了巖石中含多種孔隙的情況，并通過變壓力超聲干燥測量速度數據與DEM理論反演得到了具有不同縱橫比孔隙的分布，結果通過飽和測量數據進行驗證.國內歐陽芳等(2021)也通過超聲實驗與多種等效介質理論對此方面進行了分析.然而這種方法很難應用于測井、地震等大尺度的情況.

總體上目前對孔隙結構的描述可以分成兩大類，一種是從實驗角度獲取，包括薄片、CT掃描數字巖心、掃描電鏡等直接成像手段，以及通過核磁共振、壓汞等物理實驗方法得到孔隙、喉道半徑等微觀幾何形狀參數；另外一種是將預先獲取的彈性模量聯合相應的等效介質理論，通過反演的思路計算等效孔隙縱橫比或類似參數，相比其他孔隙結構參數而言基于等效介質理論孔隙縱橫比更容易獲得，并且能夠應用于測井、地震等大尺度數據.然而，等效孔隙縱橫比畢竟是從彈性性質出發(fā)通過理論間接計算得到的，能否確切地表征巖石真實的復雜孔隙結構特征，在于其是否能夠與巖石中直接觀測到的孔隙幾何形狀參數之間建立起定量的關系(Baechle et al.，2008).雖然Anselmetti等(1998)、Baechle等(2008)使用DIA技術能夠提取鑄體薄片的孔隙結構參數，可以與DEM模型中的孔隙縱橫比建立一定的聯系，但是鑄體薄片畢竟屬于二維圖像，與三維巖心實際的孔隙空間相比有很大的差距，且不同位置的薄片結構變化或許很大.此外，使用薄片的孔隙結構參數提取缺乏明確的孔喉分割理論支撐，可能不夠精準.因而如果能夠定量化地建立孔隙縱橫比與實際巖石三維圖像的孔隙特征參數之間的聯系，那么在利用等效介質理論表征孔隙結構時，其合理性與準確性就具有了強有力的支撐，CT掃描技術無疑是最合適的手段.

本文以CT掃描數字巖心為基礎，從模擬的彈性性質和圖像提取的孔隙網絡幾何特征兩方面研究了孔隙結構的定量化表征方法，建立了等效孔隙縱橫比與孔喉特征參數間的定量關系：我們首先分別對基于數字巖心的彈性模擬技術與孔隙網絡提取方法進行介紹；然后，對砂巖與碳酸鹽巖兩類不同巖性巖心進行CT掃描，并對掃描圖像進行圖像處理以保證能精確重構三維數字巖心模型；接下來將數字巖心分割為子塊，應用上述兩種方法獲得每個子塊的等效彈性模量與多種孔喉幾何特征參數；最后，構建等效介質理論與模擬彈性模量之間的損失函數方程，通過優(yōu)化算法來計算等效孔隙縱橫比，再分別與各子塊的不同孔喉幾何特征參數進行了交會分析， 最終發(fā)現平均喉道長度和等效孔隙縱橫比有較為明顯的線性擬合關系，表明它們對孔隙結構的表征具有良好的一致性.

1 基于數字巖心的彈性模擬與孔隙網絡提取

對于物體彈性性質的數值模擬，我們使用的是Garboczi和Day(1995)提出的有限元模擬方法，它使用了靜態(tài)線彈性方程的變分形式.在數值計算時首先給定一初始位移場，利用共軛梯度算法對線彈性方程離散后的有限元控制方程進行迭代求解，計算三維數字巖心數據體內任意一體素的位移量，由位移得到應力應變值并平均得到宏觀量，再使用胡克定律即可計算巖石等效彈性模量.這種方法以彈性模量會影響物體中的應力應變分布為前提，根據最小位能原理，物體在受到應力產生應變后，會向著應變位能減小的趨勢變化，最終在應變位能最小時達到平衡狀態(tài)，利用此時物體的應力應變，計算得到的是物體處于小應變狀態(tài)下的等效彈性模量，因此是一種靜態(tài)的模擬.

從圖形幾何學的角度，在利用數字巖心圖像直接確定孔隙結構特征方面，我們使用了孔隙網絡法.這主要是因為在理想情況下，我們期望巖心內部的孔隙能夠通過聯通、分割算法(夏良正和李久賢，1999)將每部分連在一起的孔隙空間單獨標定出來，這樣就可以很容易確定孔徑、球度、表比面積等幾何形狀特征參數.然而大多數聯通在一起的孔隙空間都是極度不規(guī)則的，很難定量評價形狀特征，或者有些巖心中的孔隙空間是整體聯通的，無法對其進行分割與評價，因此需要采用特定的方法將較為復雜的孔隙空間轉化成一種形狀比較規(guī)則的空間來等價表示.受到滲流性質模擬領域的啟發(fā)，在研究中我們采用最大球方法提取了三維數字巖心的孔隙網絡.這種方法首先將不規(guī)則的孔隙空間轉化成了由大量內切球體充填的空間，對所有球體進行一定的劃分后將孔隙空間中較寬的區(qū)域定義為孔隙，孔隙之間的窄區(qū)域通過圓柱型的喉道相連接，兩者組合成為孔隙網絡.這種網絡能夠近似等效地表示巖心的孔隙空間，因此其幾何形狀特征參數就能夠表示孔隙結構特征(Dong and Blunt, 2009).

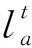
(1)

(2)

其中，ra、rb表示孔隙對應的最大球a、b的半徑，rt表示喉道最大球的半徑，k表示孔喉長度分割系數，喉道長度lt定義為喉道總長度lab減去兩個孔隙長度la、lb后的值.以上就能夠得到孔隙網絡所有的幾何特征參數. 從式(1)、(2)中可以發(fā)現，這種孔喉劃分方法是在孔、喉對應的最大球半徑與分割系數的約束下分別定義了孔隙與喉道的范圍，在喉道長度范圍內的所有最大球都歸屬于喉道，而在孔隙長度范圍內的所有最大球則歸屬于孔隙.這種方法雖然能夠簡便的獲得喉道與孔隙的長度特征，但是其中分割系數是一個人為控制的比例系數，Dong和Blunt (2009)在計算時給定為0.6，在本文中為了分析該參數對孔喉分割的影響，我們分別計算了不同系數值時的喉道長度參數并進行對比.

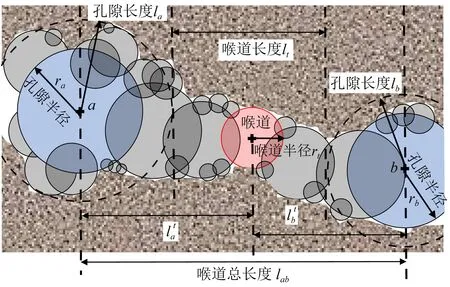
圖1 孔隙-喉道劃分示意圖Fig.1 Pore-throat segmentation

為了更好地理解孔隙空間轉換為孔隙網絡后孔、喉位置對應的孔隙空間區(qū)域，為孔隙結構的定量分析提供基礎，我們構建了由球體規(guī)則排列而成的巖石模型并提取孔隙網絡，見圖2.孔隙網絡中8個較寬的區(qū)域被定義為孔隙(紅色球體)，孔隙間的連接區(qū)域為喉道(藍色圓柱體)，這有效地實現了不同孔型孔隙空間的定量判別.為進一步分析孔隙網絡模型是否能夠對巖石宏觀整體的孔隙結構有比較定量化的表征，我們嘗試提取了有明顯孔隙結構特征巖心的孔隙網絡.圖3a中的數字巖心樣品為典型的裂縫性孔隙結構，孔隙空間成扁平狀延展，圖3c中為孔洞型的數字巖心樣品，其孔隙空間多為連續(xù)的類球狀，延展小數量多，分布較為均勻；圖3b與3d為對兩者提取的孔隙網絡模型，可以發(fā)現裂縫型樣品對應的孔隙網絡模型中，藍色圓柱狀喉道的長度大多相比孔洞型樣品的喉道要明顯更長一些，裂縫幾乎都由喉道組成.而孔洞型樣品的喉道較為短小，基本由孔隙與喉道連接而組成.統(tǒng)計喉道長度、半徑頻率分布譜，發(fā)現兩種喉道相關參數在裂縫型樣品中都要大于孔洞型樣品，分布范圍也更寬，但是其中喉道長度差別更明顯，見圖4、5，因此在下文中我們重點應用喉道長度對孔隙結構進行定量化分析.

2 數字巖心的圖像預處理

為了分析與驗證孔隙網絡模型中的孔喉參數能否定量化描述巖石的孔隙結構，我們分別選擇了孔隙結構較為復雜的碳酸鹽巖樣品和孔隙結構相對均一的砂巖樣品，共同來進行孔隙結構定量化分析與對比.所有樣品都為切割好的直徑38 mm的圓柱體，如圖6、7所示，使用本實驗室的CT設備掃描成像后得到的圖像分辨率可達每體素20.7678 μm.為了提取后續(xù)運算所需的孔隙結構信息，CT掃描原始圖像需要經過對比度增強、濾波去噪、相邊緣增強以及圖像二值化分割幾個主要的圖像處理步驟，本文以圖6中1號白云巖巖心為例來展示圖像處理的過程及效果，見圖8，處理僅對從原始圖像中心剪裁的邊長為1000體素的正方體圖像進行.

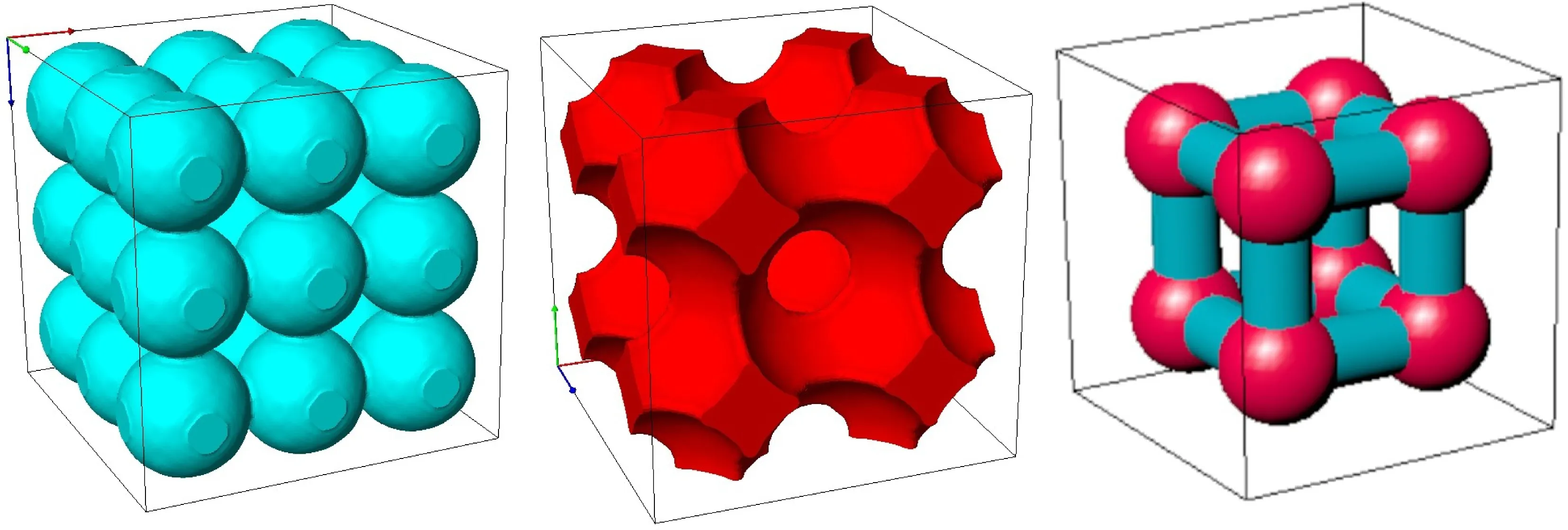
圖2 最大球法提取簡單球體堆積模型的孔隙網絡(a) 球體堆積模型骨架空間； (b) 球體堆積模型孔隙空間； (c) 球體堆積模型孔隙網絡.Fig.2 Process of pore-network extracted by maximal ball method for a simple sphere packing model(a) Skeleton of sphere packing model； (b) Pore space of sphere packing model； (c) Pore-network of sphere packing model.

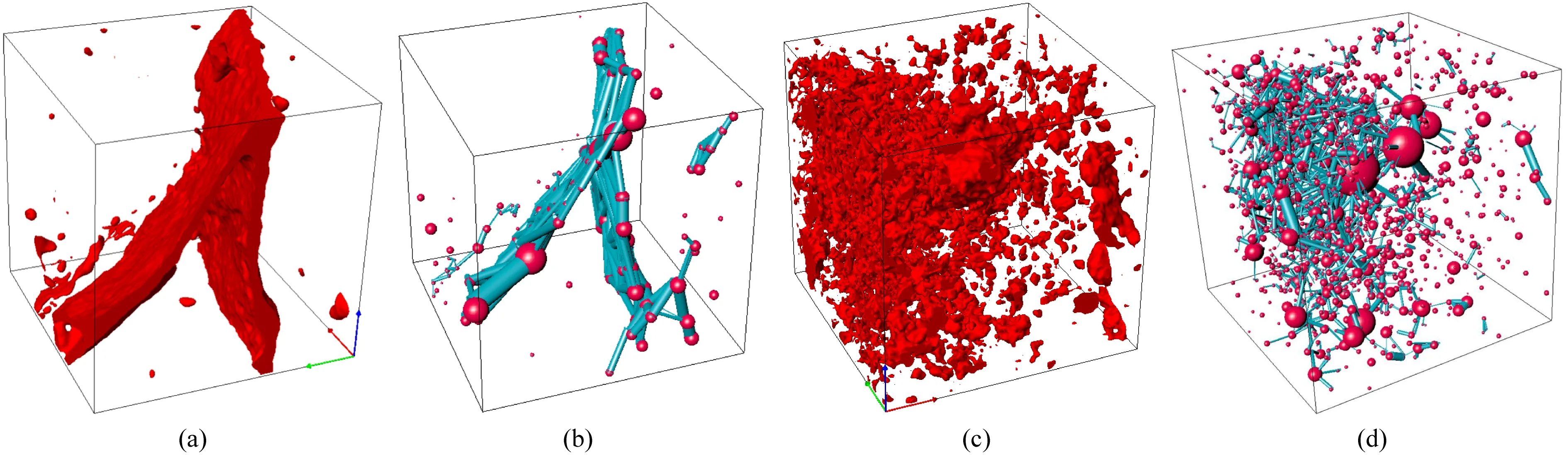
圖3 不同孔隙類型數字巖心樣品孔隙網絡提取(a) 典型裂縫型樣品數字巖心模型； (b) 裂縫型巖心孔隙網絡模型； (c) 典型孔洞型樣品數字巖心模型； (d) 孔洞型巖心孔隙網絡模型.Fig.3 Extraction of pore-network for digital core of different pore structure(a) Digital core model of typical fracture core； (b) Pore-network model of fracture core； (c) Digital core model of typical porous core； (d) Pore-network model of porous core.

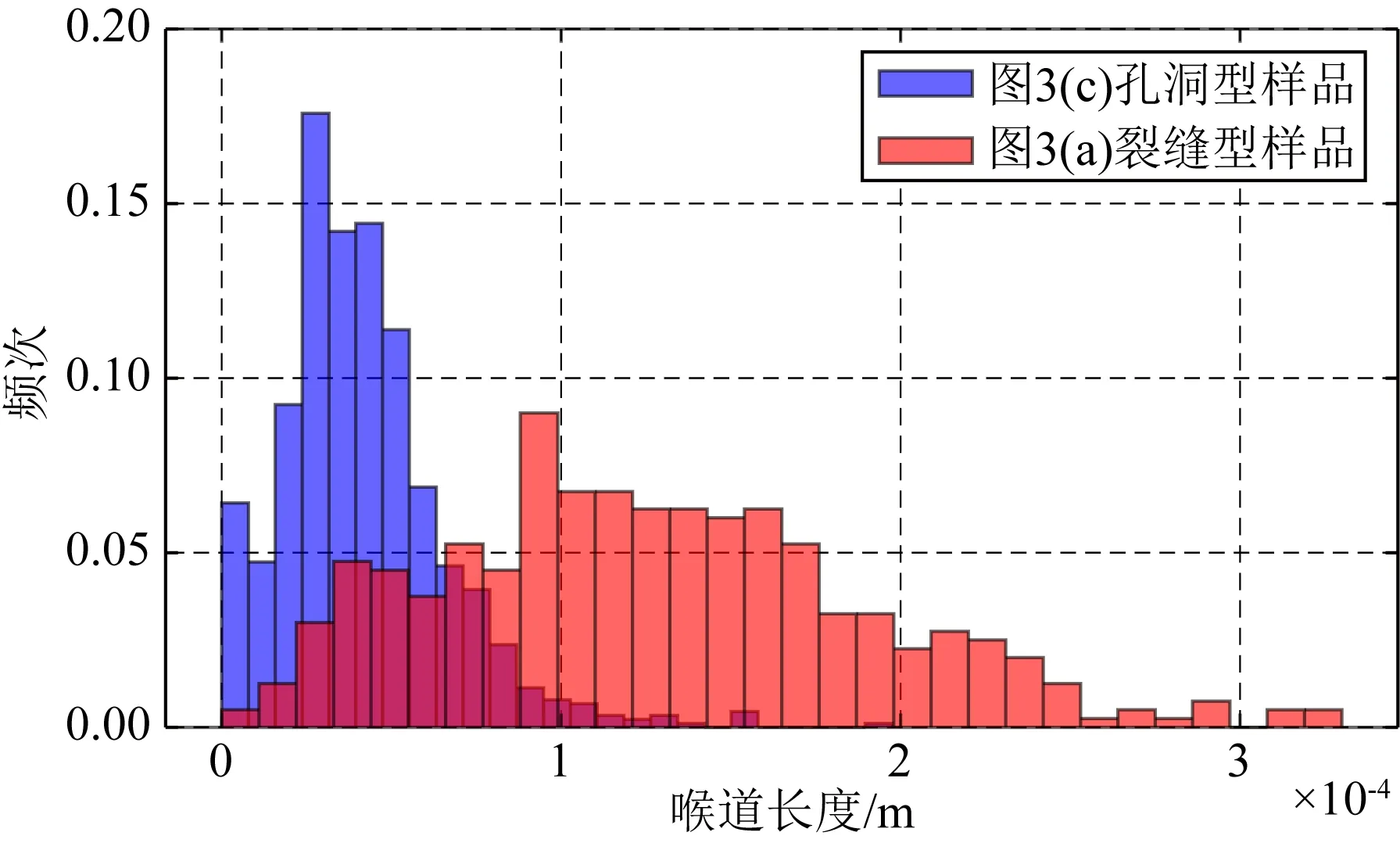
圖4 裂縫、孔洞型樣品喉道長度分布譜Fig.4 Histogram of throat length in fracture and porous cores

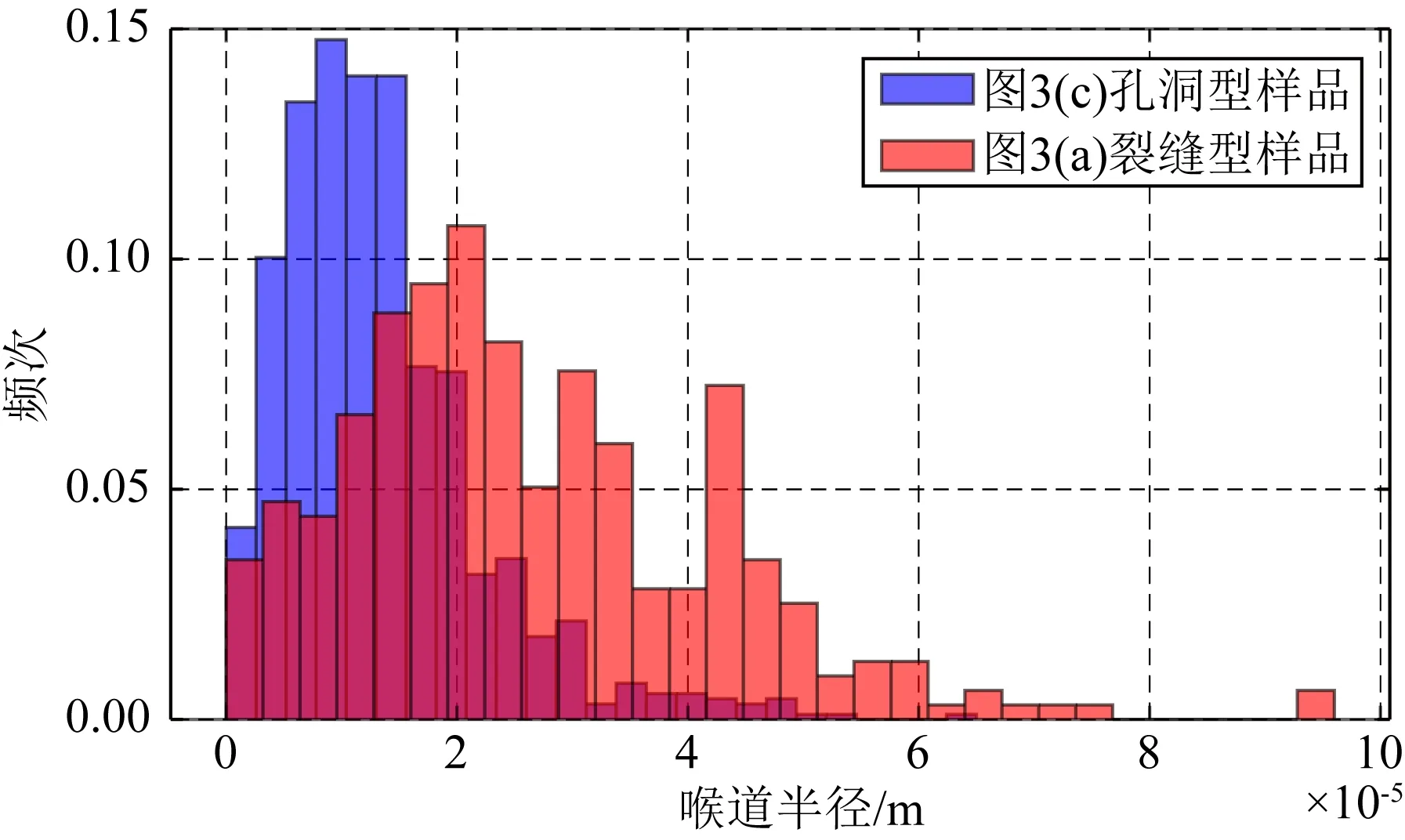
圖5 裂縫、孔洞型樣品喉道半徑分布譜Fig.5 Histogram of throat radius in fracture and porous cores

對數字巖心的圖像處理是進行彈性性質模擬及孔隙網絡模型提取的關鍵步驟，直接決定著孔隙結構定量化表征的準確性.圖6中第二排展示了7塊碳酸鹽巖樣品CT掃描成像處理后的三維孔隙空間分布情況，可以發(fā)現該類樣品具有比較復雜的孔隙結構類型、非均質性較強、孔隙度都很小，圖7中第二排展示了砂巖巖心的孔隙三維分布，直觀看來砂巖樣品的孔隙結構明顯比較單一且分布均勻，和碳酸鹽巖樣品的區(qū)別較大，孔隙度也遠大于碳酸鹽巖.

圖6 碳酸鹽巖樣品Fig.6 Carbonate sample

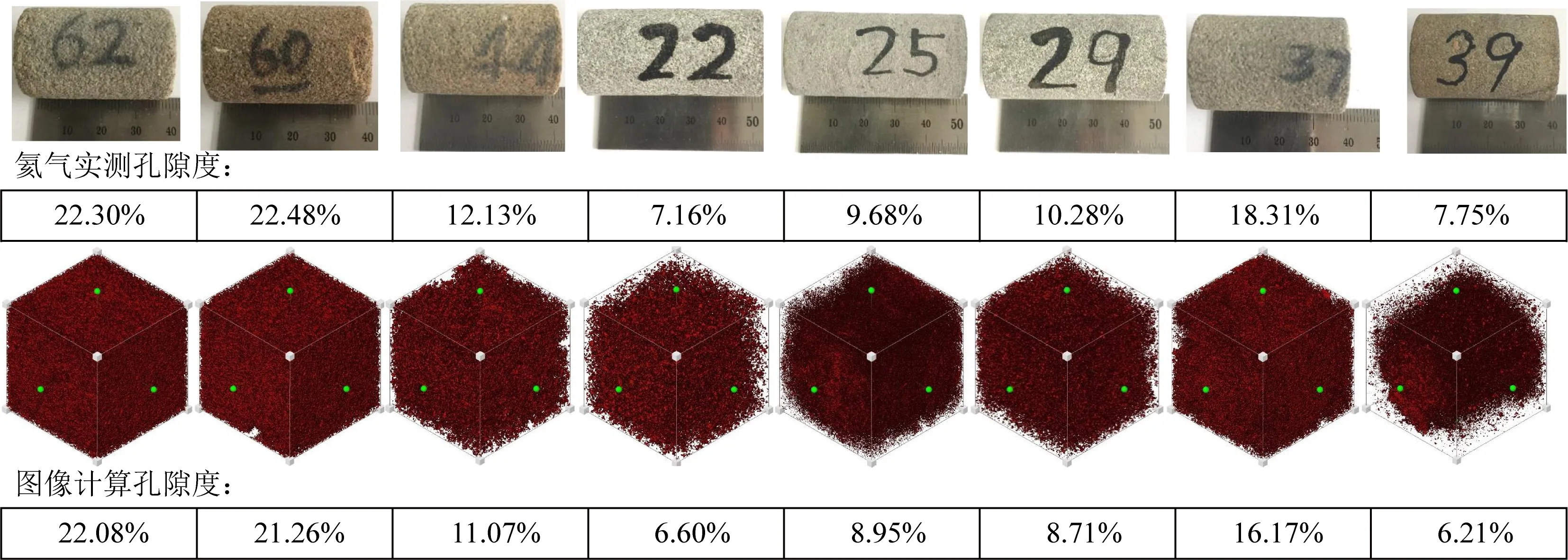
圖7 砂巖樣品Fig.7 Sandstone sample

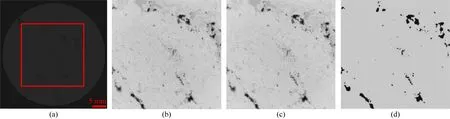
圖8 CT掃描圖像處理中間過程及結果(a) 原始掃描圖像切片； (b) 對比度增強結果； (c) 濾波； (d) 二值化分割結果.Fig.8 Result and process of CT image processing(a) Original scanned image slice； (b) Contrast enhancement result； (c) Filtering for image； (d) Binarized image segmentation result.

在后續(xù)的模擬運算前，我們還需對整個數字巖心數據進行子塊分割，這主要有兩方面的原因，首先是受限于計算機的處理能力、內存和運算所需要的時間，一般較難處理10003個體素的數據量；另外單個或少量巖心計算結果較為單一，無法分析巖心性質的統(tǒng)計性規(guī)律.對此Dvorkin等(2011)認為如果將數字巖心內部子塊數據集的模擬數據點組成趨勢線，那么這將在多個尺度上都比較穩(wěn)定，并且這樣的趨勢線不會隨巖心取樣空間位置和尺度的變化而產生劇烈波動， 因此我們需要將大正方體的巖心分割成大小合適的子塊數據.但是分割后的巖心子塊也應足夠大，這樣才能包含足夠充分的孔隙信息，與真實巖心的孔隙結構特征也更相近.姜黎明等(2012)通過代表體積元(REV)方法測試發(fā)現，巖心塊尺寸選在2003時通常能夠包含較豐富的孔隙結構且計算較快，因此本文使用了該尺寸進行子塊分割，之后就可以對子塊巖心進行彈性性質模擬與孔隙網絡提取.

在彈性性質模擬時還需給定巖心中骨架與孔隙部分各自的彈性模量， 那么根據等效介質理論的思想，巖石的等效彈性性質除孔隙結構、孔隙度外，還會受到骨架的礦物組成與巖石飽和流體情況兩個因素的影響.其中碳酸鹽巖的骨架礦物組成較為純凈，常為方解石或白云石.本文樣品經XRD(X-ray diffraction，X射線衍射)礦物分析發(fā)現白云石占90%以上，礦物組成單一，因此在比較所有碳酸鹽巖彈性模量時骨架礦物組成對各樣品實際彈性性質的影響應很小，在此我們給定骨架部分為白云巖的彈性參數(體積模量為80 GPa，剪切模量為58 GPa，該模量通過對同井位中、孔隙度0.1%左右的一非常致密巖心測量得到)；與之相反砂巖骨架的礦物組成通常比較復雜，因此在對比砂巖彈性性質時礦物成分是重要的影響因素，但是考慮到我們的研究核心在于孔隙結構的定量化表征，孔隙結構對彈性性質的影響是我們主要考慮的因素，所以仍舊需要假定巖石骨架礦物成分單一，這樣所有樣品的模擬彈性模量才僅會受到孔隙結構的影響，而不會受不同樣品礦物組成不同所影響.考慮到較純凈的砂巖(如楓丹白露砂巖)基本為石英，本文砂巖經XRD分析石英含量也基本占主導，因此給定砂巖的骨架部分為石英的彈性參數(體積模量為37 GPa，剪切模量為44 GPa；Mavko et al.，1998).同樣為了排除孔隙流體對樣品模擬彈性模量的影響，我們假設兩種巖性樣品的孔隙中都完全飽和空氣.

3 等效孔隙結構定量化表征對比

根據研究思路，我們首先聯合模擬彈性模量與等效介質理論估算等效孔隙縱橫比，以該參數表征數字巖心整體等效的孔隙結構特征.目前已經發(fā)展了多種常用的以孔隙縱橫比來表征孔隙形狀的等效介質模型，它們的假設條件、適用情況以及加入孔隙的方式都有所不同，考慮到計算效率本文使用了較為簡單的顯式MT模型，但是為了對比不同理論計算的等效孔隙縱橫比是否會對孔隙結構表征產生顯著的影響， 我們也給出了DEM模型的計算結果，見附錄B.通過等效孔隙縱橫比分布的對比表明，等效介質理論不同，對最后孔隙結構刻畫造成的影響很小.便于計算的包含N種包裹物的MT模型表示為式(3)(Benveniste，1987)：

(3)

圖9a展示了所有碳酸鹽巖數字巖心模擬縱波速度與孔隙度交會特征，可以發(fā)現交會圖中數據點分布總體比較分散，在孔隙度為10%左右時縱波速度的差異高達2500 m·s-1左右，這只能是不同的孔隙結構引起的；而在砂巖數字巖心模擬縱波速度與孔隙度交會圖中數據點非常集中，呈明顯的近線性分布，同一孔隙度下的縱波速度差距很小，見圖9b.在求取等效孔隙縱橫比時將巖心孔隙度代入式(3)中，計算的等效模量作為輸出，以模擬彈性模量Kmodeling、μmodeling作為約束值作差，構建包含體積模量與剪切模量兩個約束條件下的方程組(4)，通過優(yōu)化算法求解就可以得到當前彈性模量與孔隙度條件下對應的等效孔隙縱橫比.式(4)中OF表示目標函數.

(4)

圖9中每個數據點的顏色代表該點等效孔隙縱橫比，顏色越偏暖色值表示縱橫比值越大，反之縱橫比值越小.圖中藍色虛線表示理論計算的不同等效孔隙縱橫比時縱波速度隨孔隙度變化曲線.在碳酸鹽巖樣品中MT模型計算的等效縱橫比分布在0.03～0.4范圍內，分布區(qū)間比較寬(見頻率直方圖10中紅色所示)，同一孔隙度下都表現為速度越快等效孔隙縱橫比越大，總體上所有數據點可以根據顏色分為下部的冷色值與上部的暖色值兩類；砂巖樣品的等效縱橫比分布在0.2～0.5之間，分布區(qū)間都要小于碳酸鹽巖(見頻率直方圖10中藍色所示)，更加集中.

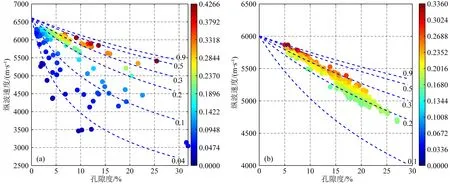
圖9 數字巖心縱波速度-孔隙度交會中等效孔隙縱橫比分布對比(色標表示孔隙縱橫比)(a) 碳酸鹽巖； (b) 砂巖.Fig.9 Distribution of effective pore aspect ratio of digital core in cross-plot between P-velocity and porosity (color represent pore aspect ratio)(a) Carbonate； (b) Sandstone.

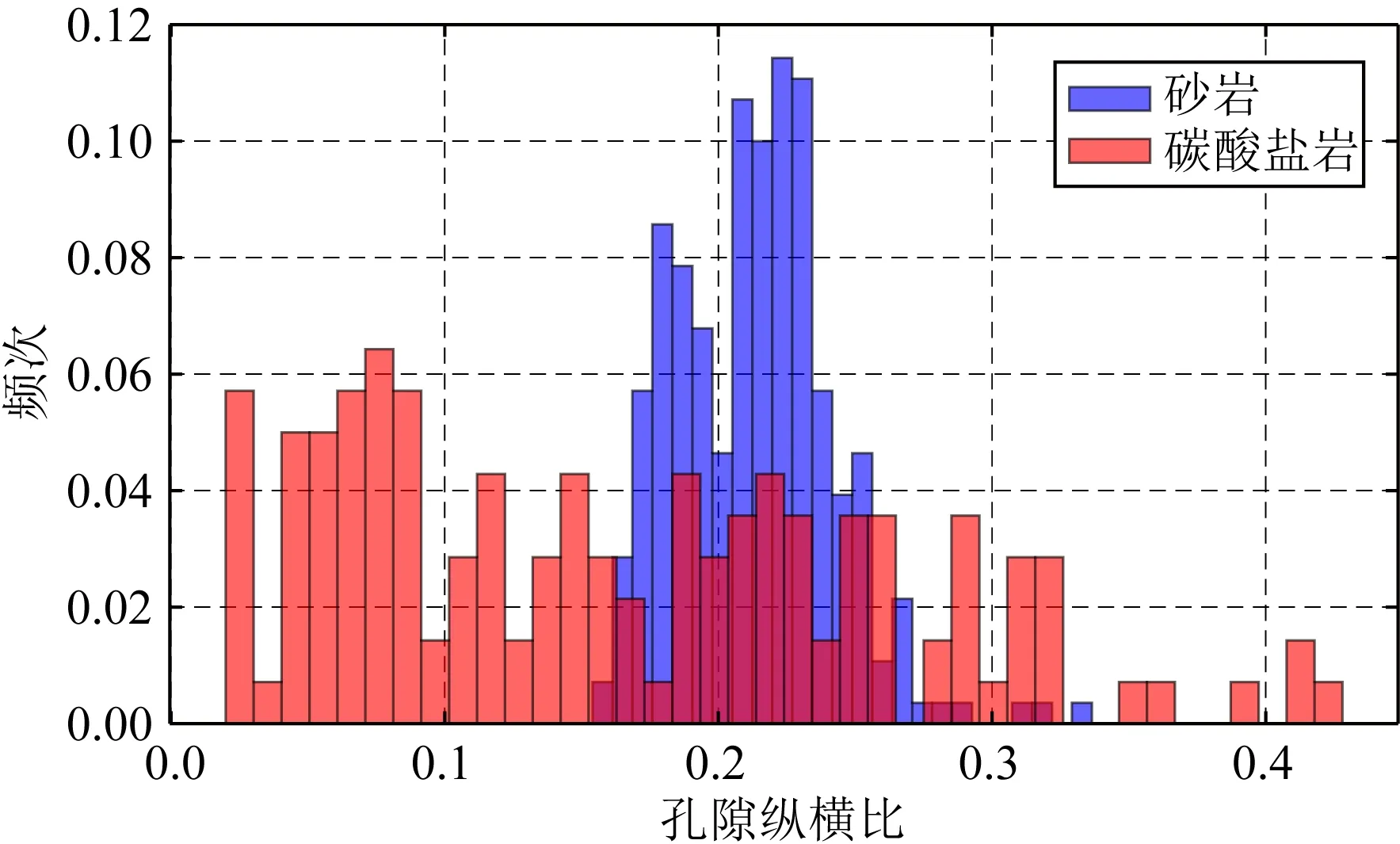
圖10 砂巖與碳酸鹽巖等效孔隙縱橫比頻率分布直方圖Fig.10 Histogram of effective pore aspect ratio in sandstone and carbonate

在使用巖心孔隙網絡模型提取的孔喉參數對孔隙結構進行表征時，考慮到圖4、5中的分析，并且喉道此時更能表現孔隙空間中窄區(qū)域的特征，從而影響孔隙形狀，我們提取了每塊數字巖心所有喉道的平均長度、長度排序后的中間長度、經過喉道體積加權平均的喉道長度和長度分布頻率直方圖峰值4個喉道長度相關的統(tǒng)計性參數作為代表每塊巖心的等效喉道長度，并與等效孔隙縱橫比(基于MT模型計算)進行了交會分析.在圖11中孔喉長度分割系數為0.6時可以明顯發(fā)現碳酸鹽巖的不同喉道長度參數相比砂巖都具有更寬的分布范圍，這種特征和等效孔隙縱橫比的分布特征是一致的；并且碳酸鹽巖各喉道長度參數與等效孔隙縱橫比交會都出現了近似線性趨勢，其中喉道平均長度的相關系數明顯更大、相關性更強，數據分布更集中，表現為縱橫比增大對應喉道長度減小的負相關性.這可以解釋為縱橫比越小的孔隙越呈扁平狀分布，延展更長，因此在提取的孔隙網絡中會有更長的喉道長度，而縱橫比越大的孔隙越接近球體，對應的喉道會縮短.圖12將兩類巖心單獨分析發(fā)現砂巖平均喉道長度與等效孔隙縱橫比交會無明顯相關性，而碳酸鹽巖的交會關系相比圖11c中兩類巖心時基本不變，因此巖性并不會影響兩參數的相關性，圖11c中的交會關系對兩種巖性都是適用的.隨后為了分析孔喉分割系數的影響，我們使用0.4與0.8兩個不同系數重新計算了數字巖心喉道平均長度，并與等效孔隙縱橫比進行了交會分析，見圖13.其中雖然長度值的范圍發(fā)生了變化，但是所有樣品數據點的相對分布規(guī)律并沒有明顯的改變，這表明分割系數對我們的孔隙結構表征研究敏感度較小.根據以上交會分析我們選擇了平均喉道長度作為孔隙結構的表征參數，同樣使用縱波速度與孔隙度做交會，每個數據點顏色表示平均喉道長度值(由于喉道長度非常小，為了便于比較，我們將所有樣品的平均喉道長度以其中的最大值為基準進行了歸一化)，顏色越偏冷色值代表喉道越短，反之喉道越長.孔隙結構表征結果見圖14所示，藍色虛線為MT模型計算的不同等效孔隙縱橫比時縱波速度隨孔隙度變化曲線，作為以喉道長度來定量表征孔隙結構的參考.我們能夠明顯看出圖14中數據點顏色分布與圖9中相似，碳酸鹽巖能夠大致分為喉道較短的冷色點與較長的暖色點兩類，砂巖則都表現為比較單一的喉道長度.

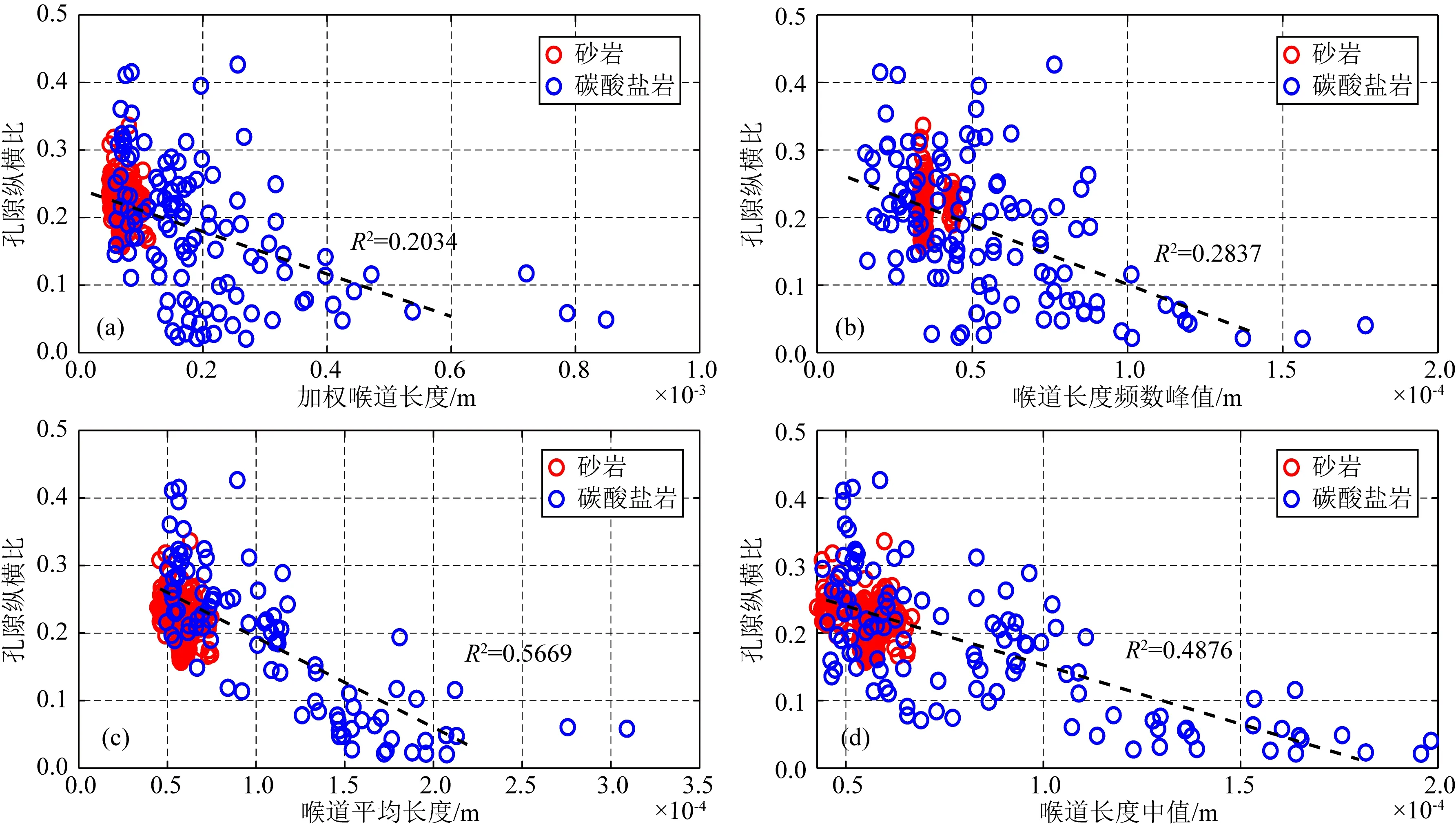
圖11 孔喉長度分割系數0.6時各喉道長度參數-等效孔隙縱橫比交會(a) 加權喉道長度-等效孔隙縱橫比交會； (b) 喉道長度頻率直方圖峰值-等效孔隙縱橫比交會； (c) 喉道平均長度-等效孔隙縱橫比交會； (d) 喉道長度中值-等效孔隙縱橫比交會.Fig.11 Cross-plot between effective pore aspect ratio and parameters which described throat length when pore-throat segmentation coefficient is 0.6(a) Effective pore aspect ratio and weighted throat length； (b) Effective pore aspect ratio and peak value of throat length histogram； (c) Effective pore aspect ratio and average value of throat length； (d) Effective pore aspect ratio and mid-value of throat length.

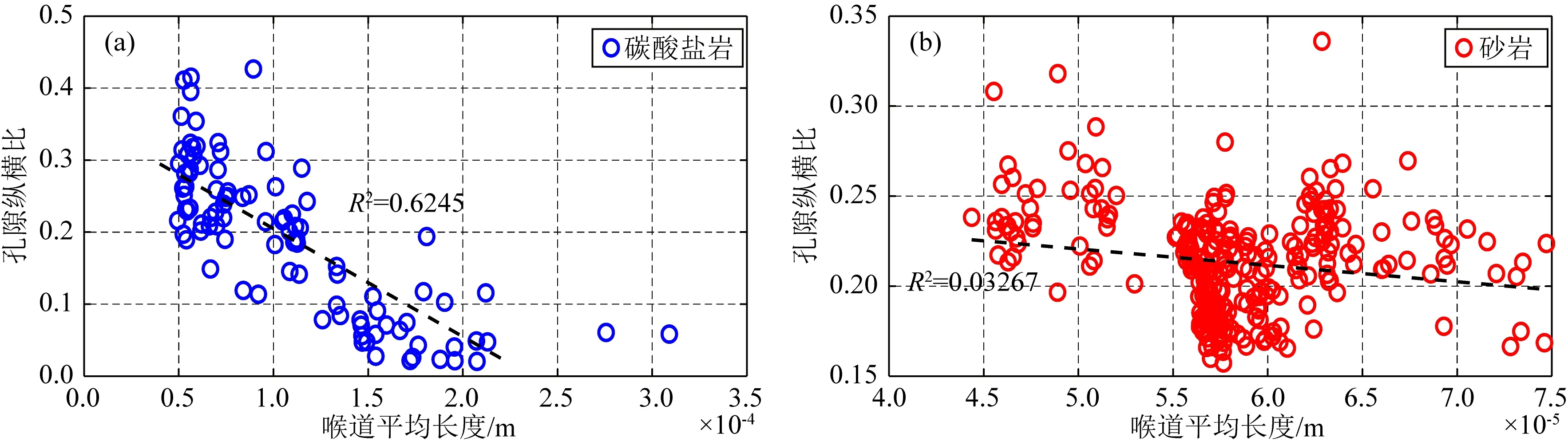
圖12 不同巖心中孔喉長度分割系數0.6時喉道平均長度-等效孔隙縱橫比交會(a) 碳酸鹽巖； (b) 砂巖.Fig.12 Cross-plot between effective pore aspect ratio and average value of throat length when pore-throat segmentation coefficient is 0.6 in different core(a) Carbonate； (b) Sandstone.

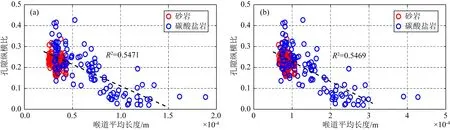
圖13 平均喉道長度-等效孔隙縱橫比交會(a) 孔喉長度分割系數0.4； (b) 孔喉長度分割系數0.8.Fig.13 Cross-plot between effective pore aspect ratio and average value of throat length(a) Pore-throat segmentation coefficient is 0.4；(b) Pore-throat segmentation coefficient is 0.8.

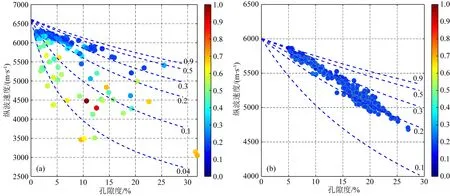
圖14 縱波速度-孔隙度交會圖中數字巖心喉道平均長度分布(色標表示歸一化喉道平均長度)(a) 碳酸鹽巖； (b) 砂巖.Fig.14 Distribution of average length of throat from digital core in cross-plot between P-velocity and porosity (color represent normalized average throat length)(a) Carbonate； (b) Sandstone.

4 討論與誤差分析

經過對以上兩種孔隙結構表征思路結果的對比與分析，證明雖然等效孔隙縱橫比是通過彈性性質這一間接屬性來定量化描述孔隙結構的，但是其對孔隙結構的表征效果與直接從巖心圖像中提取的喉道長度的表征效果是相近的.然而目前我們的巖心樣品中等效孔隙縱橫比與平均喉道長度的交會關系并不是非常理想，因此需要對兩參數可能產生的誤差進行分析.這之中等效孔隙縱橫比由等效介質理論與彈性模量計算得到，其誤差應來自于兩個方面：一個是彈性模擬的結果是否相對準確，另一個則是等效介質理論(MT模型)能否準確描述彈性模量和等效孔隙縱橫比之間的關系.對此我們建立已知孔隙縱橫比的模型介質，通過對比其模擬模量與等效介質理論計算模量間的差距來評估誤差.首先使用位置隨機分布、半徑固定的球體作為孔隙，建立理論上孔隙縱橫比為1的多孔介質；再使用4參數隨機生長法(Quartet Structure Generation Set，QSGS；Wang et al.，2007)，通過控制生長參數生成長軸與短軸比不同的橢球體作為孔隙(同一個模型介質中每個橢球體長短軸都相同)，建立不同孔隙縱橫比的多孔介質，具體的長、短軸長度可以通過對圖像進行測量得到.以上多孔介質不考慮孔隙間的連通性，各個孔隙互不相交，見圖15.

模擬使用石英作為骨架，孔隙中充填空氣.圖16中不同標記點表示模型介質的模擬模量，粉色虛線表示MT模型計算的彈性模量隨孔隙度變化曲線，兩者所用孔隙縱橫比互相對應.對比發(fā)現兩模量相差較小，這表明對于簡單的、孔隙結構單一且分布均勻的多孔介質，彈性模擬結果是可靠的，等效介質理論也基本能準確計算彈性模量.但是在孔隙結構復雜時等效介質理論的誤差很難評價，這是因為很難像圖15中的簡單模型一樣通過測量孔隙長短軸定量化提取復雜孔隙的等效縱橫比，而只能由彈性模量反演計算一個理論值.因此裂縫型孔隙定向排列引起的各向異性、孔隙位置與區(qū)域的非均勻分布都可能使巖石不滿足等效介質理論的假設，從而使等效孔隙縱橫比無法反映真實的孔隙結構特征，導致圖11c中的擬合誤差.另外等效孔隙縱橫比也無法反映孔隙之間的聯通特性，忽略了孔隙結構對滲流性質的影響.

喉道長度參數的誤差主要來源于從孔隙空間提取孔隙網絡的過程.通過圖2對一球體顆粒堆積形成的簡單孔隙空間提取孔隙網絡后發(fā)現，雖然最大球法對孔隙空間中局部寬區(qū)域的孔隙與局部窄區(qū)域的喉道有明確的定義方法，但是對兩者中間剩余空間的歸屬還是比較模糊的，這也就導致了確定的喉道長度與孔隙長度可能并不準確.在上文中我們分析了最大球法分割孔喉時分割系數對喉道長度的影響，發(fā)現該參數基本只會影響喉道長度值的整體范圍，對所用樣品喉道長度分布的相對趨勢與規(guī)律性沒有影響.但是孔隙網絡最開始是以研究滲流特性為目的而展開的，為了簡便而將孔隙空間轉化為孔隙網絡，并認為孔隙網絡能夠近似代替實際的孔隙空間，這種近似可能不會對滲流特性產生明顯影響，但是對原本孔隙結構的表征肯定存在誤差；此外網絡模型也相當于將原本聯通在一起的孔隙空間分割開來，即使分割過程有最大球法作為理論依據，分割的位置也可能會對實際孔隙結構的刻畫產生影響，這些因素都可能導致同一喉道長度下出現多個等效孔隙縱橫比，使兩者間的關系出現誤差.因此在分析等效孔隙縱橫比定量化表征復雜孔隙結構的誤差方面，我們對彈性模擬、圖像形狀的定量化表征、孔隙網絡提取及孔喉分割還需要更多的研究和嘗試，對于孔隙結構復雜、非均質性強的碳酸鹽巖也需要更多的研究樣品，才能獲得更加可靠的等效孔隙縱橫比與平均喉道長度間的經驗關系.

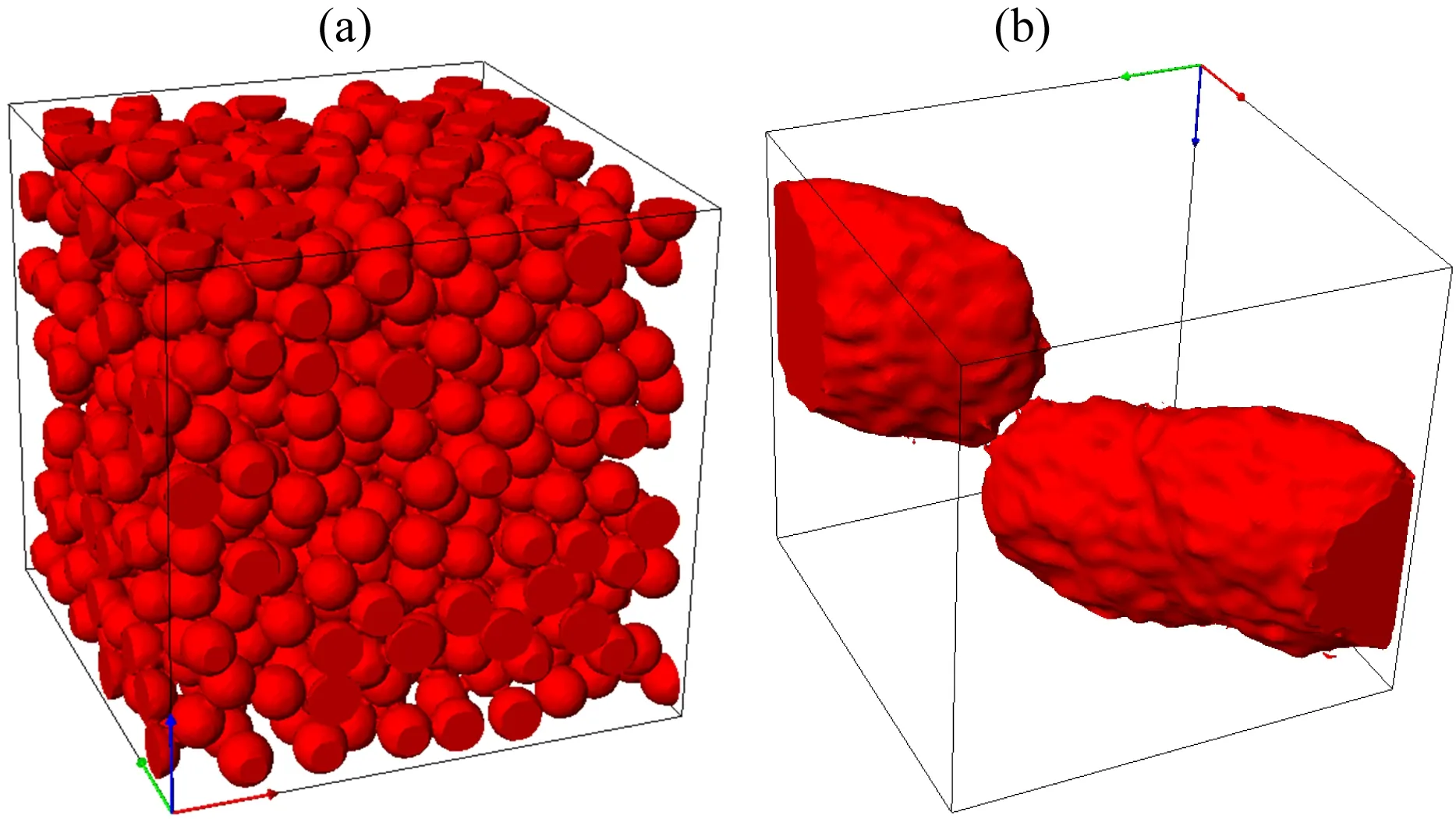
圖15 不同單一孔隙縱橫比模型(a) 球狀孔隙模型，孔隙縱橫比為1； (b) 橢球狀孔隙模型， 控制孔隙縱橫比定量變化.Fig.15 Model in different single pore aspect ratio(a) Sphere pore model, pore aspect ratio is 1； (b) Ellipsoid pore model, pore aspect ratio is designed quantitatively.

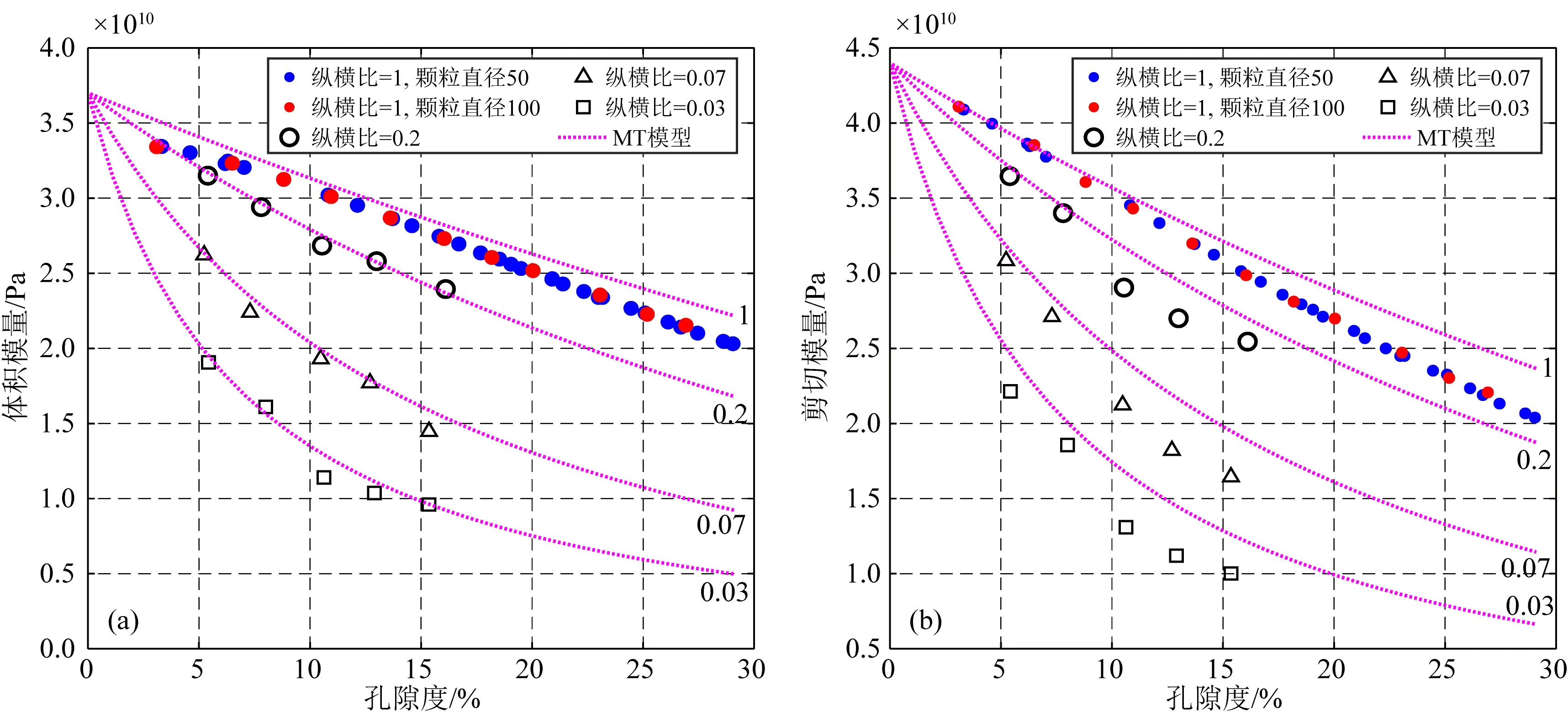
圖16 不同單一孔隙縱橫比模型模擬彈性模量與等效介質理論計算模量對比(圖中不同符號點代表 不同單一孔隙縱橫比模型的模擬模量，虛線為MT模型計算模量，數字為對應孔隙縱橫比)(a) 體積模量； (b) 剪切模量.Fig.16 Comparison of simulated elastic modulus with calculated modulus by effective medium theory for different single pore aspect ratio model (Different symbolic points represent the simulated modulus of different single pore aspect ratio models, the dotted line represents calculated modulus by MT model, and the number represents the corresponding pore aspect ratio)(a) Bulk modulus； (b) Shear modulus.

5 結論與展望

本文從兩種不同角度出發(fā)獲取巖石孔隙結構特征的表征與描述結果，并對比了兩種方法對孔隙結構進行表征的相似性.其中，基于彈性性質并結合等效介質理論計算等效孔隙縱橫比的方法是目前最常用的孔隙結構描述方法，在地震以及測井數據的孔隙結構預測上已有比較多的應用，該方法并不是直接從孔隙空間的幾何特征中求得孔隙結構參數，而是通過等效介質理論將這種幾何特征間接與巖石彈性性質聯系了起來.本研究中，借助于數字巖心可以提取儲層巖石的孔隙網絡模型，并由此出發(fā)提取具有明確地質意義的喉道長度，作為表征孔隙結構的幾何參數.我們的研究發(fā)現，彈性性質聯合等效介質理論估算的等效孔隙縱橫比參數與直接從數字巖心提取的喉道長度這一幾何參數，二者具有很好的相關性，喉道長度長對應于等效孔隙縱橫比小的扁平裂縫型孔隙，反之對應于等效孔隙縱橫比大的球形孔洞型孔隙.本研究在一定程度上強有力地證明，彈性性質聯合等效介質理論這種間接反演等效孔隙縱橫比的思路，對形狀復雜的孔隙結構進行定量化表征具有準確性與合理性.相比在地震或測井孔隙結構預測時，僅使用成像測井、少量巖心薄片或橫波預測誤差等來驗證等效孔隙縱橫比對孔隙結構描述的效果，本文提供了更加定量化、更加直接的證據.此外，由于等效孔隙縱橫比參數與喉道長度之間良好的相關性，而喉道特征通常是描述儲層滲流特性的重要參數，這使得將基于測井數據或地震數據預測的等效孔隙縱橫比屬性體轉化為更具開發(fā)價值的滲流屬性體成為可能.

附錄A

對于孔隙縱橫比α小于1的極化因子，可以表示為(Mavko et al.，1998)：

式中，(Km,Gm)為骨架的彈性模量；(Ki,Gi)為孔隙包含物的彈性模量；α為孔隙縱橫比.

附錄B

包含N種孔隙的DEM模型可以表示為微分方程式(B1)(Berryman et al.，2002)：

(B1)

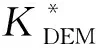
圖B1與圖B2中每個數據點的顏色代表該點孔隙縱橫比，顏色越偏暖色值表示縱橫比值越大，反之縱橫比值越小，圖中藍色虛線表示理論計算的不同孔隙縱橫比時縱波速度隨孔隙度變化曲線.對比發(fā)現不同理論計算的結果有所區(qū)別，DEM模型計算的孔隙縱橫比較MT模型偏大一些，但是不同巖性孔隙縱橫比的分布特征是一致的.在碳酸鹽巖樣品中DEM模型計算的孔隙縱橫比分布在0.04～0.5范圍內，MT模型計算的縱橫比分布在0.03～0.4范圍內，不同模型的孔隙縱橫比分布區(qū)間都比較寬(見頻率直方圖B3a、b中紅色所示)，同一孔隙度下都表現為速度越快孔隙縱橫比越大，總體上所有數據點可以根據顏色分為下部的冷色值與上部的暖色值兩類；砂巖樣品DEM模型計算的縱橫比在0.3～0.5之間，MT模型則在0.2～0.5之間，不同模型孔隙縱橫比的分布區(qū)間都要小于碳酸鹽巖的分布區(qū)間且縱橫比整體較大(見頻率直方圖B3a、b中藍色所示)，從顏色上所有的數據點都為暖色，沒有明顯的冷色值.以上對比表明即使使用的等效介質理論不同，也不會對孔隙縱橫比的計算及最后對孔隙結構的表征產生顯著影響.

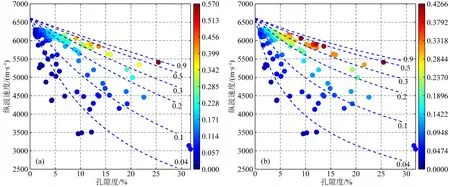
圖B1 縱波速度-孔隙度交會圖中碳酸鹽巖數字巖心等效孔隙縱橫比分布(色標表示孔隙縱橫比)(a) 基于DEM模型； (b) 基于MT模型.Fig.B1 Distribution of effective pore aspect ratio of carbonate digital core in cross-plot between P-velocity and porosity (color represent pore aspect ratio)(a) Calculated by DEM model； (b) Calculated by MT model.

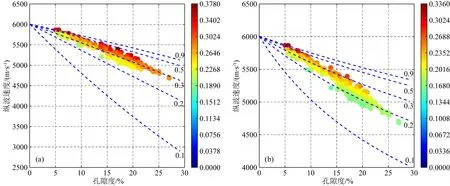
圖B2 縱波速度-孔隙度交會圖中砂巖數字巖心等效孔隙縱橫比分布(色標表示孔隙縱橫比)(a) 基于DEM模型； (b) 基于MT模型.Fig.B2 Distribution of effective pore aspect ratio of sandstone digital core in cross-plot between P-velocity and porosity (color represent pore aspect ratio)(a) Calculated by DEM model； (b) Calculated by MT model.

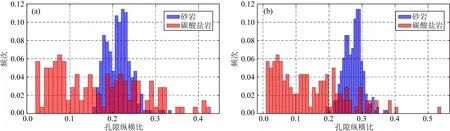
圖B3 砂巖與碳酸鹽巖等效孔隙縱橫比頻率分布直方圖(a) MT模型計算； (b) DEM模型計算.Fig.B3 Histogram of effective pore aspect ratio in sandstone and carbonate(a) Calculated by MT model； (b) Calculated by DEM model.