“做”中感悟推理論證
文/王競進

第2章軸對稱圖形
組稿團隊:江蘇省建湖縣王競進初中數學名師工作室
領銜人:王競進(正高級教師)
“軸對稱圖形”是蘇科版數學八(上)第2章的內容。在小學階段,我們已經了解了線段、角,認識了等腰三角形、等邊三角形,進入初中后,還學習了平行線、全等三角形,掌握了它們的概念、性質和應用,并發展了我們的思考和表達能力。對于本章內容,我們該如何進行學習呢?接下來,我們來一起了解本章學習的整體思路,以期幫助同學們構建完整的知識結構。
一、在“做”中感悟概念
本章的內容包括軸對稱與軸對稱圖形、軸對稱的性質、設計軸對稱圖案、線段與角的軸對稱性以及等腰三角形的軸對稱性,需要同學們親自體會、認識并概括出它們的概念和基本性質。比如,線段是軸對稱圖形,同學們往往不借助實踐操作,以為它的對稱軸只有這條線段的垂直平分線,但通過動手操作,就會發現,它還有另外一條對稱軸,就是這條線段所在的直線;又如,我們沿著等腰三角形ABC(如圖1)頂角的角平分線AD進行折疊,發現△ABD、△ACD是能夠完全重合的,進而猜想、概括等腰三角形的性質。

圖1
同學們在“做”的過程中,逐漸領悟本章的這些知識點。從知識結構上來看,它們之間也是密切聯系、相輔相成的,是一個完整的、有機的整體。其關系可以用圖2表示,彰顯出數學素養的要求,讓我們從生活中的軸對稱現象抽象出生活中的軸對稱或軸對稱圖形,也使得我們經歷了從特殊到一般的過程,感受類比思想和方法。

圖2
二、在論證中培養推理能力
教材在本章還安排了折紙、畫圖、猜想等多種形式的數學活動,讓我們感受到軸對稱圖形的數學本質。在經歷實踐操作、猜想的過程中,我們進行驗證和恰當的數學分析,證明自己發現的結論是正確的,從而培養發現問題、提出問題、分析問題和解決問題的能力以及邏輯推理能力。
例如,對于上述等腰三角形的性質,應用全等三角形的條件與性質進行如下的推理與證明。
如圖1,因為AD=AD,∠BAD=∠CAD,AB=AC,所以△ABD≌△ACD(SAS),所以∠B=∠C,BD=CD。
三、在一題多解中提升思維品質
等腰三角形的判定條件“有兩個角相等的三角形是等腰三角形”,也就是如圖3,在△ABC中,∠B=∠C。那么,我們如何證明AB=AC呢?
圖3
如圖4,我們可以作∠BAC的角平分線AD,也可以作中線AD,還可以作高線AD,都能夠得到△ABD≌△ACD,進而得到AB=AC。其實,我們還可以根據其他三角形全等,證明AB=AC。如圖3,∠C=∠B,BC=CB,∠B=∠C,所以△ABC≌△ACB,所以AB=AC。
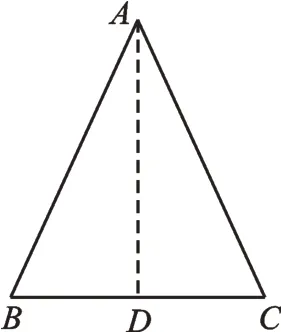
圖4

無論是在研究平行線的性質與條件、全等三角形的性質與條件,還是研究本章學習的軸對稱圖形的性質與條件時,我們都要能夠在“做”數學的過程中感悟方法、學會推理論證,養成善于思考、樂于反思的好習慣,不斷提升自己的思維品質。

