合理分類有序轉化
文/何平
“對稱圖形——圓”這一章涉及的數學思想方法很多,老師將和大家一起來學習圓中的分類思想和轉化思想。
我們在解決圓中有關計算問題時,通過對條件進行分析,發現條件和結論不確定時,往往需要分類討論。通過尋找分類的對象和明確分類的標準,我們可以做到不重復、不遺漏地得出答案,從而全面地思考問題,讓思維更加縝密。
例1在⊙O中,弦AB所對圓心角為70°,則弦AB所對的圓周角為___。
【分析】因為題目中弦AB所對的圓周角位置不確定,所以需要分類。分類的對象是圓周角,分類的情況是圓周角的頂點在弦AB所對的兩條弧上。
解:如圖1,當點P1在︵上時,

圖1
∵∠AOB=70°,∴∠AP1B=35°。
當點P2在上時,
∵∠AOB=70°,

因此,弦AB所對的圓周角是35°或145°。
例2已知⊙O直徑CD與弦AB垂直,垂足為H,若AB=6,CD=10,則AC=___。
【分析】因為題目中弦AB的位置不確定,所以需要分類。分類的對象是弦AB,分類的情況是弦AB在圓心的兩側。
解:如圖2,連接OA。

圖2
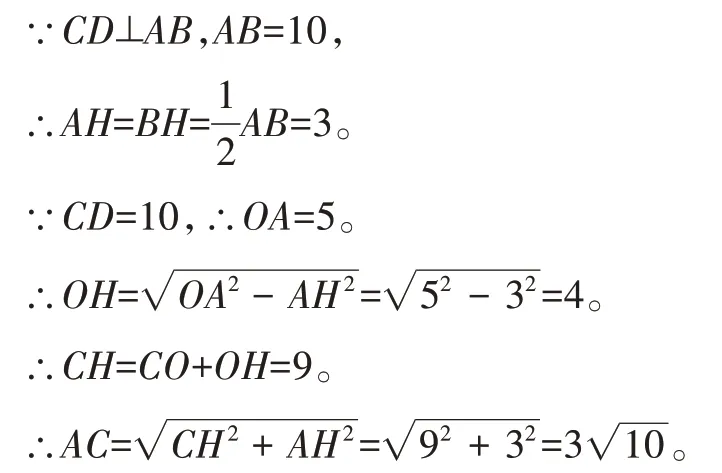
如圖3,CH=CO-OH=1,

圖3

因此,AC=3或。
【點評】通過這兩道例題,我們可以發現,分類思想蘊含在最基本的點、直線、角與圓的位置關系等圖形中,常見的有圓周角的分類、弦的位置分類等。總之,當問題中條件或結論中的相關量不確定時,就要明確分類方法,合理進行分類討論。
轉化思想在圓這一章中同樣被廣泛地運用在計算與證明中。對于圓中的相關問題,通過對條件與結論的分析,借助最近聯想,適當添加輔助線,可以將圓中較為復雜的圖形逐步分解成同學們熟悉的基本圖形,從而實現對復雜問題的轉化。
在同圓或等圓中,由弦相等得弧相等
例3如圖4,在⊙O中,弦AB、CD相交于點P,若AB=CD。求證PB=PD。

圖4
【分析】要證明兩邊相等,通常可以借助三角形全等或者“等角對等邊”等方法來解決。觀察圖形,容易聯想到連接BD,再證明∠B=∠D即可。
證明:如圖5,連接BD。

圖5

【點評】本題從結論出發,尋找結論與條件之間的聯系,將條件中的相等的弦轉化為對應的弧相等,從而得到對應的圓周角相等。解決問題時,我們只有樹立將同圓或等圓中的圓心角、弧、弦三者之間的關系進行有序轉化的意識,才可以優化解題過程。
圓中內接多邊形的轉化
例4如圖6,在⊙O的內接六邊形ABCDEF中,∠A+∠C=220°,則∠E=°。

圖6
【分析】本題是圓內接六邊形的角度計算,只要添加輔助線BE即可將圓內接六邊形轉化為圓的兩個內接四邊形。
解:如圖7,連接BE。

圖7
∵四邊形ABEF是⊙O的內接四邊形,
∴∠A+∠BEF=180°。
同理,∠C+∠BED=180°。
∴∠A+∠BEF+∠C+∠BED=360°。
又∵∠A+∠C=220°,
∴∠BEF+∠BED=360°-220°=140°。
∴∠E=140°。
【點評】對于圓內接多邊形中角度的計算問題,我們需要添加適當的輔助線將復雜的圖形轉化為圓的內接四邊形或者三角形。因此,轉化是解決此類問題的關鍵。
圓中陰影部分面積的轉化
例5如圖8,圓形時鐘的半徑為2,其中每個刻度間的弧長均相等,過9點和11點的位置作一條線段,則鐘面中陰影部分的面積為____。
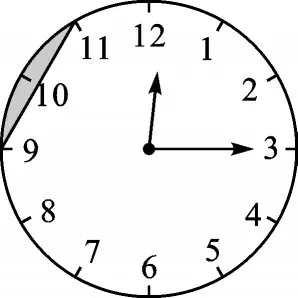
圖8
【分析】通過連接半徑,可以將陰影部分面積轉化為扇形AOB的面積與△AOB的面積之差。
解:連接OA、OB,過點O作OC⊥AB于點C,由題意可知∠AOB=60°。

圖9
∵OA=OB,∴△AOB為等邊三角形。
∴AB=AO=BO=2。
∵AO=BO,OC⊥AB,
∴∠OCA=90°,AC=1。∴OC=。

又∵
∴陰影部分的面積為
【點評】對于陰影部分面積的計算,我們通常將不規則的圖形進行分解,轉化為與之相關聯的規則圖形后再進行計算。正確添加輔助線,可以將圖形進行有效的轉化。

