固本思“源”無中生“圓”

文／王進

教材的例題是學習之“源”，部分中考題實際上就是在教材例題或習題的基礎上，進行組合、加工、深化得到的。因此，同學們要重視自己的學習過程，對教材中的例題變式或習題變式多加思考，以鍛煉自己的數(shù)學思維能力。下面以蘇科版數(shù)學教材九年級上冊第57頁的例2為模板，談談例題的學習與拓展。

【原題呈現(xiàn)】如圖1，AB是⊙O的直徑，弦CD交AB于點E，∠ACD=60°，∠ADC=50°。求∠CEB的度數(shù)。

圖1

【分析】本題要想求∠CEB的度數(shù)，從原圖上來看似乎只能借助對頂角、鄰補角或三角形的外角來解決，但這三種思路無法與“∠ADC=50°”建立實質性的關聯(lián)，所以想到作輔助線。由條件“AB是⊙O的直徑”聯(lián)想到構造直徑所對的圓周角，所以連接BD得到△BDE，再借助外角的性質定理即可求出“∠CEB=∠ABD+∠EDB”。此時只剩下∠ABD一個未知量，利用“同弧所對的圓周角相等”即可化未知為已知。輔助線也可以連接BC，再借助三角形內角和定理求出∠CEB的度數(shù)。

本題在連接BD后，構造出了直角、同弧所對的圓周角以及△BDE。通過輔助線構造新的角是幾何證明常見的方法之一，而輔助線的選擇往往和題目中的已知條件和未知的結論相關，由“已知”想“可知”，由“未知”推“需知”，從兩頭出發(fā)，向中間靠攏，最終選擇最優(yōu)輔助線。

變式1（2019·江蘇南京）如圖2，⊙O的弦AB、CD的延長線相交于點P，且AB=CD。求證：PA=PC。

圖2

【分析】想要證明兩條線段相等，如果將其分別放在兩個三角形中，首先想到證明“兩個三角形全等”；如果將其放在一個三角形中，首先想到利用“等角對等邊”證明這個三角形是等腰三角形。通過比較，發(fā)現(xiàn)連接AC構造△APC更為簡便，再利用“等弧所對的圓周角相等”即可證明△APC為等腰三角形。

證明：連接AC。

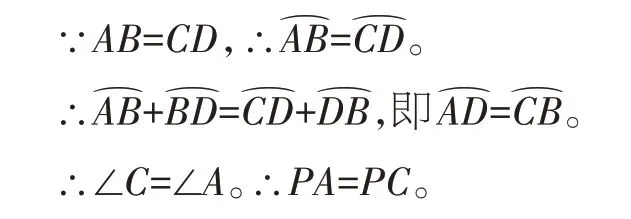
【點評】“全等”“等角對等邊”是證明兩邊相等的兩種常見方法。而在圓中，我們需要利用“同弧或等弧所對的圓周角相等”來找到具有相等關系的角，從而掌握更為簡便的證明方法。

變式2（2022·新疆）如圖3，⊙O是△ABC的外接圓，AB是⊙O的直徑，點D在⊙O上，AC=CD，連接AD，延長DB交過點C的切線于點E。求證：BE⊥CE。

圖3

【分析】對于這類題型，我們應利用好圓的性質，抓住“同弧或等弧所對的圓周角相等”“圓內接四邊形的對角互補”等關鍵信息，尋找相等關系的角。從位置關系想數(shù)量關系，從數(shù)量關系想位置關系，做好“數(shù)量關系”與“位置關系”之間的轉化。

證明：連接OC。

∵CE與⊙O相切于點C，∴∠OCE=90°。

∵AC=CD，∴∠ADC=∠CAD。

∴∠CAD=∠ABC。

∵四邊形ADBC是圓內接四邊形，

∴∠CAD+∠DBC=180°。

又∵∠DBC+∠CBE=180°，

∴∠CAD=∠CBE。

又∵∠ABC=∠CAD，∴∠ABC=∠CBE。

∵OB=OC，∴∠ABC=∠OCB。

∴∠CBE=∠OCB。∴OC∥BE。

∴∠OCE+∠E=180°。

∴∠E=180°-∠OCE=180°-90°=90°。

∴BE⊥CE。

【點評】本題重在考查同學們對圓的性質的靈活運用。我們在熟悉教材例題的同時，也要經常思考如何才能巧妙地架起多個知識點間的橋梁，如何選擇和串聯(lián)好不同的定理，只有在不斷的反思與總結中才能做到熟能生巧。

變式3如圖4，已知等腰梯形ABCD中，AD∥BC，點P是梯形外一點，PD與底邊BC相交于E，若PA=PC，∠APC=∠BCD，求證：PB=PE。

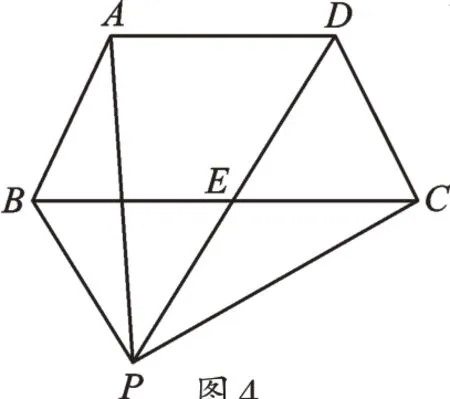
圖4

【分析】引入四邊形的外接圓，通過證四點共圓，證五點共圓，將圖形放在同一個圓中處理，利用“同圓中，同弧或等弧所對的圓周角相等”從而使問題得到順利解決。

證明：∵四邊形ABCD是等腰梯形，

∴∠ABC=∠DCB，AB=CD。

∵AD∥BC，

∴∠ABC+∠BAD=180°，∠DCB+∠ADC=180°。

又∵∠ABC=∠DCB，

∴∠ABC+∠ADC=180°，∠DCB+∠BAD=180°。

∴點A、B、C、D四點共圓。

∵∠APC=∠BCD，∠DCB+∠ADC=180°，

∴∠APC+∠ADC=180°。

∴點A、P、C、D四點共圓。

∴點A、B、P、C、D五點共圓。

∴∠BAP=∠ECP。

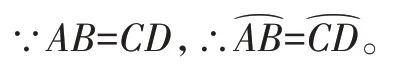
∴∠APB=∠CPE。

在△ABP和△CEP中，

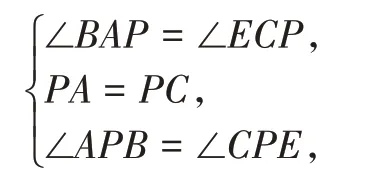
∴△ABP≌△CEP（ASA）。

∴PB=PE。

【點評】借助“對角互補的四邊形的四個頂點共圓”構造出“輔助圓”，再利用“同圓中，同弧或等弧所對的圓周角相等”將看似無關的兩個角建立起等量關系，最后利用“三角形全等”得證。

變式4（2017·廣西河池）如圖5，在矩形ABCD中，AB=，E是BC的中點，AE⊥BD于點F，則CF的長是____。

圖5

【分析】如圖6，連接DE，首先因為E是矩形ABCD邊BC的中點，由矩形的對稱性可知DE=AE，所以Rt△ABE和Rt△DCE的外接圓是等圓（直徑AE=DE）。因為∠EFD+∠DCE=90°+90°=180°，所以點D、F、E、C四點共圓。由“圓的內接四邊形的外角等于內對角”可知∠AEB=∠CDF，即得到兩等圓中的等角。最后，通過“等角對等弦”即可求出CF=AB=2。

圖6

【點評】“同圓中，同弧或等弧所對的圓周角相等”是我們經常使用的圓的性質定理，但其實，在等圓中也同樣適用。在常規(guī)的幾何圖形中構造等圓是本題的一個妙解，用“等角對等弦”來解決，新穎別致，簡潔明了。

許多同學在圓的學習中都會通過添加垂線段、連接圓心與圓上一點形成半徑或連接圓上兩點形成直徑等進行解題，這類方法可以解決部分題型的變式，但在解決一些較難問題時，上述方法就起不了太大作用。例如，在上述變式3和變式4中，題目中本身沒有圓，但往往只需要在圖形中構造“輔助圓”，根據圓的相關性質，就能使問題化難為易。