考慮時空擁堵和時間窗的多配送中心路徑優化
陳沿伊,侯華保
(武漢理工大學 交通學院,武漢 430070)
0 引 言
由于生鮮產品的易腐性特征,生鮮配送過程中,客戶滿意度不僅受客戶預約時間的影響,還受生鮮產品保鮮期長短及配送時間等因素的影響。當前關于生鮮配送的研究主要考慮商品保鮮期,綜合考慮多種不確定因素的研究較少。
梁承姬等[1]為提高生鮮配送的時效性,考慮待配送客戶時間窗,以實現配送過程中成本最小且客戶滿意度最大;王恒等[2]研究生鮮配送時間不確定情況下配送時效性的問題,考慮客戶時間窗及道路實際特征,建立了生鮮配送路徑優化模型;李暢等[3]研究生鮮配送的時效性問題時,考慮生鮮產品易腐性,建立以商品新鮮度最大和配送成本最低的多目標生鮮配送路徑優化模型;吳欣[4]、張濟風等[5]在研究配送時間不確定背景下的生鮮配送問題時,考慮配送過程中配送速度的時變性;康凱等[6]以碳排放最低為目標,研究了考慮客戶時間窗的冷鏈配送問題,建立了考慮碳排放的生鮮配送模型。但是,上述研究主要研究配送時效性或配送時間的不確定性,綜合考慮二者的研究較少,且生鮮配送的時效性影響因素較多。當前關于生鮮配送時效性的研究,影響因素考慮得不全面,且當前研究多配送中心下的生鮮配送問題較少,不符合當下生鮮配送多配送中心化的趨勢。
關于路徑優化的求解方法,張建勇等[7]結合聚類思想與遺傳算法,提出混合遺傳算法,解決帶模糊時間窗的多對多車輛路徑問題;S.HUBER等[8]采用變鄰域搜索的方式解決路徑優化問題;胡蓉等[9]設置多種鄰域操作及局部優化模型,嵌入蟻群算法,解決考慮速度空間特征的車輛路徑問題;邵倩[10]將遺傳算法引入非支配算子,求解考慮速度空間特征帶模糊時間窗的物流配送問題;S.IQBAL等[11]利用人工蜂群算法,結合局部鄰域搜索優化,解決帶軟時間窗的車輛路徑問題;B.D.SONG等[12]提出基于優先級的啟發式(PBH)算法進行求解單目標車輛路徑問題;范厚明等[13]基于擂臺賽法構造非支配解,將局部優化算子引入遺傳算法,解決多目標車輛路徑問題;周鮮成等[14]在蟻群算法中設計確定性和隨機性結合的轉移策略;趙志學等[15]結合模型特點,在蟻群算法中引入約束算子,緩解了復雜問題易陷入局部最優的問題;張得志等[16]采用遺傳算法解決考慮速度時變特征的路徑優化問題;M.ALZAQEBAH等[17]采用改進人工蜂群算法解決帶時間窗的車輛路徑問題。
綜上所述,當前關于生鮮配送的研究主要以單配送中心為主,考慮多配送中心的研究較少,不能適應當前生鮮電商配送多配送中心化的發展趨勢。另外,當前研究綜合考慮時間窗、保鮮期、路網擁堵特征的研究較少,研究結果不能完全反映配送的實際情況。鑒于此,筆者建立綜合考慮客戶時間窗、商品保鮮期和路網擁堵特征的多配送中心生鮮路徑優化模型。因模型的復雜性較高,筆者在傳統蟻群-遺傳算法的基礎上,采用兩邊逐次修正算法對初始種群進行局部優化,對種群適應度值降序排列后,選擇前30%作為精英個體,利用蟻群-遺傳算法進行迭代優化,并對算法參數進行正交試驗設計,優化算法參數。基于上述操作,可以有效改善算法搜索空間及求解質量。最后以多種分布特征的Solomon算例和筆者提出的算法為基礎,將該模型與不考慮商品保鮮期和不考慮客戶時間窗的模型計算結果進行對比,以驗證該模型可以在配送時間不確定情況下有效提升配送的時效性,并將筆者提出的算法與傳統算法進行對比,驗證算法有效性。
1 模型描述
1.1 模型描述
某生鮮企業在該區域有多個配送中心,每個配送中心存在多種車型。現需要對該區域的客戶訂單進行配送,需盡量滿足客戶預約時間要求且維持商品新鮮度,以保證客戶滿意度。考慮到車輛行駛速度受高峰小時及所處位置的影響和客戶滿意度受客戶時間窗及商品保鮮期的影響,筆者提出速度時空擁堵函數和綜合模糊時間窗,建立時空擁堵下考慮客戶時間窗和商品保鮮期的多車場多車型生鮮配送路徑優化模型。
1.2 模型參數與假設
1.2.1 模型參數
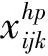
1.2.2 模型假設
模型假設如下:①該區域有多個配送中心,每個配送中心有多種車型,車輛數足夠;②每個客戶僅被一輛車一次服務;③車輛行駛速度受時間和空間的影響;④每輛車服務結束后返回原車場;⑤車輛晚于商品保鮮期到達,客戶滿意度為0;⑥配送速度不能超過最大允許速度。
1.3 模型建立
1.3.1 客戶滿意度函數
1)客戶模糊時間窗
基于客戶模糊時間窗,貨物在時間區間[Li,Ui]內送達,客戶滿意度為1;在[li,ui]區間外到達客戶滿意度為0,其他區間客戶滿意度處于遞增或遞減狀態,具體見圖1。
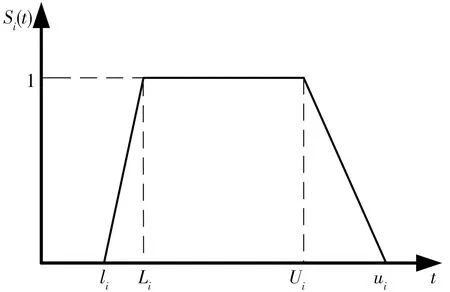
圖1 客戶滿意度函數
2)商品保鮮期
假設在商品保鮮期前送達客戶滿意度為1,超過商品保鮮期,客戶滿意度為0,詳見圖2。
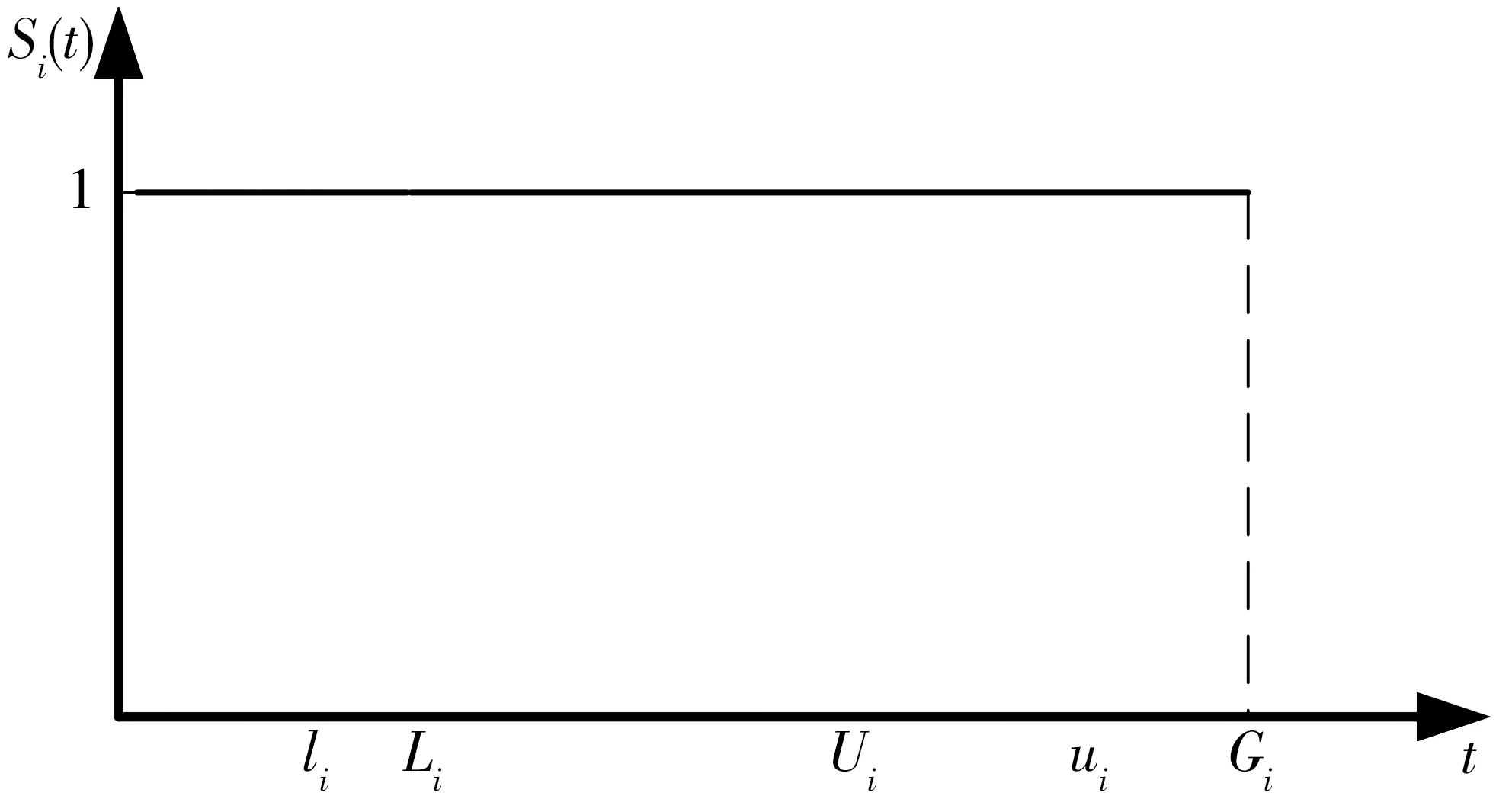
圖2 商品保鮮期
3)綜合模糊時間窗下客戶滿意度函數
綜合考慮客戶時間窗和商品保鮮期,取客戶時間窗和商品保鮮期交集,以反映客戶時間窗和商品保鮮期共同作用下的客戶滿意度隨時間的變化情況。假設當商品超過保鮮期送達時,客戶滿意度為0,當在客戶時間窗和商品保鮮期之間送達,滿意度變化服從客戶時間窗下的滿意度對應法則。綜上所述,建立綜合模糊時間窗下的客戶滿意度函數,見圖3。圖3(a)~圖3(d)滿意度關系式分別對應式(1)~式(4)。
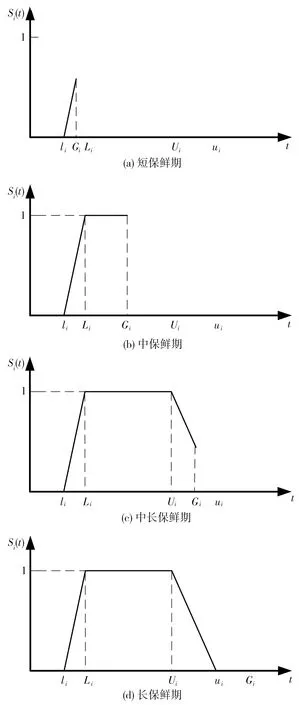
圖3 綜合模糊時間窗下客戶滿意度函數
(1)
(2)
(3)
(4)
1.3.2 速度時空函數
1)速度時間擁堵系數
速度時間擁堵系數反映了不同時刻的路網擁堵特征。高峰小時附近,路網較為擁堵;其他時間,路網交通流較少,擁堵程度降低,見式(5):
(5)
2)速度空間擁堵系數
配送速度受空間因素制約。郊區配送速度高于市區配送速度;距離區域中心越遠配送速度越大。空間擁堵系數計算方法見式(6):
(6)
3)速度時空函數
綜合考慮速度的時間和空間因素及道路最大限度vmax、道路最低時速vmin等因素,建立速度時空演變函數,見式(7):
(7)
1.3.3 目標函數去量綱處理
1)車輛使用數、配送距離、客戶平均滿意度處理分別如式(8)~式(10):
(8)
(9)
(10)
2)多目標加權處理
筆者采用加權法將多目標轉化為單目標,權重由專家打分確定,各個目標通過去量綱化,消除單位對加權后目標值的影響。去量綱化方法見式(11)~式(14):
(11)
式中:maxf1、minf1分別表示當次迭代中種群最多和最少車輛使用數。
(12)
將客戶平均滿意度與1做差,使得各目標協同,max(1-f3)、min(1-f3)分別表示做差后的當次迭代種群內的極值。
(13)
經過專家打分,確定車輛使用數、配送里程、客戶平均滿意度的權重分別為0.22、0.47,0.31,對各個子目標加權處理得到總體目標值:
(14)
1.3.4 模型與約束
模型與約束見式(15)~式(25):
(15)
(16)
(17)
(18)
(19)
(20)
?k∈HP,?S∈J)
(21)
?j∈V)
(22)
(23)
(24)
(25)
其中,式(15)表示加權后的目標值;式(16)表示每個客戶由且僅由一輛車務;式(17)表示車輛服務完一個客戶后會返回車場或前往下一個客戶;式(18)表示車輛行駛距離不應超過其規定最大行程;式(19)表示任何從車場出發的車輛最終返原車場;式(20)表示任意一輛車的載重不可超過其額定載重;式(21)表示任意一輛車的服務客戶集合不出現閉環;式(22)表示兩個決策變量之間的關系;式(23)表示車場之間不允許通車;式(24)和式(25)為決策變量取值約束。
2 模型求解
2.1 求解思路
首先,利用擴展啟發式算法產生初始可行解,在傳統蟻群遺傳算法的基礎上,引入兩邊逐次修正算法對精英群體進行局部優化。然后,利用定點交叉算法對精英種群進行交叉變異,使之達到初始種群規模。最后,利用正交試驗設計思想,對算法參數進行優化,以最大迭代次數作為算法終止條件。對模型進行求解算法流程見圖4。
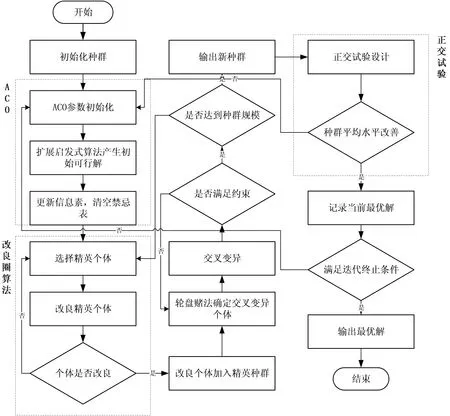
圖4 算法流程
2.2 算法初始化
2.2.1 編碼與解碼
1)編碼
筆者采用十進制編碼,根據車輛和車輛服務的顧客順序進行多段編碼。車輛采用三位數編碼,百位數用于防止與客戶編號重復,十位數表示車場編號。個位數表示車型編號,如112表示第一個車場第二個車型。客戶編碼采用十進制編碼,編號表示客戶編號,見圖5。
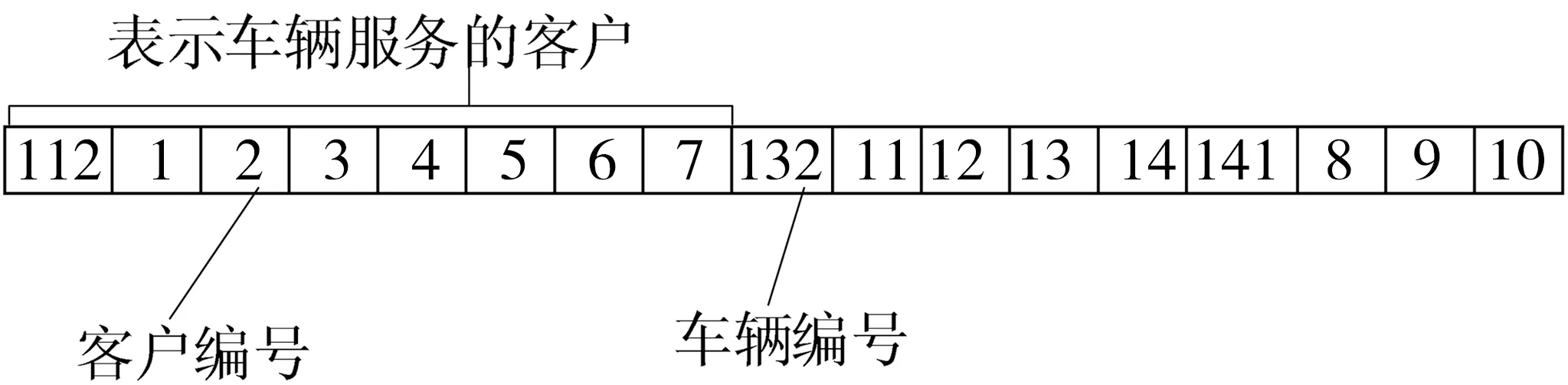
圖5 路徑編碼
2)解碼
根據編碼順序,結合車輛、客戶數據信息,計算該路徑長度、客戶滿意度、使用車輛數,進而計算該路徑的加權目標值。
2.2.2 初始可行解
Step 1隨機選擇服務客戶的車輛,轉Step 2。
Step 2當客戶集不為空集的時候,計算各個未訪問客戶的狀態轉移概率。采用輪盤賭法選擇待服務客戶,轉Step 3;否則,轉Step 4。
Step 3判斷該車輛里程是否能夠返回車場及容量是否有剩余,如果可以,轉Step 2;否則,轉Step 1。
Step 4輸出路徑,計算顧客平均滿意度、車輛數、路徑長度,計算整體目標值。
2.3 改進蟻群-遺傳算法
Step 1設置算法初始參數,導入客戶、車場數據,基于啟發式算法產生初始可行解,詳見2.2.2節,轉Step 2。
Step 2求解本代可行解目標值,若NC>2,則R(1)=R_best(NC-1),其中,R_best(NC-1)為NC-1代最優解;否則,轉Step 3。
Step 3記錄本次迭代最優解,更新信息素,清空禁忌表,轉Step 4。
Step 4對該代個體目標值進行降序排列,選擇前10%作為精英個體,轉Step 5。
Step 5基于輪盤賭法隨機選擇精英個體,利用兩邊逐次修正算法進行改良,見2.4.1節,轉Step 6。
Step 6把改良個體加入精英種群,判斷種群是否達到初始種群規模,是則轉Step 7;否則轉Step 5。
Step 7基于輪盤賭法判斷個體是否需要交叉變異,是則基于定點交叉算法對個體進行交叉變異,詳見2.4.2節,轉Step 8。
Step 8基于輪盤賭法,選擇正交試驗參數,詳見2.4.3節,對交叉變異后的精英種群目標值進行計算,求其平均值,轉Step 9。
Step 9判斷種群平均水平是否得到改善,是則轉Step 10;否則轉Step 8。
Step 10記錄當代種群最優解,判斷是否滿足迭代終止條件,是則轉Step 11;否則轉Step 2。
Step 11輸出最優解。
2.4 局部優化算法
2.4.1 兩邊逐次修正算法
Step 1輸入需要改良的路徑R。
Step 2按服務順序選擇潛在改良點,翻轉改良點之間路徑,即R(i+1:j)=R(j:-1:I,i+1)。記新路徑為R1,判斷改良點是否均被遍歷,是則轉Step 7;否則轉Step 3。
Step 3判斷改良點i與j或改良點i+1和j+1是否皆為車輛,是則令i=i+1,轉Step 2;否則轉Step 4。
Step 4計算R1各車輛行程和荷載,轉Step 5。
Step 5判斷路徑R1中行程或荷載是否存在超出額定值的車輛,若存在,令i=i+1,轉Step 2;否則轉Step 6。
Step 6計算R、R1路徑長度、客戶平均滿意度,分別記為len、len1、S、S1;若len>len1且S Step 7輸出改良的個體R1。 2.4.2 定點交叉算法 路徑R1經過多點、不定點交叉或不定點變異后,易產生未服務客戶或里程、容量超過額定值的車輛。筆者提出定點交叉算法,使得路徑交叉、變異后仍為可行解,步驟如下: Step 1從種群中隨機選擇兩個個體,記為R1、R2,轉Step 2。 Step 2從R1、R2中隨機選擇兩個基因,分別記為a、b,轉Step 3。 Step 3利用find(a=R2(1,:))、find(b=R1(1,:))函數,分別找到a在R2中的位置、b在R1中的位置,分別用p1、p2記錄基因在路徑中的位置,轉Step 4。 Step 4算法隨機把p1、p2位置的基因對應調換在R1、R2其他位置(非首位),產生的新路徑分別記為R_new1、R_new2,轉Step 5。 Step 5計算R_new1、R_new2各個車輛的里程及荷載,轉Step 6。 Step 6判斷R_new1或R_new2中是否存在超出額定荷載和最大行程的車輛,若存在,轉Step 4;否則,轉Step 7。 Step 7輸出R_new1、R_new2。 2.4.3 正交參數設計 對改良蟻群-遺傳混合算法的5個關鍵參數設計L25(56)正交表,每組參數的初始績效值Ni=1,各組參數的選擇概率由式(21)確定: (21) Step 1利用輪盤賭法選擇一組參數應用于當次迭代,轉Step 2。 Step 2判斷種群平均水平是否得到改善,且該組參數的績效值增加1,是則轉Step 3;否則轉Step 1。 Step 3記錄當前最優參數組合及種群最優解。 某生鮮企業在該區域有5個配送中心,每個中心有多種車型,對該區域25個客戶進行配送。每個客戶存在一個模糊預約時間,客戶所定商品具有一定的保鮮期。配送速度受時間和空間的影響,但不能超過最大限速。求得合適的客戶服務順序,使得總目標值最低。 3.2.1車場車型數據 調整Solomon標準算例R101、R201、C101、C201、RC101、RC201,刪除算例中車場,額外增加5個車場。每個車場存在多種車型,車場車型數據見表1、表2。 表1 車場信息 表2 車型信息 3.2.2 客戶位置、時間窗數據 在Solomon算例中客戶時間窗基礎上,向兩側隨機擴展成模糊時間窗,并隨機生成商品最后交貨期。取交集形成綜合模糊時間窗,用x、y表示坐標,C表示客戶需求,l、L、U、u分別表示客戶模糊時間窗上下限,ts表示客戶服務時間,G表示商品保鮮期。部分客戶數據見表3。 表3 客戶數據信息 3.2.3 速度時空參數 設ρ=2,α=0.5,β=0.5,tm取各算例車場運營時間中點,dr0為距離車場中心距離最遠的客戶到車場中心的距離。 3.2.4 正交試驗參數 選擇6個參數,參數水平見表4。設計L25(56)正交表,部分見表5。其中,M、δ、μ、ε、Pc、Pm分別表示螞蟻數、信息素啟發式因子、期望啟發因子、信息素蒸發因子、交叉率、變異率。 表4 正交試驗參數水平 表5 正交試驗表 3.2.5 算法運行環境 算法運行環境為CPU2.20 GHz,內存為4.00 GB,操作系統為64位Windows10,編程語言采用MATLAB R2016a。 表6 不同模型計算結果對比 設其他條件不變,對不同類型的時間窗展開討論,可見對不同分布特征下的客戶,不同類型時間窗車輛配送距離和車輛使用數量差別不大,IFTW模型相比FTW和GTW模型的客戶平均滿意度較高。 因此,綜合考慮路網擁堵特征、客戶時間窗、商品保鮮期的生鮮配送模型可以有效平衡配送時效性和配送時間窗不確定性的矛盾。 為測試結合蟻群算法、遺傳算法、兩邊逐次修正算法提出的改進蟻群-遺傳算法的有效性。將改進算法的各部分分別對不同分布特征的客戶群進行求解,并與改進算法求解結果進行對比。即用改進蟻群-遺傳算法(IACGHA)中的蟻群算法(ACO)模塊、嵌入兩邊逐次修正算法的改進遺傳算法(IGA)模塊、去除兩邊逐次修正算法的遺傳算法(GA)模塊分別對不同分布特征的客戶群進行求解,將求解結果分別與改進蟻群-遺傳算法(ACO-GA)的求解結果進行對比,以檢驗ACO-GA算法的求解能力,對比結果見表7。ACO算法的螞蟻數M=50,信息素啟發因子β=2.5,期望啟發因子μ=4.5,信息素會發因子ε=0.4,信息素強度Q=100。GA和IGA除嵌入兩邊逐次修正算法的差異外,其他參數相同。其中,種群規模NP=100,交叉率Pc=0.7,變異率Pm=0.006,算法迭代次數G=500。 表7 不同算法改進百分比對比 由表7可知,雖然針對部分數據,改進蟻群-遺傳算法計算結果不如傳統算法,但整體上ACO-GA算法計算能力優于傳統算法,平均優化5%以上。由此可見,改進蟻群-遺傳算法相比于傳統算法,計算能力更強,優化效果更好。然而因算法中嵌套正交試驗設計等局部優化模塊,使得算法以最大迭代次數作為迭代終止條件時,計算時間較長。 為解決生鮮配送時效性和配送時間不確定的矛盾及應對生鮮配送多配送中心化的趨勢,筆者綜合考慮客戶時間窗、商品保鮮期、配送速度的時空特點,建立起綜合模糊時間窗和速度的時空函數,以反映生鮮配送過程中的時間不確定性;建立多車場多車型生鮮配送路徑優化模型,以反映生鮮配送多配送中心化的特點。采用不同類型的Solomon算例反映不同分布情況的客戶特點。考慮到在時變路網下考慮時間窗的多車場多車型車輛路徑優化模型較為復雜,提出在傳統蟻群-遺傳算法的基礎上,嵌入兩邊逐次修正算法、正交實驗設計等局部優化模塊的改進蟻群-遺傳算法,對該問題進行求解。 結果表明,考慮多配送中心的綜合模糊時間窗和速度時空演變函數的生鮮配送模型更符合實際,可有效緩解配送時效性和配送時間不確定性之間的矛盾,且改進蟻群-遺傳算法相對傳統算法求解效率更高。文中模型和算法可為生鮮配送企業制定調度計劃提供參考。3 算例分析
3.1 算例描述
3.2 算例說明
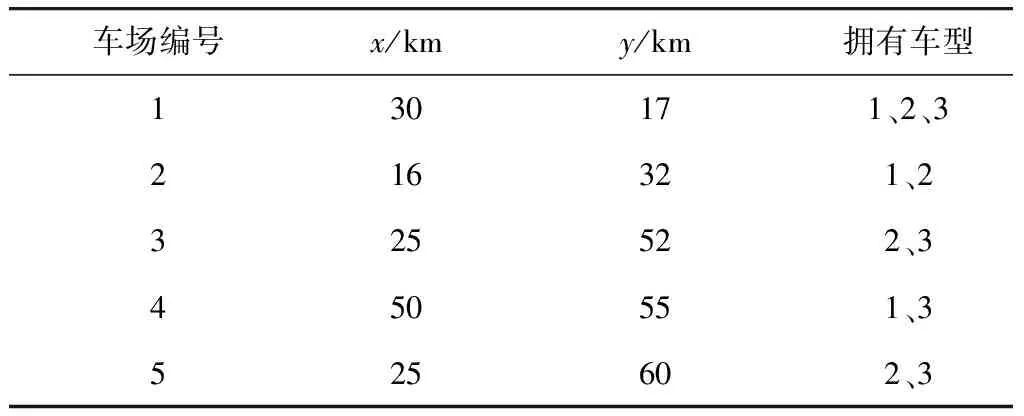
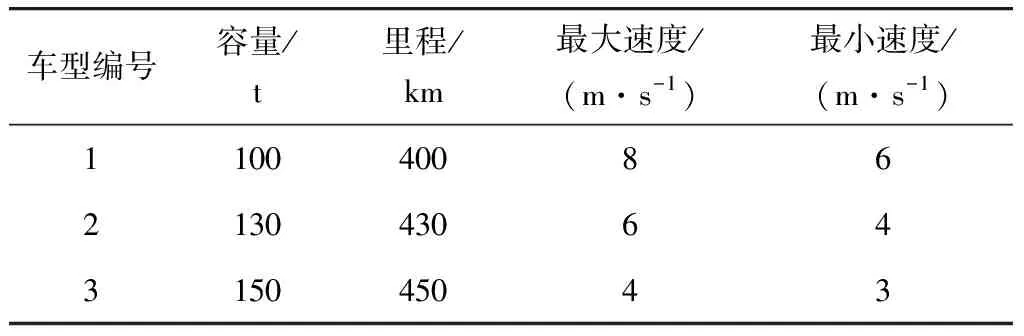
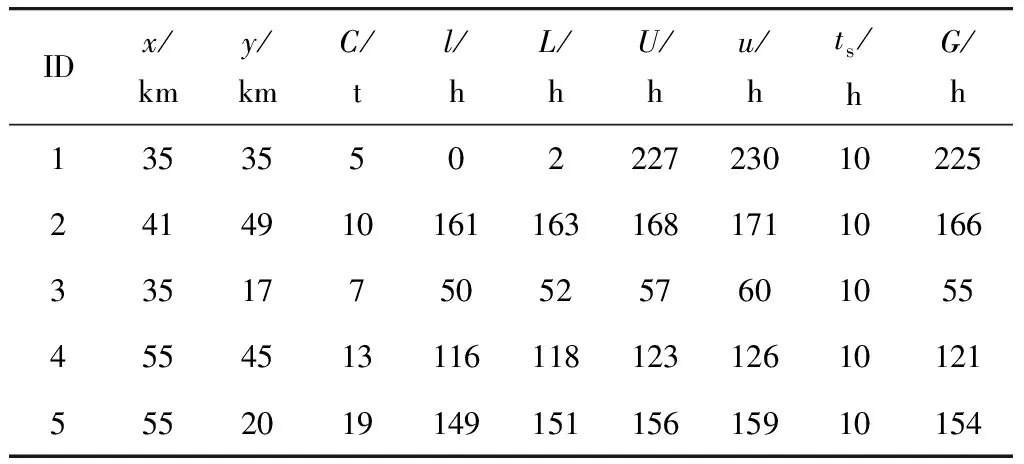
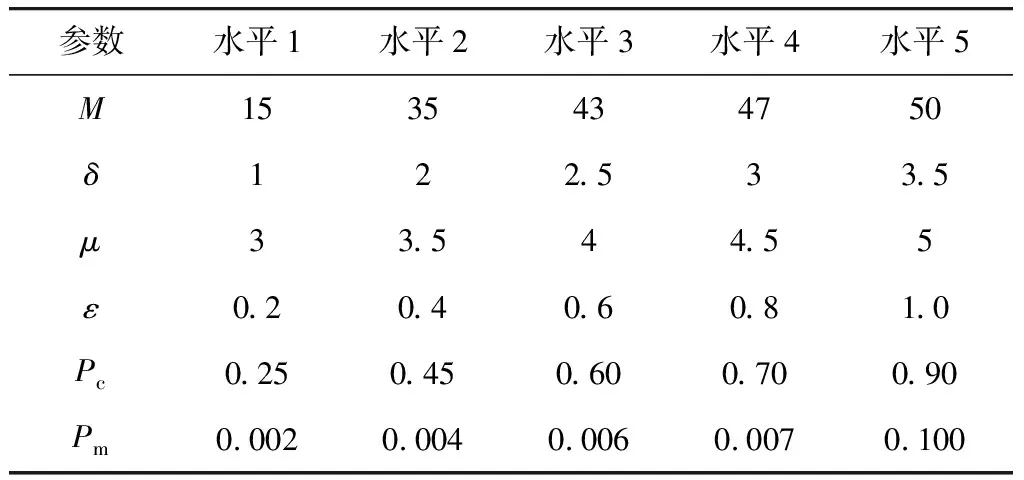
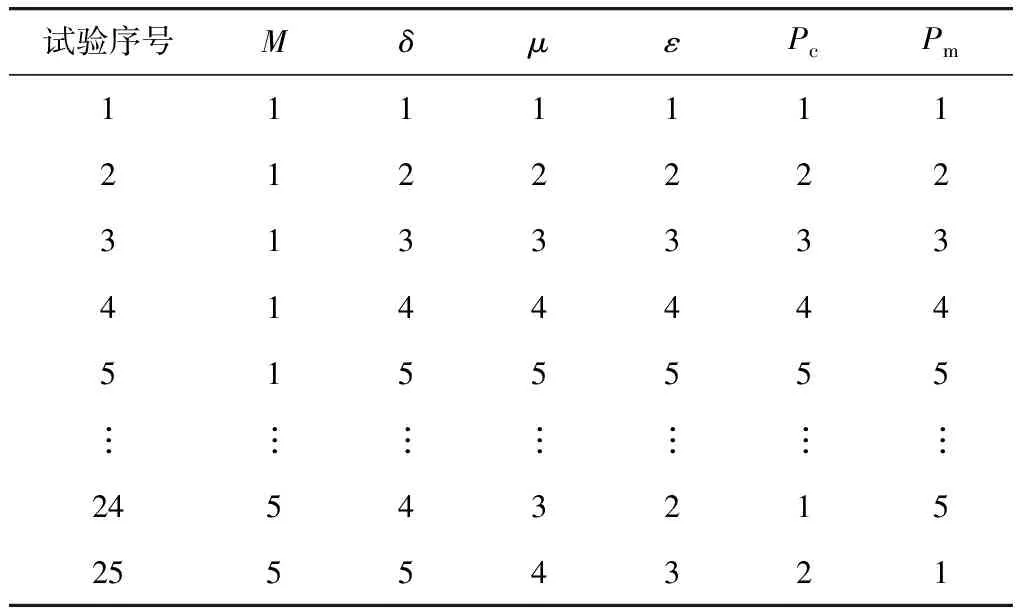
3.3 不同模型相同算法比較結果
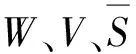
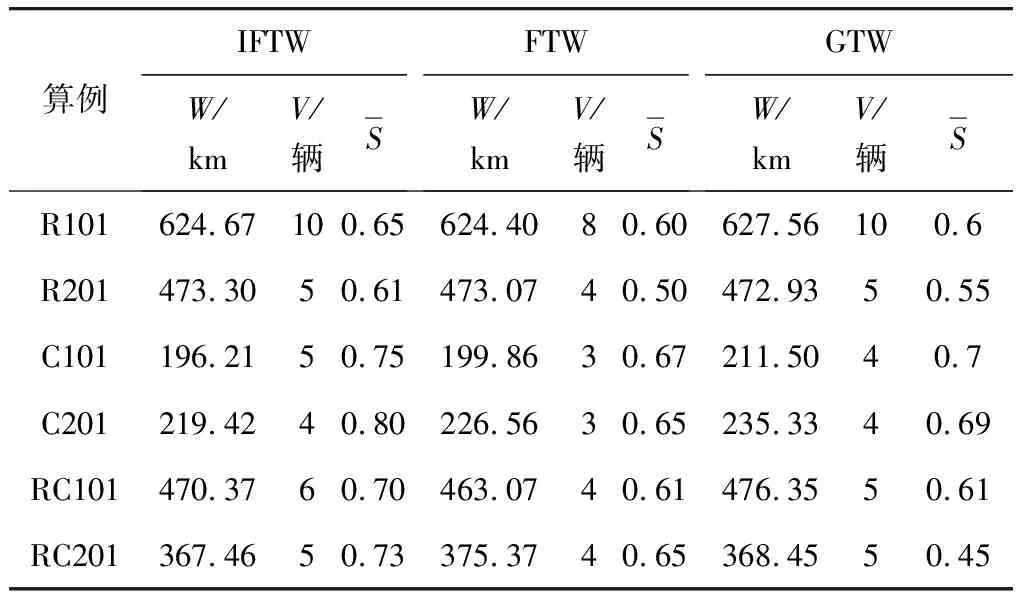
3.4 相同模型不同算法比較結果
4 結 語

