面向目標識別的特征聚類與選擇方法研究

桂洪冠，位凱

（1.達而觀信息科技（上海）有限公司，上海 201203；2.上海海事大學，上海 200135）

0 引 言

目標識別在智能駕駛、智慧交通、智慧安防等多個領域有廣泛的應用，是實現系統智能決策的重要基礎。為了進一步準確地識別目標，需要使用標注數據預先訓練一個分類模型。在識別模型訓練過程中，需要對大量的識別目標進行特征選擇，所選特征的數量及其重要程度直接影響到分類準確率，進而影響目標識別的識別效果。現有的特征聚類算法以聯合非負矩陣分解(Joint Nonnegative Matrix Factorization,JNMF)為主，該算法對噪聲較為敏感。聯合稀疏典型相關分析(Joint Sparse Canonical Correlation Analysis,JSCCA)是一種具有代表性的特征選擇算法，但JSCCA 及其改進算法大多為無監督方法，無法在不同組別之間同時執行并尋找組別之間的特征差異。

本文提出一種未知目標與已有知識圖譜中的目標之間的高效特征關聯與選擇的方法，旨在提高目標識別模型的分類準確率。首先基于JCB-SNMF（Joint Connectivity-based Sparse Nonnegative Matrix Factorization,JCB-SNMF）模型將兩個數據集中的顯著特征聚類，再將選出的特征放入MTSCCALR（Multi Task-Sparse Canonical Correlation Analysis Linear Regression,MT-SCCALR）模型進行特征關聯分析。在模擬數據集的實驗表明，該方法可以有效解決目標識別領域訓練數據集特征冗余以及分類準確率低下的技術問題。

1 現狀

現有的特征聚類算法以聯合非負矩陣分解(Joint Nonnegative Matrix Factorization,JNMF)為主，JNMF 算法通過將不同模態數據的矩陣進行拼接，然后再進行分解來達到降維的目的。降維后得到的基矩陣存放樣本信息，系數矩陣存放特征信息。對于特征共表達模塊的選擇，一般對系數矩陣的每一行采用z-score 標準化后與人為設定的閾值進行比較，當標準值大于閾值，則認為該特征有資格進入到該模塊。在JNMF 基礎上，將先驗知識加入能夠有效提高模型的特征關聯分析性能。但是，大多數改進算法對數據中存在的噪聲較為敏感，在噪聲較大的情況下無法正確選擇重要特征。聯合稀疏典型相關分析(Joint Sparse Canonical Correlation Analysis,JSCCA)是一種具有代表性的特征選擇算法。JSCCA 通過得到兩種數據特征之間最大相關性的線性組合挖掘更顯著的特征。在JSCCA 基礎上，也可加入各種先驗知識以增強數據之間的相關性。但是JSCCA 及其改進算法大多為無監督方法，無法在不同組別之間同時執行并尋找組別之間的特征差異。

當前技術的特征關聯分析與選擇方法還存在準確率和召回率不高的問題，尚無法達到實際應用的需要。如何高效利用已有的知識圖譜中的目標數據集信息進行有效的特征聚類與選擇，進而訓練出準確率高、召回率高的識別模型，目前尚未提出有效的技術方案。

2 方法

本文提出的面向目標識別的知識圖譜輔助特征聚類與選擇方法包括兩部分，第一部分提出一種JCB-SNMF 的特征聚類方法，該方法能夠將目標識別的訓練數據集和對應的知識圖譜中的目標特征投影到同一個公共特征空間，通過這種方法可以實現將顯著特征聚類到顯著共表達模塊。第二部分提出一種MT-SCCALR 的特征關聯與選擇方法，該方法能夠將第一部分篩選出的訓練數據集和目標數據集顯著特征進行關聯分析，進而按需求選出其中的Top 特征用于后續分類。方法過程如圖1所示。

圖1 特征聚類與選擇過程

2.1 特征聚類方法

2.1.1 特征預處理

訓練數據樣本集指在目標識別之前預先訓練的已有標注的樣本，根據標注信息，可在知識圖譜中找到與其對應的目標類型和全部特征信息。根據訓練數據的標注信息對訓練數據按標注類型排序，對應于訓練數據的特征（如飛行目標的速度、高度、航向角等），形成一個每行為一個樣本，每一列為一個樣本特征的數值矩陣。

2.1.2 JCB-SNMF 特征聚類算法

JCB-SNMF 算法是在JSNMF(JointSparseNonnegative Matrix Factorization,JSNMF)算法的基礎上進行的改進。具體為：

NMF 是傳統的降維方法，其一般模型為：

其中，和分別是原始特征矩陣經分解得到的基矩陣和系數矩陣，且的維度是行列，的維度是行列，的維度是行列。、和分別代表樣本數、特征數和降維數。JNMF 算法在NMF 算法的基礎上擴展了輸入數據的種類，即可對多個不同模態數據的特征矩陣同時進行分解，其目標函數為：

X∈R（=1，2，…）代表不同數據的特征矩陣，行數相同，列數不同。∈R代表分解后的公共基矩陣。H∈R代表分解后的對應于原始矩陣的多個具有很強獨立性的系數矩陣，實際使用中＜＜，有學者提出了JSNMNMF，文中為了改善數據之間關聯較弱，假設為相互作用鄰接矩陣，JSMNMNMF 采用了范數和范數分別控制和H的稀疏性以實現數據的稀疏化。因此，其目標函數為：

、、分別代表鄰接矩陣的權重，用于控制的稀疏度，用于控制H的稀疏度。

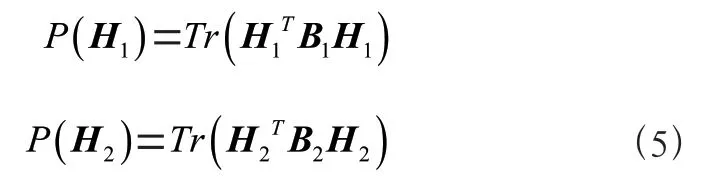
、分別代表、的拉普拉斯矩陣。給出所提出算法的目標函數為：

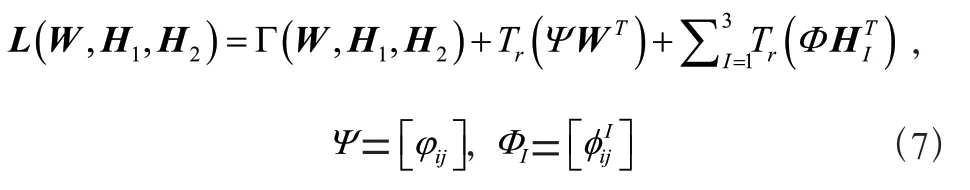
關于和H的偏導為：

根據式(9)的迭代規則，最終將和分解成基矩陣和系數矩陣、。為了找到的每一行的顯著特征對應的權重值，使用z-score 來提取H矩陣每一行的系數。它的定義為：

其中h代表H中的元素，μ代表中H特征的平均值，σ代表標準差。為了確定模塊成員資格，須人為設置一個閾值，如果它的z-score 值比給定的閾值大，則有資格分配到模塊。

接下來，評估每個模塊的顯著性。具體來說，假設A=[，，…，]、B=[，，…，]。其中，a、b分別是從、中選出的列向量。然后，使用式(9)計算同一模塊中元素的平均關聯性。

在本專利中，、分別代表訓練數據和知識圖譜中對應的目標樣本集，根據實際樣本數量和特征數量確定模塊數，一般＜＜。通過式(8)隨機初始化、、，通過多次迭代，使其收斂到一個局部最小值。進而得到公共基矩陣，以及分別對應于、的系數矩陣、。然后根據式（9）計算同一模塊中元素的平均關聯性。最后根據式(10)、式(11)對所有模塊進行顯著性分析，篩選得到最顯著的模塊，模塊中包含兩個數據集的顯著特征用于后續分析。

2.2 知識圖譜輔助特征關聯分析方法

將2.1 章節所述的不在模塊中的特征剔除，保留兩個矩陣在模塊中的特征。將訓練數據標簽和兩個矩陣拼接放入MT-SCCALR 模型，該模型同時執行多個不同類型目標的任務，對于每種目標類型都會求出其每個特征的權重向量，對取絕對值后，按權重從大到小排列。根據需要取每一種目標的Top 特征用于后續分類器分類。具體有以下4 個步驟：

（1）將訓練數據樣本集和與其對應的知識圖譜中的目標樣本集一一對應。其中，根據訓練數據樣本集標注的信息，可在知識圖譜中找到與其對應的目標類型和全部特征信息。進而，分別得到訓練樣本集和知識圖譜的特征矩陣（行為樣本，列為特征），其行數相同，列數不同。兩個矩陣中樣本應是一一對應的。

（2）使用JCB-SNMF 模型將兩個數據集中的顯著特征聚類。

（3）將選出特征放入MT-SCCALR 模型進行特征關聯分析。MT-SCCALR 模型是在傳統的基于SCCA的無監督方法基礎上實現的改進。

CCA算法是一種確定兩個數據集之間關聯的算法。給定數據集∈R和∈R，其中有個特征，有個特征，共個樣本。該算法能夠找到和最大相關性的線性組合。

其中，假定和的列已經標準化，和是和對應的標準化后的特征權重。

SCCA 模型是在CCA 的基礎上加入了懲罰項，用于控制模型的稀疏性，SCCA 模型定義為：

MT-SCCA是一種新穎的模型，它在SCCA 上加入了多任務框架。創新性的在其基礎上加入線性回歸模型，這使得不同目標的類型標簽可以加入。使用來表示目標的種類。分別使用∈R和∈R表示經JCB-SNMF 算法篩選得到的訓練數據集中的目標特征和對應的知識圖譜中的目標特征。∈R是X的權重矩陣，∈R是Y的權重矩陣。

其中，L和L分別代表和的拉普拉斯矩陣，可將其改寫為：

然后在模型中引入線性回歸，其目標函數為：

z代表第個任務的第個標簽。現在可以給出加入線性回歸的模型的目標函數：

然后，得到MT-SCCALR 算法的目標函數，如式(19)所示：

其中，、、、、以及是需要調整的超參數，、、和用于控制模型的稀疏度。刪除常量后，得到式(20)：

為了最小化目標函數（20）以獲得最優的和算法，使用交替凸搜索方法。首先，初始化和，然后，當固定時，修改，反之亦然。并重復上述過程直至收斂。

首先得到一個的值，當是常數時它被最小化。由于拉普拉斯矩陣是正定矩陣，基于連通性的懲罰是凸的，可以使用基于軟閾值的坐標進行優化，因此（20）的坐標解定義為：

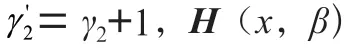
在得到之后，開始對求偏導，的目標函數如式（22）：

用這種方式，可以迭代得到權重的值，如式(24)：

（4）得到訓練樣本集各特征權重，取絕對值后按需要保留Top 特征。將步驟（3）中得到的權重向量u拼接，得到權重矩陣，對取絕對值，其中中列中的每個元素對應于矩陣的每個特征。將每一列從大到小排序。然后根據需要找到Top 特征，用于后續分類等。

3 實驗分析

3.1 數據集預處理

對于原始訓練數據集，需要經范數歸一化，目的在于：

統一數據單位：可以將有單位的數據轉為無單位的標準數據，在目標識別場景下，訓練數據集和知識圖譜中已有目標的各種參數可能使用了不同單位，將這些數據經過歸一化統一都映射到（0，1）這個區間,這樣能夠保證所有數據的取值范圍都在同一個區間里的。

此外，歸一化可有效避免模型梯度求導計算時在垂直等高線的方向上走大量無畏的之字形路線，從而減小迭代計算量和迭代次數，加快模型收斂速度。

對應知識圖譜中的數據集，在知識圖譜中依據訓練數據標簽找出對應的目標全部特征，然后同樣進行范數歸一化處理。得到與訓練樣本集行數（樣本）相同、列數（樣本特征）不同的數值矩陣。

3.2 模型參數選取

將預處理好的訓練樣本數值矩陣和與其對應的知識圖譜中的數據放入JCB-SNMF 模型中，調整模型參數、、、、。對于模塊數的選取，需要固定其他參數，然后將逐漸增大，在保證＜＜的情況下，比較不同值下的目標函數值，選取目標函數值最小的作為模塊數。此外，固定以上參數后，隨機初始化100 組、、的參數組合后，計算100 組參數組合下的目標函數值，選取最小的目標函數值對應的參數組合。最后利用式（8）迭代更新使得模型收斂到局部最小值。

3.3 特征聚類

根據式(10)(11)可以計算出個共表達模塊的顯著性值，選取最顯著的模塊(＜0.01)。提取最顯著的共表達模塊中包含的特征，更新矩陣和，使用該模塊中和的特征，將其余特征刪除，進而更新矩陣和。

3.4 特征關聯分析與選擇

將處理好的、放入MT-SCCALR 模型，調整模型中的、、、、以及。具體調整方法為：

由于盲網格搜索十分的耗時，采用了一些相關方法來加速調整參數的過程。一方面，如果參數太小了，SCCA 和CCA 會產生相似的結果。另一方面，如果參數過大，SCCA將過度懲罰結果。因此，參數的選取不宜過大或者過小。用五折交叉驗證的方法來尋找最優參數。使得測試集結果的相關系數最高的參數組合將被定為最優參數。公式如下。

根據式（21）（24）可以得到每種目標在訓練集和知識圖譜中的權重向量u和v。將得到的每一個權重向量u取絕對值，然后按從大到小的順序排列，按實際需要選取其中Top 特征，用于后續分類等。

4 結 論

本文提出了一種組合特征關聯與選擇方法，該方法通過JCB-SNMF 算法進行特征聚類和關聯，通過MT-SCCALR方法進行特征選擇，獲得了更高的準確率。為目標的準確檢測提供新見解。然而，該方法也存在一些不足。如基于SCCA 的方法具有較高的時間復雜度，對于較高維的數據特征關聯分析較為困難。因此，在未來的研究中，需要對MTSCCALR 算法的目標函數求解進行進一步優化，降低時間復雜度。此外，我們也將嘗試使用更多的數據集進行方法有效性驗證。